计及供给侧出力的数据挖掘负荷预测方法
刘庆彪, 张桂红, 许德操, 秦绪武, 白左霞
(青海省电力公司经济技术研究院 发展部, 西宁 810008)
电力系统作为一个集发、输、变、配及用电于一体的大规模复杂能源供应网络,电能的生产和使用都具有较为明显的即时性[1].为保证电力系统经济高效且稳定地运行,需要保持电能生产和消费环节的平衡.合理、准确的负荷预测是保证电能产销平衡的关键[2-3].电力系统负荷预测是能量管理系统的重要组成部分,是在了解系统运行特性、负荷本身等规律的基础上,通过历史数据对未来负荷发展变化进行的可靠预测[4-6].
现有负荷预测方法主要有:时间序列法、灰色预测法、神经网络组合预测法等[7].负荷具有非线性及周期性,时间序列法、灰色预测法等方法均难以适用[8].虽然相比于传统方法,聚类分析与神经网络预测法在预测精度上有所提升,但对于非周期性的负荷预测效果仍有待提升[9].
新能源形势要求更深入分析用能特性与规律,做到负荷的精准预测,提升负荷预测的效率和精度[10].因此,本文提出了一种计及供给侧出力的数据负荷预测方法,在充分考虑供给侧出力的基础上设计净负荷的理念,深度挖掘发电、用电与气象因素的关联,利用支持向量机(SVM)对负荷进行准确预测.
1 数据挖掘
数据挖掘是采用模式识别、数学统计等方法,从大量数据中挖掘出可能有潜在价值的信息技术,并实现分类、聚类、关联和预测功能[11-12].根据数据挖掘的基本概念和功能,本文结合K-means聚类分析和灰色关联技术,设计了一种具有分类和关联功能的数据挖掘技术.
1.1 聚类分析
K-means算法作为一类动态的聚类技术,其评估相似度的方式是统计两个对象之间的欧氏距离,距离越近则说明相似程度越高.K-means算法的聚类过程如下:
1) 从给定的具有n个k维数据的集合X={x1,x2,…,xi,…,xn},xi∈Rk中选取Q个点当作开始聚类的核心,任一对象均可表示一个类型的中心φq(q=1,2,…,Q).
2) 统计各个点到中心φq间的欧氏距离,然后根据其远近,将各数据点划分到最相近的聚类中心内,所有数据点到聚类中心φq的距离平方和J(cq)可表示为
(1)
3) 计算所有样本的J(cq),以得到总体距离平方和J(C).当J(C)达到最小时,将该类内所有对象的均值作为新的聚类中心.
4) 判定聚类中心与J(C)值有无发生变化,若发生变化,则转到步骤2);若无发生变化,则聚类过程终止.
采用K-means算法对历史数据集内的温度、湿度、风速等气象条件进行聚类,同一类型内的气象数据特征是接近的,同一类型的相似性越大,不同类型之间的差别越大,即聚类效果越优.
1.2 灰色关联分析理论
灰色关联分析主要是利用曲线的近似等级来判定相关程度,是一种剖析系统内所有因素相关程度的方式[12].在关联分析中,首先需要构造序列矩阵,通过K-means聚类算法初步分析历史数据,得到与待预测时间段近似的气象历史数据,然后对其进行关联次序的剖析.
假定,T0表示待预测时间段的气象特征,若待预测时间段的气象信息是:最高气温45 ℃,平均气温30 ℃,最低气温25 ℃,雨量20 mm,则T0=(T0(1),T0(2),T0(3),T0(4))=(45,30,25,20).以此类推,采用已经获得的数据集内每天的气象数据构成对比序列,用T1,T2,…,Tn进行表述,则n+1个序列所组成的矩阵描述为
(2)
为了消除量纲,用初值化方法进行数据处理,即
T′i(j)=Ti(j)/Ti(1)
(i=0,1,2,…,n;j=1,2,…,m)
(3)
最终,计算关联系数和关联度为
ρi(j)=
(4)
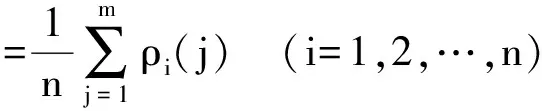
(5)
式中,γ为分辨系数,通常取0.5.
2 计及供给侧的负荷预测方法
由于青海地区赋有充裕的风光水资源,依托这些资源进行发电,能够较优地丰富电力系统供给侧的电源类型.包含风、光、水的发电系统与大电网组合,可看作为大电网末端的变动负荷,需要考虑极端天气等气象因素带来的影响;负荷特性由系统内风、光、水发电量和用户负荷共同决定[13-14].考虑节假日及波峰波谷因素,计及供给侧的负荷预测模型如图1所示.
在传统预测模型中,需要对负荷、风电、光伏、水力分别构建预测模型并进行预测,但对每组数据进行一次建模预测耗时较长.为此提出了净负荷概念,即将新能源发电系统视为带负值的负荷,用户负荷是常规负荷,将两者相加构成净负荷[15-16].由数据采集器获得供给侧与负荷侧的功率数据,上传送至中心服务器进行净负荷运算并利用相应的预测方法实现负荷预测.最终将预测结果传送至对应的机构,为电网调度决策的制定提供一定的参考.
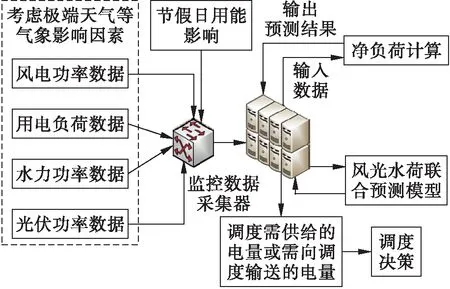
图1 风光水负荷联合预测模型Fig.1 Combined forecasting model for wind,light and water loads
2.1 净负荷
净负荷P′为供给侧出力与用户负荷之和,计算表达式为
P′=PU+(-PPV)+(-PWF)+(-PWA)
(6)
式中:PU为用户负荷;PPV、PWF、PWA分别为光伏、风力和水力的发电量.
若P′<0,则说明供给侧的出力大于用户侧消耗,需要进行储能;若P′>0,则说明供给侧的出力小于用户侧消耗,火力等传统电能需要保证供电;若P′=0,则说明供需处于平衡.
光伏、风力、水力等供给侧出力及用户用电均与温度、湿度、风速等有着紧密的关系.但所提方法考虑的是净负荷整体,因此需要引入影响因子α来表示气象条件对净负荷的干扰.α的计算表达式为
α=aTx-aTy+bTx+cTz+dTy
(7)
式中:Tx为温度数列;Ty为湿度数列;Tz为风速数列;a、b、c、d分别为气象因素对用户负荷、光伏、风力、水力的影响比例.仿真实验将青海省某地级市区域负荷和供给侧作为研究对象,通过查阅气象数据记录,确定分布式能源所处工况,从而确定影响比例参数.
2.2 负荷预测方法
数据挖掘技术在实际应用过程中对噪声比较敏感,因此,其泛化性能较差,而SVM方法能较优地抑制噪声干扰.本文将两者相结合,先用数据挖掘技术对数据进行预处理,以便在建立SVM预测模型时,不需要再次考虑气象因素.然后,按照数据挖掘预处理后得到的数据特征构建负荷预测系统,具体预测流程如图2所示.
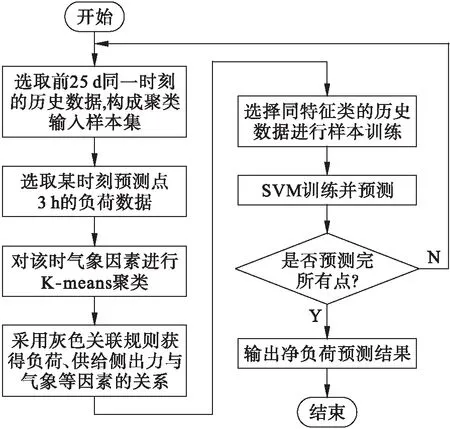
图2 基于数据挖掘的负荷预测流程Fig.2 Flow chart of load forecasting based on data mining
负荷预测主要流程如下:
1) 根据预测相似准则,从预处理后的数据中选出和待预测时间段关联的历史数据,如负荷、供给侧出力等,从而构成待预测时间段的数据挖掘样本集.
2) 采用K-means聚类算法对数据集中的气象因素进行聚类,结合聚类的结果选出和待预测时间段气象条件相同的历史数据集,将其当作训练集.
3) 将数据集中的气象数据与供给侧出力、负荷关系进行灰色关联分析,得到气象数据与发电量关联关系.
4) 对所得的数据集运用SVM算法进行训练并预测.
3 实验结果与分析
利用智能化量测装置采集青海省某地级市2019年1~7月的气象数据,同步采集的还有供给侧、用户侧的电量数据,包括水电、风电、光伏以及用户负荷等,最终构成仿真实验数据集.利用MATLAB搭建仿真模型并对所提方法进行实验,电脑为配置为CPU i7-6500K,DDR 36 GB内存,Windows 10系统.实验参数设置为:γ=0.5,a、b、c、d分别为0.4、0.3、0.2、0.1.
为了评估所提方法的预测性能,采用平均绝对误差(MAPE)、均方根误差(RMSE)、绝对误差(AE)和预测准确度(FA)4个指标进行评价.
3.1 供给侧出力与负荷预测结果分析
利用所提预测方法,对2019年8月22~30日风、光、水及负荷的功率进行预测,通过设定每分钟一次的采样频率分别对风电、光伏、水电以及负荷进行数据收集,同时通过数据拟合,将离散型数据近似地转换为连续的出力曲线,预测值与真实值对比结果如图3所示.
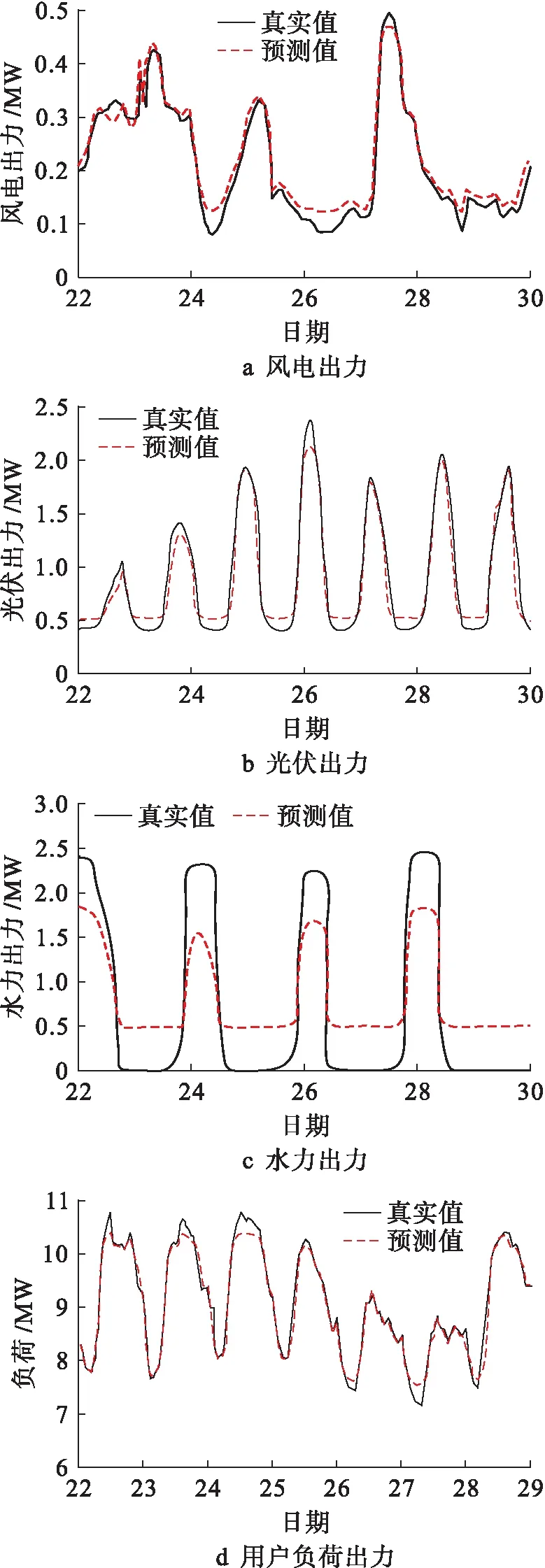
图3 供给侧出力与负荷预测结果Fig.3 Supply side output and load forecasting results
由图3可以看出,无论是供给侧出力或是负荷侧,预测结果与实际值均相差较小.由于光伏与日照的关联较大,出力曲线成近似锯齿状;水力发电受蓄水时间影响,发电在短时间内完成,因此出力曲线近似柱状且预测结果偏差稍大.根据供给侧与负荷侧的电力数据,可得到净负荷的预测结果如图4所示.
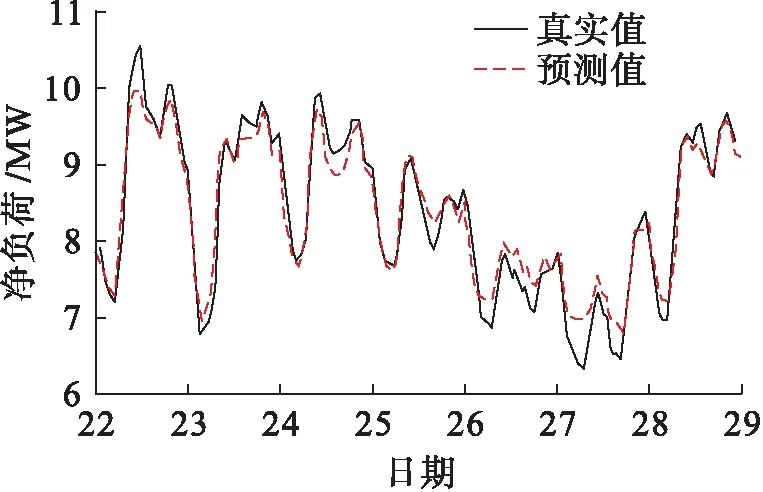
图4 净负荷出力预测Fig.4 Forecasting of net load output
由图4可以看出,净负荷是多方影响的综合结果,与实际值的变化趋势保持一致,且数值相差较小.由于气象因素变化较大,严重影响了用户的电量使用情况,因此部分时间段预测结果与真实值相差较大.但整体而言,净负荷的预测结果是可以满足要求的.
3.2 预测性能对比
结合上述供给侧出力预测数据,利用所提方法对实验区域8月上半月的负荷进行了预测,气象参数为前期分布式电源出力预测时使用的参数,并使用同期该区域历史负荷数据作为训练数据集进行数据分类预测.同时,为了验证所提方法的预测性能,将其与文献[5]、文献[9]和文献[12]的方法进行对比,预测结果如图5所示.

图5 不同方法的预测拟合曲线Fig.5 Forecasting fitting curves of different methods
由图5可以看出,相比于其他方法,所提方法的拟合曲线最接近真实值.由此可见,所提方法的预测效果较优且精度高,是一种新的实用型方法.文献[5]采用的改进SLIQ算法较为简单,预测结果与真实值相差较大;文献[9]结合奇异谱分析与神经网络进行负荷预测,其预测曲线比文献[5]更接近于真实值,但干扰因素考虑不够,影响了预测结果;文献[12]由于无法与气象等多种因素相适应,因此在后期的预测偏差较大.
为了定量分析所提方法的预测效果,将不同方法的各评价指标汇总如表1所示.
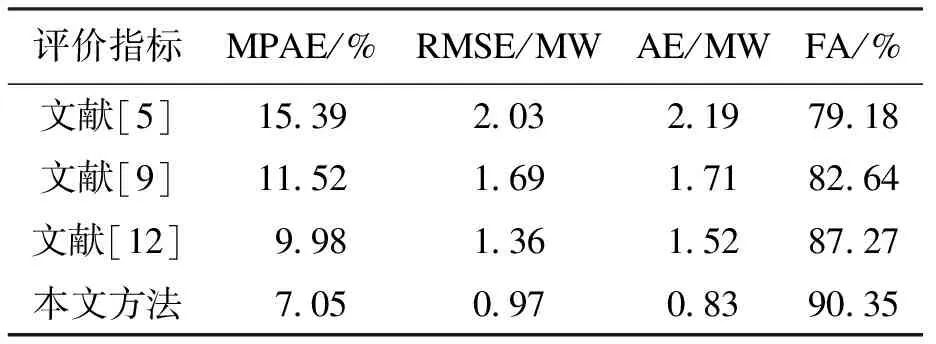
表1 不同方法的预测评价结果Tab.1 Forecasting and evaluation results
从表1中可看出,所提方法的预测性能最佳,MPAE、RMSE、AE和FA分别为7.05%、0.97 MW、0.83 MW和90.35%.由于所提方法采用数据挖掘与SVM相结合的方法,最大程度地挖掘了气象与负荷的关系,得到了更为精准的预测结果.
此外,由于负荷预测需要进行大量的数据处理和分析,预测所需时间也是算法性能的一个重要体现.以8月下旬21~24单日负荷情况为研究对象,将所提方法与文献[5]、文献[9]、文献[12]方法进行对比,预测时间对比结果如图6所示.
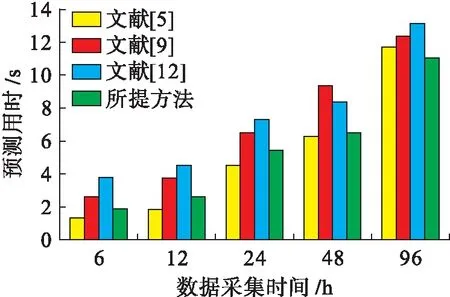
图6 不同方法的预测时间Fig.6 Forecasting time obtained by different methods
由图6可以看出,所提方法的预测时间相对较短,以24 h为例,其预测时间约为5 s.由于文献[5]的算法简单,前期预测时间最短,但随着数据的增加,算法分析能力下降,预测时间超过所提方法,在96 h的预测时间超过了10 s.文献[9]以及文献[12]由于缺乏数据预处理环节,整体数据量较大,耗时都比较长,96 h的预测时间最长超过了12 s.
4 结 论
风电、光伏、水力及负荷的准确预测是电网安全和经济运行的重要前提,为此本文提出了一种计及供给侧出力数据挖掘的负荷预测方法.采用K-means算法和灰色关联分析对样本数据集进行预处理,并提出净负荷概念.将处理后的数据集输入SVM预测模型,实现负荷预测.基于历史数据集和MATLAB平台对所提方法进行实验,结果表明,无论是对风、光、水供给侧的出力预测,还是对用户侧的负荷预测,方法均能得到与真实值较为接近的预测结果,且所提方法的各项指标均优于其他对比方法,具有一定的实用价值.由于所提方法仅考虑了供给侧出力的影响,未考虑用户的用电习惯,因此在接下来的研究中,将重点研究负荷预测中的用户行为,以进一步提高负荷预测的准确度.

