基于投影余角的多普勒雷达几何检测器

梁 璞, 范红旗, 付 强

(1. 国防科技大学电子科学学院ATR重点实验室, 湖南 长沙 410073;2. 中国人民解放军96747部队, 青海 西宁 810007)

0 引 言

信号检测是统计信号处理研究的核心内容之一,广泛应用于雷达、声纳、图像等领域。在雷达信号检测领域,当内部噪声及外部杂波平稳且统计特性完全已知时,可根据纽曼皮尔逊(Neyman-Pearson,NP)准则确定检测器门限。但实际中,雷达目标检测中经常面临动态起伏的非平稳噪声或杂波,且其统计特性通常是先验未知的。针对起伏变化的未知噪声及杂波下的检测问题,雷达领域广泛采用恒虚警率(constant false alarm rate, CFAR)检测器,基于幅度或功率检波,通过对参考单元的动态估计给出自适应变化的门限,从而实现恒定虚警检测。比较常用的恒虚警检测策略包括:单元平均恒虚警(cell averaging-CFAR, CA-CFAR)、选大恒虚警(greatest of-CFAR, GO-CFAR)、选小恒虚警(smallest of-CFAR, SO-CFAR)、有序统计恒虚警(order statistics-CFAR, OS-CFAR),其区别在于参考单元的选择及噪声、杂波电平的估计方法。

但传统CFAR检测器在应用中存在两个固有的缺陷:① 因非理想的背景电平估计而引入的恒虚警损失;② 因包络/功率检波器的线性或平方放大效应而导致的大动态信号和杂波干扰适应能力较差,例如当参考单元内存在强干扰信号(大目标、干扰)或杂波分布不均匀时,恒虚警检测性能急剧下降。GO-CFAR、SO-CFAR、OS-CFAR虽然可在一定程度上改善检测器的适应能力,但额外附加的逻辑和非线性排序等算法增加了计算的复杂性和设计要求,且无法避免恒虚警损失。

几何代数(geometric algebra, GA)是统一代数与几何的一种数学工具,给矢量的代数操作赋予了丰富的几何意义。利用GA工具重新审视矢量的代数操作,有利于从几何直观上构造新的信息处理算子和检测问题的检验统计量,近年来逐渐应用于信号处理、雷达、图像处理和机器人等领域。在信号检测方面,Sangston在最近的一篇综述性论文中基于2-Blade的概念,给出了离散傅里叶变换(discrete Fourier transform, DFT)的几何解释,并定性讨论了其用于信号检测的可能性和优势,但并未结合具体的雷达信号检测问题探讨检测器的设计与性能分析。

本文针对多普勒雷达信号检测应用,提出并推导了内积与GA之间的关系,基于此重新理解检测器的输入信号,并依据几何意义构造不同于幅度和功率检波的几何检验统计量,进而设计新的检测器(本文称之为几何检测器);最后,通过在不同条件下与传统CFAR检测器的性能对比来说明几何检测器的适用性及其优势。

1 几何代数基础

1.1 GA中外积、几何积的定义

考虑中的两个非零且不相关的矢量、,令{,}为这两个矢量所在超平面内的一组正交基,则、可表示为=a+b,=c+d。通常,矢量的内积可定义为

·=+=||||cos

(1)

式中: 是与的夹角;||与||是与的模值。

同时,引入外积的定义:

∧=(-)∧=||||sin ∧

(2)

式中:外积的大小为||||sin ,方向由旋向,如图1所示。

图1 u与v的外积

外积生成的是一个既不同于标量又不同于矢量的新数学实体,对比叉积,后者只定义在三维空间,而外积可扩展到更高维空间。两个不相关矢量的外积称为2-矢量或2-Blade,表示有方向的面,即中的超平面,改变两矢量的先后顺序,所得有向平面的方向也随之变化。同理,也可定义3个甚至多个不相关矢量的外积,称作-矢量或-Blade,例如3-Blade表示中的一个有向体。

在GA中,用零矢量(标量)、矢量、2-矢量和3-矢量分别表示点、有向线段、平面和空间体。当维数大于 3 时,表示-矢量。因此,GA空间内的元素可表示为

(3)

式中：〈〉表示中的-矢量;称为多重矢量(Multivector)。

Clifford将内积与外积结合起来,形成几何积,记为:

=·+∧

(4)

两个矢量的几何积是一个标量与一个2-矢量的组合。这里可从“复数拓展”的角度来看待几何积,正如一个实数和一个纯虚数的和组成了一个复数一样,几何积的表示方法和复数的表示十分相似,在接下来利用GA处理旋转问题时,可更直观地看出这一点。这一表述方式,使得GA拓展了复数的概念。

一般对于中的一组单位正交基{}(=1,2,…,),易得几何积有下述运算性质:

(5)

令=∧,由式(5)可得,通过右乘使矢量逆时针旋转了90°,通过左乘使矢量顺时针旋转了90°,而自乘相当于将标量1逆时针旋转了180°。不难看出,和复数中的非常相似:它也具有自乘为-1,并且在复平面上进行旋转的几何意义。进一步地,可将一个标量和双矢量通过几何积衔接起来,构成一个可视为复数的多重矢量:

=+=+=||ei

(6)

式中：和是实数;是从标量1旋转到的角度。复数可正交分解为复平面上的实轴与虚轴对应的两个分量,对于一个复平面上的1-矢量=+,只需左乘,就可实现其与多重矢量之间的转换:

=+=

(7)

对于一个复数,若要将其逆时针旋转得到′,只需左乘ei即可。假设′与1-矢量′是等价的,利用的指数形式,有

′=′=e =e =e

(8)

可见,利用式(8)可以实现矢量在平面逆时针旋转的几何操作。这一过程可扩展到任意维数。

1.2 复矢量内积的几何含义

首先定义空间与2空间之间的同构映射:∶→2,从而在与2之间建立等价对应关系。

一般地,对于中的复矢量与单位复矢量,可构造下述映射:

=[Re()+iIm()]

(9)

=[Re()+iIm()]

(10)

(11)

(12)

(13)

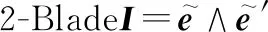
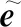
(14)

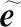
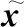
(15)

各个数学量的几何含义如图2所示。

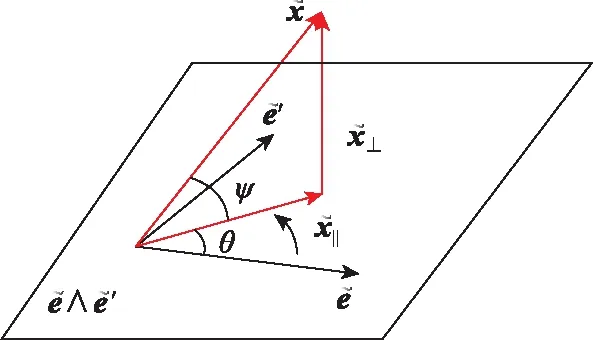
图2 各个数学量的几何含义

基于上述定义,本文提出如下定理:

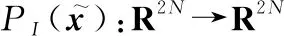
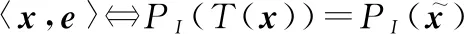
(16)

该定理的代数证明如下:

由式(9)和式(10)及内积的定义可得

〈,〉==
[Re()-iIm()][Re()+iIm()]=
[Re()Re()+Im()Im()]+
i[Re()Im()-Im()Re()]

(17)

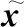
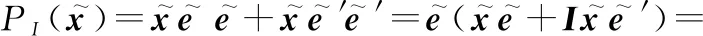
(18)

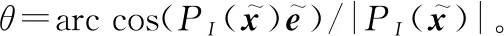
证毕

该定理可广泛应用于相关滤波、信号变换与检测估计问题,为雷达声纳等领域的复信号处理提供了一种新的几何视角。下面来探讨在雷达信号检测中的应用。

2 几何检测器构造

2.1 雷达信号模型

不失一般性,假设某时刻脉冲多普勒雷达任一距离单元内的接收信号可表示为下述离散复正弦形式:

[]=ej( +),=0,1,…,-1

(19)

式中:为信号幅度;为目标的多普勒角频率;为信号初始相位;为采样点数;为采样间隔,一般等于脉冲重复周期。

假设噪声序列为[],则雷达信号检测问题的假设检验可描述为

H∶[]=[],=0,1,…,-1

H∶[]=[]+[],=0,1,…,-1

为了提高输入信噪比,脉冲多普勒雷达通常采用相干积累技术,在现代雷达系统中通常由快速傅里叶变换(fast Fourier transform, FFT)变换来实现。

2.2 DFT的几何解释

DFT的表达式为

=0,1,…,-1

(20)

式中：为观测信号矢量;为第个离散频率对应的单位正交基矢量,即

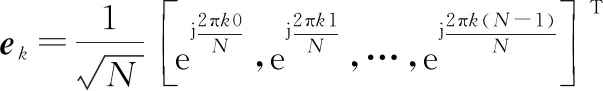
(21)

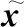
图3 DFT的几何含义

2.3 几何检测器的构造

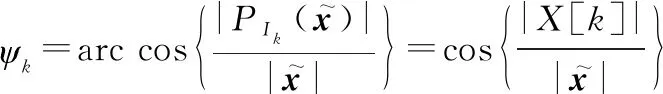
(22)

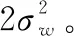
首先考虑当观测信号中不包含频率的信号成分(H条件下),此时易知()服从复高斯分布,其均值和方差分别为

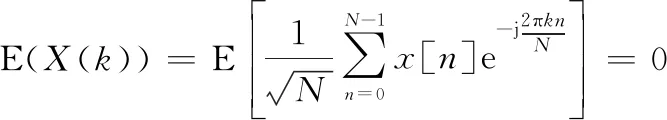
(23)

(24)

则|()|服从瑞利分布,其均值为

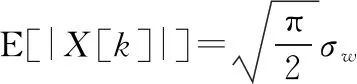
(25)

(26)

由式(26)可得其均值与方差分别为

(27)

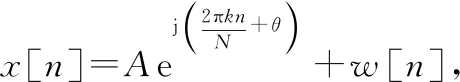
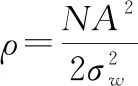
(28)

()仍服从复高斯分布,且

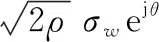
(29)

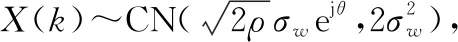
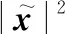
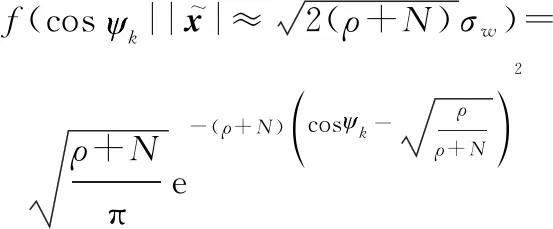
(30)

由式(30)可得其均值与方差为

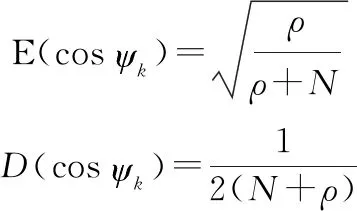
(31)

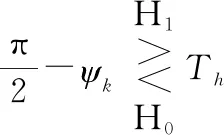
(32)

实际应用中,信号检测流程可描述如下:

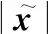
(3) 根据式(32)求取检验统计量并做检测判决。

这里将上述结构的检测器称为几何检测器。它与传统的基于功率包络检波的检测器结构对比如图4所示。

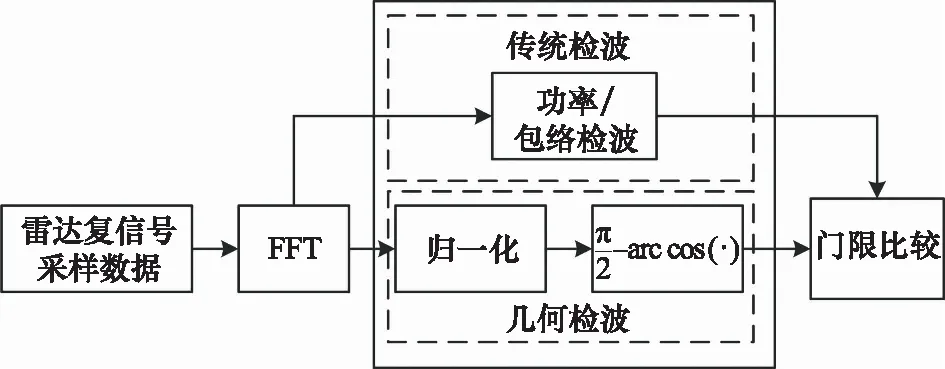
图4 几何检测器与功率/包络检测器结构对比

相对于传统功率包络检波,几何检波的过程增加了归一化及反余弦变换这两个过程。一方面,通过归一化,当噪声或杂波随时间起伏变化时,输出数据可保持相对稳定,从而使检测器具有适应背景起伏的能力;另一方面,反余弦变换是典型的非线性变换,具有良好的动态压缩性质,使检测器具有适应目标信号大动态范围变化的潜力。

根据NP准则及式(26)和式(30),几何检测器的虚警率与检测概率可由以下两式给出:

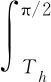
(33)

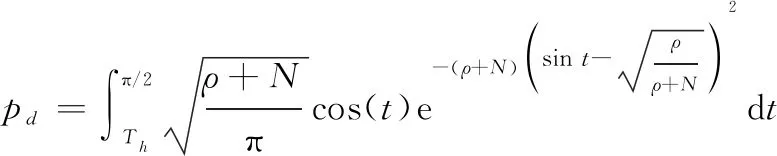
(34)

3 仿真与分析

3.1 仿真说明

本节针对噪声背景起伏、杂波边缘以及双目标干扰等典型检测器场景,通过与传统CFAR检测器的仿真对比说明几何检测器的性能。

多普勒雷达信号检测问题如下:

H:[]=[],=0,1,…,-1
H:[]=[]+[],=0,1,…,-1

式中：[]、[]和[]分别是观测信号[]、实际信号[]及噪声[]经FFT后的输出。

当回波存在杂波时,检测器输入如下:

H:[]=[]+[],=0,1，…,-1
H:[]=[]+[]+[],=0,1,…,-1

式中:[]为杂波[]=ej(+)(=0,1,…,-1)经FFT后的输出。其中,为杂波的幅度,为杂波的多普勒角频率,为杂波初始相位。仿真中假设杂波均匀分布在第64至第96个多普勒单元,即

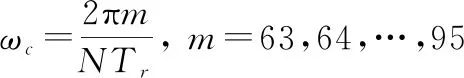
(35)

定义杂噪比为相干积累后的杂噪比,即

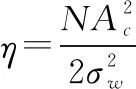
(36)

其余参数及典型值设置如表1所示。

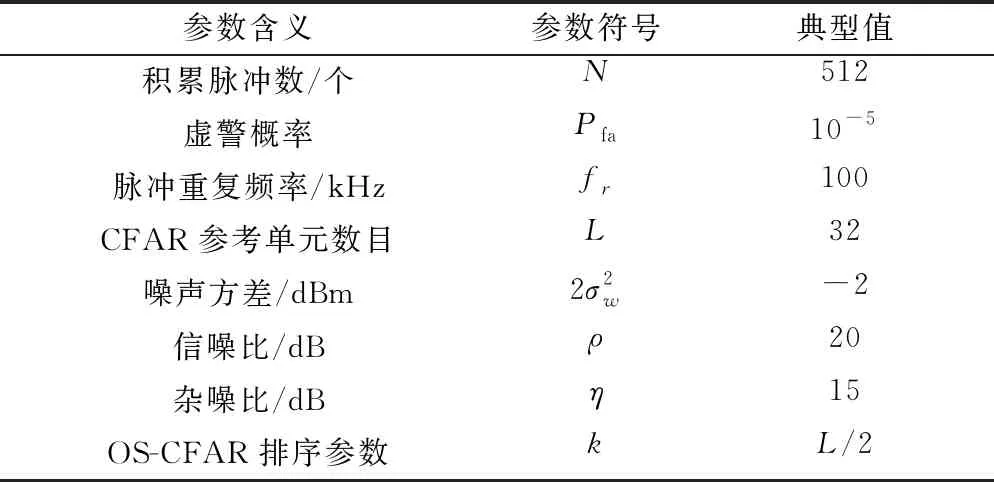
表1 仿真参数设置

3.2 噪声背景起伏

本节讨论噪声均匀起伏时几何检测器的性能。

在实际应用中,起伏噪声的统计特性通常是未知的,相对已知统计特性的最佳检测器,各类恒虚警检测器都存在恒虚警损失。图5对比了均匀噪声背景下最佳检测器、几何检测器与CA-CFAR检测器的检测性能,其中几何检测器的门限可通过计算式(33)中的定积分得出,图中同时给出了几何检测器由蒙特卡罗仿真与依据式(34)分别得到的检测概率曲线。

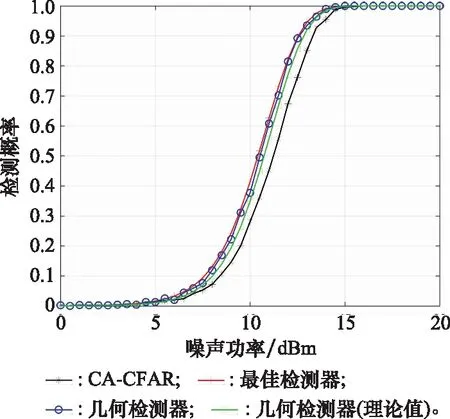
图5 3种检测器检验概率对比图

由图5可以看出,在均匀起伏噪声背景下,针对几何检测器,蒙特卡罗仿真与理论计算所得到的检测概率曲线是一致的,其检测性能接近于最佳检测器,恒虚警损失几乎为零,而CA-CFAR作为均匀背景下的最佳恒虚警检测器,其在0.9检测概率处的恒虚警损失接近0.8 dB。由此可见,均匀起伏噪声背景下,采用几何检测器可有效避免恒虚警损失,提升检测性能。

3.3 杂波边缘检测

在雷达接收回波中,会有杂波干扰的存在,例如海杂波或地杂波。本节考虑杂波边缘附近的目标检测。

仿真中,假设杂波均匀分布在第64至第96个多普勒单元,目标位于第101个多普勒单元,其他参数设置如表1所示。图6给出了CA-CFAR、OS-CFAR、SO-CFAR、GO-CFAR以及几何检测器的门限值。4种CFAR检测器门限分别由参考文献[17]的式(3.8)、式(3.19)、式(3.15)和式(3.16)得到,输出为归一化后的结果。图6只显示了第1到第150个多普勒单元。

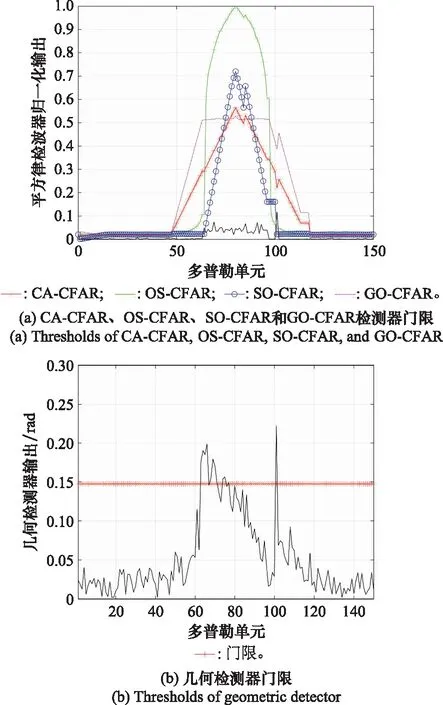
图6 4种CFAR检测器与几何检测器门限

由图6可以看出,当信号处于杂波边缘时,CA-CFAR检测器以及GO-CFAR检测器会因为参考单元落入杂波信号而使门限值抬高,导致信号漏检;SO-CFAR及OS-CFAR均可将信号检测出来;几何检测器由于归一化和反余弦变换的非线性操作,可在一定程度上适应杂波对临近目标检测的影响,但在杂波区产生了虚警。导致这一现象的原因是归一化时认为杂波背景是均匀的,为了解决这一问题,类似于现有的GO-CFAR和SO-CFAR、CA-CFAR等组成的混合结构智能CFAR检测器,可在几何检测器中引入杂波区域位置的先验信息,采用分区归一化策略来避免虚警,对应的检测器可称之为智能几何检测器,其设计与分析将是下一步研究的重点。

为了考察和评估几何检测器对杂波背景的适应能力,图7给出了杂噪比从10 dB变化到30 dB时几何检测器及CFAR检测器的检测概率,其他仿真参数设置如表1所示。由图7可以看出,在本文仿真条件下,几何检测器可在18.5 dB杂波背景下以0.9的检测概率可靠检测杂波边缘处的目标。另外,对比传统的CFAR检测器,当检测概率为0.9时,几何检测器杂波背景适应能力分别优于CA-CFAR、OS-CFAR检测器8.5 dB、1 dB,低于SO-CFAR检测器7 dB。

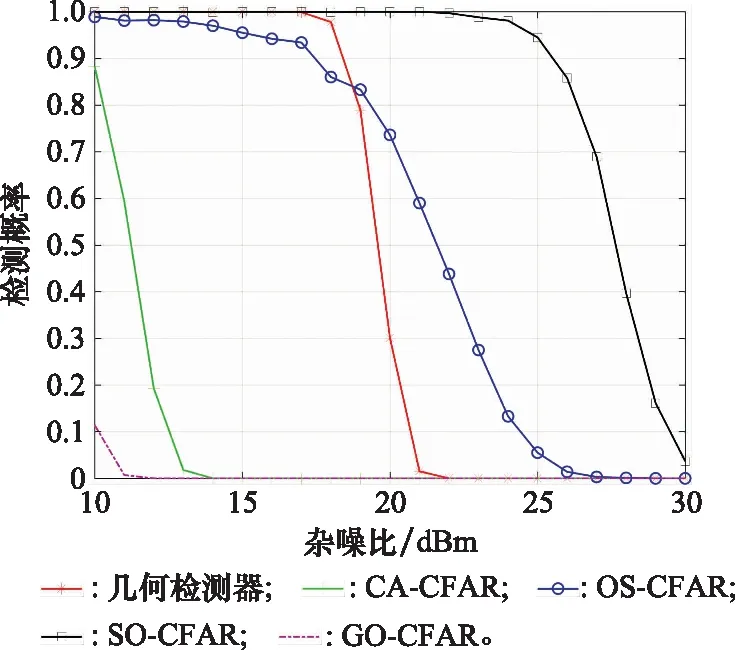
图7 杂噪比变化时检测器检测曲线

3.4 双目标检测

雷达检测中,除了杂波的影响外,另一类典型情形即多目标互扰。当待检测小信号(小目标)的参考单元内存在强信号(大目标、孤立点杂波或者欺骗干扰信号等)时,因恒虚警门限抬高将导致小目标漏报,从而形成对小目标的遮蔽效应。本节讨论强目标落在弱目标参考单元内部时几何检测器的检测性能。

假设两个功率不同的目标位于邻近的单元中,其中,强目标与弱目标分别落在第200与第210个多普勒单元,强目标的功率是弱目标的4倍,其余参数设置如表1。图8分别给出了CA-CFAR、OS-CFAR、SO-CFAR、GO-CFAR以及几何检测器的门限值,输出为归一化后的结果。图8显示了第175到第225个多普勒单元。由图8可见，CA-CFAR及GO-CFAR检测器受参考单元内的强目标影响,无法检测出弱目标;OS-CFAR和SO-CFAR均可检测出弱目标;几何检测器通过对输入数据的归一化来适应背景起伏,无需通过参考单元估计噪声功率,且反余弦变换压缩了强弱目标之间的相对大小,从而可更好地在大对比度(大动态变化)条件下检测弱目标。

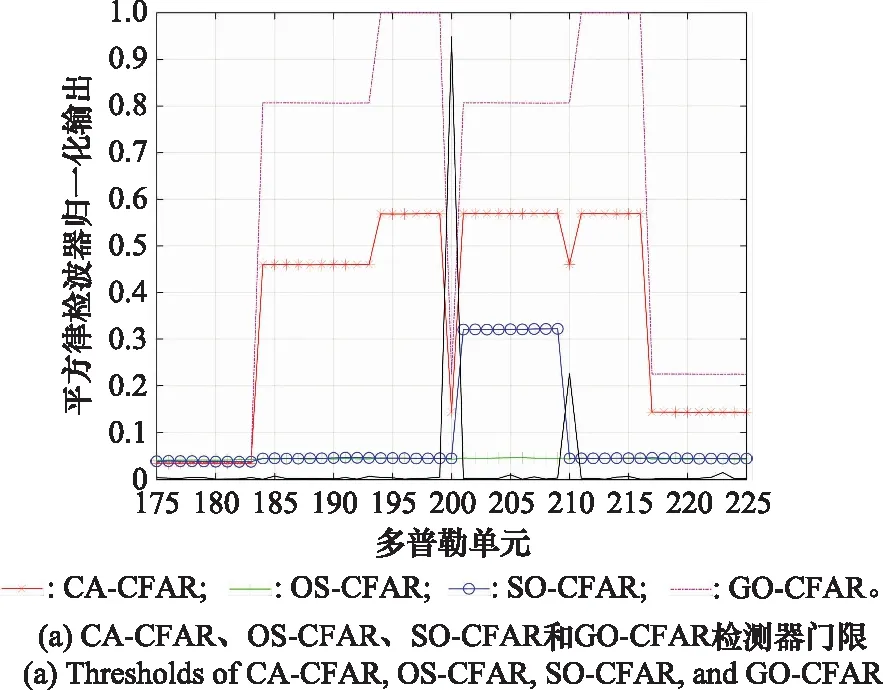
图8 4种CFAR检测器与几何检测器门限

为了评估几何检测器对强目标干扰的适应能力,图9给出了几何检测器和4种CFAR检测器检测概率随强弱目标功率比的变化关系。

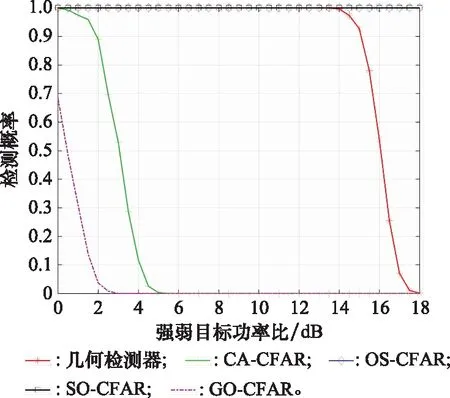
图9 不同功率比下检测器对弱目标的检测概率

由图9可以看出,OS-CFAR及SO-CFAR在不同的功率比下均可将弱目标检测出来;GO-CFAR在3 dB时已无法将弱目标检测出来;几何检测器可在15.1 dB对比度下可靠检测弱目标(检测概率0.9),相对CA-CFAR检测器对强干扰信号的适应能力提升了13.2 dB。因此,对于检测信号存在大动态变化的应用场景,几何检测器相对CA-CFAR及GO-CFAR检测器可提升对弱目标的检测能力。

4 结 论

本文针对脉冲多普勒雷达信号检测应用,基于几何代数理论,从几何视角重新理解检测器的输入信号,并设计出几何检测器。实验结果表明,在均匀背景下,几何检测器几乎无恒虚警损失;当目标参考单元有杂波干扰或是其他强信号时,几何检测器由于对数据进行了归一化以及反余弦变换,降低了背景干扰对目标检测的影响,增强了对杂波边缘及目标信号大动态变化的适应性,且结构简单易于实现。

实验中发现,当目标处于杂波边缘时,几何检测器在杂波区出现了虚警。因此,下一步将重点研究背景分区自适应的智能几何检测器。同时,对几何检测器性能与背景干扰关系的理论分析也可作为下一步的研究重点。