基于电流相位特性的滑动散射中心建模方法

袁文杰, 郭琨毅, 盛新庆, 金从军

(1. 北京理工大学信息与电子学院, 北京 100081; 2. 北京仿真中心, 北京 100854)

0 引 言

大量精确测量已经证明目标的散射场可以由若干散射中心的散射场相干叠加来描述。散射中心模型是雷达目标特性以及自动目标识别(automatic target recognition, ATR)等研究领域的热点。散射中心依据位置分布特征可以分为3类:局部性散射中心(local scattering center,LSC)、分布型散射中心(distributed scattering center,DSC)和滑动型散射中心(sliding scattering center, SSC)。其中,由光滑曲面反射所形成的SSC,是现代流线外形飞行器目标的常见散射中心,且其幅度较大,因此受到了较多的关注,已有学者提出了相应的散射中心模型。

散射中心的属性参数一般包括位置、幅度和极化信息等。提取散射中心的属性参数,首先需要从目标整体回波中将各个独立散射中心的散射成分分离,然后再确定参数。目前的研究方法可分为两类:一类基于雷达成像,即从目标合成孔径雷达(synthetic aperture radar, SAR)图像、时频像(time-frequency representation, TFR)或高分辨距离像(high resolution range profiles,HRRP)中提取散射中心的参数。图像分辨率越高,各个散射中心的图像特征越清晰,该建模方法的结果越准确;二为基于几何结构分割的方法,即根据散射机理对目标几何结构进行划分并以高频方法计算各结构的散射贡献，或采用全波法计算等效电流再分区获得局部散射源贡献,最后从独立结构的散射贡献中提取散射中心模型的参数。该方法不需要成像处理,因此建模精度不受分辨率和图像质量的限制。

以上两种方法实现散射中心建模的关键在于各散射中心散射成分的有效分离。第一种方法受限于雷达图像分辨率,因此需要目标的宽频带、宽角度散射场数据;第二种方法受局部散射贡献计算精度的影响,高频方法很难获得曲率变化较大处散射中心的位置和幅度,而采用几何结构进行电流分区的方法很难处理光滑曲面的情况,分区大小需要依据成像结果判断分区内是否包含多个散射中心而反复调整,因此建模计算效率较低。

针对SSC建模的问题,本文提出了基于目标等效电流驻相点的散射中心建模方法,通过寻找等效电流相位的驻相点来确定SSC的位置。与传统方法相比,该方法的优势包括:第一,采用自适应寻找驻相点的方法,可以精确、快速确定散射中心位置;第二,准确确定散射中心位置后,依据该位置进行电流数据分区,可以简化分区难度,提高建模效率;第三,由于表面电流分布随方位起伏远小于散射场的起伏,因此仅采用稀疏方位角采样下的表面电流数据即可实现建模,可以有效减少建模所需的散射数据量。

对于散射中心较多且集中的情况而言,在雷达图像中多散射中心的图像特征会相互遮挡,造成散射中心幅度参数的估计误差。本文采用电流分区的方法获得SSC的散射贡献,然后再进行数学建模。通过电流分区可以避免多散射中心成分混叠造成的参数提取困难问题,提高结果的准确性。根据散射中心的散射机理、目标物理结构和驻相点可以快速确定每个分区的初始范围。现有的基于电流分区的散射中心建模中,电流区域划分大小是否合适是利用时频像的图像特征进行人工判断。由于本文通过驻相点已经确定了散射中心的位置,因此可以有效避免分区内包含多个散射中心的情况,简化了建模难度。

下文以流线型带翼弹头为例,介绍了建模的具体实现方法,并通过全波法结算结果验证了建模的精度。最后以某隐身无人机为例,验证了该方法用于复杂目标的建模的有效性。通过对比可见,模型仿真获得的雷达散射截面积(radar cross section, RCS)、TFR和逆合成孔径雷达(inverse SAR, ISAR)像与全波法结果均具有较高的一致性,验证本文方法的可行性。

1 基于驻相点确定SSC位置的方法

全波法计算得到的目标等效电流源,其辐射场叠加就是目标的散射场严格解。因此,从等效电流源角度获得散射中心,相比于从雷达图像中提取强散射点,可以获得更丰富的物理信息,例如可以获得散射中心的三维位置信息,而不仅仅是距离—方位维的投影位置。并且与散射场相比,表面电流分布随方位起伏远较小,特征分析所需的角度采样数据量少。散射中心的位置参数是散射中心模型的重要参数之一。散射中心的位置精度低,其幅度参数也很难获得精确的估计结果。

根据电磁理论和驻相点原理可知,每个散射中心都相当于Stratton-Chu积分中的一个数学不连续处,即目标表面曲率不连续处和驻相点处即对应散射中心的位置。基于此判断,结合散射中心形成机理,可以通过目标表面曲率不连续处确定局部性和分布型散射中心的位置,通过寻找目标表面电流相位的驻相点确定SSC的位置。具体的过程如下。

首先,采用全波法计算目标的等效表面电流。本文采用矩量法(method of moment, MoM)结合并行多层快速多极子算法(parallel multi-level fast multipole algorithm, PMLFMA)计算电流。由于电流起伏小于电场,因此这里方位角度采样间隔为Δ=5°就可以很好拟合散射中心位置。

获取等效表面电流数据库后,采用自适应方法寻找目标表面等效电流的驻相点。驻相点与其周围相位相差很小,通常先计算相位的差分,然后寻找最小极值点来确定驻相点位置。然而,由于驻相点周围的相位相差都很小,因此相位极值点很多,很难单凭极值点判断来确定驻相点。而且,电流数据是三维立体模型上的,但是按照矩阵形式存储,由于几何建模和剖分原因,并不能保证在矩阵中相邻的电流数据实际在模型上的位置也是相邻的,直接对矩阵求差分数据结果会存在错误值,而且每个目标的情况不同,因此该问题很难避免。

为此,本文寻找驻相点的方法是直接根据电流点坐标位置来求一定区域内的平均相位差,并根据结果自动调整区域大小,如图1所示。考虑到网格离散一般为/10(为入射波波长),光滑表面电流相位的变化周期大于或等于波长,因此该方法中最大计算区域小于波长。

图1 自适应寻找驻相点

具体搜索过程如下:设(=1,2,…,)表示以半径为区域的点,表示点的个数,表示区域的中心点,phase()表示点的电流相位,表示中心点与所有点的平均相位差:

(1)

若该点平均相位差小于阈值,即≤,则记为驻相点,并计数=+1(初值为0)。改变中心点的位置,重复式(1),遍历该区域可以找出目标等效电流相位的所有驻相点。式中,半径的设置要结合目标的几何结构和剖分尺寸设定,若值太小,则可能造成误判,使偏大;若值太大,则可能造成漏判。因此,本文设定了自适应修改区域大小的方法,若所有点均不满足≤条件,即=0,减少值(=-Δ,Δ=05),重新计算,直到值小于波长时退出。具体流程图如图2所示。

图2 自适应寻找驻相点流程图

2 基于驻相点确定SSC位置的方法

确定稀疏观测角度下的驻相点后,经拟合获得散射中心的连续变化位置。根据3类散射中心的散射机理、目标物理结构和驻相点可以确定每个分区的初始范围。散射中心建模的流程图如图3所示。其中DSC和LSC的建模方法参照文献[25],本文不再赘述。

图3 建模流程图

下文以弹头为例,给出散射中心建模的实现步骤。目标模型的构建与剖分可以借助ANSYS或CATIA等软件构建。使用CATIA构建的某导弹模型如下。该目标模型总长约2.8 m,总宽约1.8 m,选取计算散射频率3 GHz,雷达观测角度范围取=90°,=0°(是方位角，是俯仰角)。头部为双曲面结构,尾翼为扁平的椭球体(三轴比为006∶02∶1122)。

图4 某导弹模型

2.1 散射中心位置估计

对于弹头而言,SSC主要由双曲面上的镜面反射,其位置随入射角度变化,这里采用驻相点来确定。弹头底部曲边也有一个绕射形成的SSC,其位置为回转轴与入射线构成的平面与底部边缘的交点,其建模方法可参考文献[9]。当入射角为=30°,=0°,弹头的电流相位分布如图5所示,两个驻相点的位置也已在图中标出。

图5 某导弹模型的两个驻相点

考虑观测角度范围为=0°～90°,=0。

通过驻相点找出的两个散射中心位置变化以及函数拟合结果如图6所示。拟合用到的是稀疏角度下的驻相点位置,角度间隔为Δ=5°。为了验证两个SSC位置的提取精度,图7给出了全波法计算结果通过时频变换获得的多普勒特征曲线,由所提取的散射中心位置变化计算得到的多普勒曲线也在图7中给出。虚线与TFR中的曲线具有恨到的一致性,验证了散射中心位置的精确性。

图6 两个散射中心位置变化以及函数拟合结果

图7 SSC多普勒位置和时频像

2.2 确定分区

以入射角度=0°～90°,=0°为例,弹头曲面上的滑动散射中心为SSC1,临近的散射中心为DSC1。由于双曲面和单曲面差别明显,因此可以按照几何结构直接进行电流分区。对于尾翼棱边上的SSC2,临近的散射中心有LSC1。因此分区时需要除去LSC1的区域。LSC1为局部型散射中心,其分区为以顶点为中心,半径为波长的范围。该导弹具体分区以及分区电流的贡献如图8所示。

图8 某导弹分区

2.3 散射中心幅值参数估计

确定了电流贡献区域之后,可以直接积分计算得到散射场。依据散射中心模型分别对散射场进行参数拟合即可得到散射中心模型的幅度参数。SSC模型的数学表达式可写为

(2)

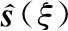
弹头的两个SSC的散射场贡献及拟合结果如图9和图10所示。其中,散射波频率为3 GHz,极化方式为VV极化,与数值计算相比,均方根误差分别为0.016 V/m和0.011 V/m。SSC1和SSC2幅值均为阶数=9的多项式函数,具体参数如表1所示。

图9 SSC建模结果

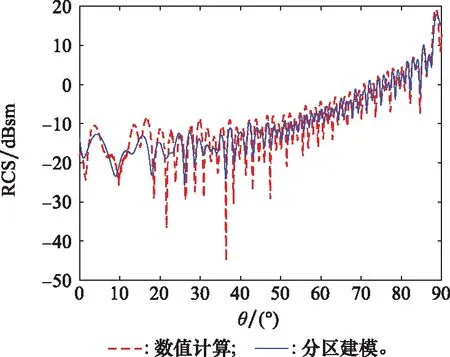
图10 RCS结果对比

表1 SSC1和SSC2幅度参数

3 复杂目标的散射中心建模

为了验证该方法对于复杂目标的有效性,以复杂隐身无人机目标为例,给出了该方法建模结果以及与全波结果的对比验证,并与传统建模方法进行了横向对比。隐身无人机三维模型如图11所示。

图11 隐身无人机几何模型

上述无人机模型是一个典型流线型赋型设计的隐身飞行器,飞机采用蝙蝠型双翼与翼身融合的飞翼曲面构型,很难通过外形直观判断SSC分布位置。本文采用了自适应寻找驻相点的方法确定背部SSC散射中心位置,再依据散射中心位置进行电流分区,具体分区结果如图12所示。总共分为了34个区,包含两个SSC分区,20个LSC和12个DSC分区。

图12 隐身无人机分区结果

采用MLFMA方法计算得到的无人机表面电流数据。散射频率为3 GHz,观察角度为=0°～90°,=90°,角度采样间隔取Δ=5°。图13给出了入射角度为=15°,=90°时的电流相位值分布。采用自适应寻找驻相点方法,准确确定出了SSC位置。

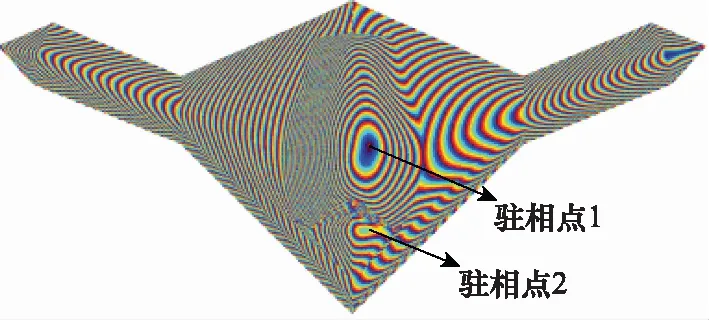
图13 隐身无人机相位

基于第2节所述的散射中心建模流程,建立了无人机的完整散射中心模型。图14～图16分别是使用全波方法、基于电流相位的分区建模方法和传统建模方法计算的散射场时频像。图17是RCS结果对比,图18是使用分区建模方法计算得到的ISAR图像和三维模型的对比。其中,计算ISAR频率为=2.5～3.5 GHz,间隔取Δ=100 MHz,角度为=-90°～90°,=90°,角度采样间隔取Δ=0.1。

图14 数值计算时频像

图15 分区建模时频像

图16 传统建模时频像

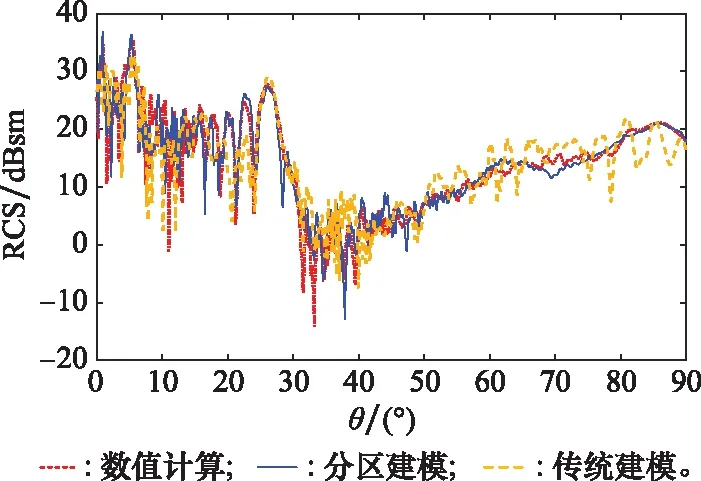
图17 3种计算方法的RCS对比

图18 隐身无人机ISAR图像和三维模型

3种方法计算耗时如表2所示。其中,分区建模方法需要多次调整、细化分区以提高计算精度。传统建模方法需要多次使用遗传算法迭代估计,该无人机的散射中心待估参数为76个。RCS计算时间指分别使用已建立的数学模型计算RCS的时间(DELL 3668-R2938,CPU i7-7700),和利用MLFMA计算RCS的时间(IBM系统x3650M5,CPU 2.2 GHz),计算频率为=3 GHz,角度为=0°～90°,=90°,角度采样间隔取Δ=0.1。

表2 计算时间统计

3种方法的精度比较如表3所示。使用基于电流相位的分区建模方法计算的结果与数值结果的时频像相关系数更高,RCS误差更小,即计算结果更加精确,并且ISAR图像和三维模型较好重合,验证了基于电流相位的分区建模的计算精度。

表3 计算精度对比

4 结 论

本文提出了一种基于等效电流驻相点的散射中心位置提取方法,该方法适用于曲面反射形成的SSC。将该方法与电流分区结合,实现了复杂目标的散射中心精确建模。基于SSC已知位置进行电流分区,可以避免分区包含多个散射中心的问题,简化分区难度。此外,有效电流分区可以解决多散射中心成分混叠造成的参数提取精度低的问题,同时仅采用稀疏方位角采样下的表面电流数据即可实现建模,大大减少了建模所需的散射数据量。以流线型结构为主无人机为例,本文通过全波法结果对建模精度进行了验证,并与传统建模方法进行横向对比,结果表明基于电流相位的散射中心模型对于RCS起伏模拟和时频像仿真,均具有较高的精度。