基于长短期记忆循环神经网络的伊拉克H 油田碳酸盐岩储层渗透率测井评价

杨旺旺 张 冲 杨梦琼

张亚男1，2 汪明锐1，2 孙 康1，2

（1. 油气资源与勘探技术教育部重点实验室（长江大学），湖北武汉 430100；2. 长江大学地球物理与石油资源学院，湖北武汉 430100）

0 引 言

碳酸盐岩储层是一种十分重要的油气储集层，其勘探开发潜力巨大［1］，在世界油气分布中有着必不可缺的地位。渗透率是指在一定外界压力下，岩石允许流体通过的性质，是油气田开发生产中的一项重要参数，其与储集层产能预测、资源勘探开发息息相关［2］。伊拉克H 油田S 层段和T 层段是典型碳酸盐岩储层，其孔隙结构复杂，孔隙度与渗透率之间不再是比较明显的线性关系，因此通过测井资料评价其储层渗透率是一个非常棘手的问题。

砂岩储层渗透率与孔隙度的相关性一般较好，然而碳酸盐岩储层渗透率与孔隙度的相关性远不如砂岩储层［3］。国内外学者对储层渗透率的定量评价进行了一系列研究，评价方法多种多样，相对准确且直接的方法是实验室直接测量［4］，但其测量成本高，测量方式复杂，难以进行全井段测量。国内外学者相继提出了多种渗透率评价模型，如通过渗透率与各储层特征参数间的强烈非线性关系而建立的渗透率模型，主要有Kozeny‐Carman公式、Timur 方程、Wyllie‐Rose 方程［5］以及基于等效岩石组分理论的渗透率方程［6］，考虑到渗透率受孔隙微观结构的影响，不少学者又提出了更加精细的渗透率评价模型，如WinlandR35 模型［7］、Swanson 模型［8］、Capillary‐Parachor 模型［9］等。以上根据渗透率与储层特征参数或孔隙结构参数的非线性关系建立的渗透率模型，都需要在建模前开展岩石物理实验，才能获得各个参数与渗透率的非线性映射关系，并且有些参数不能准确获得，容易造成一定的误差。而利用测井响应参数与渗透率的非线性关系构建渗透率模型相对比较简单，无需开展岩石物理实验，如核磁共振渗透率模型［10］、斯通利波渗透率模型［11］和常规机器学习模型［12］，但这些模型在碳酸盐岩储层中应用效果一般，前两种模型属于非常规测井模型，不适用于非均质性强的碳酸盐岩储层，而常规机器学习模型在建模过程中需要人工进行特征提取，属于比较简单的浅层机器学习神经网络，很难表示繁杂的非线性映射关系。

地球物理测井参数从不同深度点反映了各个地质时期的声波、放射性、电性等沉积特征，故测井响应参数与渗透率之间存在较强的非线性映射关系且具有时间序列性质［13‐14］。为此，本文采用深度学习的方法，考虑到测井响应参数与渗透率具有一定的时间序列性质，搭建了具有记忆功能的长短期记忆网络，并通过交叉验证对网络的拟合能力进行综合评估，进而调节网络超参数直到网络拟合能力达到最优，然后重新训练模型，并用训练好的LSTM 网络模型进行渗透率预测，最后用实际数据来验证模型的预测效果和实用性。同时，为了证明LSTM 模型预测渗透率的优势，本文构建了同样以处理时间序列为基础的灰色系统GM（0，N）模型，并采用皮尔逊（Pearson）、肯德尔（Kendall）、斯皮尔曼（Spearman）三种相关性系数定量计算渗透率与测井数据的相关程度，优选测井参数并分别进行建模，用同样的数据进行对比测试。

1 基本原理

1.1 长短期记忆网络

常规的循环神经网络（RNN）只能处理一定的短时序列问题，无法处理长程依赖问题。因为当序列数据较长时，序列后端的梯度很难反向传播到前端的序列，容易产生梯度消失问题和梯度爆炸问题。长短期记忆网络也叫LSTM 循环神经网络，是RNN 的一种变体，可以有效地解决梯度消失和爆炸问题， 最早由 S. Hochreiter 和J.Schmidhuber 在1997 年提出［15］。相比常规RNN 网络，LSTM 网络的循坏单元更加复杂，在循环单元中增加门控机制，这样使得循环单元的权重是可变的，这种带有门控结构的循环单元可以有选择地保存有用历史信息，遗忘无用历史信息。因此可以避免梯度消失或者梯度爆炸的问题。

图1 为LSTM 网络在t时刻的循环单元结构［16］。如图1 所示，首先需要将t−1 时刻的隐藏层的输出和t时刻的输入分别复制4 份，并随机初始化不同的权重，然后将ht-1与xt向量进行拼接，最后通过激活sigmoid 函数或tanh 函数进行非线性转化得到遗忘门、输入门、输出门激活向量和经过变换后的神经元细胞状态向量，其计算公式为：

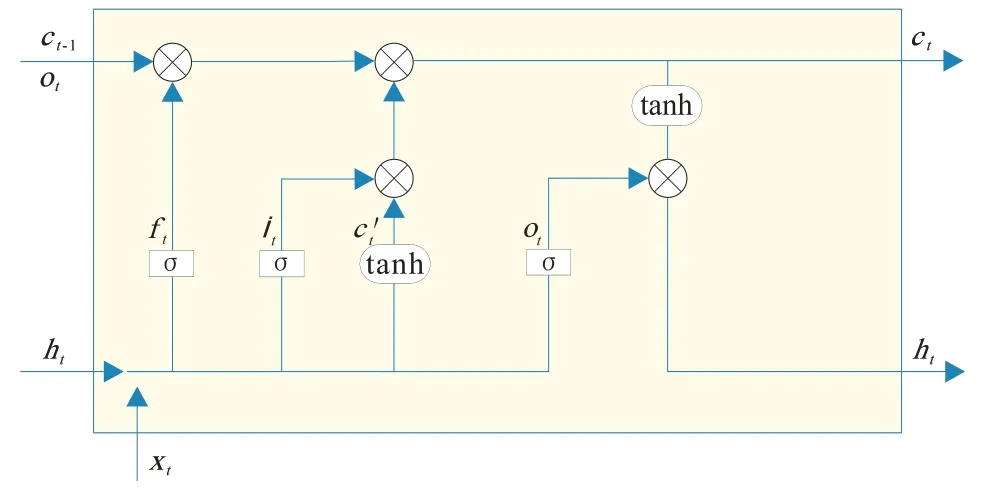
图1 LSTM网络t时刻循环单元工作原理Fig.1 Working principle of recurrent unit for LSTM network at t time

式中：ft、it和ot——t时刻的遗忘门、输入门、输出门的激活向量；c't——t时刻经过tanh 层变换后得到的神经元细胞状态向量；W——权重矩阵；b——偏置矩阵；xt——t时刻的输入；ht-1——t−1时刻的隐藏层的输出；σ——sigmoid 激活函数。

遗忘门ft和输入门it分别用来舍弃部分无用的存储单元信息和保留t时刻部分有用信息，从而更新内部储层单元ct，其计算公式为

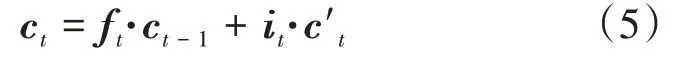
式中：ct——在t时刻更新过后的存储单元；ct-1——t−1 时刻所保留下来的存储单元。

输出门ot可以挑选ct的有用信息并传入到隐藏层ht，其计算公式为

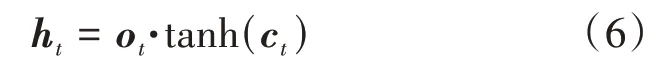
式中ht——t时刻隐藏层的输出。

1.2 基于LSTM 循环神经网络的渗透率测井评价模型框架

LSTM 循环神经网络模型结构与全连接神经网络结构类似，包含输入层、隐藏层和输出层，其隐藏层是网络结构中的核心结构。理论上神经元数目越多，网络结构越深，其网络拟合效果就越好，预测精度越高。但在实际应用中，需要考虑样本数据量的大小，以及样本特征的维度等因素，如构建的隐藏层层数和神经元数目过多会导致网络训练耗时过长，并且容易造成过拟合，反之也会造成欠拟合。

本文构建的LSTM 循环神经网络的循环单元对时序数据处理的特性，其循环单元本身就属于一个较深的结构。所以构建的网络结构的隐藏层为1个LSTM 层，2 个全连接层（Dense layers），共3 个隐藏层，确定了网络层数之后，还会用到K 折（K‐ford）交叉验证（cross validation）算法进行实验，从而来确定隐藏层神经元的个数、学习率等超参数。

本文中搭建的渗透率测井评价框架包括数据预处理、输入层、LSTM 层、全连接层以及输出层5 个部分，其中在数据预处理部分，首先会进行多井标准化、扩径校正、岩心归位、数据清洗以及敏感曲线的选取，确保输入数据的准确性，预处理完成之后就划分训练集和测试集并依次传入网络的输入层、隐藏层，并进行迭代求解，直到模型收敛最后输出，最终形成基于LSTM 循环神经网络渗透率测井评价模型框架（图2）。

图2 基于LSTM循环神经网络渗透率测井评价模型框架Fig.2 Permeability logging evaluation model framework based on LSTM recurrent neural network

1.3 灰色系统GM(0，N)模型

本文采用灰色系统模型来作为对比模型，灰色系统是由邓聚龙［17］在1982 年提出用来解决信息不完备系统的机器学习方法，常用于处理时间序列问题。

GM（0，N）是最简单的灰色系统模型，不含导数，属于静态模型，与多元回归模型有着本质区别，一般多元回归是以原始数据序列为基础进行建模的，而GM（0，N）是以原始数据的1‐AGO序列进行建模的，该模型的建模形式弱化了原始数据的随机性，提高了数据的规律性。

2 实验与分析

2.1 应用工区概况

伊拉克H 油田的S 和T 层组是该油田的主力油组，主要发育生物碎屑灰岩、孔虫粒泥灰岩、生屑颗粒灰岩等岩相，受构造作用、成岩作用以及储集空间复杂性的影响，该储层的非均质性较强。图3 为岩心孔渗的交会，可以看出孔隙度与渗透渗之间的线性关系并不明显。概括来讲，研究区目的层组具有岩相复杂、孔隙空间较小、孔隙结构以及孔隙类型繁杂多样等特点，从而导致该层组的渗透率评价难度加大。

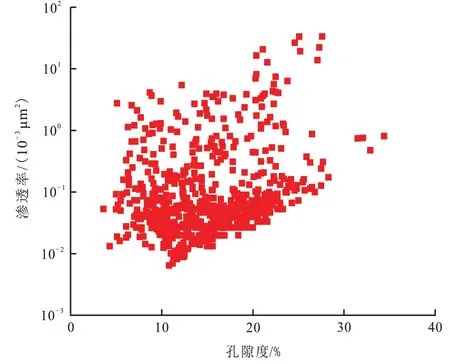
图3 岩心孔渗交会图Fig.3 Cross plot of porosity vs.permeability of the core

2.2 数据准备

本文的数据来源于伊拉克H 油田实际勘探的测井数据，共选取906 组测井数据样本，包括自然伽马（qAPI）、自然电位（VSP）、深侧向电阻率（RLLD）、浅侧向电阻率（RLLS）、声波时差（Δt）、补偿中子孔隙度（ϕCNL）、补偿密度（ρRHOB）、泥质含量（φsh）以及对应的渗透率，其中泥质含量（φsh）是由中子−密度交会计算而得，是补偿中子孔隙度和补偿密度两条曲线的综合反映，故将泥质含量这个参数作为一个初步的计算参数，之后对上述测井参数进行相关性分析，最后确定出模型的输入参数。渗透率由实验室直接测得。在将样本数据输入网络之前需要将数据集划分为训练数据、测试数据。共选择了234 组测井数据作为测试数据，剩下的数据作为训练数据用来训练模型。

2.3 参数相关性

分别采用皮尔逊（Pearson）线性相关系数P、肯德尔（Kendall）秩相关系数R和斯皮尔曼秩相关系数S来定量计算各个测井参数与渗透率的相关性，并优选测井曲线，避免赘余的信息和多重共线性影响模型的泛化能力。3 个相关性系数的计算公式为：

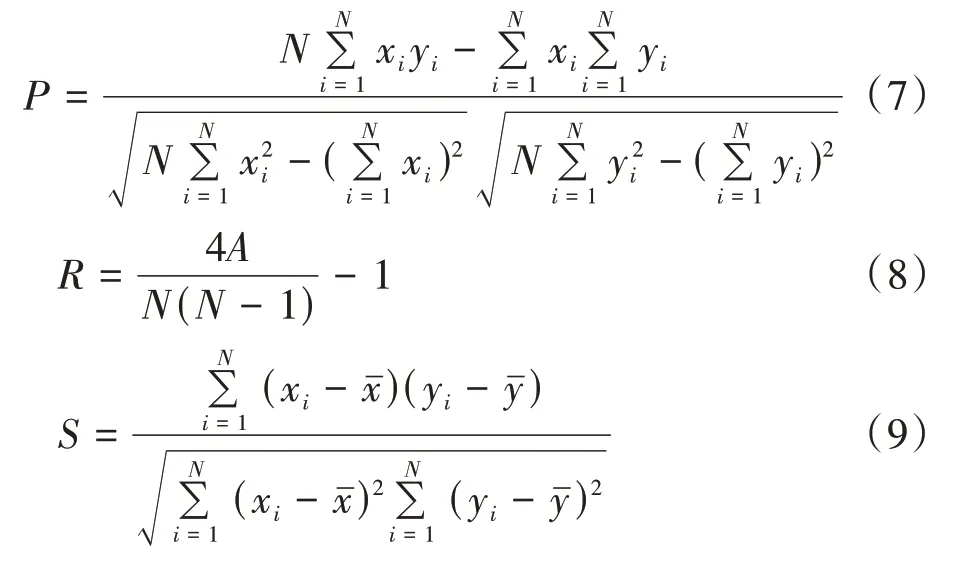
式中：x——各个常规测井参数；y——岩心渗透率；i——每个样本的序号；N——统计的总样本数；A——两个属性值排列大小关系一致的统计对象对数；xˉ——常规测井参数的均值；yˉ——岩心渗透率的均值，10−3μm2。

各测井参数与渗透率的3 种相关度绝对值的变化趋势如图4 所示。从图4 可以看出，自然伽马、泥质含量、补偿密度、声波时差、补偿中子孔隙度这5 种测井参数的P、R和S均较高，说明渗透率与qAPI、φsh、Δt、ϕCNL、ρRHOB之间存在较强的相关性，VSP的P较高但S和R较低说明自然电位与渗透率之间只存在一定的线性相关，非线性相关程度较弱，RLLD和RLLS的P、R和S均较低。因此最后选择自然伽马、泥质含量、声波时差、补偿中子孔隙度、补偿密度这5 种测井参数预测渗透率。

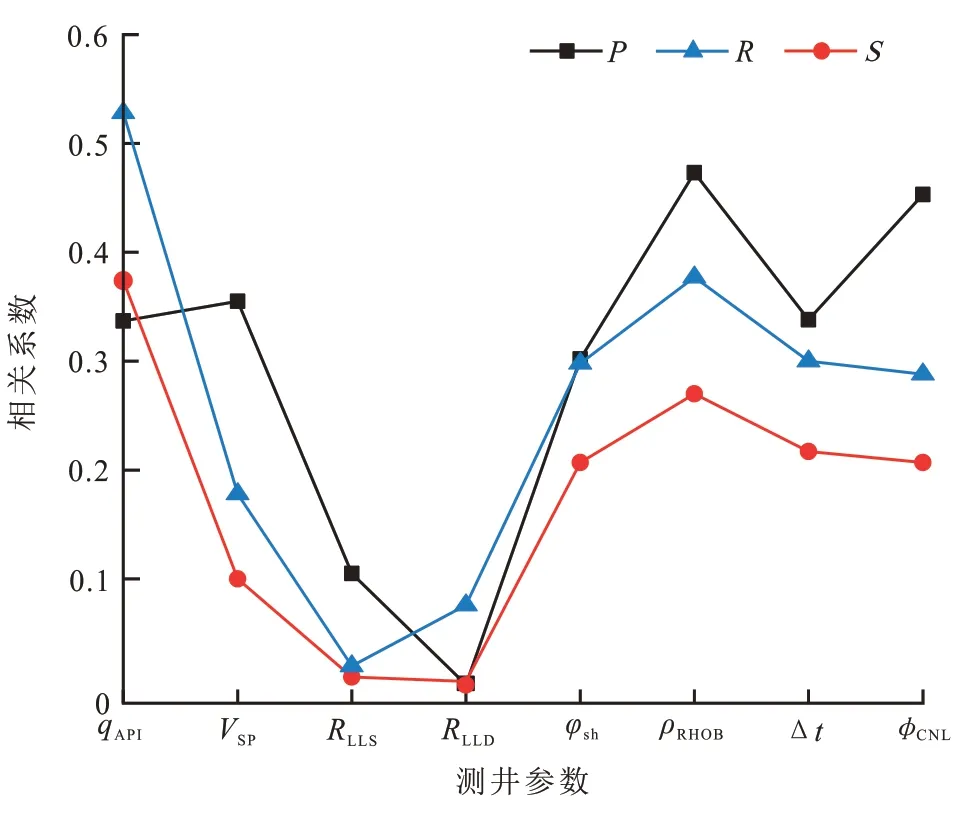
图4 测井参数与渗透率关联程度Fig.4 Correlation degrees between logging parameters and permeability

2.4 数据标准化

在构建模型之前，为了减小因输入数据差距过大而造成预测误差，需要将输入数据调整到一个合理的分布范围，也就是需要将输入数据进行标准化处理，因此本文选择了z−score 标准化方法，其标准化处理的表达式为

式中：yi——输入参数；yˉi——该输入参数的均值；s——该输入参数的标准差；y*——该输入参数标准化后的数据。

2.5 预测结果评价方法

本文采用Pearson 相关系数P和均方根误差ERMSE（root mean squared error）来共同评价预测结果的准确性，Pearson 相关系数用来衡量预测结果与真实值之间的线性相关程度，均方根误差用来衡量预测结果与真实值之间存在的偏差。P的计算公式见式（7），ERMSE的计算公式为

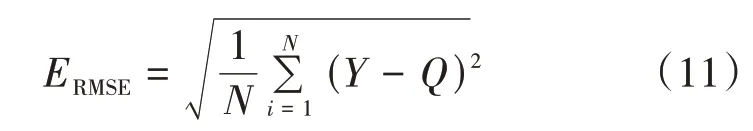
式中：Y——预测结果值；Q——真实值。

P值越大，表示预测结果与真实值线性相关程度越高，ERMSE越小，表示预测结果与真实值存在的偏差越小，说明模型的拟合能力越强。

2.6 模型训练及参数调优

采用的自适应优化算法（Adam）是一种随机梯度下降算法的改进，具备自适应学习率优化算法（AdaGrad）和梯度下降算法（RMSProp）的优点，隐藏层的激活函数采用的是线性整流函数（Relu），也叫Relu 激活函数，该激活函数为非线性函数，能够使网络更好地解决复杂非线性问题，并且Rleu 函数能够克服一定的梯度消失问题。

采用了K 折（K-fold）交叉验证算法来确定隐藏层神经元的个数、学习率，防止过拟合。首先初步设定学习率（learning rate）a=0.001，喂入网络的批量大小（batch size）为10；迭代次数s为20；隐藏层的神经元个数设置为2n，n取值范围为［2，8］，则神经元的个数分别取4、8、16、32、64、128、256 顺次进行训练，其实验结果见图5。

图5 不同神经元个数的预测误差Fig.5 Prediction errors of different numbers of neurons

图5 中横坐标为隐藏层神经元个数，纵坐标为所预测渗透率的均方根误差，可以看出当神经元个数小于32 时，均方根误差偏大，当神经元个数为64 时，均方根误差达到最小值，然后随着神经元个数不断增多其均方根误差逐渐变大。因此确定了隐藏层的神经元个数为64 个。图6（a）展示了不同学习率下的LSTM 模型的预测精度随迭代次数的变化关系，可以看出在a=0.01 时，ERMSE曲线下降最快，收敛速度最快并且最平缓，所以设定a=0.01 为LSTM 模型的学习率。为了验证LSTM 模型是否存在过拟合以及解决方法，分别使用了神经元随机丢弃算法（Dropout 技术）和L2 正则化方法来进行试验，如图6（b）所示，不使用方法的型其ERMSE曲线收敛速率一般，收敛后出现了过拟合现象，使用L2 正则化方法的模型其ERMSE曲线收敛速率较低，收敛后处于比较平稳的状态，采用了Dropout 技术的LSTM 模型其ERMSE曲线收敛速率高且收敛后达到平稳状态，Dropout 技术在这个模型中不仅消除了一定的过拟合现象，还提升了LSTM 模型的拟合性能，本文选定Dropout 技术来防止过拟合问题。

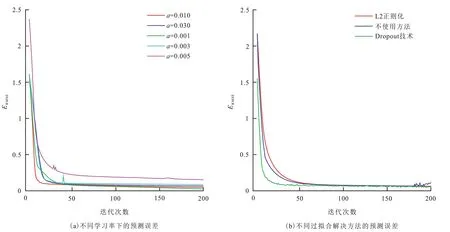
图6 不同学习率以及不同过拟合解决方法下的预测误差Fig.6 Prediction errors under different learning rates and overfitting solutions

2.7 结果分析

根据相关性分析结果，选取自然伽马、补偿中子孔隙度、声波时差、补偿密度、泥质含量5 种测井参数作为输入数据，进行标准化处理后，分批喂入已经训练过并设置了最优超参数的LSTM 网络，对渗透率进行预测。同样将上述5 种测井参数作为灰色系统GM（0，N）的输入，建立GM（0，5）预测模型。

LSTM 网络模型和GM（0，5）模型预测的渗透率Pearson 相关系数和均方根误差见表1。从表1可以看出，LSTM 模型预测结果的均方根误差要明显 的 小 于GM （0，5） 模 型，降 低 了29.47%。LSTM 模型预测结果的Pearson 相关系数明显大于GM （0，5） 模型，提高了6.59%。图7（a） 为GM （0，5） 模型预测渗透率与岩心渗透率关系；图7（b）为LSTM 模型预测渗透率与岩心渗透率关系，从图7 可以看出LSTM 模型不仅预测的精度更高，并且鲁棒性更好，也证实了LSTM 模型在预测具有时序性质的渗透率时优势明显。

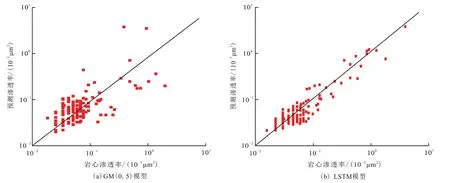
图7 GM(0,5)模型和LSTM模型预测渗透率与岩心渗透率关系Fig.7 Relations between core permeability and predicted permeability by GM(0,5)model and LSTM model

表1 渗透率预测模型的预测精度Table 1 Accuracy of permeability predicting model

图8 为2 种模型预测成果，可以看出，通过LSTM 模型预测得到的渗透率与真实值吻合程度要高于GM（0，5）模型，在S_a2 层位，2 种模型的渗透率预测效果比较接近，但仍然是LSTM 预测精度要稍高。从S_b1 至T 层位，LSTM 值，测井响应参数的变化趋势变得复杂，各测井对渗透率的预测优势更明显，主要是因为S_a2 层位的测井响应参数变化趋势比较平稳，2 种模型的渗透率预测精度都比较高，随着深度加深，从S_b1 至T 层位，渗透率存在很多突变的峰谷响应参数与渗透率之间的非线性关系更复杂，但渗透率与测井响应参数的序列性更强，普通的机器学习方法在样本有限的情况下表示复杂映射关系的能力有限，故GM（0，5）模型不能准确学习渗透率的变化趋势，从而导致该模型预测的准确性下降。对比可知，LSTM 模型具有能够提取到渗透率与测井响应参数之间的序列信息的优势，因而使得LSTM 模型能较准确预测到渗透率的振荡规律，LSTM 渗透率预测模型更符合渗透率曲线随深度变化的趋势。

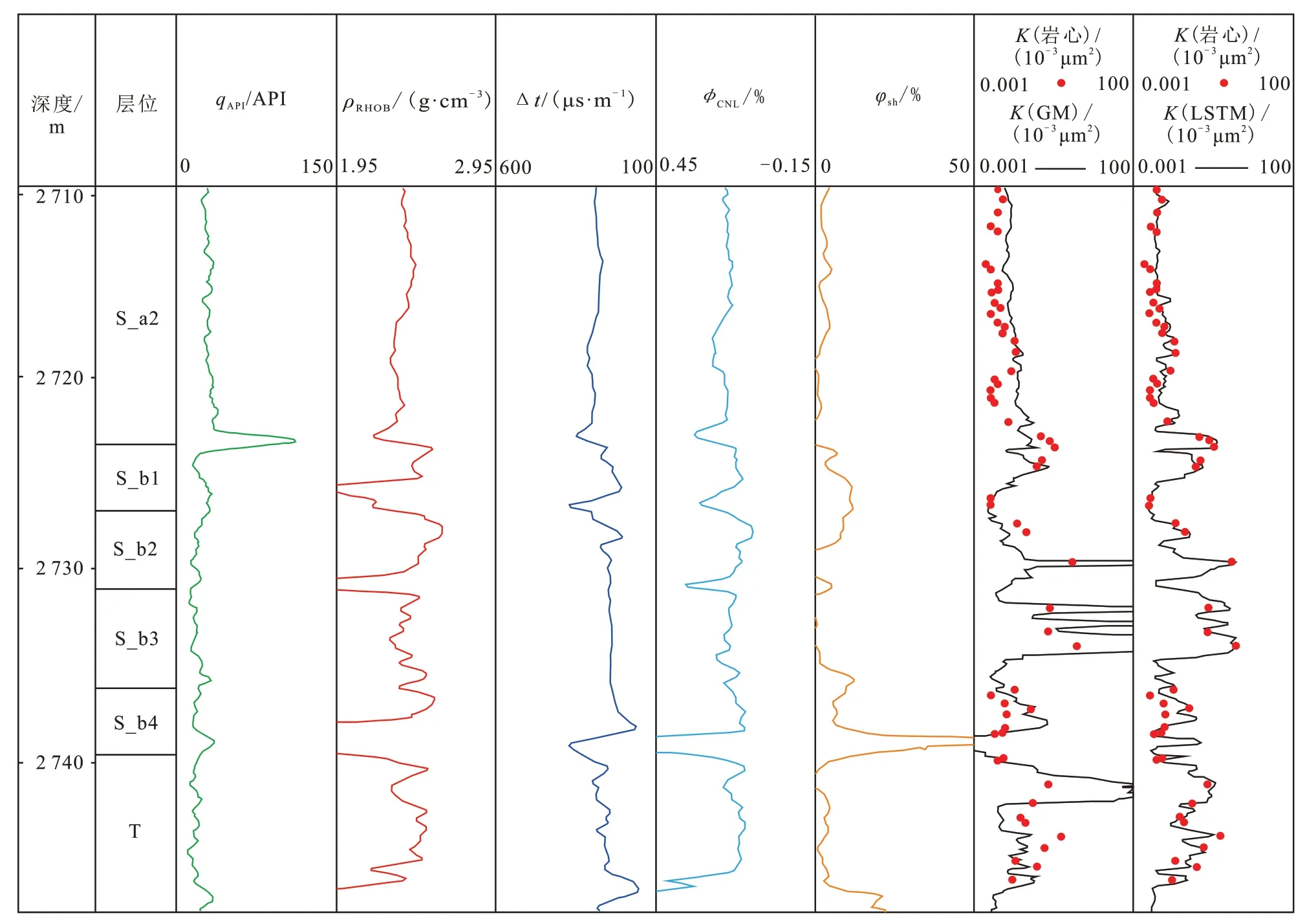
图8 2种模型预测成果Fig.8 Predicted results of 2 models

3 结 论

（1）本文介绍了LSTM 模型在碳酸盐岩储层渗率预测中的应用，采用了3 种不同相关性分析方法筛选出渗透率的敏感曲线作为模型的输入，并采用了K‐fold 交叉验证算法进行网络参数调优，最后用实际数据验证了LSTM 模型相较于常规机器学习模型GM（0，N）的有效性和实用性。

（2）直接利用测井响应参数预测渗透率大大降低了岩石物理实验和非常规测井方法的高成本。LSTM 模型可有效提取测井响应参数的特征，挖掘各测井响应参数和渗透率之间隐含的非线性关系。