压裂后页岩油藏多裂缝直井产能模型——以鄂尔多斯盆地页岩油井为例

董 鹏 陈志明 于 伟

（1. 中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249；2. 美国得州大学奥斯汀分校，美国得克萨斯州 78712）

0 引 言

页岩油开发在非常规油气能源中比例越来越大，已成为重要的油气接替资源之一［1‐2］。为提高单井产能和油田采收率，大型压裂直井已初步应用到页岩油藏中［3‐5］。对于大型压裂井，产能评价是其实际生产的首要任务［6‐7］。鄂尔多斯盆地页岩油藏主力油层脆性指数为39%～45%，属于低脆性油藏［8］。同时，储层非均质性较强，在直井进行大型压裂后，压裂井井筒附近会形成复杂多分支裂缝［9］，为其产能评价带来了困难。因此，有必要进一步完善大型压裂直井的产能评价体系。

针对大型压裂直井，目前主要有2 种简化物理数学模型：径向复合模型和离散裂缝模型。M.Chang等［3］利用径向复合模型模拟大型压裂直井的控制区。在此基础上，H.Arvind 等［4］基于微地震数据建立了大型压裂直井的径向复合模型，并基于数值解研究了大型压裂直井产能。针对数值解受网格划分及算法限制，刘雄等［5］根据储层改造程度建立了径向复合模型，得到了考虑渗透率敏感效应影响下的大型压裂直井产能方程。径向复合模型在一定程度能较好地模拟大型压裂后地层，但对于单重介质和复杂边界的页岩油藏，由于缺少天然裂缝的有效沟通，应用径向复合模型存在一定不足。

为克服复合模型的局限性及对比大型压裂与常规压裂的开发效果，一些学者［10‐13］利用离散裂缝模型来模拟大型压裂直井及评价其产能。然而，受网格数量限制，数值模型难以真实地反映裂缝特性。程林松等［14‐15］和李璗等［16］也曾提出多分支裂缝井模型的产能方程，但遗憾的是裂缝被视为完全对称且为无限导流。实际上，受地质和工程因素影响，裂缝长度、导流能力及缝间角度具有不对称性。陈志明等［17］和Z.Chen 等［18］在线性流动条件下，应用保角变换，分别推导了不对称多分支裂缝直井稳态和拟稳态产能预测模型，但模型未考虑非线性渗流因素和复杂边界形态。D.P.Craig 等［19］和D.P.Restrepo 等［20］分别利用点源解和叠加原理得到复杂裂缝直井模型的半解析产能方程，但裂缝被假定为无限导流。目前，大型压裂技术主要针对页岩储层，页岩油藏不但存在流体的非线性流动，而且经过大型压裂后还会形成非圆形体积改造区。因此，在产能评价时，亟需一套考虑非线性因素和非圆形边界影响的大型压裂直井解析产能模型。

基于离散裂缝模型，在上述研究基础上［17‐18］推导出了适用于鄂尔多斯盆地页岩油藏大型压裂直井的拟稳态产能模型。为检验方程的正确性，利用现有的常规裂缝井产能模型进行退化验证并利用数值模拟方法进一步验证。最后，分析了裂缝长度、裂缝导流能力、裂缝数目及应力敏感系数等因素对大型压裂直井产能的影响。

1 物理模型

考虑非圆形泄流区域，以六面体为例，建立简化的大型压裂直井物理模型（图1）。油井控制区包含人工裂缝和天然油藏。受地质和工程因素影响，在大型压裂改造过程中，裂缝沿井筒呈不对称网状分布，利用X轴正半轴起逆时针方向，第i个角度表征为θ=θi，i= 1，2，…，n，n为裂缝间夹角数。

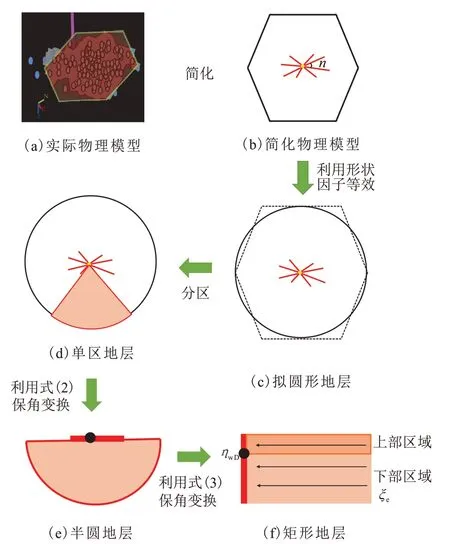
图1 大型压裂直井保角变换示意Fig.1 Schematic diagram of conformal transformation of LSF verticalwell

考虑页岩油藏渗透率的应力敏感效应。建立物理基本假设：（1）沿井筒存在不对称分布的复杂裂缝；（2）裂缝高度等于地层厚度；（3）复杂裂缝中流体线性流动；（4）不考虑垂向流动及裂缝污染；（5）油井控制区上下封闭；（6）流体流动达到拟稳态；（7）流体为单相、微可压缩牛顿流体；（8）渗流过程中等温；（9）考虑应力敏感效应。

2 数学模型

采用保角变换［21‐22］对大型压裂直井的非圆形地层进行处理。

首先，利用形状因子［23］将非圆形地层等效为拟圆形地层（图1（c）），可得拟稳态条件下等效泄流半径，即

式中：re——等效半径，cm；下标e 表示边界；A——泄油面积，cm2；CA——形状因子。

式中：Z——复变函数；θ1——半缝间夹角，rad。

将W1平面的半缝变换到W2平面上，无因次宽度为π。W1平面的地层半圆变成W2平面的矩形，如图1（f）。根据保角变换公式（2）变换后为

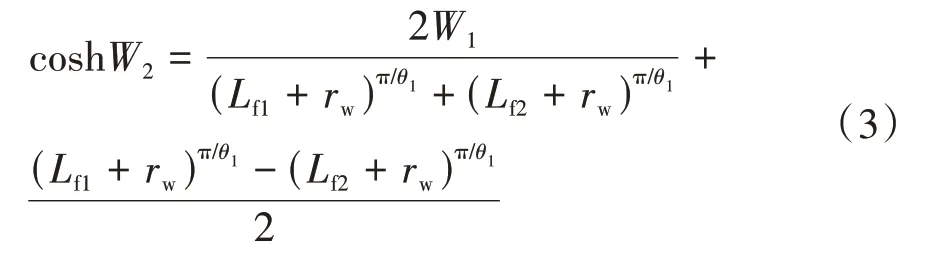
式中：Lf1——下部半缝长度，cm；Lf2——上部半缝长度，cm；rw——井半径，cm；下标f 表示裂缝；

1，2 表示下部和上部半缝；w 表示井筒。

变换后的地层长和宽分别为ξe和π，其具有长度特征，单位可视为单位长度。对其他半缝间地层，可作同样变换得到矩形地层。保角变换结束后，以单区为研究对象，进行产能评价。

2.1 外部渗流区

根据保角变换后流线变化特征，外部区域流动可视为单向流，如图1（f），由于流体流动达到拟稳态，建立的连续性方程为

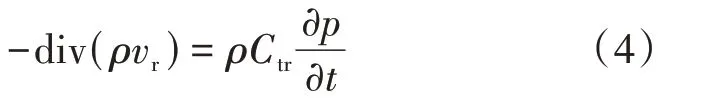
式中：ρ——原油密度，g/cm3；v——原油渗流速度，cm/s；p——压力，MPa；Ct——综合压缩系数，MPa−1；t——时间，s；下标r 为天然油藏区。

考虑应力敏感效应，运动方程为

式中：μ——地下原油黏度，mPa∙s；K——渗透率，μm2；α——应力敏感系数，MPa−1；ξ——保角变换后横坐标，cm；下标i 为初始条件。

内外边界条件公式为

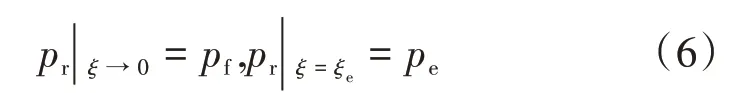
式中ξe——保角变换后横坐标边界，cm。

由式（4）和式（5）可得到

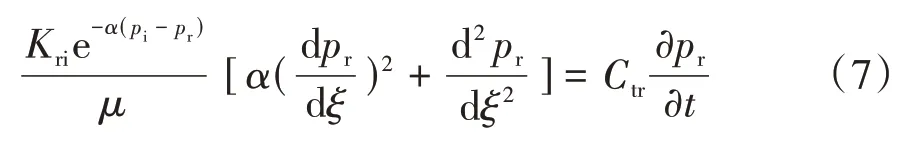
其中，在保角变换后坐标中，拟稳态状态下压力随时间变换为

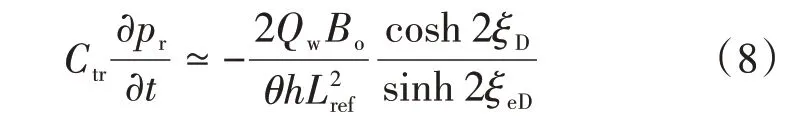
式中：Qw——油井产量，cm3/s；Bo——原油体积系数，cm3/cm3；Lref——参考长度，cm；h——油层高度，cm；下标ref 表示参考值，D表示所有量纲归一化。

根据量纲归一化参数，外部区域渗流方程为

式（9）和式（10）构成了拟稳态时的渗流模型，由于应力敏感系数的存在，方程系数具有强非线性。于是，采用Pedrosa 扰动方法［24‐25］进行处理。Pedrosa 扰动表达式可写为

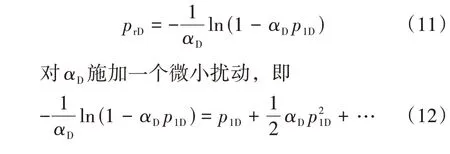
考虑到αD值较小，零阶扰动解可满足要求。因此，利用p1D来代替prD，替代后的渗流模型为

pfeD的计算公式为

2.2 裂缝渗流区

2.2.1 下部裂缝

由于油井的存在，裂缝中流线存在突变，如图1（f）。于是，将裂缝压力分段求解。对于下部裂缝，当流体在裂缝中满足拟稳态渗流，考虑储层流体向裂缝的补给［26‐27］，控制方程可表示为

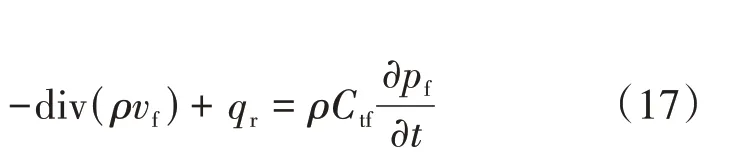
式中qr——地层流往裂缝的流量，cm3/s。

其中，考虑应力敏感效应，交换质量可表示为

式中bf——裂缝宽度，cm。

考虑裂缝渗透率的应力敏感效应，运动方程为

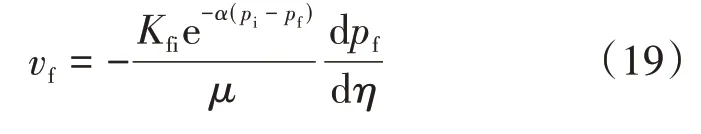
式中：vf——裂缝流体流速，cm/s；η——保角变换后纵坐标，cm。

内外边界条件表示为

考虑到油藏渗透率与裂缝渗透率比很小，忽略式（22）右端项，可得

式（22）和式（24）构成下部裂缝区拟稳态渗流模型。考虑到αD值较小，控制方程式（22）可简化为

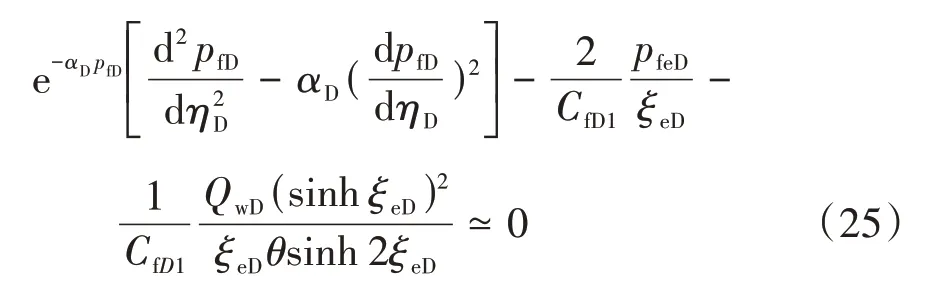
其中：pfeD=pfD−peD。同样由于应力敏感系数的存在，方程系数具有强非线性。于是，采用Pedrosa替代方法进行处理。Pedrosa 替代表达式为

代入边界条件式（28），可得

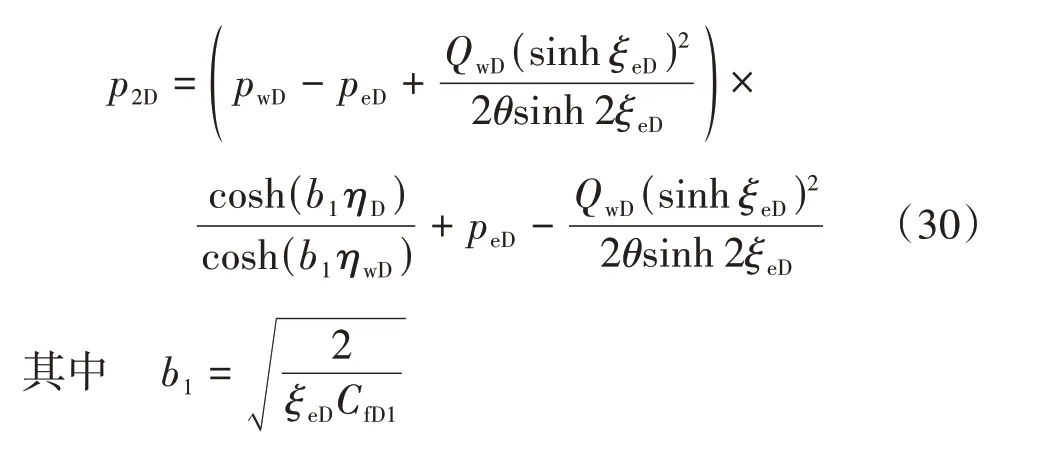
2.2.2 上部裂缝

上部裂缝区与下部裂缝区的渗流模型是类似的，仅边界条件存在差异。在裂缝中，流体流动的量纲归一化控制方程为

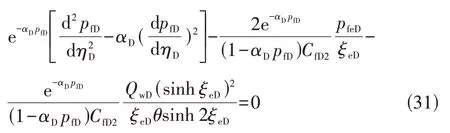
同样利用零阶扰动解p2D来代替pfD，控制方程可简化为

对此渗流模型进行求解，并代入边界条件式（33），可得

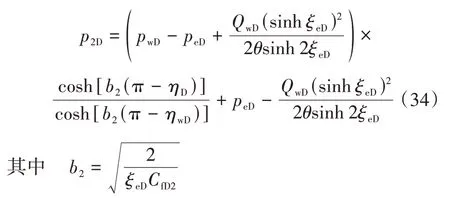
2.3 裂缝压力分布

根据渗流模型求解结果，p2D可用分段函数来表达，即

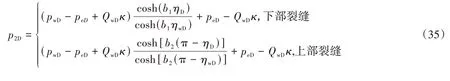
3 产能模型

3.1 单区产能模型

对于大型压裂直井，其产能可表达为

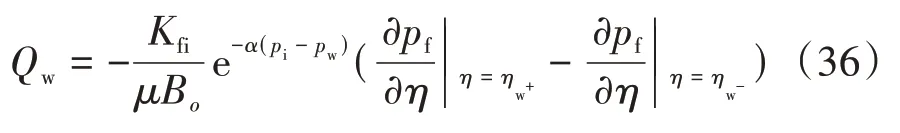
其中，上标+表示井筒上部方向，上标−表示井筒下部方向。量纲归一化后可表达为

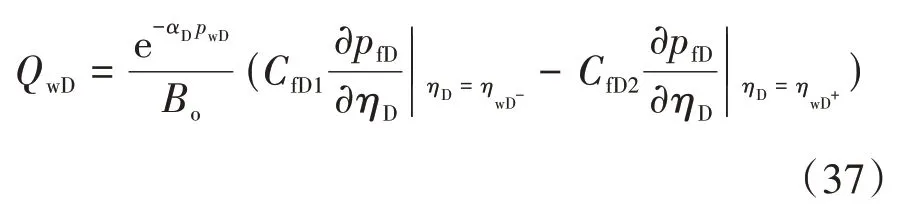
式中：CfD1——下部半缝的量纲归一化导流能力；CfD2——上部半缝的量纲归一化导流能力。

根据已求出的裂缝压力分布表达式（23），可得

式（39）即为单区地层对应油井产量的表达式。

3.2 整体产能模型

考虑裂缝长度，裂缝间夹角及裂缝导流能力的差异性，对于任意单区j可以表示为

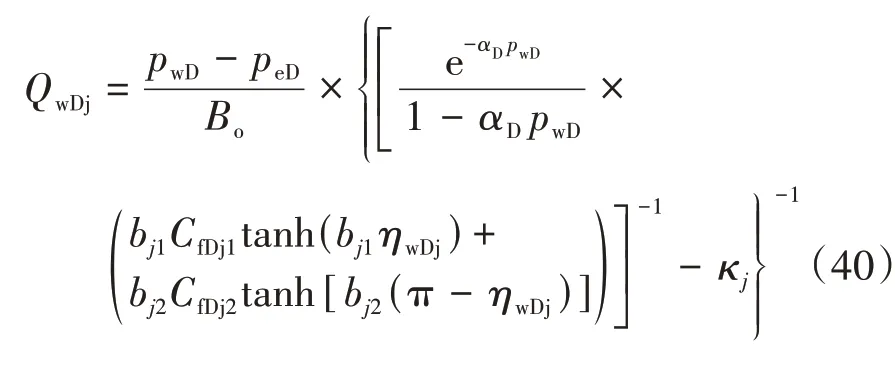
基于陈志明等［17］和Z.Chen 等［18］的产能叠加方法，忽略单区间影响，可得到考虑渗透率应力敏感效应和非圆形边界的大型压裂复杂裂缝直井渗流模型，公式为

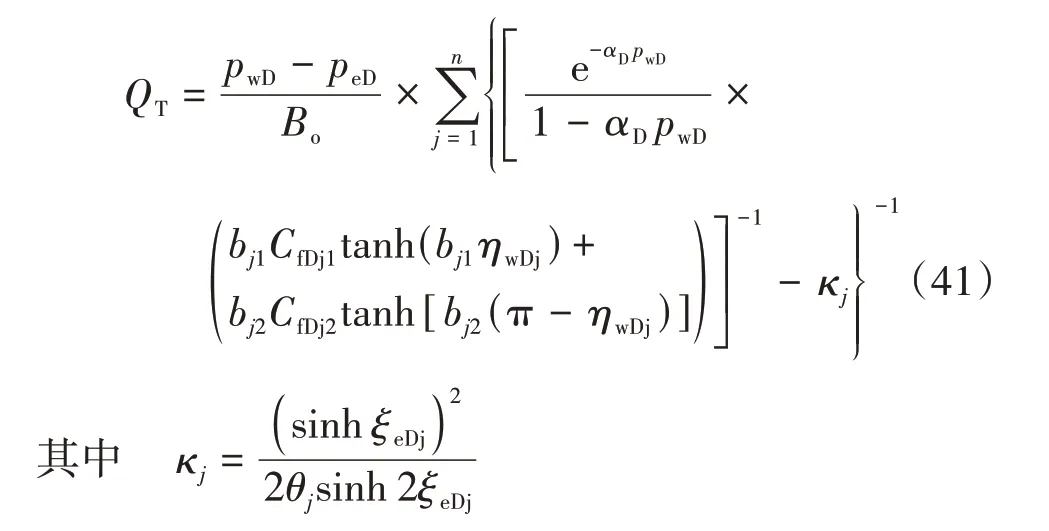
式（41）即为拟稳态产能模型，当然利用裂缝压力分布表达式（35）可得到平均压力与peD关系，则可得到关于平均压力与pwD的拟稳态产能公式。为便于理解，文中利用式（41）进行分析。

3.3 模型验证

3.3.1 解析方法验证

3.3.2 数值方法验证

利用商业数值模拟软件对建立的产能模型进一步验证。在数值模拟验证中，模型初始油层压力为30 MPa，油藏边长为313 m，控制面积为2.54×105m2，基岩渗透率为0.089×10−3μm2，孔隙度为6%，渗透率应力敏感系数为0.01 MPa−1，地下原油黏度为1 mPa ∙s， 原油体积系数为1.05 m3/m3。分别考虑了3 种不同缝网压裂井情况，裂缝基础数据见表1。利用式（41）计算产能前需进行渗透率单位转化。

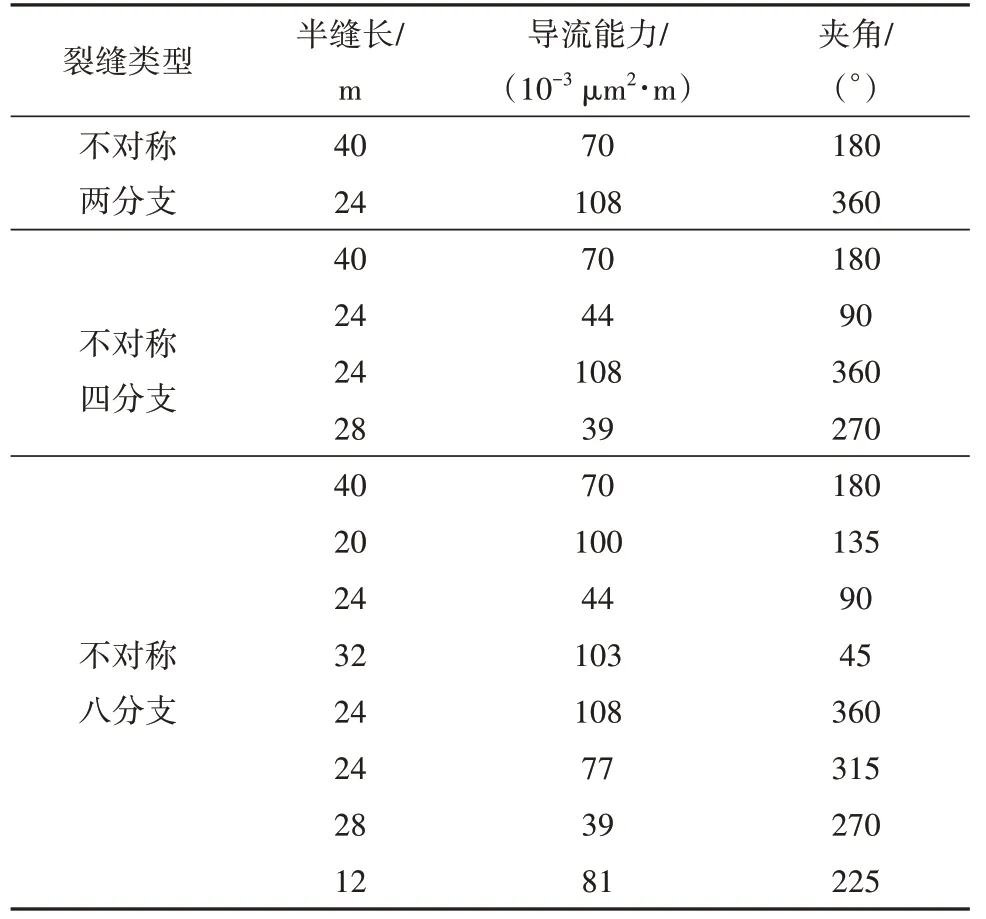
表1 裂缝网络参数Table 1 Parameters of fractures network

采用局部非结构化网格加密方式建立不对称两分支、四分支及八分支复杂裂缝数值模型（图2）。在不同油层厚度下，将式（38）计算结果与数值模拟结果进行对比，发现吻合程度较好，证明文中产能模型的可靠性（图3）。

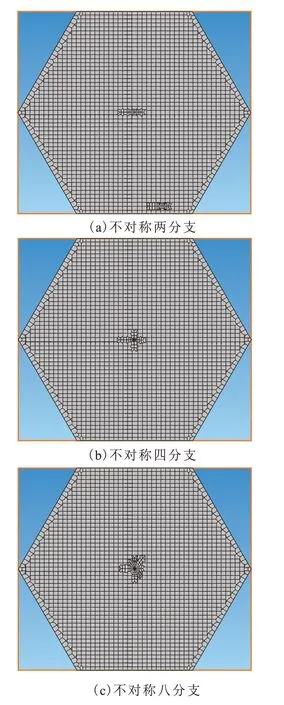
图2 非结构化网格复杂裂缝模型Fig.2 Non-structural grid models forcomplex fractures

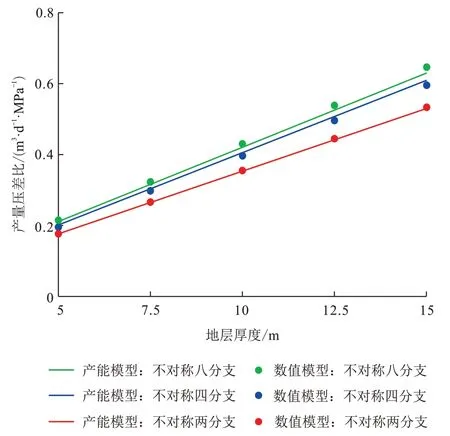
图3 不同储层厚度下大型压裂直井产量压差比的产能模型数值验证Fig.3 Numerical verification of productivity model for production-pressure difference ratio of LSF vertical well with different reservoir thickness

4 结果分析

基于某页岩油田WA 井参数，确定了理论模型部分参数：大型压裂直井裂缝分支数为6，初始油层压力为38.87 MPa，生产压差为27.00 MPa，油层厚度为8.95 m，油藏边长为697 m，控制面积为1.26 km2，基岩渗透率为0.089×10−3μm2，孔隙度为6%，渗透率应力敏感系数为1.5 GPa−1，地下原油黏度为1 mPa∙s，原油体积系数为1.05 m3/m3，裂缝基础数据见表2。

表2 裂缝基础参数Table 2 Basic parameters of fractures

4.1 渗透率应力敏感系数

基于表2 数据，获得大型压裂直井产能与渗透率应力敏感系数关系（图4（a））。随着应力敏感系数的增大，压裂井产能下降。这是由于随着应力敏感系数增大，基质渗透率下降速率增大，流体的渗流能力变小，因此油井产量下降。同时，由于渗透率下降幅度与应力敏感系数呈指数关系，因此压裂井产能与渗透率应力敏感系数也近似呈指数关系。

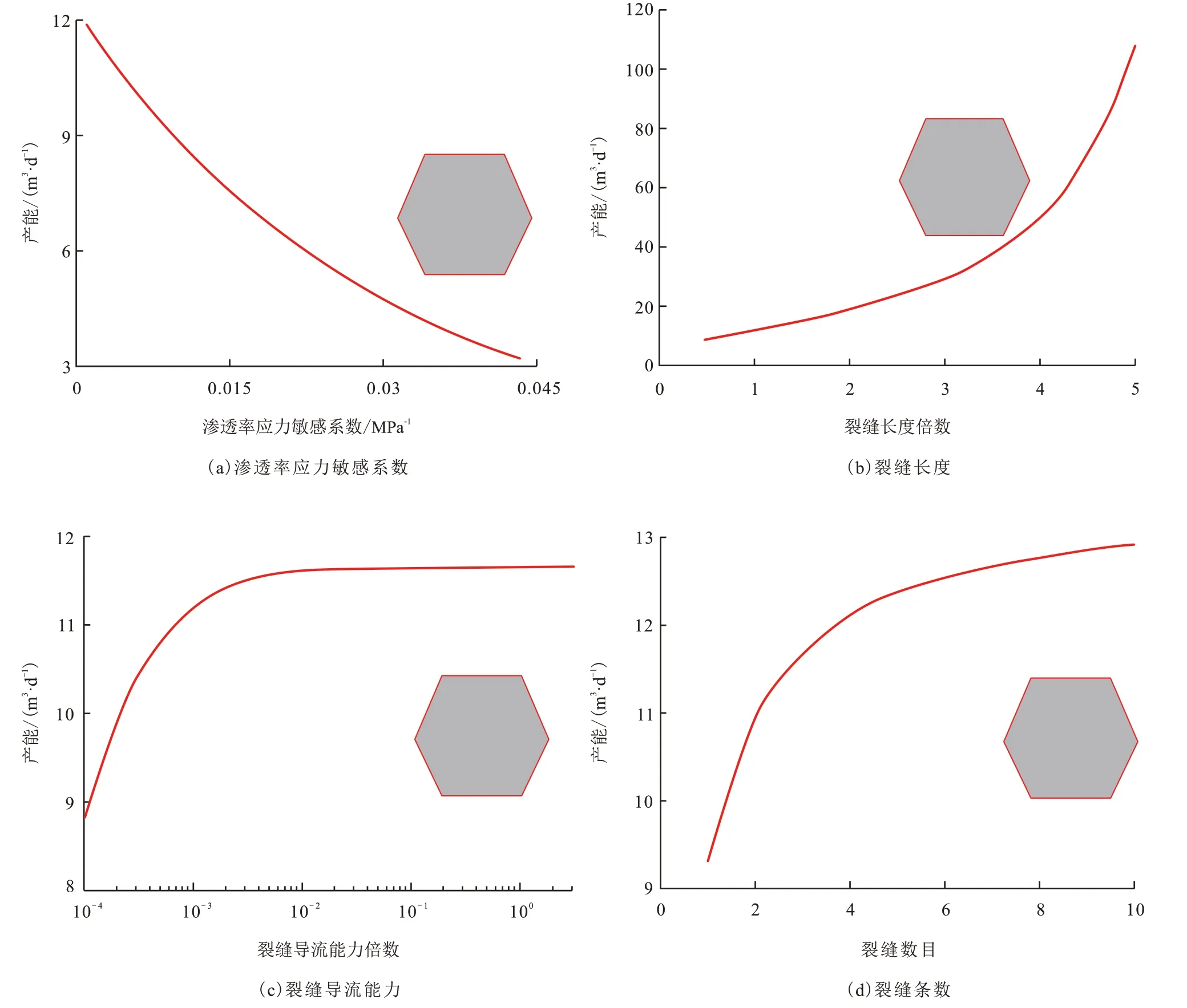
图4 大型压裂直井产能与各参数间关系Fig.4 Relations between productivity and different parameters of LSF vertical well

4.2 裂缝长度

基于表2 中裂缝基础数据，获得大型压裂直井产能与裂缝长度关系（图4（b）），其中各分支裂缝长度为等倍数变化。随着裂缝长度的增大，压裂井的产能增加，且随着长度倍数的增加，其对产能影响越明显。这是因为，随着裂缝长度增大，裂缝控制区域增加，流体渗流阻力减小，压裂井产能增大。当裂缝长度较小时，产能随长度变化较弱，裂缝导流能力对产能起主导作用；当裂缝长度较大时，裂缝长度起主导作用，产能随长度变化较明显。因此，在页岩油藏直井大型压裂时，建议尽量造长缝。

4.3 裂缝导流能力

基于表2 中裂缝基础数据，获得大型压裂直井产能与裂缝导流能力关系（图4（c））。随着裂缝导流能力倍数的增加，裂缝井产能增大，当裂缝导流能力倍数增大到0.1 后，压裂井产能基本保持不变。对于页岩油藏，当裂缝导流能力很大时，裂缝可近视为无限导流，继续增加其导流能力，对产能影响很微弱。同时，从产能模型也可看出，当裂缝导流能力很大时，式（41）中b值接近0，产能模型中裂缝导流能力参数可消去。因此，当裂缝导流能力增大到一定值时，导流能力的增加对压裂井产能影响很小。这与W.Luo 等［33］、S.Be‐rumen 等［34］和L.Wang 等［35］研究不对称压裂井试井模型时所得出的结论一致。因此，在页岩油藏压裂时，不必追求过高的裂缝导流能力。

4.4 裂缝数目

为分析裂缝数目对大型压裂直井产能的影响，假设裂缝是一致的，各裂缝半长和导流能力取表2中平均值为80.5 m，导流能力8.5×10−3μm2∙m，裂缝夹角60°，获得大型压裂直井产能与裂缝条数关系（图4（d））。由图4（d）可知，随着裂缝数目的增大，压裂井的产能增大，这是由于随着裂缝数目增大，缝控区域增大，流体渗流阻力下降，因此油井产能增大。当裂缝的数量增大到3—4 条时，增油量的幅度变缓。裂缝数量继续增大时，压裂井增油幅度减弱。究其原因，是因为随着裂缝数增大，裂缝间干扰程度会加剧，压裂井增油量的幅度减小。

5 应用实例

以鄂尔多斯盆地页岩油藏1 口大型压裂直井WA为例进行实例应用分析。油藏基本参数：泄流面积为1.54×104m2，初始油层压力为38.87 MPa，生产压差为25.40 MPa，油层厚度为8.95 m，基岩渗透率为0.089×10−3μm2，孔隙度为6%，渗透率应力敏感系数为0.01 MPa−1，泡点压力为10 MPa，地下原油黏度为1 mPa∙s，原油体积系数为1.05 m3/m3，井筒半径为0.1 m，裂缝分支数为6。大型压裂直井的其他详细参数见表3，图5 为该井的微地震数据。从微地震数据分析，该井压裂改造区近似为六面体。

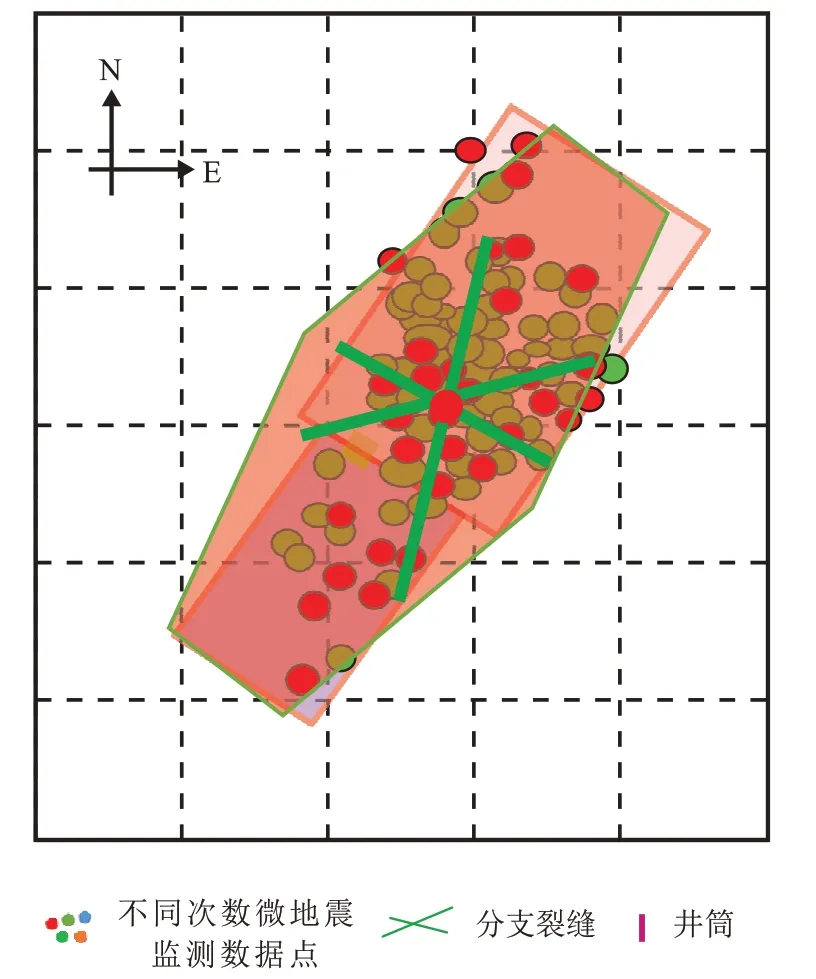
图5 鄂尔多斯盆地大型压裂页岩油井微地震点Fig.5 Microseismic spot of LSF shale oil well in Ordos Basin

表3 大型压裂直井的其他参数Table 3 Other parameters for LSF vertical well

采用式（41）来预测目前阶段选取的实际产量。同样，计算产能前需进行达西单位转化。分别考虑和不考虑应力敏感情况，与实际产能对比。结果发现考虑应力敏感效应预计的产量与实际产量平均误差为8.3%，基本符合大型压裂直井实际生产情况（图6）。

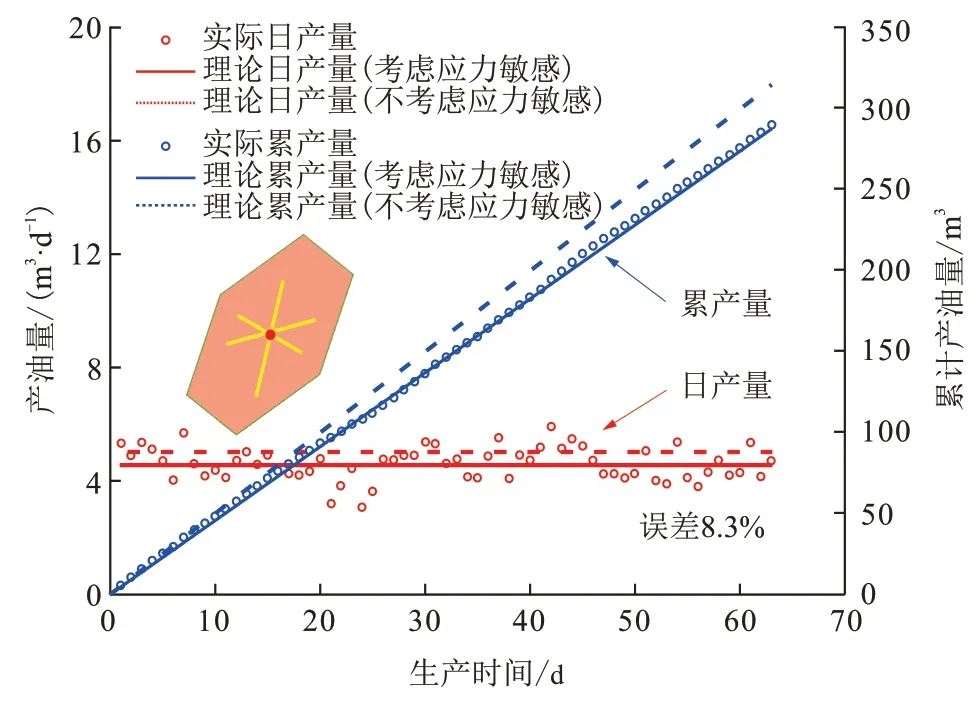
图6 大型压裂页岩油井的理论累计产量与实际累计产量Fig.6 Theoretical and actual cumulative productions for LSF shale oil well

6 结 论

（1）经过保角变换，本文的拟稳态产能模型与前人提出的典型裂缝井产能模型具有很好相容性，同时与数值模拟结果吻合程度较好，方程可靠性得到了验证。

（2）随着裂缝长度增大，裂缝控制区域增加，流体渗流阻力减小，压裂井产能增大。当裂缝长度较小时，产能随长度变化较弱，裂缝导流能力对产能起主导作用；当裂缝长度较大时，裂缝长度起主导作用，产能随长度变化较明显。因此，在页岩油藏直井大型压裂时，建议尽量造长缝。

（3）随着裂缝导流能力倍数的增加，裂缝井产能增大。对于页岩油藏，当裂缝导流能力很大时，裂缝可近视为无限导流，继续增加其导流能力，对产能影响很微弱。因此，在页岩油藏压裂时，不必追求过高的裂缝导流能力。

（4）随着裂缝数目的增大，裂缝井的产能增大，这是由于随着裂缝数目增大，缝控区域增大，流体渗流阻力下降，因此油井产能增大。裂缝数量继续增大时，裂缝间干扰程度会加剧，压裂井增油量的幅度减小。