电网电压不平衡下基于模块化多电平的高压直流输电控制策略

陈海燕, 程启明, 韩湘弘, 赵淼圳

(上海电力大学 自动化工程学院, 上海 200090)

模块化多电平变流器(Modular Multilevel Converter,MMC)的拓扑结构最早由一名国外研发人员提出[1]。MMC由若干结构相同的子模块(Sub-Module,SM)构成,能够非常便捷地实现扩展,具有广阔的工程应用前景。随着我国经济飞速发展,为缓解供电压力,各地都增设了直流输电工程。如上海南汇风电场输电工程、厦门柔性直流输电工程、鲁西背靠背直流异步联网输电工程等[2]。由于柔性直流输电与其他直流输电方式相比不会发生逆变站换相失败[3],且具有独立同步调节有功和无功的特点,使其越发受到关注。柔性直流输电技术不仅在电力系统正常运行时表现出优良特性,并且在交流系统发生故障导致电网电压不平衡时,仍具有较好的暂态特性,保证了其可靠的故障穿越能力。

基于电压源型换流器(Voltage Source Converter,VSC)的高压直流输电由来已久,其突出的技术优势已经展现出广阔的工程应用前景[4],引起世界各国研究者的关注。传统电力传输过程中都采用2电平拓扑的VSC元件作为输电系统的核心。这种变流器件中开关管数目少,采用脉宽调制(Pulse Width Modulation,PWM)策略也比较实用,但随着输电系统不断扩容,其开关频率高、开关损耗大等问题直接导致了效率降低,并且串联方式对器件的运行特性要求很高,高精度的控制必然增加成本,因此有了多电平器件的出现。VSC具有多种拓扑结构,如2电平、3电平、多电平等,本文的研究对象MMC就是多电平电压源型换流器的一种[5]。

柔性高压直流(High Voltage Direct Current,HVDC)输电系统的控制包括3个不同优先等级的环节:系统级、变流站级和阀级[6]。其中:系统级的控制逻辑级别最高,将收到的调度信号转化后发送到变流站;变流站级的控制是3者的核心部分;阀级的控制主要用来生成触发信号的调制控制,同时对MMC内部环流和子模块电容电压进行控制。系统两边的交流侧与两个不同的电力连接点相连,是非同步互联,两侧电网之间的功率交换可由MMC进行调节控制,因此其控制策略是维持系统安全稳定运行以及提高系统输电效率的核心技术[7-8]。

1 两端高压直流输电系统控制原理

首先需要建立MMC的数学模型,再分别对正常运行和不平衡故障下的控制策略进行研究。本文主要讨论变流站级的双环PI控制和阀级的环流抑制。双环PI的控制对象是MMC模型,环流抑制的控制对象是环流模型,由于篇幅所限且两者数学模型结构相似,即采用的控制方式也有共同点,所以本节只对变流站级的双环PI控制展开介绍。

1.1 正常工况下MMC-HVDC控制策略

在静止坐标下MMC的a相数学模型为

(1)

(2)

式中:La——a相等效电感;

idifa——a相内部环路电流;

Ra——a相线路电阻;

mp,mn——上、下桥臂调制电压的参考信号;

ucp——上桥臂电压;

icn——下桥臂电流;

Udc——直流侧电压;

iv——MMC的线电流;

Ua——a相输出电压。

由式(1)和式(2)可以得出变流器交流侧输入特性,交流电压源电压与输出相电压或桥臂输出电压之间的数学联系。

针对a相的公式可以直接类比到b相和c相,由此可得出基于静止坐标下的MMC数学模型,要想得到dq坐标系下的模型可以进行Park变换。

本文的研究对象是基于MMC两端背靠背高压直流输电系统。该系统由三相交流部分、直流输电线、整流站和逆变站等构成。本文所研究的相关控制方法都是为了使其能够安全高效地完成输电目标,符合工程应用实际的两端柔性高压直流系统。其系统结构如图1所示。

图1 两端柔性高压直流输电系统结构

借助有效的控制方式能使变流器输出电压可控,并能应对各种电压等级的需求。首先分析正常运行情况下的系统控制方式。对于任何控制系统而言,闭环控制都是不可或缺的,间接和直接电流控制通常进行双闭环矢量控制。图2为MMC换流站的控制结构框图。其中θ为锁相环输出相位角;Pref为有功功率的参考值;P为有功功率;Udcref为直流侧电压参考值,udc和idc为直流侧电压和电流;uabc和iabc为三相静止坐标下的电压与电流值;udq和idq为三相电压与电流的dq轴分量;udq_ref和idq_ref为电压与电流在dq坐标下的参考值;uabc_ref为三相静止坐标下的电流参考值。

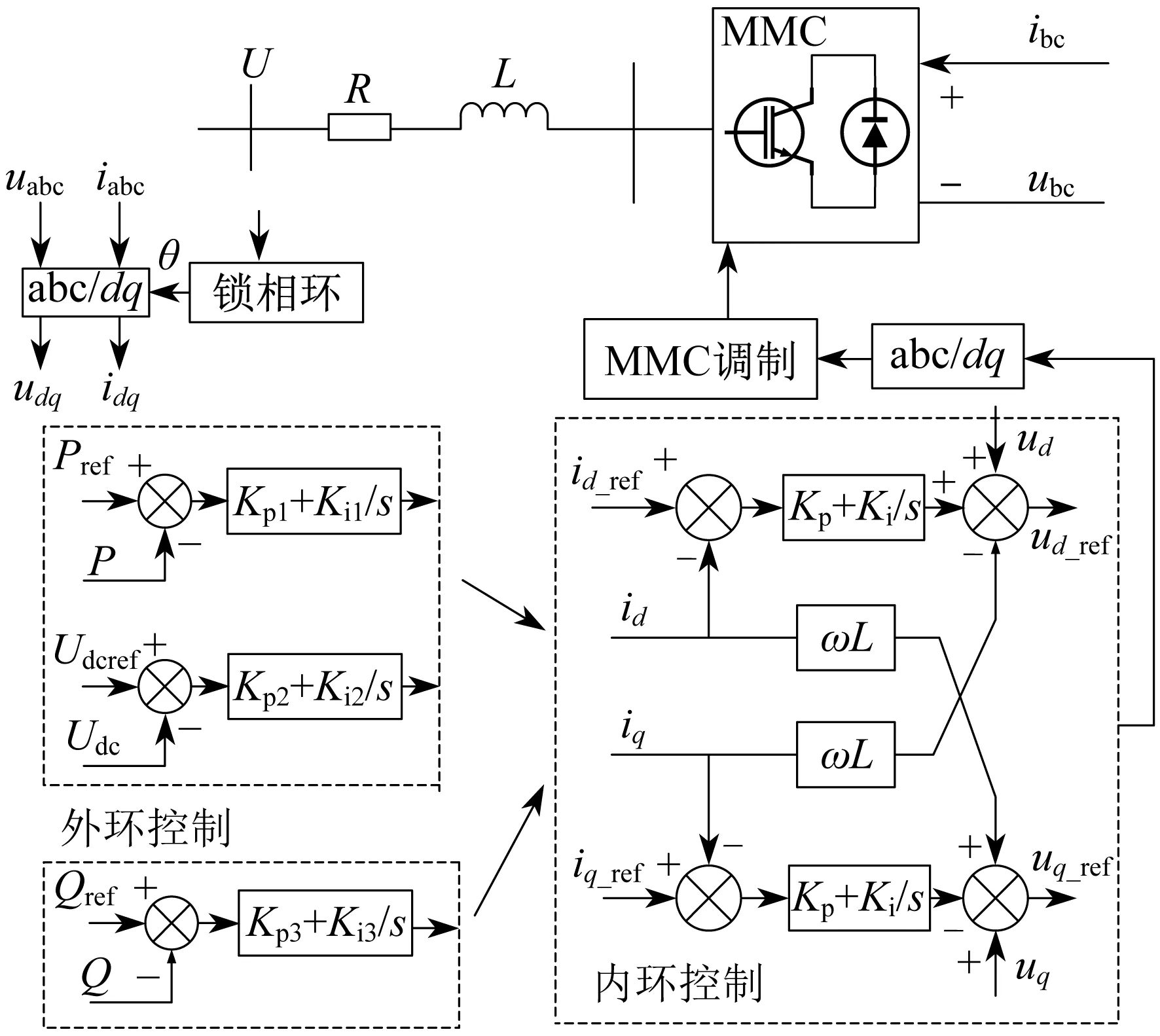
图2 MMC换流站的控制结构框图

内环控制引入电流负反馈,使得电流幅值和相位稳定在外环给出的参考值可以直接控制换流器电流。根据三相静止坐标下的模型,得到MMC在dq坐标系下的数学模型为

(3)

(4)

式中:L——等效电感;

isd,isq——MMC三相交流电流的d轴和q轴分量;

R——线路电阻;

usd,usq——MMC三相交流电压的d轴和q轴分量;

ud,uq——dq旋转坐标下d轴和q轴分量;

ω——电网基波角速度。

可以看出,MMC的各输入输出变量严重耦合。直流侧电压不变时,针对公式左边的一阶微分环节,可以用PI调节对桥臂电感上的电压降进行补偿。对于耦合环节需要附加解耦控制器实现解耦,还要一同引入电网电压前馈信号,改善系统旳动态性能。

1.2 电网电压不平衡下MMC-HVDC控制策略

输电系统在实际工作时,电力变压器通常采用Y/Δ接法。当电网电压不平衡时,由于角接方式没有零序通路阻断零序电流的流动,系统内部不会受零序分量的影响,因此故障时可以认为仅存在正负序电压电流分量。交流侧发生故障时,针对MMC的控制算法复杂度更高,通常设计以下控制逻辑在不平衡情况下对MMC施加合理控制,针对各序不同的特点考虑对各序独立控制。首先,要对电气信号进行正负序分离以便于分别施加控制逻辑。考虑到变压器一侧角接时零序电流不存在,不再单独设计零序控制。值得注意的是,相序分离时,响应速率会影响系统运行,所以要求相序分离逻辑控制精准迅速。其次,因系统不对称而出现的负序电流,可能导致器件过流,控制逻辑要能够有效抑制负序分量。控制逻辑如图3所示。

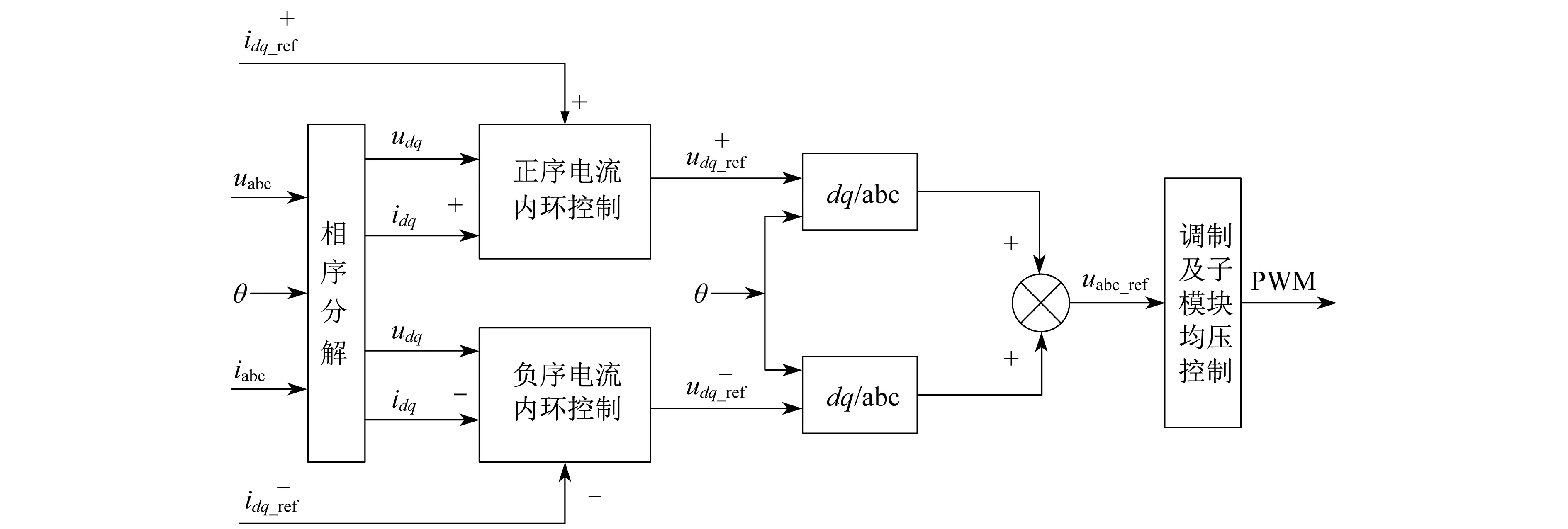
图3 不平衡下的MMC双序环控制

交流侧不平衡时的内环正序控制逻辑:输电系统在实际工作时,零序通路被阻断,只存在电压和电流正序分量,所以故障时的正序控制逻辑可以用正常运行时的控制逻辑替代。为解决因不对称故障出现的低次谐波,通过内环的比例矢量调节器来减小占比最高的谐波分量。

交流侧不平衡时的内环负序控制逻辑:针对负序的设计思路和正序相似,因为正序和负序模型结构相似,叠加得到的不平衡下的分相序内环控制模型如图4所示。

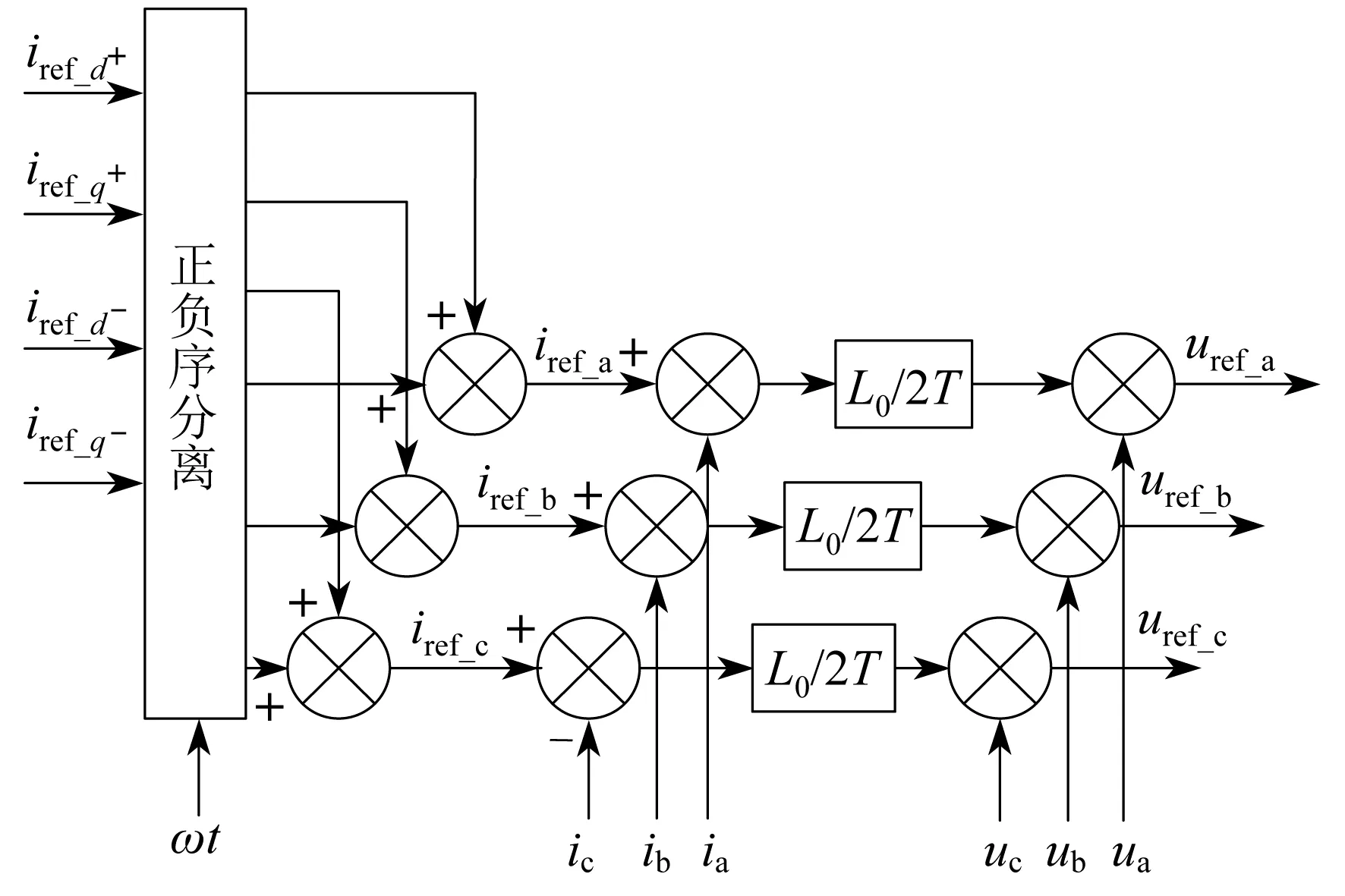
图4 不平衡下的分相序内环控制模型

图4中,iref_a,iref_b,iref_c表示MMC输出电流的参考值,iref_d,iref_q表示d轴和q轴坐标系的参考值,Lo是桥臂电感,T是采样周期。

根据以上分析可以在MATLAB软件中建立Simulink仿真模型,对正常运行条件和不平衡下的控制策略进行仿真实验分析。

2 仿真实验分析

2.1 正常工况下的仿真分析

稳态运行仿真系统仿真运行至1 s前达到稳定状态,故交流侧电压、电流波形选取了1 s以后的波形。系统稳定运行时,交流侧三相电压与电流波形如图5所示。系统稳定运行,直流侧电压波形如图6所示,仿真系统0.5 s后接近稳定状态,波形只有小范围波动,证明控制效果良好。

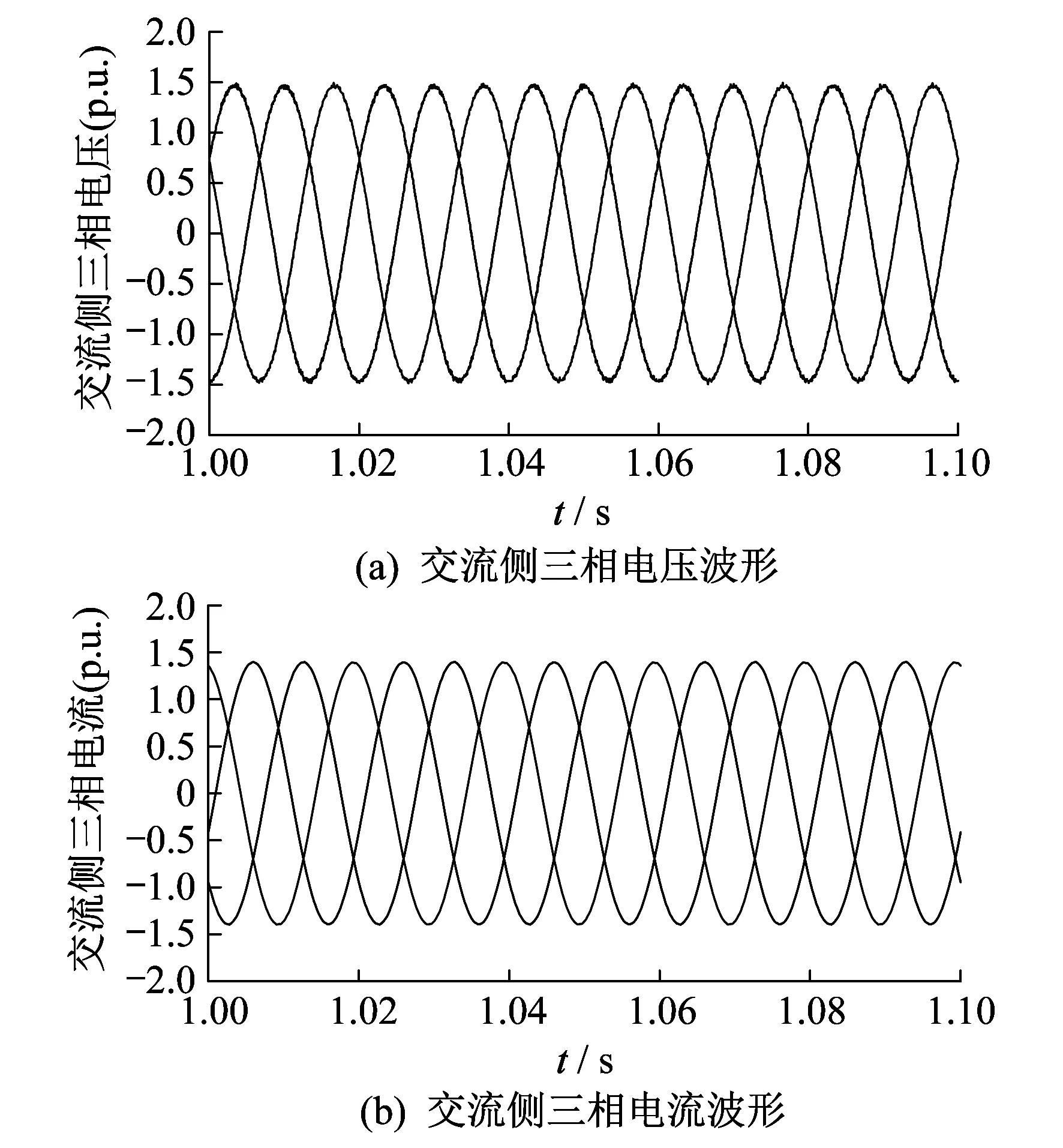
图5 正常工况下交流侧三相电压和电流

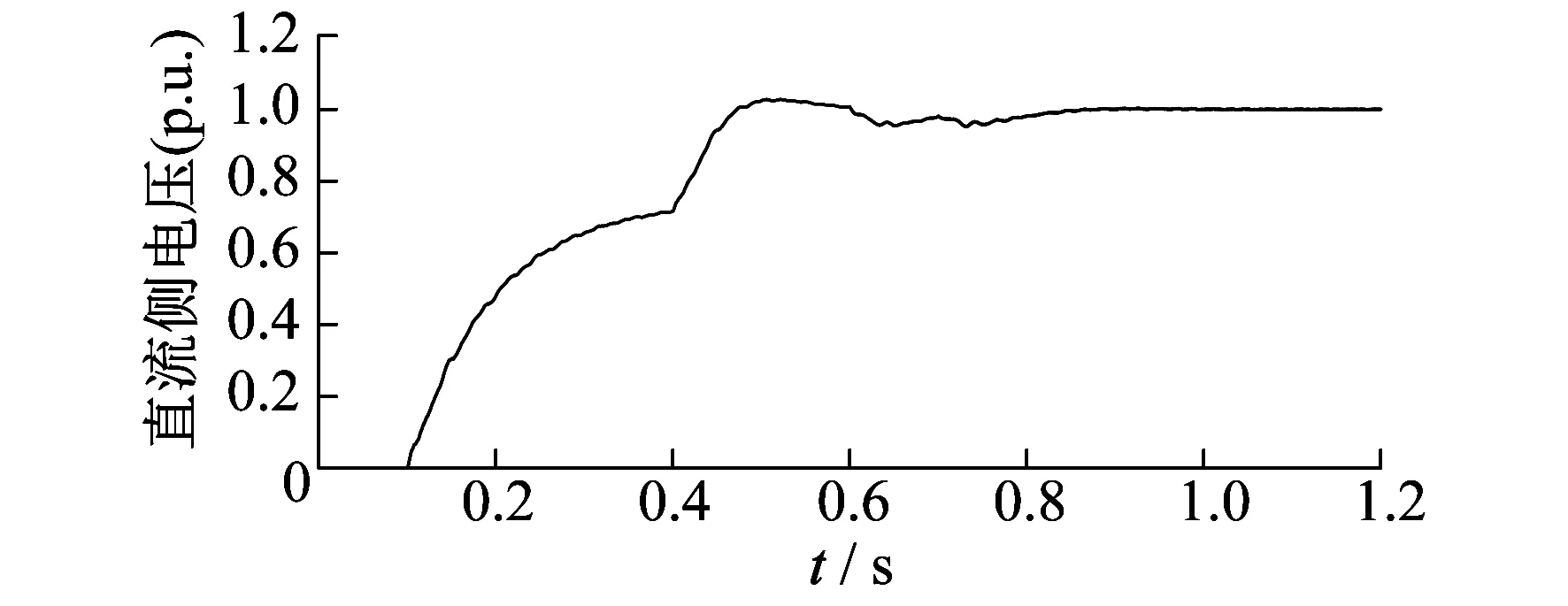
图6 正常工况下直流侧电压波形

图7为逆变侧环流波形示意。以逆变侧a相环流波形为例,在1.6 s投入环流抑制逻辑,能够消除二次谐波,使得环流的幅值有所降低且整体上表现极其接近正弦波,此时振荡能够被充分抑制。

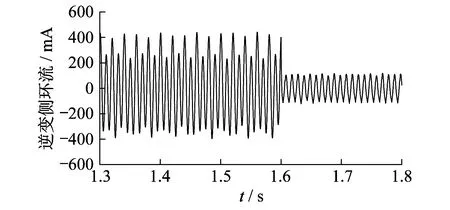
图7 正常工况下逆变侧环流波形示意

2.2 电网电压不平衡下仿真分析

图8为直流侧电压波形。发生接地故障时,直流输出电压在定直流电压控制下保持稳定。

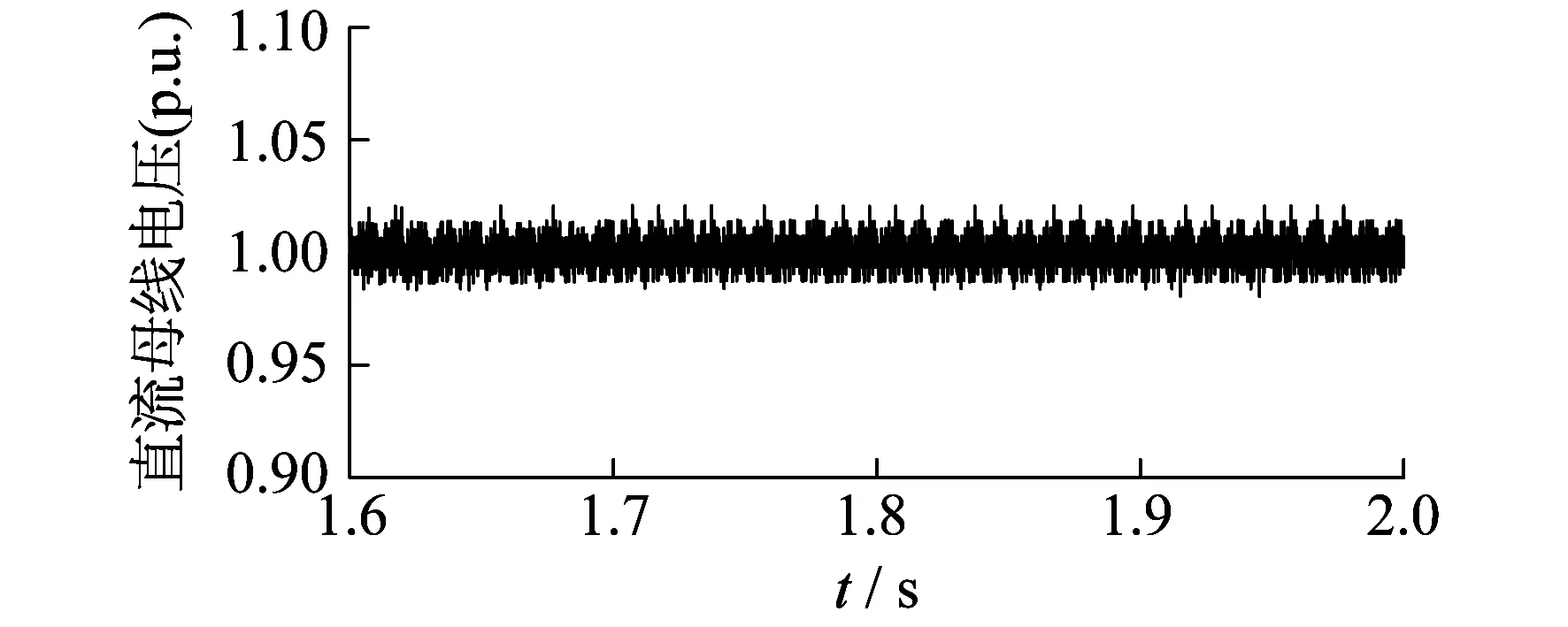
图8 电网电压不平衡下直流侧电压波形

图9为逆变器a相上桥臂的子模块电容电压波形。由于直流电压出现波动,所以电容电压也有振荡现象,但启动环流抑制器后电压波动得到抑制。

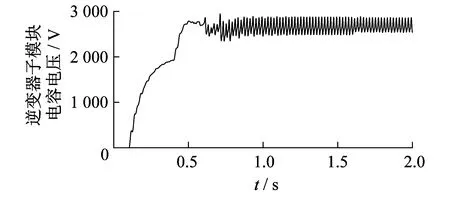
图9 电网电压不平衡下逆变器a相上桥臂子模块电容电压波形

3 结 语

本文针对MMC 的载波移相调制方法、子模块均压策略、MMC桥臂环流抑制策略以及双闭环控制等问题进行了分析与研究。探究了MMC及其半桥型子模块的拓扑结构,据此对MMC基本运行原理进行了论证,推导出静止坐标系下的数学模型,解决了子模块均压和桥臂环流抑制问题。在载波调制基础上对MMC-HVDC系统的控制进行研究,保证电网正常运行时MMC-HVDC能够安全稳定运行,并达到谐波含量少、高效可靠的输送效果。交流侧电网电压不对称,需要相序分离后设计电流内环和功率外环控制逻辑。仿真结果表明,在交流侧故障情况下系统仍然三相对称,控制器能够很好地抑制交流负序分量,防止换流器脱网。

本文研究对象为两端系统,如果将变流器增加到3个或3个以上则成为多端系统,此时电能传输需要经过多个MMC,控制机理也会发生变化。实际生产过程中的电力传输常常涉及故障处理问题,本文进行交流侧不对称故障分析时针对其幅值波动进行了研究,没有考虑相角不平衡等情况。

本文仅采用半桥结构子模块进行研究,根据实际目标不同可采用全桥等其他结构的子模块开展研究。