基于特征价格模型的中小城市住宅价格因素研究
——以泰州为例
刘 娟 张兆丰 杨志坚
(1.南京工业大学浦江学院,江苏南京 211100;2.辽宁出版集团有限公司,辽宁沈阳 110003;3.北方国家版权交易中心有限公司,辽宁大连 116600)
1 研究背景
21世纪房地产业发展迅速,影响住宅价格的因素逐渐变得复杂多样,其影响因素除住宅自身的建筑属性外,还包括周边基础设施、地理区位条件等。有多名学者对大型城市住宅价格的影响因素进行研究。张冕[1]对上海住宅价格进行分析,发现行政区、环线位置、轨道交通对住宅价格的影响超过70%,装修程度、绿化、周边教育对住宅价格的影响不如预期显著。乐建明[2]研究发现,南昌住宅价格与发现楼龄、住宅面积、地铁站距离、CBD距离、水体距离、卫生间数量、装修、停车位、公交线路条数显著相关。公共资源直接影响住宅价格。居住选址成为居民获得教育、医疗、交通等地方公共资源的中间机制,住房市场发挥城市公共资源空间配置的重要功能[3]。
江苏省三级甲等医院分布如图1所示。
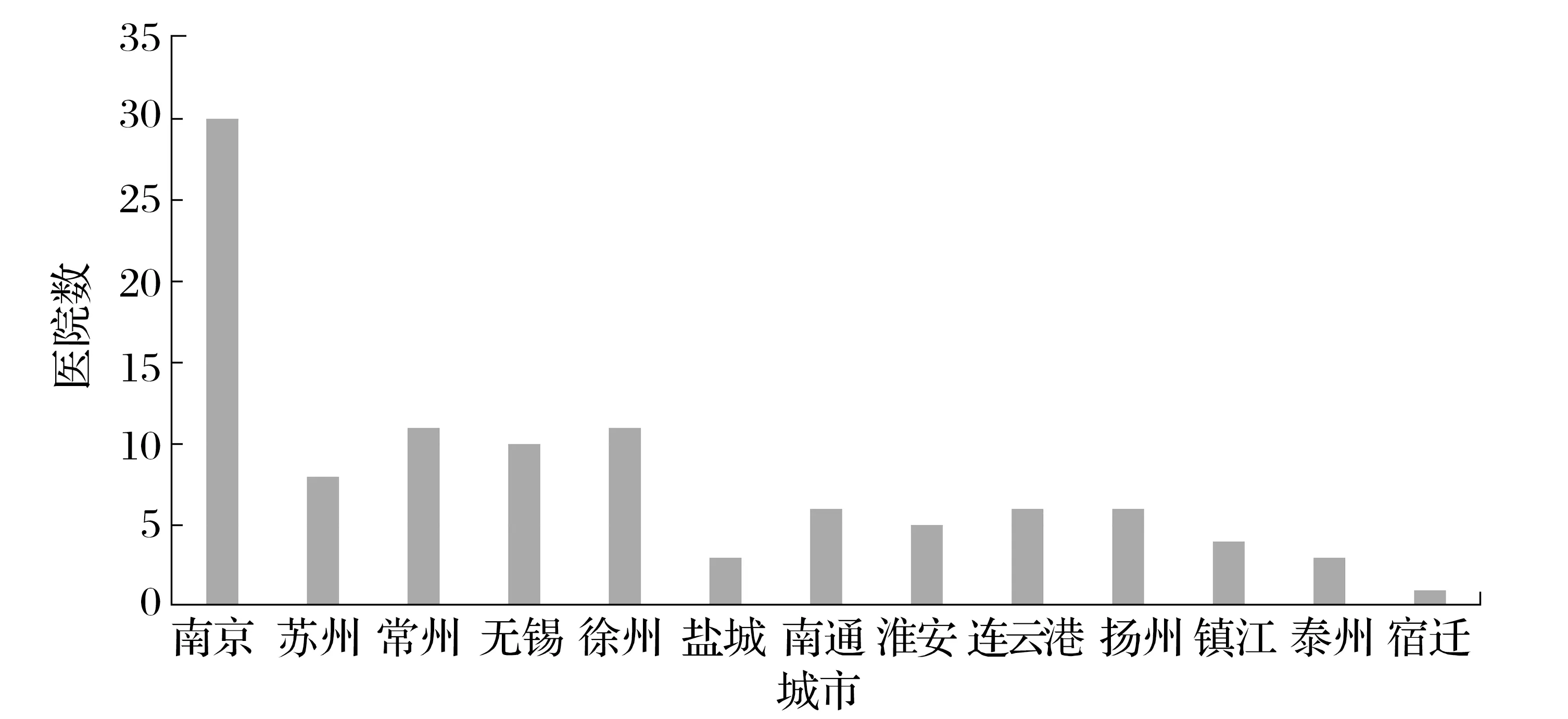
图1 江苏省三级甲等医院分布
针对体量最多的中小型城市,其在公共资源方面与大型城市具有显著区别。以医疗资源为例,江苏省三甲医院共104家,南京30家,占比28.8%;宿迁仅设置一家三甲医,医疗资源在不同城市间的分布极不均衡。以教育资源为例,在非官方的中国小学500强评定中,北上广深分别为62、50、31、21所,合计占比33.2%,大型城市占据绝大多数的公共资源,中小型城市的资源相对稀缺。中小型城市与大型城市在公共资源方面存在显著区别,中小型城市中居民对住宅的各项属性优先偏好度是否与大型城市不同,目前缺少此方面的研究。本文研究中小型城市的住宅价格,以泰州为例,探索中小型城市住宅价格的影响因素,为中小型城市购买住宅人群提供参考。
2 研究方法
2.1 特征价格模型理论
本文采用特征价格模型,方法基于美国学者Rosen提出的供求均衡模型,是一种用于分析处理异质商品差异特征与商品价格关系的模型[4]。
住宅是一系列给予消费者效用的集合,使用效用的满足程度取决于其内在特征的质与量。因此,住宅产品价格由与该产品特征的质与量相对应的多种价格组成。反映住宅特征质与量的一系列价格被称为特征价格。住宅特征价格模型在选定特征价格方程基础上,对搜集的包含住宅价格与特征因素的数据样本进行多元回归分析,对住宅所有特征属性进行定价,即住宅的特征价格系数。
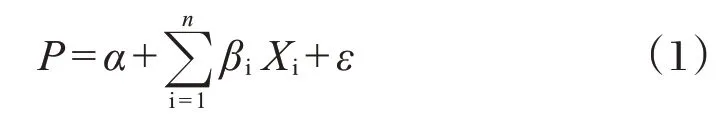
式中;P——住宅销售价格;βi——住宅特征属性的价格;Xi——住宅特征属性。
特征价格模型主要分为线性模型、对数模型以及半对数模型[5]。对数模型要求自变量不能为0,研究设置自变量时采用(0,1)二元虚拟变量,线性模型相更直观,因此本文采用线性模型进行估计,考察各变量对住宅销售价格的影响。
2.2 模型检验
(1)经济意义检验。模型结果要求经济意义和事实相符,若模型中出现多个符号错误,表示该模型具有偏差,需要重新进行调整。
(2)统计检验。统计检验要求模型的估计结果在统计学上具有意义,可以合理解释客观现象,需要进行拟合优度、回归参数的显著性、总体显著性检验[6]。
(3)计量经济学检验。计量经济学检验包括异方差性检验、多重共线性检验、自相关检验。多重共线性检验可以用方差膨胀因子即VIF检验,VIF大表明共线性强。自相关性利用D-W值检验,D-W值接近2表明自变量的自相关性不明显。
3 样本和数据
3.1 研究区域
泰州是江苏省辖地级市,位于长江三角洲中心区。截至2018年,全市下辖3个区、代管3个县级市,总面积5 787 km2,区域内优质的教育资源和医疗资源不多。
3.2 样本对象的选择
数据从安居客内部网站收集,2019、2020年住宅销售价格波动较小,2021年住宅销售价格波动较大,为减少整体市场对住宅销售价格的影响,选择2019年1月—2020年12月的销售数据,涉及区域为海陵区。住宅到市中心以及三甲医院的距离用百度地图测绘,小区周边特征通过高德地图获取。销售房屋涵盖9个大型小区,共195个数据样本,每组住宅样本的数据观测值包含房屋销售单价、住宅面积、物业管理费等11种。
4 影响因素以及变量设定
4.1 影响因素
(1)建筑特征主要指住宅本身的属性,包括建筑面积、房龄、楼层、物业管理状况等。
住宅的建筑面积大,房屋的总价高,潜在购买群体数量低。因此,建筑面积越大,单价越低。住宅建成的时间早,房屋售价低。
将住宅楼层分成低层、中层、高层,一般楼层越高,房屋售价越高。
物业服务的质量决定住宅居住环境,物业服务优质,物业价格高,住宅的价格也高。
按照装修程度分为精装、简装、毛坯。精装的住宅价格比简装高,简装的比毛坯高。
(2)周边特征主要指住宅周边的环境,包括生活配套设施、教育配套设施、医疗配套设施等。
生活配套设施全面,住宅销售价格高。
教育资源的质量是影响住宅价格的重要因素,配套优质教育资源的住宅销售价格高于一般住宅销售价格。
与医疗资源距离近,住宅销售价格高。
(3)区位特征主要指住宅在城市所处的地理位置,一般指距市中心的距离。距离市中心近,住宅销售价格高。
4.2 特征变量的选择
(1)采用特征变量的实际数值,该类特征变量包括住宅的面积、房龄、物业管理费、与最近三甲医院的直线距离、与市中心的直线距离。
(2)采用分等级赋值的形式,将特征变量的数值分为三个等级,对每个等级赋予(0、1、2)分值,特征变量包括楼层以及装修情况;
(3)采用二元虚拟变量进行量化,特征变量包括是否配套优质教育资源、最近1 km内是否有大型商场。
影响住宅价格的主要变量汇总如表1所示。
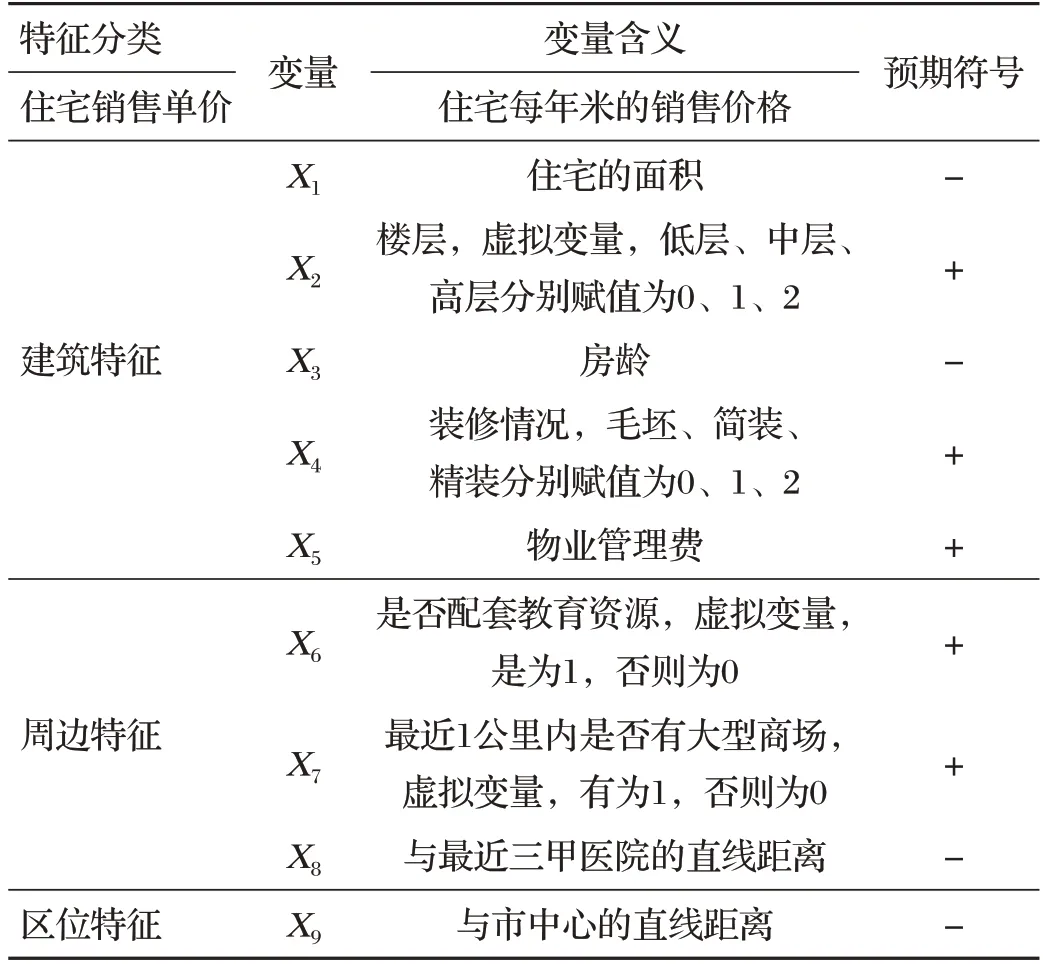
表1 影响住宅价格的主要变量汇总
5 回归分析与比较
5.1 样本的统计与描述
通过SPSS软件对整体样本共计195组数据进行分析,2019年数据占比46%,2020年数据占比54%。
具体描述汇总如表2所示。
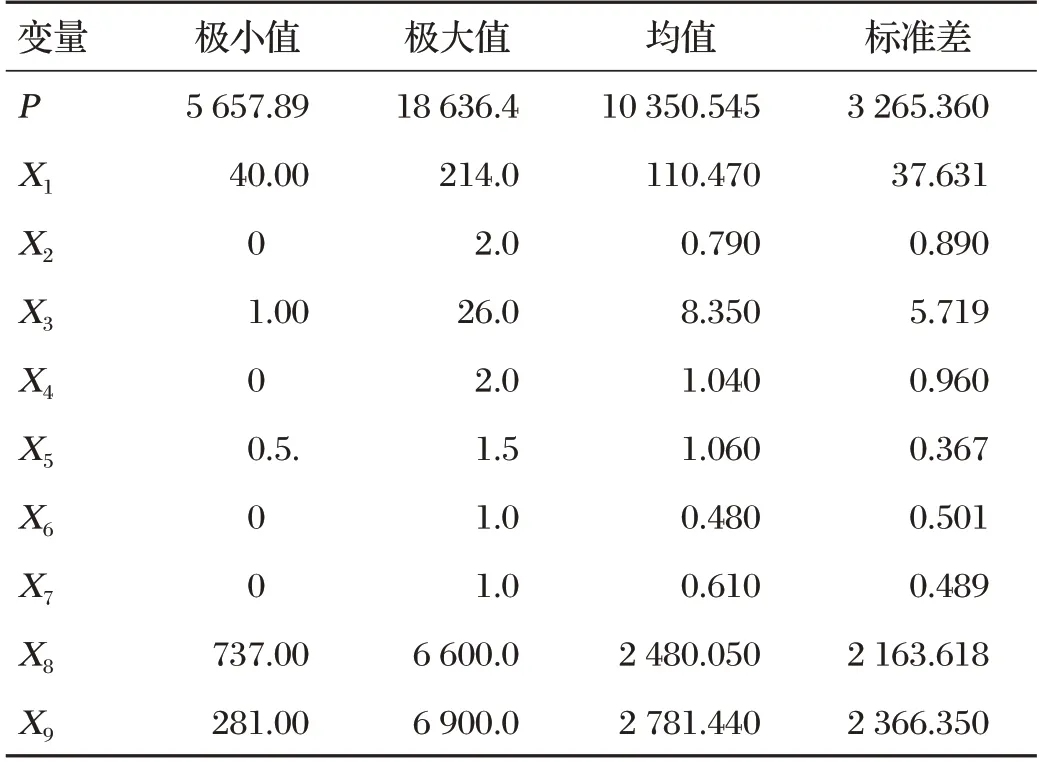
表2 样本描述性统计
5.2 模型的建立
根据线性模型建立公式:
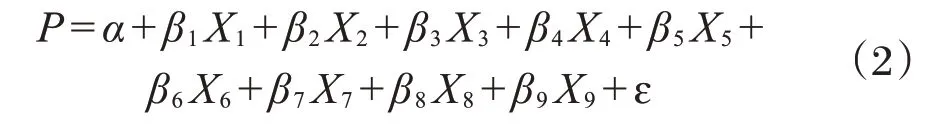
式中:P——住宅销售单价;α——除特征变量外其他影响价格的常量和;βi——特征变量与P相关系数;Xi——特征变量;ε——误差值。
5.3 显著性检验
在显著性检验中,模型R为0.929h,R2为0.864,调整R2为0.858,标准估计误差为1 230.630 54,D-W值为1.910,表明线性模型拟合度较好。
方差分析结果如表3所示。
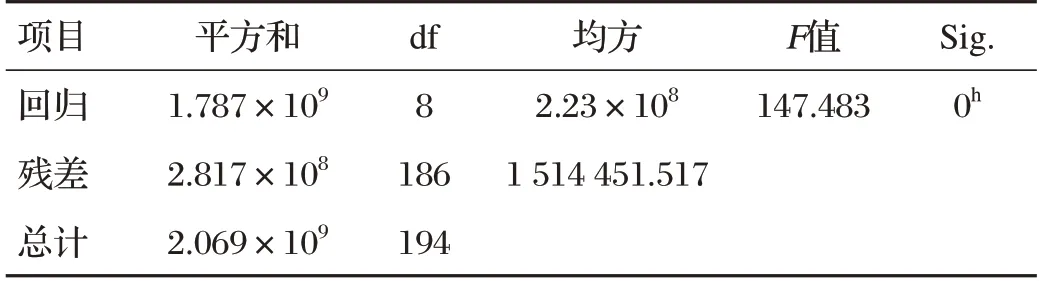
表3 方差分析结果
由表3可知,Sig接近0,通过T检验,结果通过显著性检验。
5.4 多重共线性检验
VIF小于10时,自变量间不存在共线性,否则存在共线性,本文VIF均小于10,表明模型通过多重共线性检验。
5.5 方差齐性检验
残差与预计值散点如图2所示。
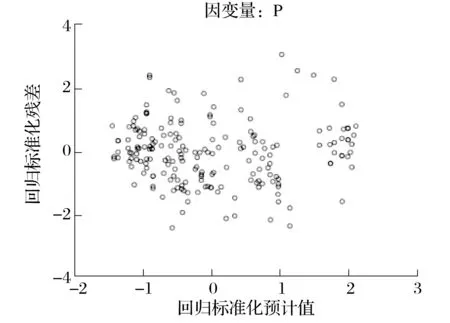
图2 残差与预计值散点
大部分数据落在-2~2区间时,模型满足方差齐性检验要求。结果表明,模型满足方差齐性检验。
5.6 D-W检验
D-W检验可以检验变量自相关性,D-W值接近2,自变量的自相关性不明显,本模型D-W值为1.910,说明自变量相关性不明显,满足检验要求。
5.7 残差的正态性检验
残差直方图如图3所示。
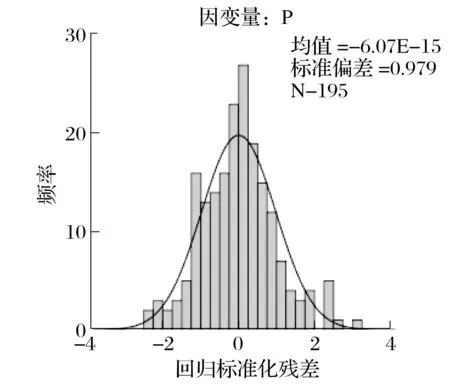
图3 残差直方图
概率散点图如图4所示。
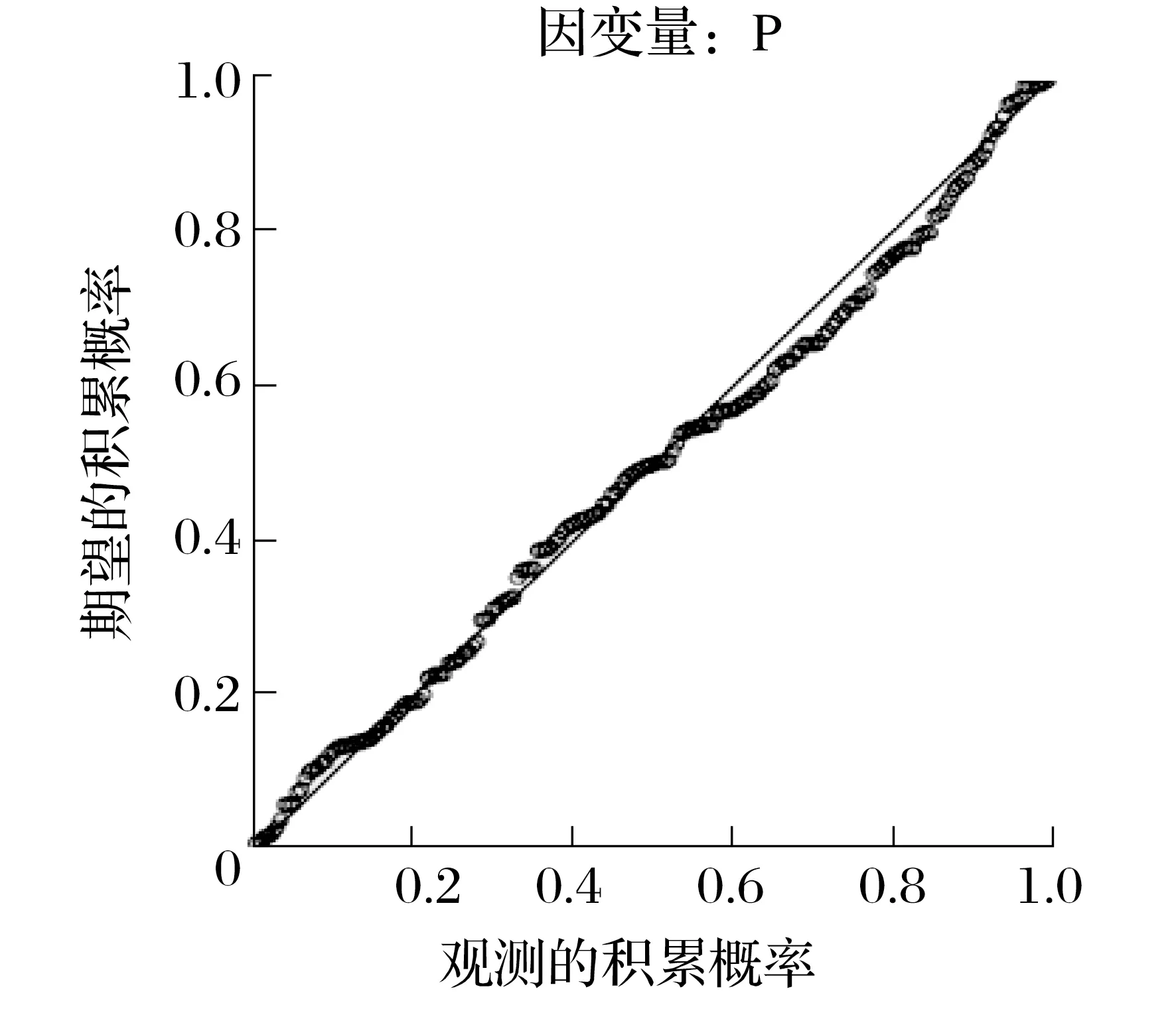
图4 概率散点图
由图4和图5可知,残差基本成正态分布,满足检验要求。
该线性模型在满足相关假设的前提下,具有良好的拟合度和较高的解释能力,具有统计学意义。
6 结果分析
通过SPSS逐步回归得到系数汇总表。
回归系数汇总如表4所示。
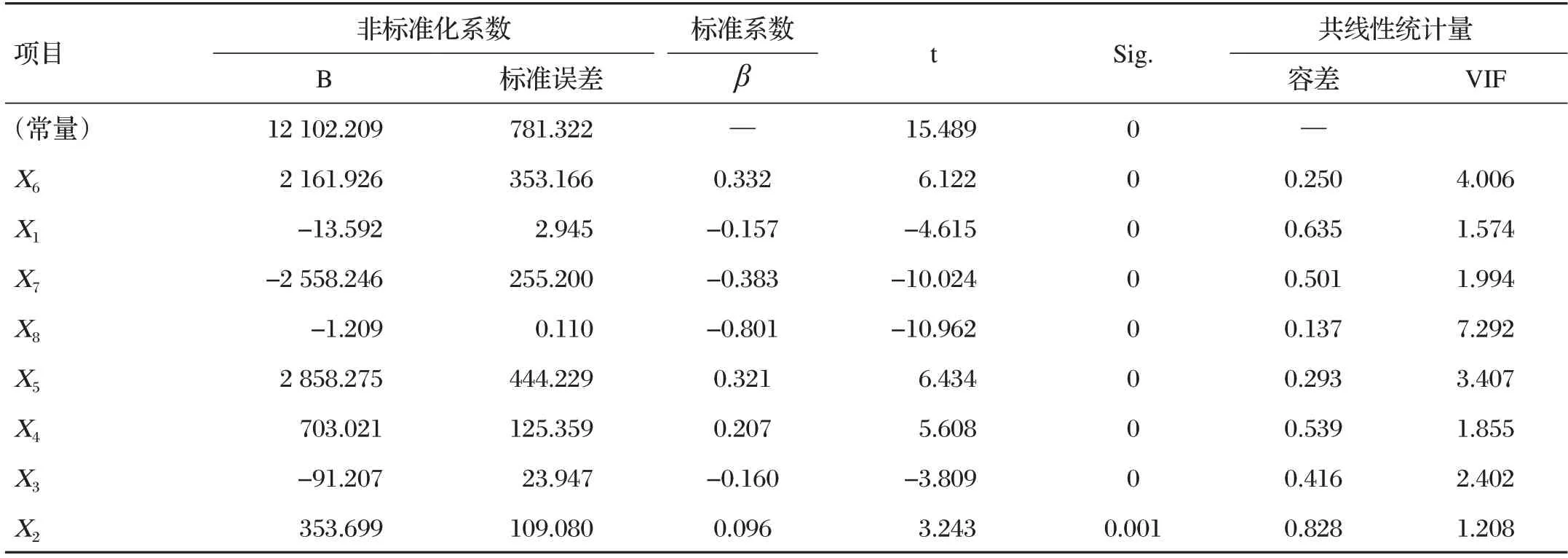
表4 回归系数汇总表
6.1 经济意义分析
8个自变量进入模型,即建筑面积、楼层、房龄、装修、物业价格、是否配套优质教育资源、1 km内是否有大型商场、与最近的三甲医院距离对住宅价格产生影响,与大型城市的结果相似,但在泰州市的数据分析中,与市中心的距离对住宅价格影响并不显著,可能因为家用汽车比较普遍,且中小型城市规模相对较小,交通方便。
在所有显著性变量中,1 km内是否有大型商场、建筑面积以及是否配套优质教育资源对住宅价格的贡献最大,楼层、房龄以及装修情况则对房价的影响最弱。
针对中小型城市,教育资源以及医疗资源对住宅价格产生重要影响,与大型城市相同,但是与CBD的距离影响大型城市住宅价格不同,在中小型城市中,教育资源以及医疗资源因素对房价的影响不如设想得显著。
6.2 边际价格分析
测算自变量对住宅价格的影响:
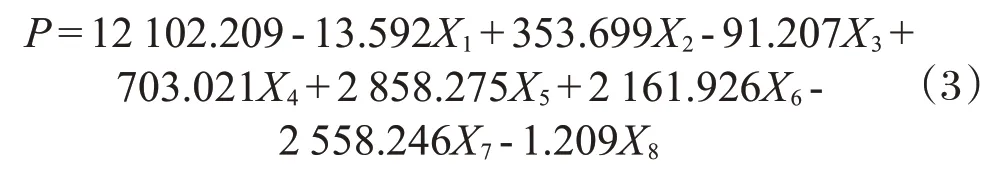
地区住宅增加1 m2,住宅销售单价下降13.592元;高层比中层以及中层比低层均价高353.699元;房龄每增加1年,住宅销售单价下降91.207元;精装比简装以及简装比毛坯销售价格平均高出703.021元;物业管理价格上升1元,住宅销售单价上涨2 858.275元;配套优质教育资源的住宅比普通住宅平均销售单价高出2 161.926元;1 km以内有大型商场比没有的销售单价低出2 558.246元;与三甲医院距离每增加1 m,住宅销售单价下降1.209元。
7 结语
本文运用特征价格模型研究泰州市住宅销售价格的影响因素,利用SPSS进行逐步回归发现,利用特征价格模型定量化计算影响住宅价格因素具备合理性。
通过模型运算得到,影响住宅价格的主要因素包括建筑面积、楼层、房龄、装修、物业价格、是否配套优质教育资源、1 km内是否有大型商场、与最近的三甲医院距离,为开发商的前期策划与定价提供依据,此外,模型对消费者具有有效的指导意义。但是研究仍存在一些不足,包括样本数据选取范围受限、变量选择不够全面,考虑在今后的研究中,扩大数据范围,选用更多的变量以及变换设计模型,使之具备更好的解释能力。

