基于Cox比例风险模型的山地城市快速路拥堵因素影响分析

白 桦 刘秀彩 曹 璐

（华设设计集团股份有限公司，江苏南京 210014）

城市经济快速发展和路面机动车数量激增，可能导致交通拥堵和安全问题。中国交通运输部研究数据指出，交通拥堵带来的经济损失占城市人口可支配收入的20%，将制约城市的发展和社会的进步，交通拥堵的成因、规律、影响因素成为各界学者关注的热点话题。Sun[1]通过收集分析交通拥堵指数及其相关特征，对某市商业区的拥堵现状、时间和原因等进行深入分析。Maria[2]提出从数据收集到指标计算的全流程多源数据融合框架，用于计算指定路段的流量。计寻[3]以极端天气中的暴雨天气为落脚点，研究暴雨发展的不同阶段对交通流产生的影响。Alsharari等[4]研究恶劣天气和事故造成的道路封锁对不同宽度道路通行能力的影响。常桃宁[5]分析拥堵的成因和危害，研究道路等级因素对交通拥堵的影响。潘雨诗等[6]以新能源汽车GPS数据为基础，建立基于车辆真实轨迹数据的交通拥堵指数模型，使交通管理控制策略的制定更精细化。现有研究主要围绕交通流量、运行速度、车道占有率等参数，剖析交通拥堵形成、传播规律，对拥堵持续时间的研究较少。本研究利用GPS浮动车数据、GIS平台和Python语言，提取交通路段拥堵持续时间参数，基于Cox比例风险回归模型定量剖析不同因素对重庆快速路拥堵持续时间的影响程度，探索影响拥堵的关键因素，为减少缓解交通拥堵提供参考。

1 Cox比例风险回归模型

1.1 Cox回归模型构建

Cox比例风险回归模型（Cox回归模型）可以分析不同因素对某种生存现象的影响程度，不需要考虑生存数据本身的分布形式、数据是否完全、数据是否缺失，可以同时探索多种因素对现象的持续影响力度。拥堵持续时间可以反映拥堵消散特征，易受外部多种因素影响，分布类型难以明确，判断拥堵持续时间与影响因素间的影响关系时，可以构建Cox回归模型进行分析。借助风险率反映影响因素对拥堵持续可能性的影响，确定拥堵是否会持续。

构建Cox回归模型时，采用基准危险函数h0(t)与相应协变量函数f(x)的乘积代表危险率函数h(t)。

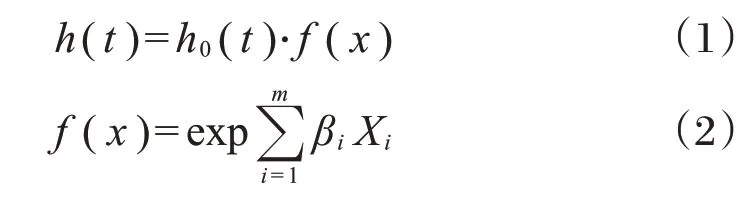
式中：x——拥堵的影响因素，如车道数、速度和流量等；t——某一时刻；h(t)——t时刻的拥堵持续概率。

在基准危险率函数分布类型不明确的情况下，Cox回归模型的参数跳过基准危险率，不直接解析生存函数S(t)与协变量的关系，利用风险函数h(t)作为因变量研判影响因素对生存函数的影响程度。

式中：h(t，X)——影响因素X的个体在时刻t的危险率；h0(t)——非参数部分，所有危险函数为0时的基础风险率；exp(β1X1+β2X2+···+βnXn)——参数部分；β=(β1，β2，···，βn)——偏回归系数，其他因素不发生变化时，X=(X1，···，Xn)可能影响生存时间的潜在影响因素。

1.2 影响系数估计和影响程度判断原则

（1）影响系数β估计。

计算生存函数S(t，X)与风险函数h(t，X)的关系：

推导影响因素X与生存函数的关系：

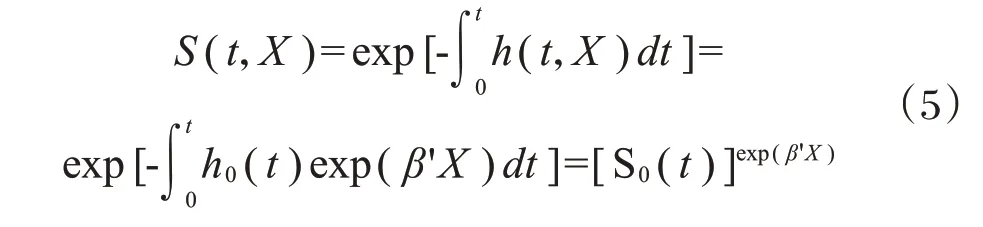
式中：S0(t)——影响因素全部为0时，拥堵持续时间超过t的概率。

各类因素对拥堵持续时长的影响取决于影响系数值β。利用偏似然函数估计β，计算基准风险率函数和风险函数，可以明确因素对拥堵消散的关联程度。

（2）影响因素与拥堵持续时间关系确定。

相对危险度RR表示影响因素X每增加一个影响单位时，拥堵降低持续的概率是原来的exp(βi)倍。

若β＜0、RR＜1，可以增大拥堵持续时间的生存概率，拥堵更易持续，是拥堵持续的保护因素；若β=0、RR=1，为交通拥堵的无关因素；若β＞0、RR＞1，可以降低拥堵持续时间的生存概率，拥堵不易持续，有利于拥堵消散。

2 拥堵影响因素Cox比例风险模型思路简介

本研究处理重庆市GPS浮动车数据，获取不同路段交通拥堵持续时间，研究标准化天气条件（雨天、非雨天）、交通状况（平均速度）、时间因素（双休日周末、早高峰、晚高峰、平峰时段）、道路条件（匝道、桥梁、车道数、公交站点）四类影响因素（共8种），借助Cox比例风险回归模型计算影响系数，结合影响系数的大小剖析各类影响因素对拥堵持续时间的影响程度。

模型构建流程如图1所示。

图1 模型构建流程

2.1 数据预处理

GPS浮动车数据记录车辆运行时刻、瞬时速度、位置等时空信息，可以高效准确地获取道路交通运行状况。GPS采集设备可能受外部因素影响，为精确提取路段交通拥堵持续时间参数，需要对GPS数据和路网进行处理：对坐标信息缺失、速度过大、时间戳错误等异常GPS数据进行清洗；采用合流分流原则对路网进行路段划分，借助GIS平台实现地图匹配，得到路段的交通运行状态；利用Python语言获取路段拥堵持续时间。

2.2 影响因素选取

交通系统中，任意因素均可能造成交通拥堵持续时间波动，不同影响因素下的交通规律不同。雨雾天气会影响行驶环境，降低路面可见度，交通安全系数低，极易造成交通拥堵；路段行程速度等交通参数的变化可以综合反映交通状态的演变过程，交通状况对路网交通状态的影响不可忽视；居民出行的目的和强度不同，高峰时段、平峰时段、工作日、周末等不同时间区间内，城市路网的交通运行具有差异性；车道数的变化、匝道及公交站点布设等道路条件的不合理设置均会影响道路的通行能力，造成交通的供需失衡，影响拥堵持续的概率。

3 案例分析

本文获取重庆市某快速路路段拥堵持续时间，综合考虑影响交通的天气条件、交通状况、时间因素、道路条件4类影响因素，构建山地城市拥堵持续时间的Cox比例风险回归模型。

公交站点的设置对通道交通拥堵影响不大；桥梁是山地城市快速通道的交通拥堵瓶颈，是造成交通拥堵影响最大因素，需要重点改善和管控，缓解交通拥堵压力；雨天、低速度、工作日、早高峰、晚高峰、桥梁、匝道、四车道容易减小拥堵结束的风险率，增大拥堵持续的生存率，产生长时间交通拥堵，与非雨天、高速度、周末、平峰时段、非桥梁路段、无匝道、三车道相比，拥堵持续的概率依次增加8.3%、2.7%、13.9%、14.9%、18.1%、50.2%、11.6%、9.4%。

Cox比例风险模型影响系数估计值如表1所示。

表1 Cox比例风险模型影响系数估计值

4 结语

交通系统易受多种因素干扰，在大数据环境下，构建可靠的交通分析模型可以定量测度影响拥堵持续时间的因素、影响方向和强度，为相关部门交通管控策略的制定提供量化依据。本文主要考虑交通拥堵持续时间的4类影响因素，在后续研究中，需进一步细化和分析影响拥堵持续时间的因素，与相关部门沟通获取大雾、大雪、交通事故等信息，从而更全面、准确地判定交通拥堵持续时间影响因素，为交通管控策略提供更加合理有效的决策依据。