基于隐马尔可夫模型的非侵入式负荷监测泛化性能改进

苏 晓,余 涛,徐伟枫,蓝超凡,史守圆

(华南理工大学电力学院,广东广州 510640)

1 引言

非侵入式负荷监测(non-intrusive load monitoring,NILM)最早由Hart于20世纪80年代提出[1],作为高级量测体系(advanced metering infrastructure,AMI)[2]最重要的组成部分之一,该技术只在用户用电入口安装监测设备记录用电数据,利用监测算法分解负荷,得到内部负荷的用电状态和能耗信息.基于NILM,电网公司能以用户友好的方式了解负荷的状态和能耗,进而利用大数据等技术手段描绘负荷的用能模式和用户的用电行为,进而实现需求响应,优化电力资源配置,支撑智能电网的建设[3].

目前非侵入式负荷监测技术发展迅速,学者们已提出多种负荷识别算法.文献[4]设计了综合考虑稳态谐波电流和功率特征的正态分布度量函数,提出了一种基于改进鸡群算法的负荷监测方法.文献[5]构建了基于谐波的电流特征表达并结合功率作为设备投切状态辨识的目标函数,采用粒子群算法搜索实现NILM.文献[6]提出了一种关联循环神经网络模型的负荷辨识方法,对历史输入特征量进行记忆,提高对负荷特征辨识能力.文献[7]提出一种基于序列到序列和Attention机制的NILM模型,提升了对负荷信息的提取与利用能力.文献[8-12]均采用了改进或拓展的隐马尔可夫模型(hidden Markov models,HMM),使得算法运算速度和电器状态识别准确率得到较大提升.

以上NILM模型在特征提取或负荷辨识上有各自的优势,但是他们都缺乏对模型泛化能力的考虑.泛化能力是指一个模型对未知数据的适应能力,也可理解成学习到隐含在数据背后规律的能力.一个具备泛化能力的模型不单纯对数据集进行记忆,而可以挖掘同一问题背景下蕴含在数据中的共有规律,进而使模型在输入新鲜数据后也能给出合适的输出.泛化能力的缺失在基于HMM的NILM模型上尤为突出,HMM的观测概率和转移概率均通过历史数据进行计算,但过往的数据并不能保证负荷全部工作状态被测量,各状态的所有转移信息被确定,上述文献基于HMM的改进都是使其充分利用到已有的负荷信息,并未能考虑到因外部因素波动或自身电气特性改变引起的负荷特性变化和模型参数更新,导致其不具备泛化能力.本文认为,对HMM的泛化性能改进思路主要有以下3点:1)减小电压波动对负荷状态确定的影响;2)计及负荷的未知观测状态与新状态转移,即认为HMM的模型参数是不断更新的,来对负荷隐含状态进行预测计算;3)功率分解计算时考虑到功率的随机波动性.

为此,本文提出了一种基于二元参数隐马尔科夫模型(binary-parameter Hidden markov models,BPHMM)的非侵入式负荷监测模型.该模型先基于负荷有功功率和电流建立BPHMM,采用聚类算法(densitybased spatial clustering of applications with noise,DBSCAN)去除噪声数据并对负荷状态进行聚类;负荷隐含状态序列进行编码后,改进维特比算法提高其对HMM模型参数更新的适应能力,进而实现负荷状态序列最优预测;得到负荷状态预测序列后,计及功率随机波动性,基于极大似然估计原理建立功率分解优化模型,并根据负荷各工作状态聚类簇的均值与方差进行功率分解计算,最后通过算例验证了所述方法的准确性.

2 BPHMM的建立

本节首先提出并建立本文所提的二元参数隐马尔科夫模型,然后对其中各个环节特别是泛化性能的改进进行详细的说明.

2.1 HMM简介

隐马尔科夫模型是关于时序的概率模型[13].隐马尔可夫模型中,存在一条值不可测量的时间序列和一条值由前述时间序列决定的可测量时间序列.值不可测量的时间序列称为隐含状态序列,值可测量的时间序列称为观测序列.其模型结构如图1所示.

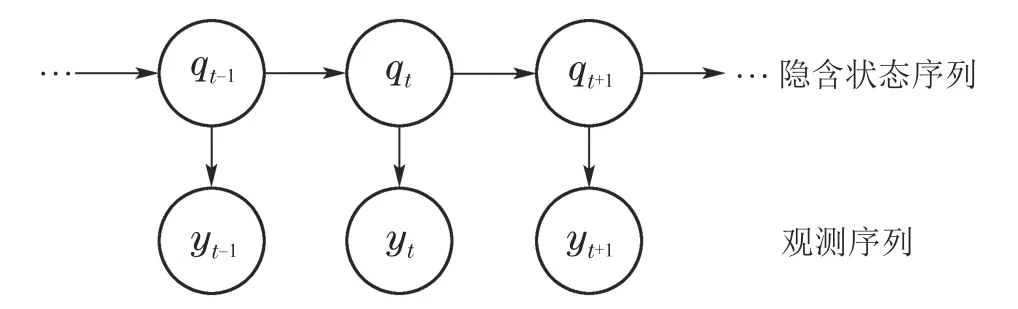
图1 隐马尔科夫模型结构图Fig.1 Structure chart of hidden Markov model

一个HMM模型可由以下参数描述.

1) 隐含状态集合S:

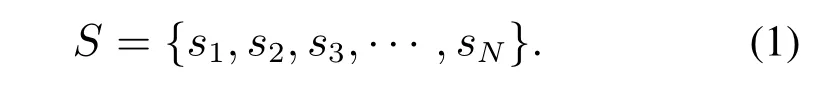
2) 观测状态集合V:

3) 状态转移矩阵AAA:

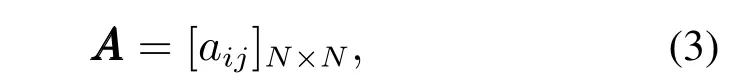
其中aij=P(qt+1=si |qt=si).

4) 输出矩阵BBB:

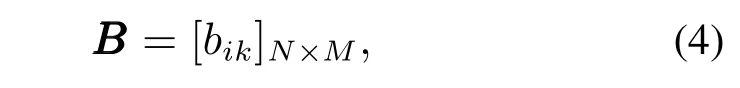
其中bik=P(yt=vk |qt=si).

5) 初始概率矩阵π:

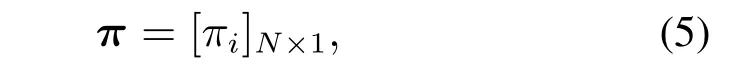
其中πi=P(q1=si).

由上述各式可知:状态转移概率矩阵AAA与初始状态概率向量π确定了隐含状态序列,观测概率矩阵BBB确定了如何由隐含状态推导出观测状态,结合状态转移概率矩阵AAA就能产生测量序列,隐含状态个数N和观测状态个数M实际上由以上3个矩阵定义,因此隐马尔可夫模型可以用λ={AAA,BBB,π}表示.

HMM被用于研究以下3类问题:

1) 概率计算问题.给定模型λ={AAA,BBB,π}和观测序列O={O1,O2,···,OT},计算P=(O |λ).

2) 学习问题.给定观测序列

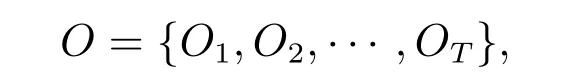
估计模型λ={AAA,BBB,π}参数,即寻找P=(O |λ)最大值,也就是用极大似然估计的方法去估计参数.

3) 解码问题.已知模型λ={AAA,BBB,π}和观测序列O={O1,O2,···,OT},求对给定观测序列条件概率P=(I |O)最大的状态序列I={I1,I2,···,IT},即根据给定观测序列预测对应的隐含状态序列.

2.2 问题建模与参数计算

在NILM研究中,HMM两条时间序列的物理意义是:隐含状态序列对应电器序列中各用电器的运行状态(为方便下称总状态).观测序列对应可测量的电气量.因此NILM问题就转化为给定HMM模型参数与测量序列,求该测量序列对应的可能性最大的隐含状态序列,即解码问题.

更进一步,本文把NILM问题建立成二元参数隐马尔科夫模型BPHMM并计算其参数:

1) 隐含状态集合S:在NILM问题中,S表示为总状态的集合.该集合是各用电器运行状态的全排列,集合元素个数由各用电器状态聚类数目决定,其值用第3.1.3节介绍的状态编码方式计算.

2) 观测状态集合V:在NILM问题中,V表示用户用电入口测量到的用电信息数据的集合.特别的是,一般HMM模型集合V的元素是总有功功率,但在本文提出的BPHMM中,集合V中的元素是由总有功功率和总稳态电流构成的向量vi=.

3) 状态转移矩阵AAA:aij指的是从时刻t的各用电器的总状态qt=si转移到t+1时刻的总状态qt+1=sj的概率.计算方法:

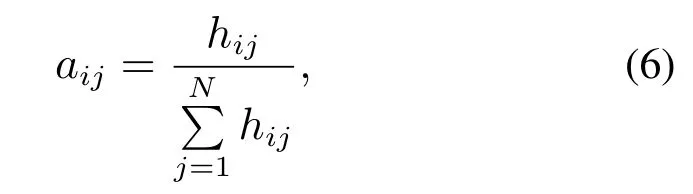
其中:hij是总状态qt=si转移到t+1时刻的总状态qt+1=sj的频数,N是隐含状态总数.

4) 输出矩阵BBB:表示t时刻各用电器处于总状态qt=si而测量值为yt=vk的概率.计算方法:

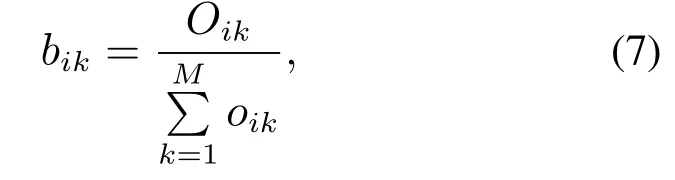
其中:Oik是t时刻总状态qt=si而测量值为yt=vk的频数,M为测量值总数.

5) 初始概率矩阵π:πi表示初始时刻,各用电器总状态处于si的概率.计算方法:

其中:d是训练集数据总量,di表示训练集中隐含状态si出现的频数.

需要指出的是,针对多用电器的HMM建模,可以采用因子隐马尔科夫模型(factorial hidden Markov model,FHMM),FHMM包含了多条隐含状态链,能分别对应每一个要研究的电器.但相关研究表明,FHMM预测的状态识别精确度偏低[14].因此本文在经典HMM模型基础上进行改进,配合第3.1.3节提出的状态编码方式,解决了HMM隐含状态难以用向量表示的问题,同时没有使各用电器的状态转移矩阵解耦,相比FHMM理论上保留了不同电器状态转移之间的信息.

3 基于BPHMM的泛化性能改进

3.1 基于DBSCAN的负荷状态聚类与编码

负荷特征的选择决定了负荷状态的物理描述,而聚类是负荷状态的确定方法,选择负荷特征和聚类方法是泛化性能改进的第1步.

3.1.1 负荷特征选取

目前,NILM的研究所选取的负荷特征大致可分为暂态与稳态两种.由于暂态特征一般为合成数据,不是由计量装置真实采集的,实用性不强,故本文选取稳态电气量作为负荷特征.

稳态电气量主要包括电压、电流、有功功率、无功功率和视在功率.有功功率是功率分解计算的指标,NILM需要在状态预测完成后给出负荷有功功率的分解值,所以有功功率是大多数NILM研究所采用的特征.然而,稳态功率细微波动较大,稳态电流受电压波动影响更小,计算得到的负荷识別精确度更高[15],这有助于降低因电压波动对负荷运行状态误分类的可能性,进而提高模型的泛化性能.因此本文选取负荷的有功功率和稳态电流作为负荷特征.

3.1.2 负荷状态聚类

各类负荷因自身电气特性或工作条件不同,其运行时的运行状态具有差异,从负荷监测的角度,可依据运行状态将电器分为开关状态型电器、有限多状态型电器、连续变状态型电器3类[1].前两种类型电器运行状态个数可数,理论上能获得其全部运行状态,但连续变状态型电器工作状态是连续变动的,需要采用聚类算法对运行状态进行聚类,使其离散化转变成有限多状态型电器继续研究.

考虑到历史数据存在噪声点,将干扰模型学习数据背后的隐含规律,对模型泛化性能造成不利影响,本文采用DBSCAN聚类算法对电器负荷特征进行提取和聚类.DBSCAN算法由Martin Ester等人在1996年提出,是一种经典具有代表性的基于密度的聚类方法[16].DBSCAN的核心思想是:从某个选定的核心点出发,不断向密度可达的区域扩张,从而得到一个包含核心点和边界点的最大区域,区域中任意两点密度相连.因此,与k-means等常用聚类算法对比,该算法聚类数目不需要事先确定,且可以在含有噪声数据的数据集中识别任意数量和形状的聚类[17].DBSCAN算法聚类簇示意图及具体执行流程图如图2-3所示.

由图2可知,在DBSCAN算法中,聚类簇参数由簇半径ε以及最少样本数minpts决定.本文通过手肘法寻找出最优的ε和minpts.手肘法是指选用不同的参数组,并将不同参数组对应的评估指标结果画成折线,此时将存在一个拐点,将曲线分为急速变化和趋于平稳两部分,就像人的肘部一样,手肘法认为拐点就是参数的最佳值.本文选择最常用的轮廓系数作为手肘法的评估指标.

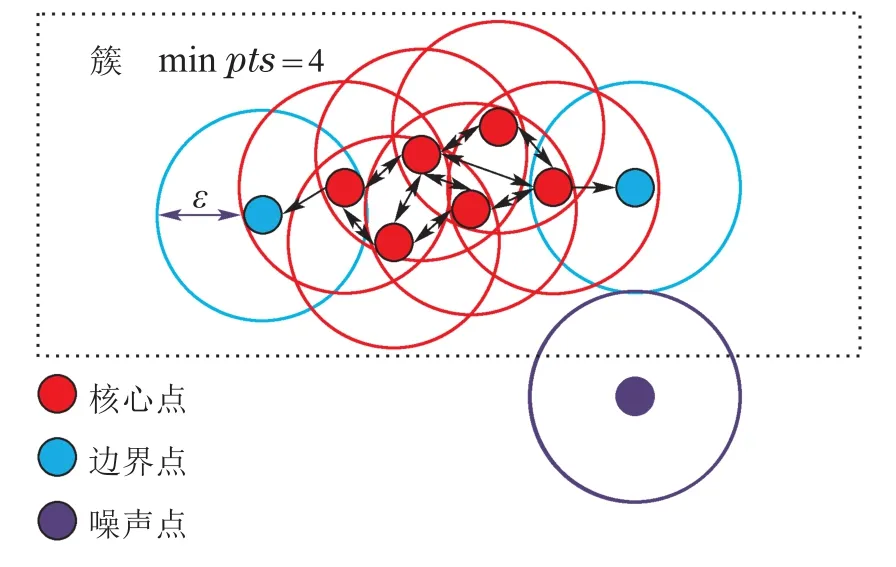
图2 DBSCAN算法各参数解释图Fig.2 Explanation chart of DBSCAN algorithm parameters

3.1.3 状态编码

在多数研究中,一般采用向量来表示某时刻负荷序列的总状态,如假设3个负荷的状态个数分别为2,3,8,该时刻所处状态分别为0,2,5,那么就能用向量s=[0,2,5]来表示该总状态.然而在HMM应用中,隐含状态并不能用向量表示.为此,本文提出了一种基于二进制的状态编码方式,将各负荷的隐含状态向量编码为一个二进制状态值,结合上面实例,具体步骤如下:

1) 分配位数.根据电器的状态数确定编码所需要的二进制位数.上面3个电器状态个数分别为2,3,8,则分配给各个电器的二进制位数分别为1,2,3.

2) 确定取值.根据当前时刻电器的十进制状态值计算二进制状态值.当前3个电器十进制状态值分别为0,2,5,则二进制状态值分别为0,10,101.

3) 拼接表示.将所得到的二进制状态值根据电器排序从高到低拼接,得到最终的结果.当前时刻状态向量经拼接表示后的状态值为010101.

表1为该编码方式的其他示例.

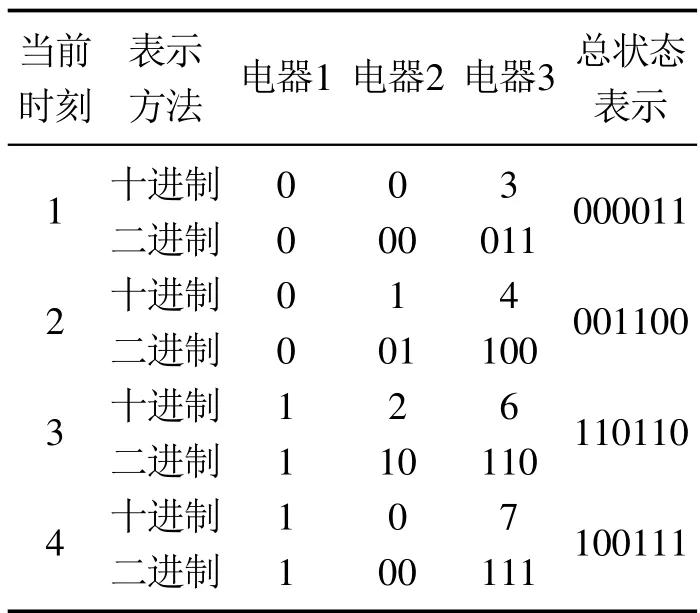
表1 部分电器状态编码表示Table 1 State code of some electrical appliances

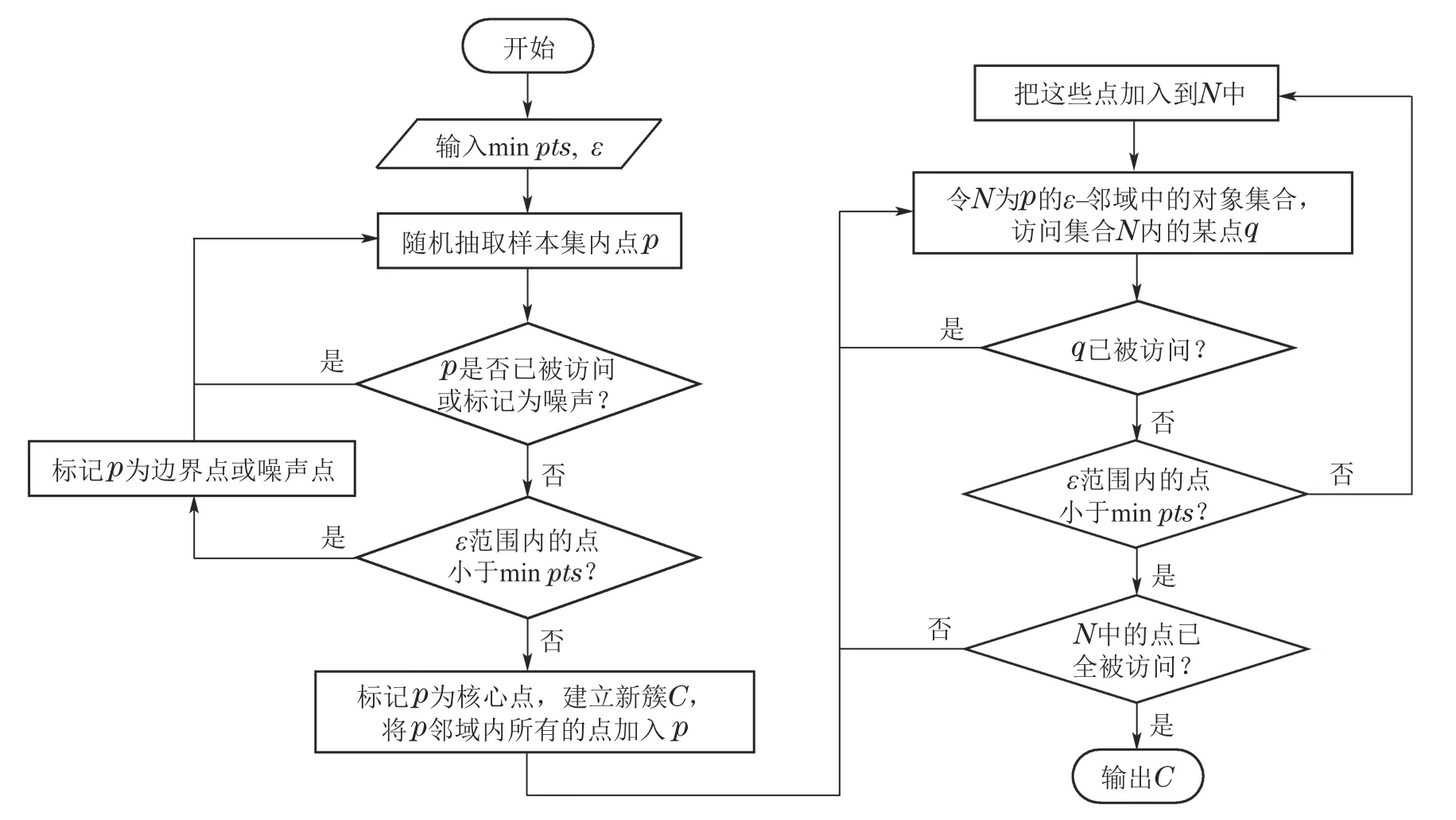
图3 DBSCAN算法流程图Fig.3 Flow chart of DBSCAN algorithm

3.2 计及负荷未知观测状态与新状态转移的隐含状态预测

负荷序列总状态编码完成后,即可通过维特比算法进行最优隐含序列的预测.维特比算法(Viterbi algorithm)由美籍意大利科学家安德鲁·维特比于1967年提出,用于求解最短路径问题,被广泛用于解码和自然语言处理等领域[18].

维特比算法的基本思想是从t=1时刻开始,递归地计算转移到t时刻各个状态i的最大概率:

维特比算法是动态规划思想在最短路径问题上的一种具体实现,所以只需要证明维特比算法符合动态规划的定义即可,其最优性将自然由动态规划的性质给出.作为一种动态规划算法,需要满足最优化原理和无后效性两个条件.最优性原理是指不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略.简而言之,一个最优化策略的子策略总是最优的.无后效性是指对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态.换句话说,每个状态都是过去历史的一个完整总结.

维特比算法的最优性原理能由反证法得出:若最短路径P经过某点x,那么这条路径上从起始点s到该点的这段子路径Q,一定是这两点之间的最短路径.否则,用s到x的最短路径R替代Q,便构成一条比P更短的路径,这显然是矛盾的.由式(9)可知,维特比算法所求的最短路径其实是求一个从t-1时刻出发的,转移到t时刻状态i概率最大的状态,所谓的路径最短实质是概率最大,而且概率计算就是基于马尔科夫性得到的,即当前时刻的状态仅与前一时刻的状态和动作有关,与其他时刻的状态和动作条件独立,满足无后效性,维特比是动态规划算法得证.由动态规划性质可得,若能将原问题分解成若干个子问题,则只要求当前子问题的最优解,最后就能得到原问题的最优解.

在NILM问题上应用维特比算法需要考虑泛化能力.若以统计学的观点去分析,泛化能力可认为是在信息有限的情况下,去找出数据所属的分布,以及该分布的模型参数的能力.在实际的NILM应用中,历史数据并不能反应负荷所有工作状态及状态之间的转移关系,且新测量到的电气数据也不全与已测量到的数据吻合,换而言之,状态的观测概率和转移概率并不是完全已知且准确的.由于经典维特比算法实现的前提是HMM的模型参数已知,不具备泛化能力,但历史数据又只包含了真实数据分布的部分信息,因此经典维特比算法将难以准确求解NILM场景下最优隐含序列的预测问题.

针对上述困难,本文提出了改进维特比算法,其主要思路是:若模型只掌握关于未知分布的部分信息,且符合已知信息的概率分布可能不止一个,那么模型就应该基于极大似然估计,选取符合这些信息但概率最大的概率分布.其具体改进如下:1)考虑到电器将出现新的观测状态,且该观测状态可能对应未知运行状态的问题,本文将输入的电气数据用k-means算法聚类到已知测量状态中;2)考虑到电器可能存在新的状态转移,基于极大似然估计改变了δ和ψ的计算方法;3)考虑到状态转移矩阵和测量矩阵的稀疏性,参考文献[19]提出的稀疏维特比算法,只处理状态转移概率及测量概率均不为0的计算.

对于给定观测序列Y={y0,y1,···,yT}和隐含状态序列Q={q0,q1,···,qT},本文提出的改进维特比算法计算具体步骤如下:

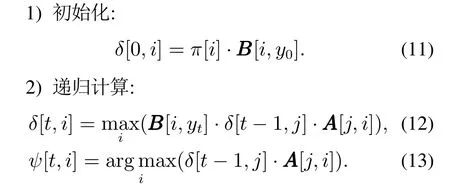
特别地,不妨设t时刻的测量状态yt=k,该观测状态发生时,根据极大似然估计原理,出现概率最大的隐含状态应该是满足bik=max(B[:,k])的状态i.当计算δ[t,i]和ψ[t,i]时,将以上两式的计算改为

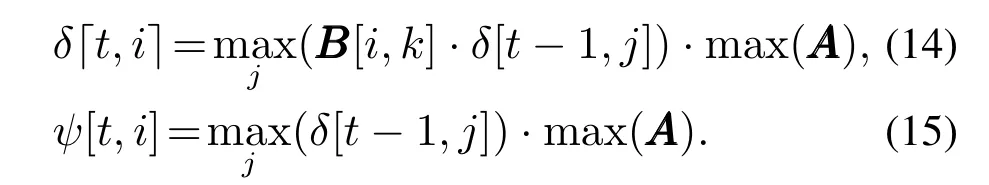
该改进方法将在考虑到新的状态转移上求得最优解,数学证明如下.

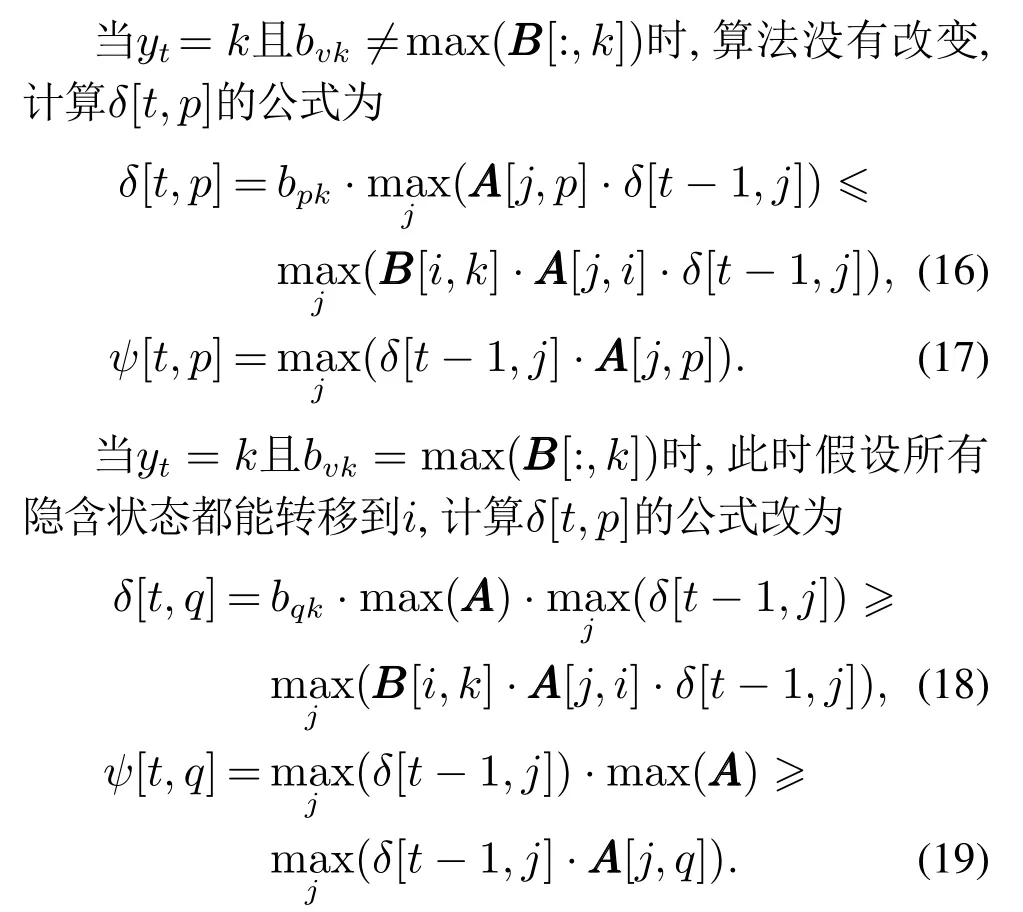
维特比是动态规划算法,他只关注每一步的最优解,研究未知但确定是非最优的解是不必要的,所以本文只关注满足bvk=max(BBB[:,k])的状态i所出现的新状态转移.转移概率取max(AAA)的原因是为了避免经过该点的路径被算法放弃,若aji不取max(AAA)而取其他合法值,虽然仍然能正确得到ψ[t,i]的结果,但是会使δ[t,i]的值变小,进而降低未来时刻最优路径途径该点的概率.

3) 终止状态计算:

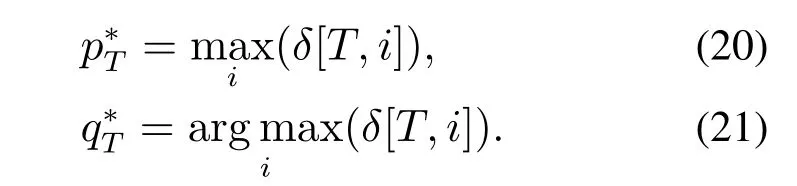
4) 最优序列回溯:

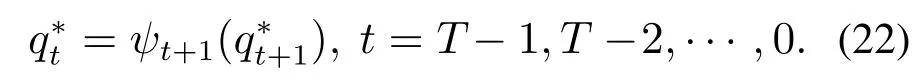
此时得到的序列即是预测最优隐含状态序列

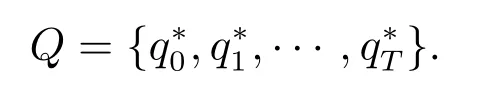
3.3 考虑随机波动性的功率分解

得到预测状态序列后,便可根据其结果进行负荷功率分解.负荷在某一稳定运行状态下的功率存在波动性,而这种波动性可以认为是某一概率分布下的随机测量[20-21].基于上述结论,本文改进模型泛化性能的思路是让模型意识到功率数据波动背后的统计分布.据此,本文作出历史功率数据的频率分布直方图,绘制密度分布曲线,观察得出负荷稳定运行时功率数据的统计分布与正态分布最为相似,并注意到分解后负荷功率之和等于总功率的这一约束条件,提出一种基于极大似然估计原理的功率分解优化模型,并用于负荷功率的分解计算.

本文的功率分解计算步骤是:1)根据各负荷样本的聚类簇的平均值与方差,建立各负荷各状态的正态分布概率密度函数;2)基于极大似然估计建立目标函数,即求联合概率的最大值,并计及同一时刻各负荷功率监测值之和应等于总功率这一约束条件,构建功率分解计算模型如下:

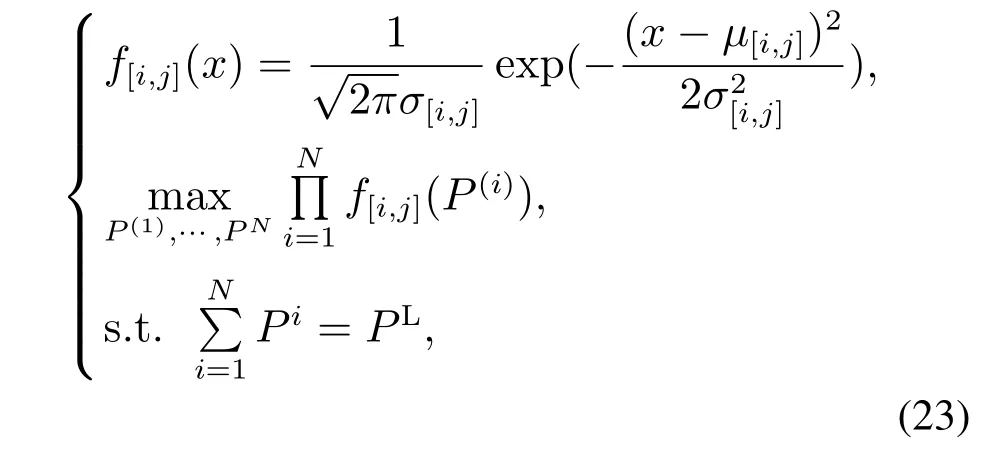
式中:σ[i,j]和µ[i,j]分别指第i个电器的第j个聚类簇的标准差和均值,N为电器个数,P(i)指每个电器的分解有功功率,PL指总负荷的有功功率.f[i,j](P(i))指电器i处于j运行状态时消耗功率P(i)的概率.上述问题将目标函数两边取ln()后就是一个常见的凸二次规划问题.

本文提出的非侵入式负荷监测方法完整流程如图4所示.

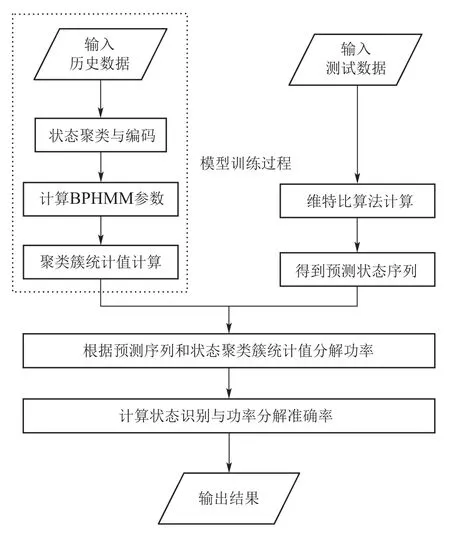
图4 基于BPHMM的非侵入式负荷监测流程图Fig.4 Flow chart of non-intrusive load monitoring based on BPHMM

4 算例分析

4.1 实验方法

由于本文的研究工作最终将面向需求响应,实现用户侧负荷辨识与控制功能,因此作为评估验证的数据集应满足需求响应下的应用特点即分钟级采样频率,长采样时间、拥有电流和功率采样数据等.综上所述,本文选取加拿大学者Stephen Makonin等建立的公共数据集AMPds2,以验证本文所述方法[20-21].AMPds2采集的为一户家庭中用电设备的真实电气数据,能展现日常使用时功率和电压可能遇到的波动.该数据集记录了包括稳态电流、有功功率等11种电气特征,采样频率为Hz,纪录时长2年,适合作为算例分析数据集.

从数据集中选取壁炉(WOE)、衣物烘干机(CDE)、洗碗机(DWE)、电视机(TVE)、洗衣机(CWE)、热泵(HPE)6种电器共10天14400个采样点的有功功率与稳态电流数据并按时间均分为10组,记为test 1～test 10,进行10折交叉验证,每一次实验依次选取其中9组数据作为训练数据,1组作为测试数据,最后计算平均值.

运行本文所述算例程序的计算机配置为16 GB RAM with Inter(R) Core(TM) i5-8300H @2.30 GHz,程序使用Python语言编写.

4.2 实验结果

4.2.1 基准负荷监测结果

本文采用基本准确率ACCstate评价负荷状态识别准确率,用均方根误差(root mean square error,RMSE)评价负荷功率监测准确性:

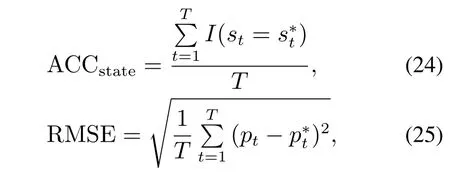
式中:T为采样时段长度,st和pt为该电器在t时刻的实际状态和实际功率值,为预测状态和分解功率值,I()为指示函数.

测试集中某一天热泵和电视机的分解结果分别见图5-6.图5(上)和6(上)为实际功率,图5(下)和6(下)为分解结果.全部电器的功率分解结果见附录A.

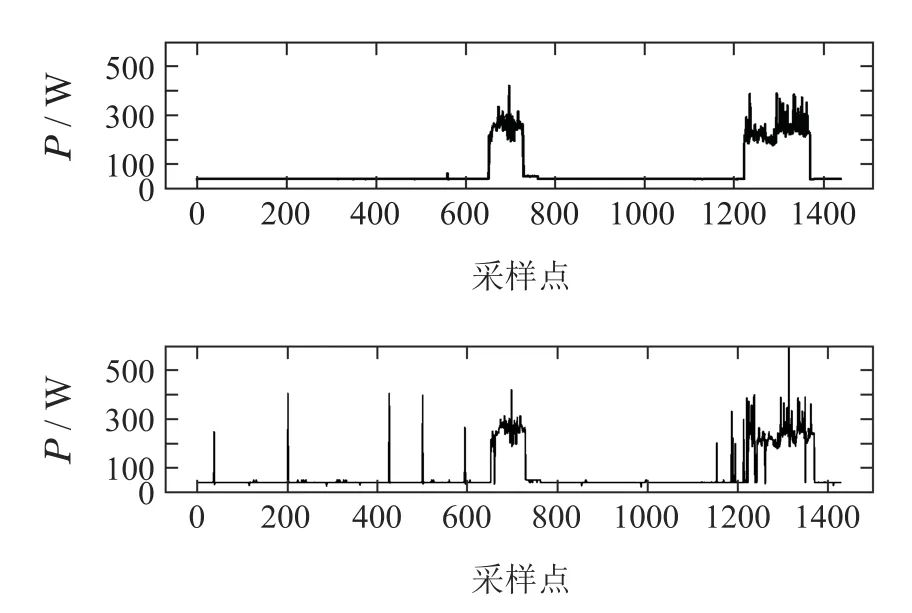
图5 热泵的功率分解结果Fig.5 Results of power disaggregation(HPE)

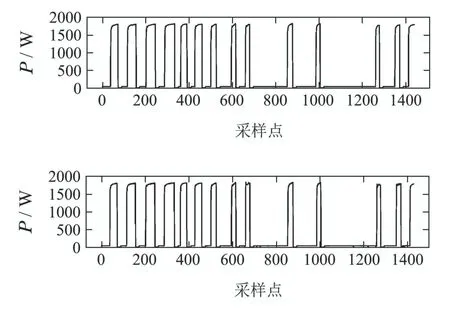
图6 电视机的功率分解结果Fig.6 Results of power disaggregation(TVE)

本文选取文献[23]所提出的基于遗传算法(genetic algorithm,GA)的分解方法、文献[24]基于深度序列翻译模型(recurrent neural networks,RNN)的分解方法以及经典HMM[13]作为对比,采用相同数据分别进行10折交叉验证计算平均值,4种方法的负荷状态识别平均准确率,功率分解均方根误差分别如表2和图7所示.

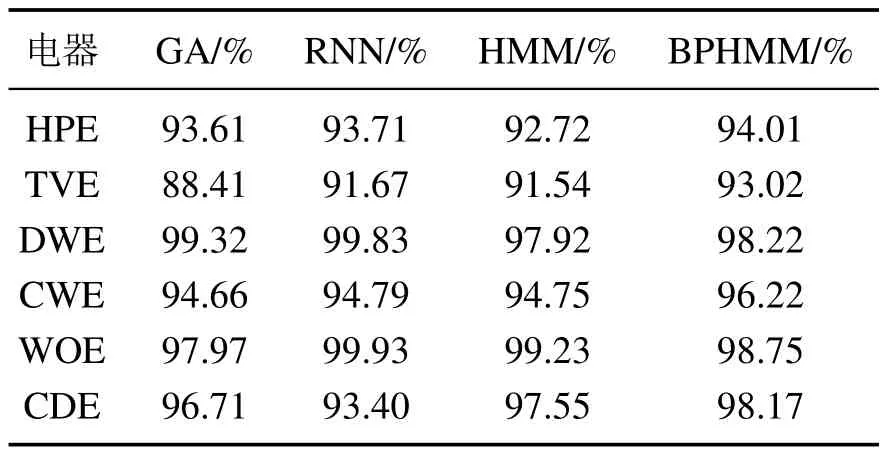
表2 状态识别平均准确率对比Table 2 Comparison of precision of state recognition

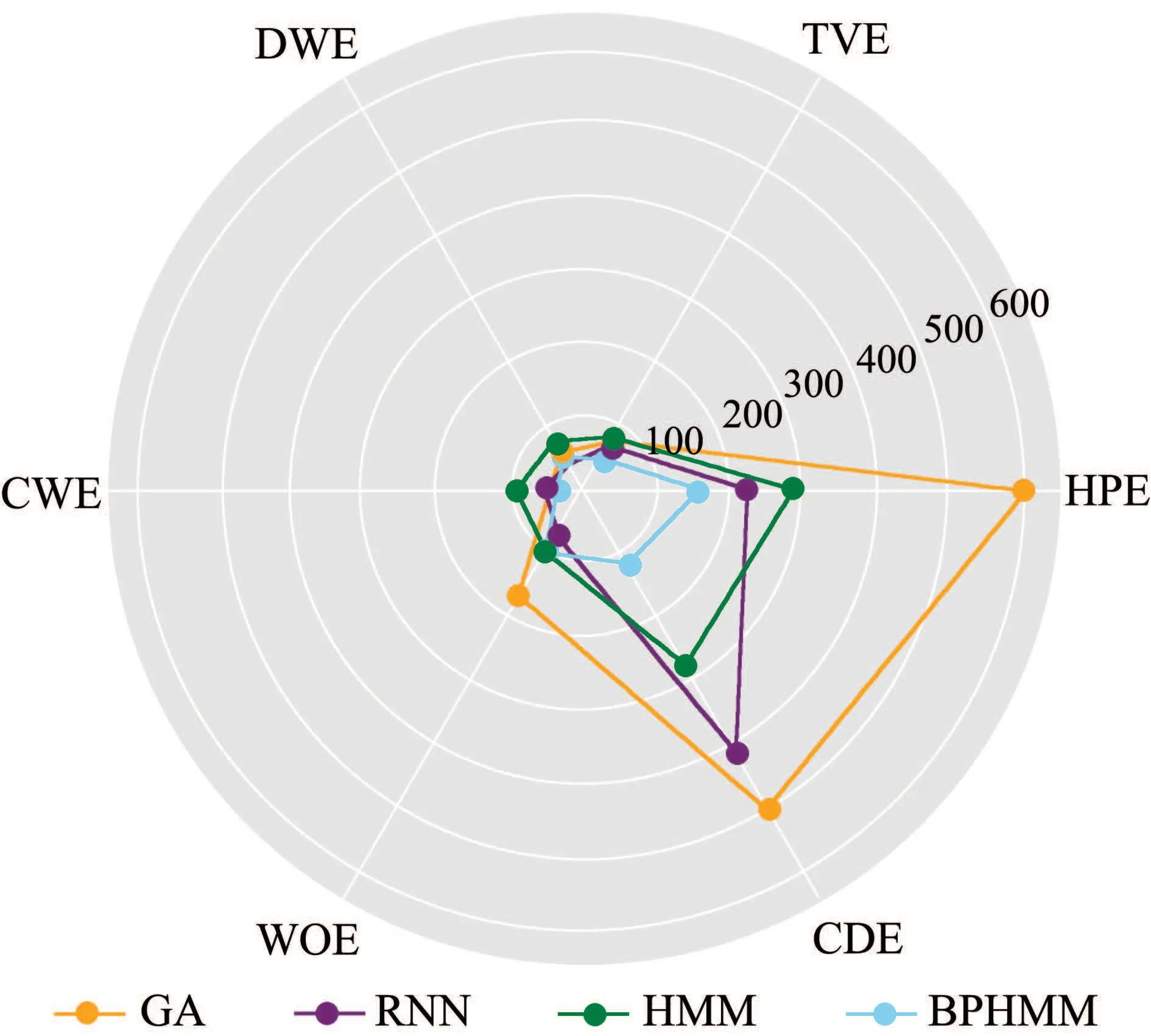
图7 功率分解均方根误差对比Fig.7 Comparison of RMSE of power disaggregation

4.2.2 泛化性能实验结果

一般地,机器学习泛化性能指标一般是将其他同类数据集作为测试集,测试模型是否能给出恰当的输出.但在NILM问题中,要找到另外一个采样频率、采样电器、采样电气特征均相同的公共数据集较为困难,因此本文仍采用AMPds2数据集,在模型参数不变的情况下进行泛化性能实验.泛化性能实验结果已上传至Google Driver,获取路径见附录B.

1) 缺失负荷.

取除训练集与测试集数据以外的包含衣物烘干机(CDE)、电视机(TVE)、洗衣机(CWE)、热泵(HPE)和壁炉(WOE)5种电器的有功功率与稳态电流数据共10天作为新的测试集,以考察模型在面对新鲜数据与电器缺失时的适应能力.上述4种方法的负荷状态识别平均准确率,功率分解均方根误差分别如表3和图8所示.

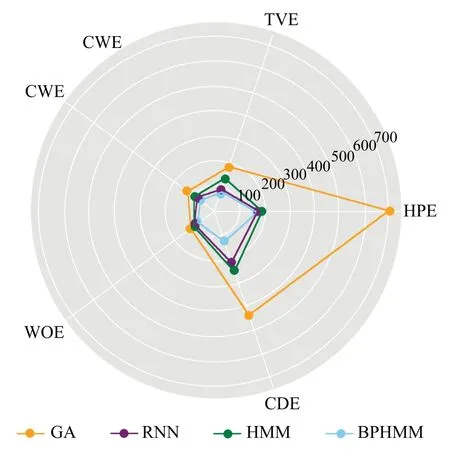
图8 功率分解均方根误差对比Fig.8 Comparison of RMSE of power disaggregation

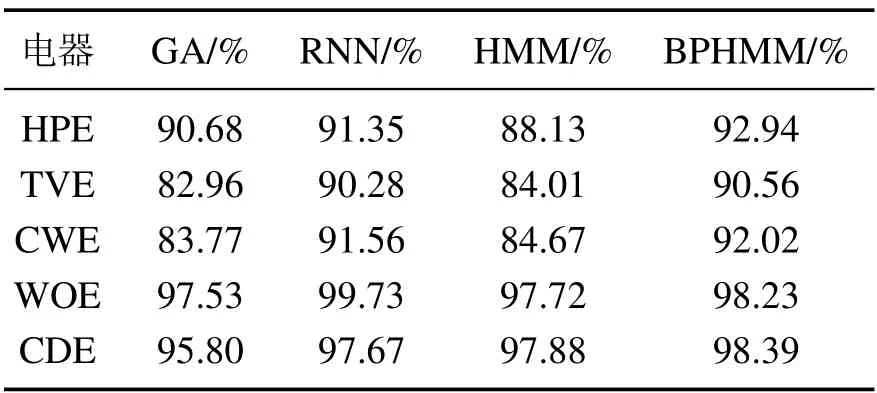
表3 状态识别平均准确率对比Table 3 Comparison of average accuracy of state recognition

2) 使用其他负荷替换已知负荷.

在模型参数不变的情况下,将洗碗机(DWE)替换为冰箱(FGE),其余5种负荷不变,取除训练集与测试集数据以外10天数据作为新的测试集,以考察模型在面对新鲜数据与未知负荷时的适应能力.上述4 种方法的负荷状态识别平均准确率,功率分解均方根误差分别如表4和图9所示.值得指出的是,冰箱是未知负荷,所以状态集合未知,状态识别准确率无意义,故本文仅给出未被替换的5种已知负荷的状态识别准确率,因冰箱功率能被观测,故功率分解误差指标仍然有效.

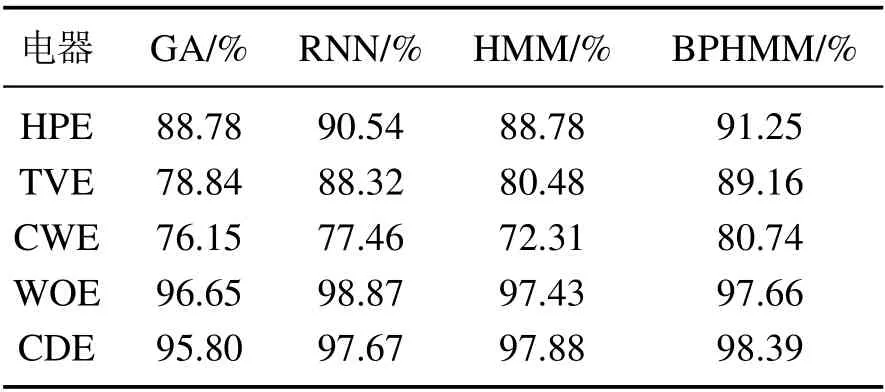
表4 状态识别平均准确率对比Table 4 Comparison of average accuracy of state recognition

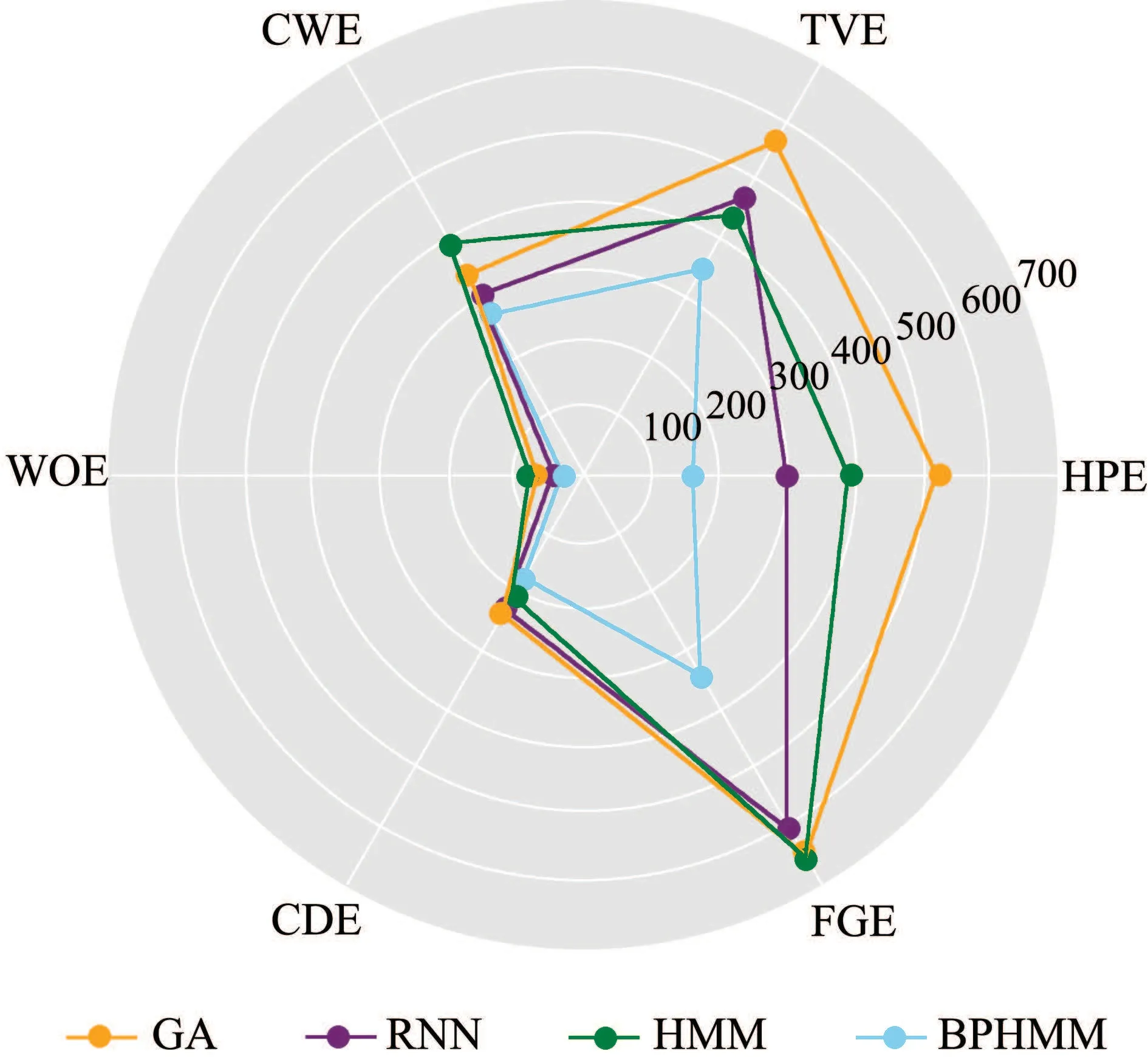
图9 功率分解均方根误差对比Fig.9 Comparison of RMSE of power disaggregation

4.2.3 运算速度对比与结果分析

从表5可知,由于BPHMM使用了稀疏矩阵运算方法,在运算速度上对比经典HMM存在一定的优越性.同时,由上述结果可以看出,本文所述方法对组合电气特征的利用能使模型提取出更能体现负荷电器特性的运行状态,且一定程度削弱了因外部环境带来的电压波动,从而对NILM问题求解性能指标改善有帮助.本文提出的基于极大似然估计的功率分解优化模型,一定程度上考虑并学习到了功率数据波动性的概率分布,保证了各个电器的监测功率之和等于总负荷功率,使功率分解准确率更高.对比较为前沿的深度学习方法,本文所述方法在多工作状态电器如电视机和洗衣机的状态识别准确率上优于基于深度学习的解决方法.在泛化性能实验中,本文所述模型将HMM与极大似然估计结合,让传统隐马尔可夫模型对新鲜数据输入导致的已知概率分布出现改变这一现象进行适应,初步改善过往的数据并不能保证负荷全部工作状态被测量,各状态的所有转移信息被确定的问题,这也表明计及并提高泛化性能的解决思路对提高NILM问题求解准确性有效.

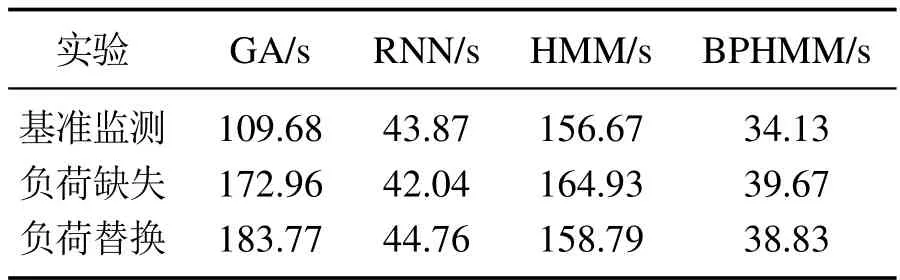
表5 各模型运算速度对比Table 5 Comparison of operation speed of each model

5 结论

本文提出了一种基于HMM的非侵入式负荷监测泛化性能改进方法.该方法提出并构建了二元参数隐马尔科夫模型BPHMM,采用DBSCAN聚类算法对负荷特征进行聚类,提出一种基于二进制的编码方案对负荷状态组合进行编码,改进了维特比算法使其具备对模型参数更新的适应能力进而实现负荷状态的最优预测,最后建立计及功率随机波动性的优化模型,根据电器聚类簇的均值和方差实现负荷的功率分解.算例结果表明,相比基于启发式算法,深度学习方法以及经典HMM的识别方案,本文所提方法取得了更高的负荷状态识别准确率与更低的功率分解误差.本文针对NILM模型泛化性能提高所提出的各项措施如对数据进行降噪处理、改进传统方法使其提高对未知数据的适应能力以及使模型学习到数据波动背后的统计特性等思路,相信对NILM的实用化有参考价值.本文工作对泛化性能改进的研究还比较初步,也没有考虑到负荷运行的非电气特征.下一步研究将关注如何利用非电气特征,如负荷工作时长、用户行为习惯等;研究新增未知电器的处理,提出更具有实用性的非侵入式负荷监测方法.

附录

A 基准测试分解结果

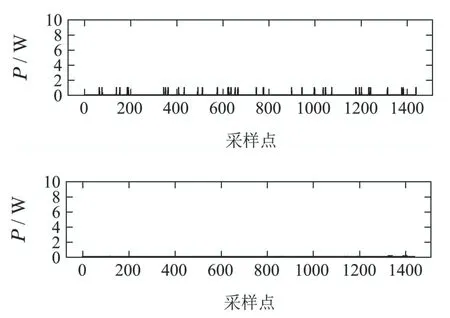
图A1 壁炉的功率分解结果Fig.A1 Results of power disaggregation(WOE)

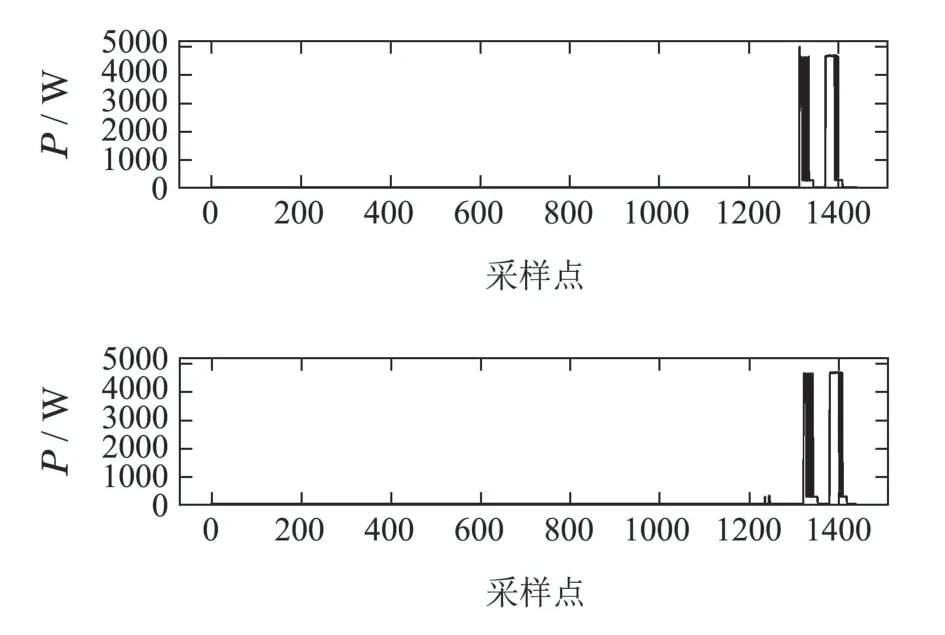
图A2 衣物烘干机的功率分解结果Fig.A2 Results of power disaggregation(CDE)

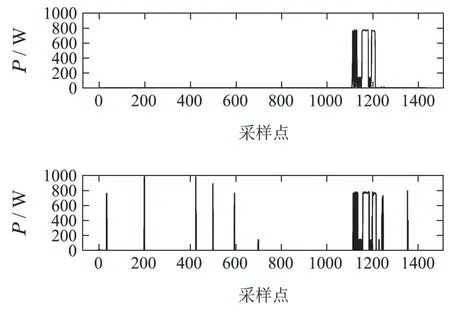
图A3 洗碗机的功率分解结果Fig.A3 Results of power disaggregation(DWE)

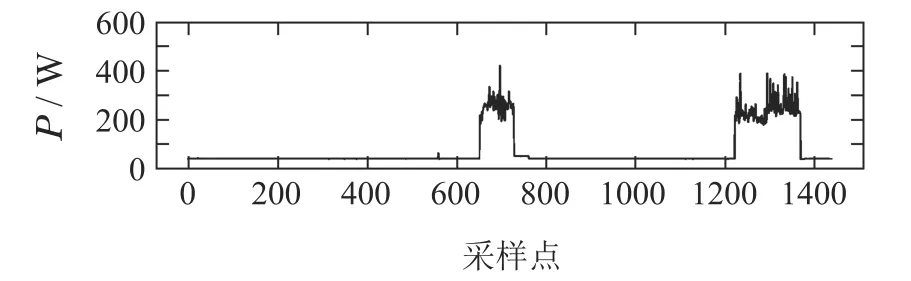
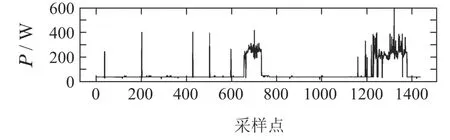
图A4 电视的功率分解结果Fig.A4 Results of power disaggregation(TVE)

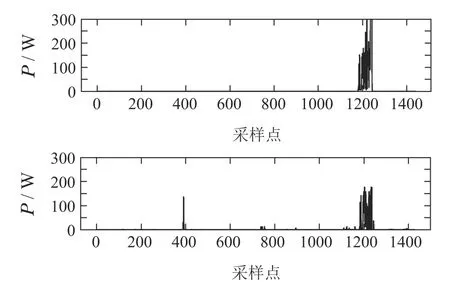
图A5 洗衣机的功率分解结果Fig.A5 Results of power disaggregation(CWE)

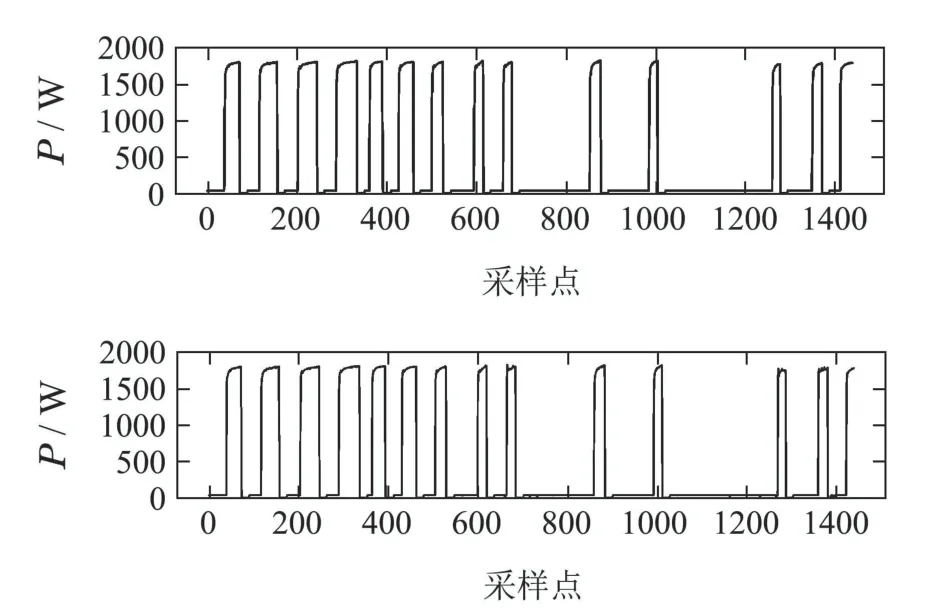
图A6 热泵的功率分解结果Fig.A6 Results of power disaggregation(HPE)

B 泛化性能测试分解结果获取路径

https://drive.google.com/drive/folders/1jGwK6bzzHlQlc-VT8LYsdIuVpGiP84DU?usp=sharing