不同竞争环境下损失厌恶与网络销售效率对双渠道供应链的影响

邱国斌 ,徐 兵

(1.南昌航空大学经济管理学院,江西南昌 330063;2.南昌大学管理学院,江西南昌 330031)

1 引言

进入21世纪,电子商务与制造业的发展日新月异,国内外众多杰出的电商平台,如淘宝、亚马逊等,已经成为引领大众网络消费的主要渠道.随着电商平台获得越来越多的市场份额,很多优秀的制造商们也不甘示弱,如海尔、联想等,这些企业在传统批发零售渠道的基础上,纷纷将眼光投向网络销售渠道.显而易见,制造商的涌入对电商平台造成了不小的冲击,但与电商平台相比较,制造商在网络销售效率方面仍然存在短板.与此同时,电商平台与制造商的竞争环境也变得更加复杂,市场的瞬息万变导致企业的主导地位交替更迭.当然,这种双渠道供应链模式为消费者提供了更多的选择机会,消费者对产品的性价比也更加期待.然而,现实并不总是令人满意,消费者在网购过程中经常会遭受各类损失,很多消费者对于损失往往又存在厌恶心理.例如,若消费者在电商平台购买了伪劣产品,往往会在网上发表差评,要求商家退货索赔,甚至向工商管理部门进行投诉等.面对错综复杂的竞争环境、制造商的网络销售效率以及消费者的损失厌恶心理,这些综合因素会对电商平台和制造商的决策产生什么影响?供应链的整体绩效将会发生怎样的变化? 所以不同竞争环境下网络销售效率与损失厌恶对双渠道供应链的影响研究具有重要的研究价值.

网络销售效率是双渠道供应链成员企业之间博弈的重要影响因子,学者们就此问题进行了相关研究.如李陈华[1]研究了网络销售效率对双渠道供应链企业定价决策的影响,发现当网络销售效率较高时,销售价格将会下降,若市场很大,则零售企业较高的直销销售效率将促使制造商扩大网络销售渠道.刘汉进等[2]在网络销售效率存在高低的情况下分析了网络销售对于双渠道销售数量产生的影响,发现当网络销售效率较低时,传统渠道的销售数量将会增加,反之,将会减少.张廷龙等[3]分析了网络销售效率对于企业定价决策优化,以及双渠道供应链协调产生的影响.Yan等[4]针对某电商平台分别以分销模式和平台模式销售同一种产品,研究两种模式的效率差异对于产品定价的影响.研究显示,若平台费用增大,则两种模式下的产品价格均将增大.Chen等[5]在制造商组建的双渠道供应链环境下,分析了其直销服务水平与零售商的零售服务水平的决策优化问题.研究表明,网络销售效率与消费者的忠诚度均对两种服务水平产生重要影响.

损失厌恶是指人们在面对相等数量的收益与损失时,对遭受的损失表现出的厌恶程度强于对获得的收益表现出的满意程度[6].决策者的损失厌恶心理广泛应用在储多行业领域.如He等[7]分析了损失厌恶心理对投资领域产生的影响.Wang等[8]研究了基于参照点的损失厌恶报童模型,并对其最优订货与传统报童进行了比较分析.Liu等[9]以需求更新为背景,通过4种模型对比分析了损失厌恶对企业订货决策的影响.Wu等[10]基于Stackelberg博弈模型,构建了零售商和供应商分担损失和贸易信贷的供应链模型.研究表明:供应商通过交易信用和损失分担能够提升损失规避零售商的效用.Qiu等[11]探究了具有参照点效应的损失厌恶零售商的联合定价与库存决策优化问题,得到了最优定价和最优库存决策模型.申成霖等[12]探究了消费者的策略行为,以及零售商的损失厌恶心理对供应链企业决策产生的影响.余建军等[13]在可靠供应、不可靠供应和双源供应情形下,研究了损失厌恶零售商的订货问题,发现在双源供应情形下的企业效用最大.单汨源等[14]对损失厌恶供应链的协调问题进行了研究,得到成本分担契约能够实现帕累托改进.李锋等[15]考虑到不确定性市场需求,研究了损失厌恶企业决策者的决策问题.冯中伟等[16]研究了损失厌恶与破裂风险的Rubinstein谈判博弈问题,证明子博弈完美均衡的存在性和唯一性.顾波军等[17]运用Stackelberg博弈模型,研究零售商回扣与订单联合决策以及供应商渠道销量回扣决策问题,得到分散决策供应链回扣联合促销机制.马超等[18]运用Nash均衡博弈模型,研究损失厌恶供应商与风险中性制造商之间存在的产能矛盾问题,发现风险分散契约能够协调供应链.

近些年来,有学者发现消费者也广泛存在损失厌恶心理,而有关研究相对较少.如柳键等[19]研究了消费者的损失厌恶心理对企业决策优化和供应链补偿契约产生的影响.胡礼梅等[20]基于在线数值评分数据,构建了产品推荐模型,帮助损失厌恶消费者如何定位所需商品.

综上所述,虽然网络销售效率与损失厌恶心理都会对企业决策与绩效产生重要影响.但是,已有文献只是分别研究了网络销售效率、损失厌恶对供应链的影响,并没有将网络销售效率与损失厌恶结合起来进行综合分析.鉴于此,本文在考虑制造商存在网络销售效率问题,以及消费者存在损失厌恶心理的基础上,在不同的竞争环境下,研究了双渠道供应链企业的网络定价决策优化问题,得到的结论能够为电商平台与制造商企业提供决策参考.

本文与已有研究的区别在于:一是将网络销售效率和损失厌恶结合起来,深入研究其对企业决策与绩效的影响;二是在不同竞争环境下,针对双渠道供应链的企业博弈行为进行对比研究.所以,本文在行为供应链管理优化研究领域具有较重要的理论价值.

2 基本模型

考虑双渠道供应链由一个电商平台和一个制造商组成.电商平台(如:京东)向制造商采购产品,并通过互联网向消费者进行产品销售,且依据市场需求情况向消费者制定定价决策.制造商(如:格力集团)生产相应产品,并通过两种销售渠道对产品进行销售:一是根据电商平台(如:京东)的订单为其提供产品;二是通过自身的网络销售渠道(如:格力董明珠店)进行销售.制造商根据两种销售渠道的需求情况向消费者制定定价决策.消费者在网购产品过程中可能会遭遇到产品质量、产品服务等各类问题,对消费者利益造成了损失,面对这些损失,不少消费者往往存在损失厌恶心理(如:对商家进行投诉、在网络上发布差评等),该心理对于网络销售市场产生重要影响.

以格力集团(制造商)生产的“3L大容量饭煲(型号:GDF-3019D)”产品为例,截至2021年4月24日,该产品在“格力董明珠店”(格力自建网络销售渠道)的价格为399元,好评率99%,累计销量为58288件.该产品在“京东”(电商平台)的价格为199元(仅限前200台),好评率98%,差评40+(例如:app提示货到了,我没有收到任何通知,不知道货在哪里? 煮饭速度慢,而且不好用;煮饭时间过长,口感不佳;盖子藏垢无法清洗等等).该产品在“天猫”(电商平台)的价格为279元,累计评价为1308条,其中差评2条.该产品在“苏宁易购”(电商平台)的价格为249元(仅限前100台),累计评价为4条,无差评.这表明,对于同一款产品而言,通过不同的网络渠道进行销售,电商平台和制造商制定的网络销售价格可能存在较大差异,这与企业所处的不同竞争环境,以及损失厌恶消费者市场密切相关.为了研究方便,本文提出以下几种假设:

H1:假定电商平台以其利润最大化为目标,从制造商采购产品,批发价格为w,通过付出相应成本,运营和维护网络销售平台,并利用网络销售平台向消费者销售产品,其网络销售成本为c,网络销售价格为pe,基于理性假设,应当满足条件pe-w-c>0.

H2:假定制造商以其利润最大化为目标,制造和生产产品,并付出相应的生产成本,同时,通过双渠道开展销售,一是向电商平台销售产品;二是自建网络销售渠道,并向消费者销售产品.令制造商的生产成本为j,网络销售价格为pm,网络销售成本为kc,其中,k表示制造商相对于电商平台的网络销售效率,如果k=1,则代表制造商的网络销售效率与电商平台的网络销售效率一致,k越大,表明相对于电商平台而言,制造商的网络销售效率越低,反之,制造商的网络销售效率越高.基于理性假设,应当满足条件pm-jkc>0,w-j>0,通常情况下,制造商批发产品获得的单位收益大于其网络销售产品获得的单位收益,即w-j>pm-j-kc.

H3:假定从生产制造到销售运输的各个环节都可能导致产品出现质量问题.因此,在网络购物过程中,消费者无法对产品的价值进行准确估计,这使得消费者可能遭受损失,且消费者存在损失厌恶心理,其损失厌恶系数为λ(λ>0).

根据H3,假设消费者在网络购物过程中,对某个网购产品的评估价值为v,该值服从密度函数为g(v),分布函数为G(v)的某个分布.如果评估价值v小于网络销售价格pe,pm,那么消费者存在损失,反之,消费者获得收益.基于此,根据前景理论[6]的核心思想,可以得到通过电商平台、制造商网络销售渠道进行网购的损失厌恶消费者效用函数分别为

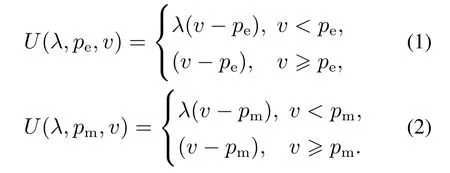
由式(1)和式(2)可以得到损失厌恶消费者的期望效用函数分别为

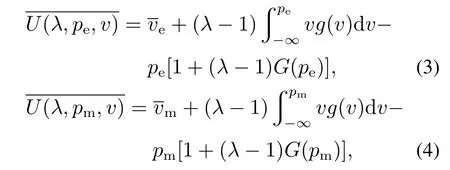
其中和分别表示消费者评估电商平台、制造商网络销售产品价值的平均值.

市场需求不仅与消费者的期望效用函数有关,而且还与竞争企业的网络销售价格有关.需要强调的是,制造商的需求量来自两个渠道,一是电商平台的需求量;二是自建网络销售渠道的需求量.借鉴文献[21],令电商平台与制造商的需求函数分别为

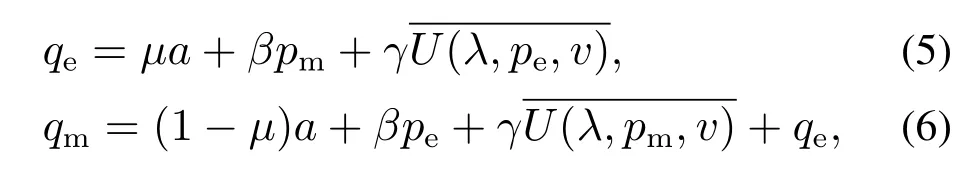
其中:a(a>0)表示基本需求,µ(0<µ<1)表示基本需求的电商平台份额,β(β >0)表示竞争企业的价格弹性系数,γ(γ >0)表示消费者期望效用的弹性系数,且γ >β,这是因为相较于其他渠道的销售价格而言,本渠道的需求量受到本渠道销售价格的影响更大.例如:若消费者打算在京东购买某款空调(格力制造),消费者更加关心的是该产品在京东的销售价格,而格力对该产品制定的销售价格只是作为参考.

根据H1和H2,可以得到电商平台和制造商的利润函数分别为

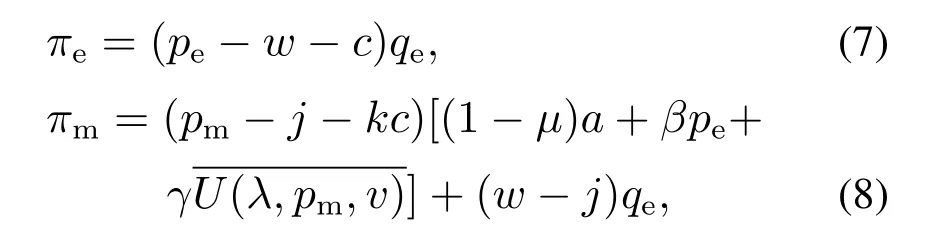
其中:πe表示电商平台利润;πm表示制造商利润.需要指出的是,制造商的利润来自两个方面,一是向电商平台批发产品获得的利润;二是在自建网络渠道向消费者销售产品获得的利润.

供应链利润由电商平台利润和制造商利润组成,因此,供应链的利润函数为

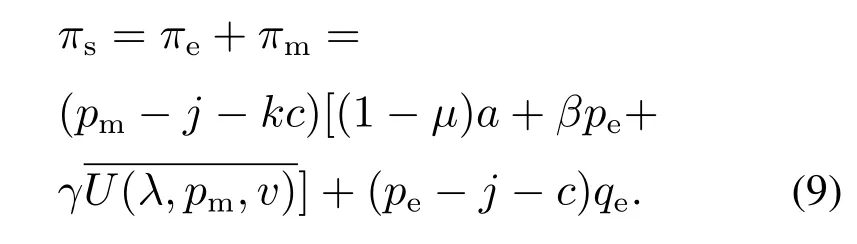
为了阐述方便,本文对以下符号进行特别说明:上标nd,sd1,sd2,cd分别代表Nash均衡博弈、制造商主导Stackelberg博弈、电商平台主导Stackelberg博弈与供应链集中.

3 不同竞争环境下的决策优化模型

3.1 Nash均衡博弈下的决策优化模型

在企业相互之间的博弈过程中,电商平台与制造商具有同等地位的网络销售主导权,它们进行Nash均衡博弈,在此环境下,电商平台与制造商同时开展网络销售价格决策.以苏宁易购与格力的价格竞争为例,价格竞争可能导致两败俱伤,在对方不改变价格的情形下既不能涨价,否则会缩小市场份额;也不能降价,这容易出现亏本抛售.于是两家公司可以改变之前的利益格局,通过谈判实现新的利益评估方案,分别选择自己的最优且稳定的价格决策,即Nash均衡博弈.下面根据Nash均衡博弈的思想,分别进行公式推导,得到电商平台与制造商的最优定价模型.

首先,将式(7)电商平台利润函数对电商平台网络销售价格pe分别求一阶导数和二阶导数,可以得到

其次,将式(8)制造商利润函数对制造商网络销售价格pm分别求一阶导数和二阶导数,可以得到

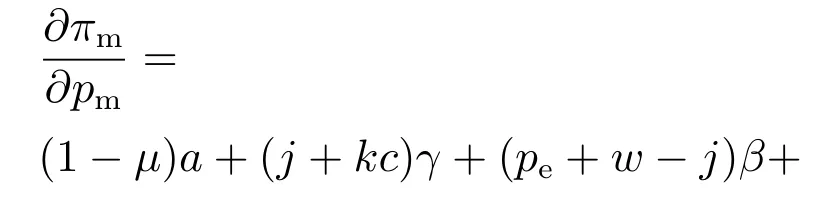
3.2 制造商主导Stackelberg博弈下的决策优化模型

在企业相互之间的博弈过程中,制造商在网络销售方面具有更强的主导权,而电商平台作为随从企业与制造商竞争,它们相互之间开展Stackelberg博弈.以京东与格力的价格竞争为例,在某些市场环境下,京东与格力企业之间的竞争地位往往不是对称的,而竞争地位的不对称导致企业决策次序的不对称.通常情况下,随从企业先观察到主导企业的行为,再决定自己的对策.主导企业知道随从企业一定会对它的决策作出反应.所以,当主导企业作出决策时,必须考虑随从企业的反应.

在制造商主导Stackelberg博弈下,制造商首先提出自己的网络销售价格,其次电商平台观察到制造商的网络销售价格之后制定自己的最优网络销售价格.根据Stackelberg博弈的特点,下面运用逆向归纳方法进行求解.

首先,将式(7)电商平台利润函数对电商平台网络销售价格pe分别求一阶导数和二阶导数,可以得到

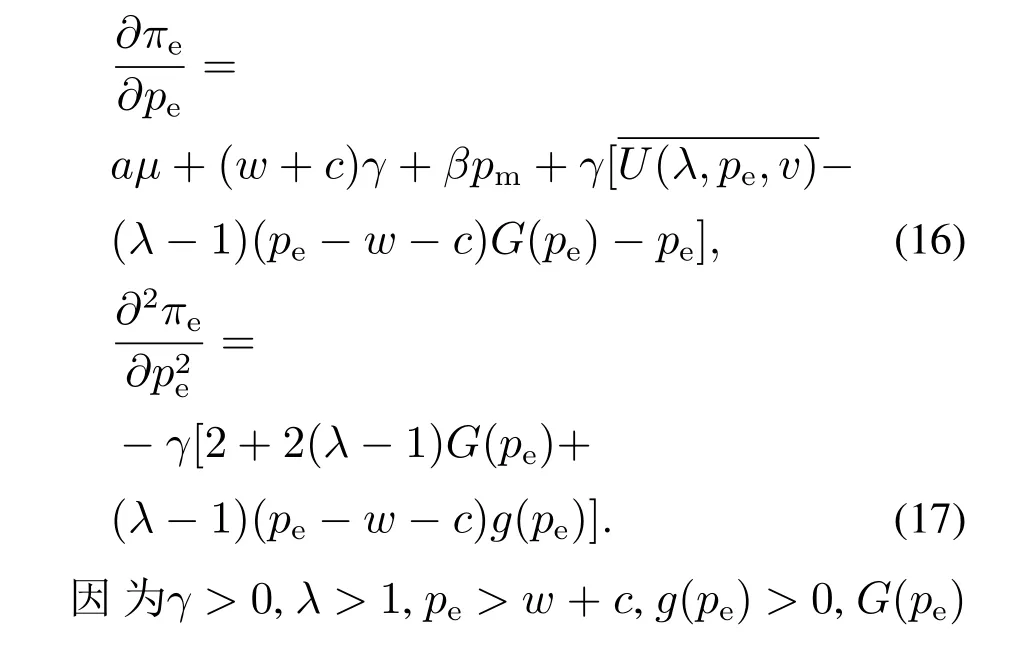
3.3 电商平台主导Stackelberg博弈下的决策优化模型

在企业相互之间的博弈过程中,电商平台在网络销售方面具有更强的主导权,制造商作为随从企业与电商平台竞争,它们之间开展Stackelberg博弈.以天猫与格力的价格竞争为例,天猫是电商平台的佼佼者,与天猫相比较,格力在网络销售领域并不占优势,这可能促使两家企业的决策次序存在区别.通常情况下,主导企业首先决定一个产品价格,随从企业观察到这个价格,然后根据这个价格决定自己的产品价格.需要强调的是,主导企业在决定自己的产品价格时,充分了解随从企业的反应.所以,主导企业会预期到自己决定的产品价格对随从企业的影响.也就是主导企业所决定的产品价格将是一个以随从企业的反应函数为约束的利润最大化的产品价格,而随从企业的价格决策不再需要自己的反应函数.

在电商平台主导Stackelberg博弈下,电商平台首先提出自身的最优网络销售价格,制造商在观察到电商平台的网络销售价格之后制定自己的最优网络销售价格.根据Stackelberg博弈的特点,接下来运用逆向归纳方法进行求解.

首先,将式(8)制造商利润函数对制造商网络销售价格pm分别求一阶导数和二阶导数,可以得到

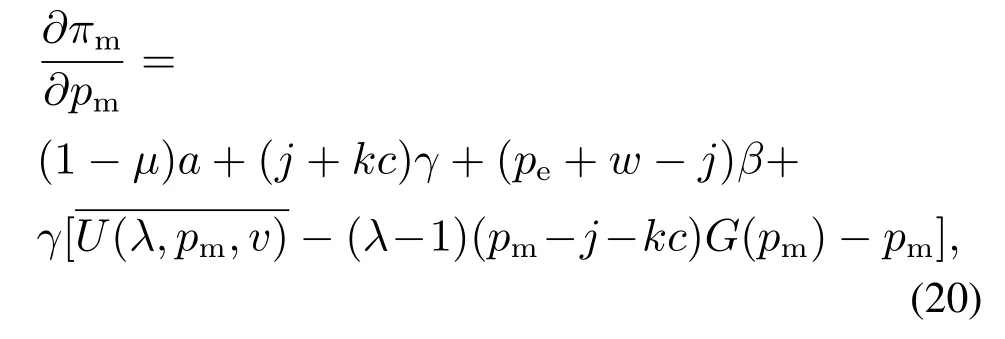
3.4 供应链集中下的决策优化模型

上述情形讨论的是分散式决策,即供应链中各个电商平台、制造商均以自身利益最大化为目标进行定价决策.而供应链集中下的决策是指企业决策者以供应链整体利益最大化为目标进行定价决策.举例而言,在供应链集中下,京东可以与格力达成战略合作,双方均以两家企业的整体利润最大化作为最终的决策目标,分别进行定价决策.

首先,将式(9)供应链利润函数对电商平台网络销售价格pe分别求一阶导数和二阶导数,可以得到

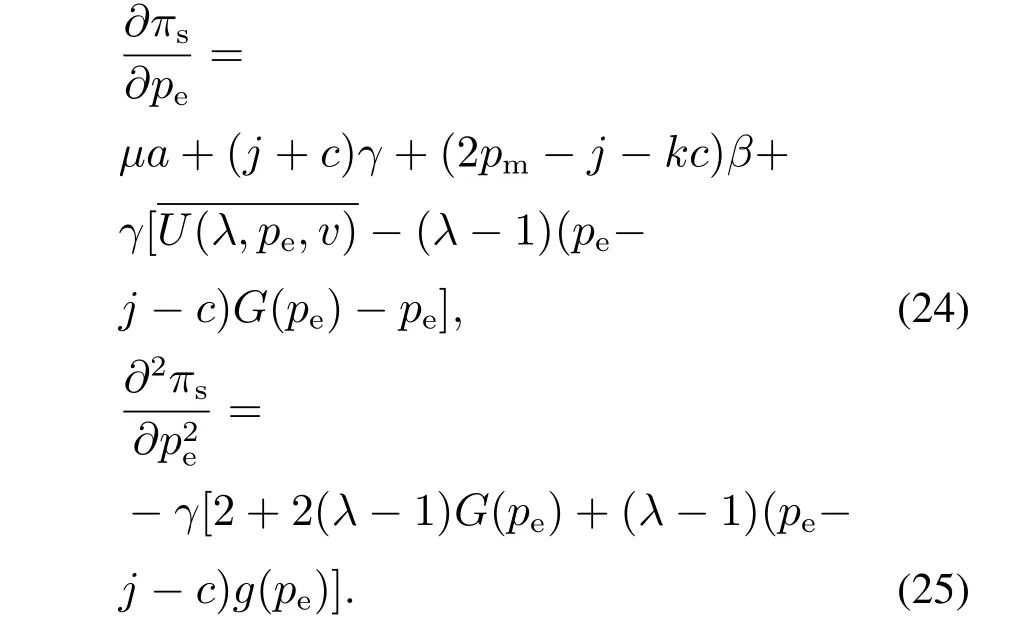
其次,将式(9)供应链利润函数对制造商网络销售价格pm分别求一阶导数和二阶导数,可以得到

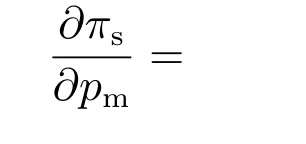
3.5 不同竞争环境下的决策优化模型分析

根据以上4种不同竞争环境下的供应链企业最优网络销售价格决策优化模型,下面通过对比的方式进行模型分析,可以得到命题1与命题2.

鉴于相关优化模型比较复杂,接下来通过算例分析进一步研究制造商的网络销售效率以及消费者的损失厌恶心理对企业决策优化与供应链收益的影响.

4 算例分析

假设某双渠道供应链由一个制造商(得力集团)和一个电商平台(京东)组成.制造商生产具体的产品(如:计算器),生产成本为j=2,且通过两个渠道销售产品,一是根据电商平台的订单向电商平台批发销售产品,批发价格为w=8;二是通过自建网络销售渠道(集什商城)向消费者销售产品.电商平台仅通过自身的网络渠道向消费者销售产品,其网络销售成本为c=1.消费者在网购过程中,对产品价值的评估值v服从均匀分布[1,30],且面对自身遭受的损失普遍存在损失厌恶心理,其损失厌恶系数为λ.网购市场的基本需求为a=10,基本需求的电商平台份额为µ=0.5,消费者期望效用的弹性系数为γ=5,竞争企业的价格弹性系数为β=1.通过Mathematica软件进行优化求解.1)取λ=2,分析制造商的网络销售效率k对企业定价与收益的影响,优化结果如表1所示;2)取k=8,分析消费者的损失厌恶系数λ对企业定价与收益的影响,优化结果如表2所示.

为了方便图形显示,令符号nd,sd1,sd2,cd分别代表Nash均衡博弈、制造商主导Stackelberg博弈、电商平台主导Stackelberg博弈与供应链集中情形.根据表1数据,可以得到图1-2.

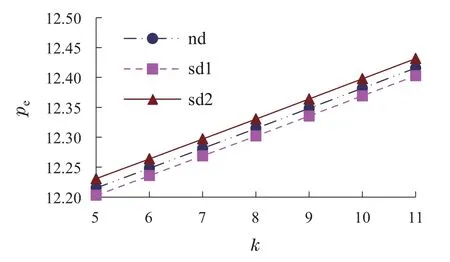
图1 pe与k的关系图Fig.1 The relationship between pe and k

由图1和图2可知,从企业定价的角度,在Nash均衡博弈、制造商主导Stackelberg博弈与电商平台主导Stackelberg博弈3种环境下,随着k的逐渐增大,电商平台与制造商的网络销售价格均呈现上升趋势.且通过比较表1的数据可知,电商平台与制造商的网络销售价格均在电商平台主导Stackelberg博弈下最大,均在制造商主导Stackelberg博弈下最小.这表明电商平台与制造商将通过提高网络销售价格来应对制造商网络销售效率的下降,这直接导致消费者的网购成本增大,且电商平台主导Stackelberg博弈进一步加大了该成本,而制造商主导Stackelberg博弈可以减少该成本.

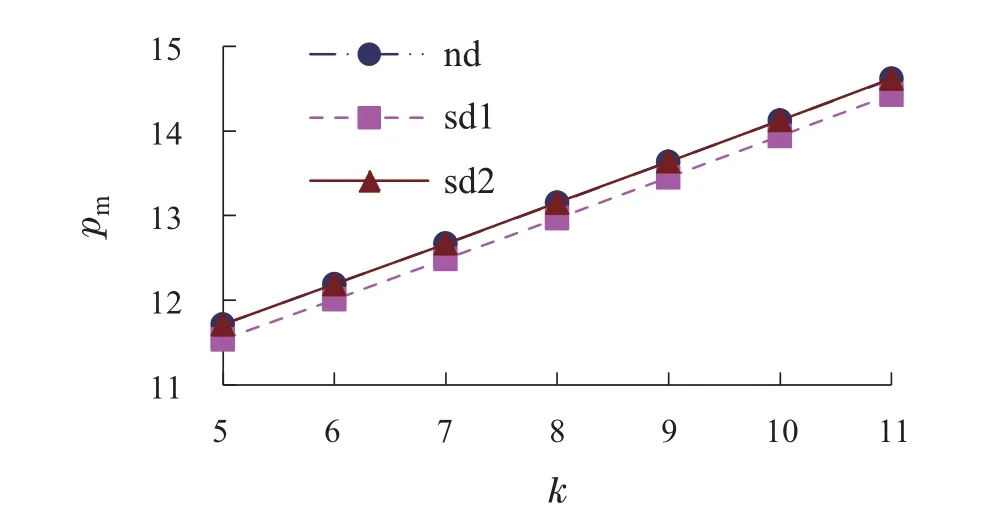
图2 pm与k的关系图Fig.2 The relationship between pm and k

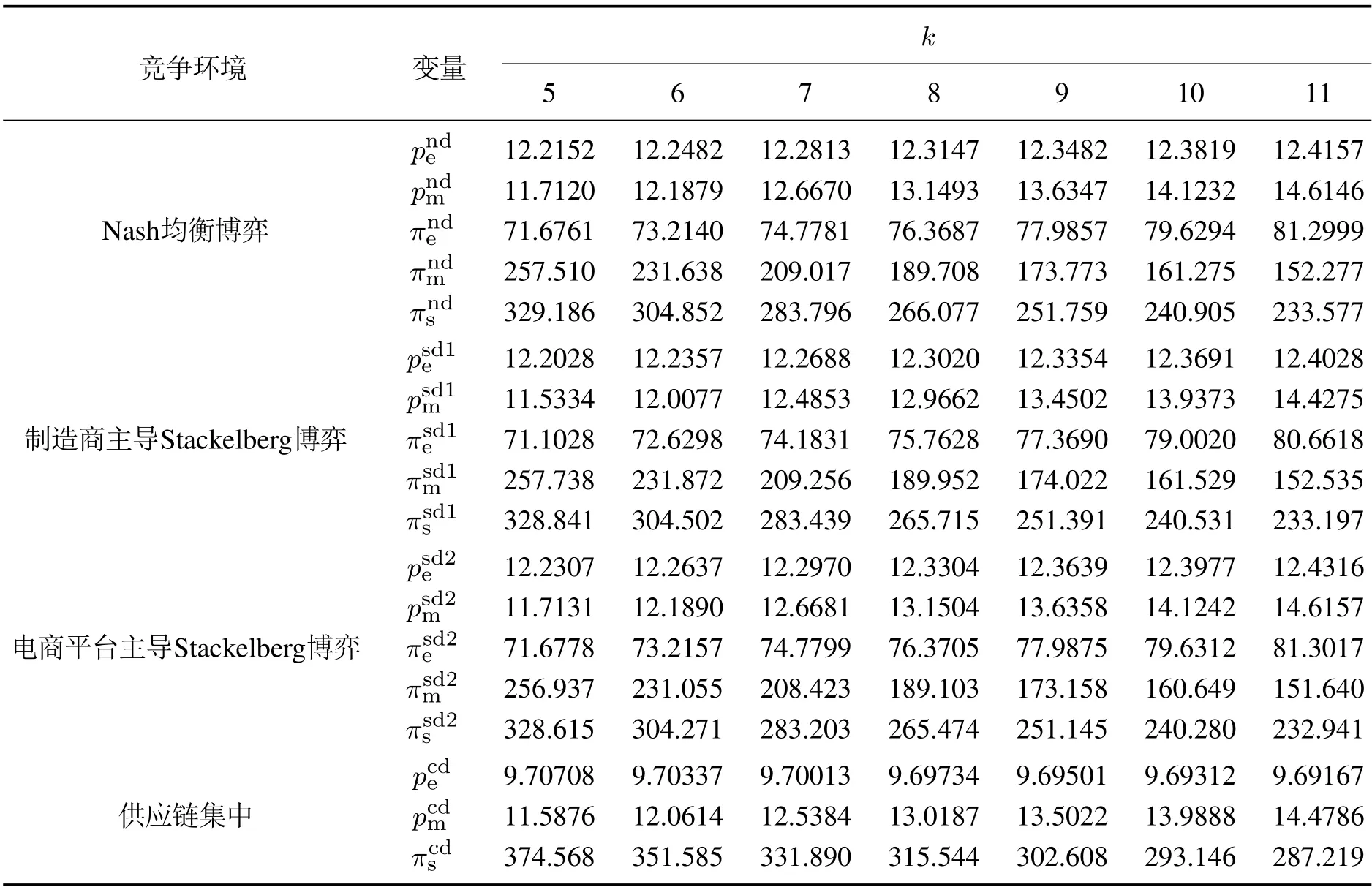
表1 k对企业定价与收益的影响Table 1 The impact of k on pricing and earnings

由表1数据可知,在供应链集中环境下,随着k的逐渐增大,电商平台与制造商的网络销售价格分别呈现下降和上升的趋势.

根据表1数据,可以得到图3-5.

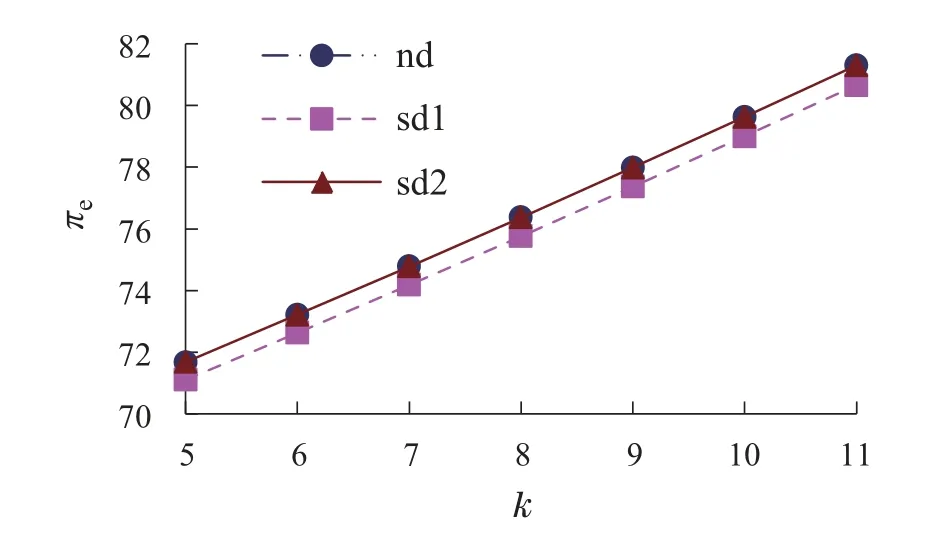
图3 πe与k的关系图Fig.3 The relationship between πe and k

由图3和图4可知,从企业收益的角度,在Nash均衡博弈、制造商主导Stackelberg博弈与电商平台主导Stackelberg博弈3种环境下,随着k的逐渐增大,电商平台收益与制造商收益分别呈现上升与下降的趋势.由图5可知,在这4种环境下,随着k的逐渐增大,供应链收益均呈现下降趋势,且在供应链集中下的供应链收益最大.通过比较表1的数据可知,在电商平台主导Stackelberg博弈下的供应链收益相对最小.这表明制造商的网络销售效率下降给制造商和供应链带来了负面影响,但有利于电商平台,且相对而言,电商平台主导Stackelberg博弈最不利于供应链绩效,而企业通过相互之间的合作能够促使供应链绩效改善.

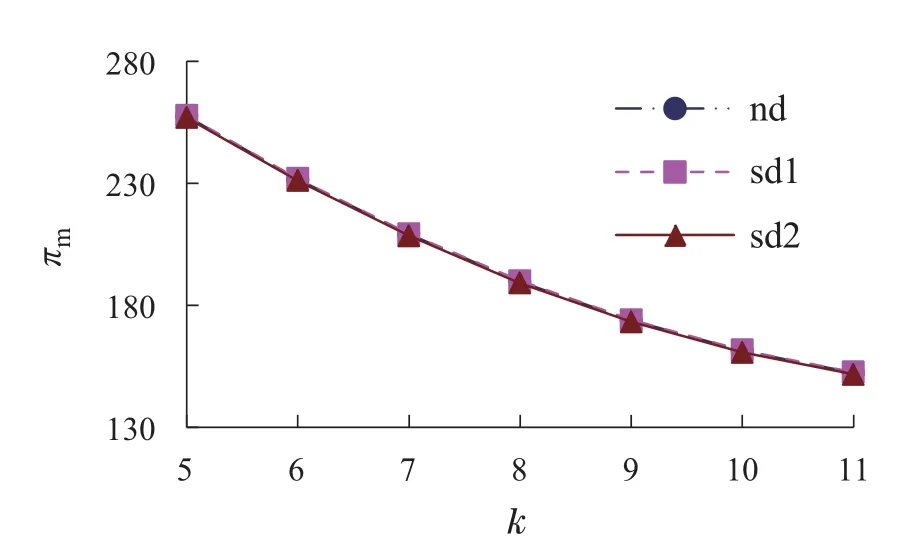
图4 πm与k的关系图Fig.4 The relationship between πm and k

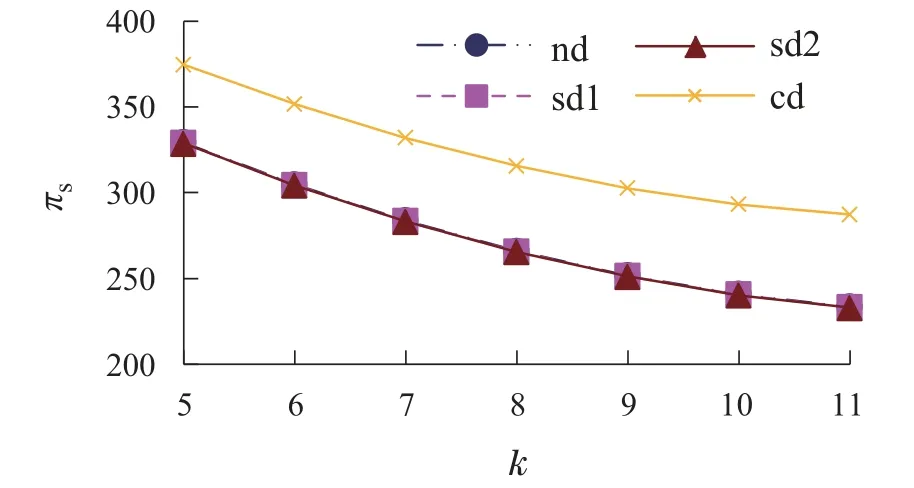
图5 πs与k的关系图Fig.5 The relationship between πs and k

根据表2数据,可以得到图6-7.

由图6和图7可知,从企业定价的角度,在Nash均衡博弈、制造商主导Stackelberg博弈、电商平台主导Stackelberg博弈和供应链集中4种环境下,随着λ的逐渐增加,电商平台和制造商的网络销售价格均呈现下降趋势.通过比较表2的数据可知,电商平台网络销售价格在电商平台主导Stackelberg博弈下相对最大,在供应链集中下最小;制造商网络销售价格也是在电商平台主导Stackelberg博弈下相对最大,但在制造商主导Stackelberg博弈下最小.这表明消费者在双渠道网购产品的过程中,其损失厌恶心理将导致企业网络销售价格下降,在电商平台主导Stackelberg博弈下,消费者的网购成本最大,在制造商主导Stackelberg博弈或供应链集中下,消费者的网购成本最小.

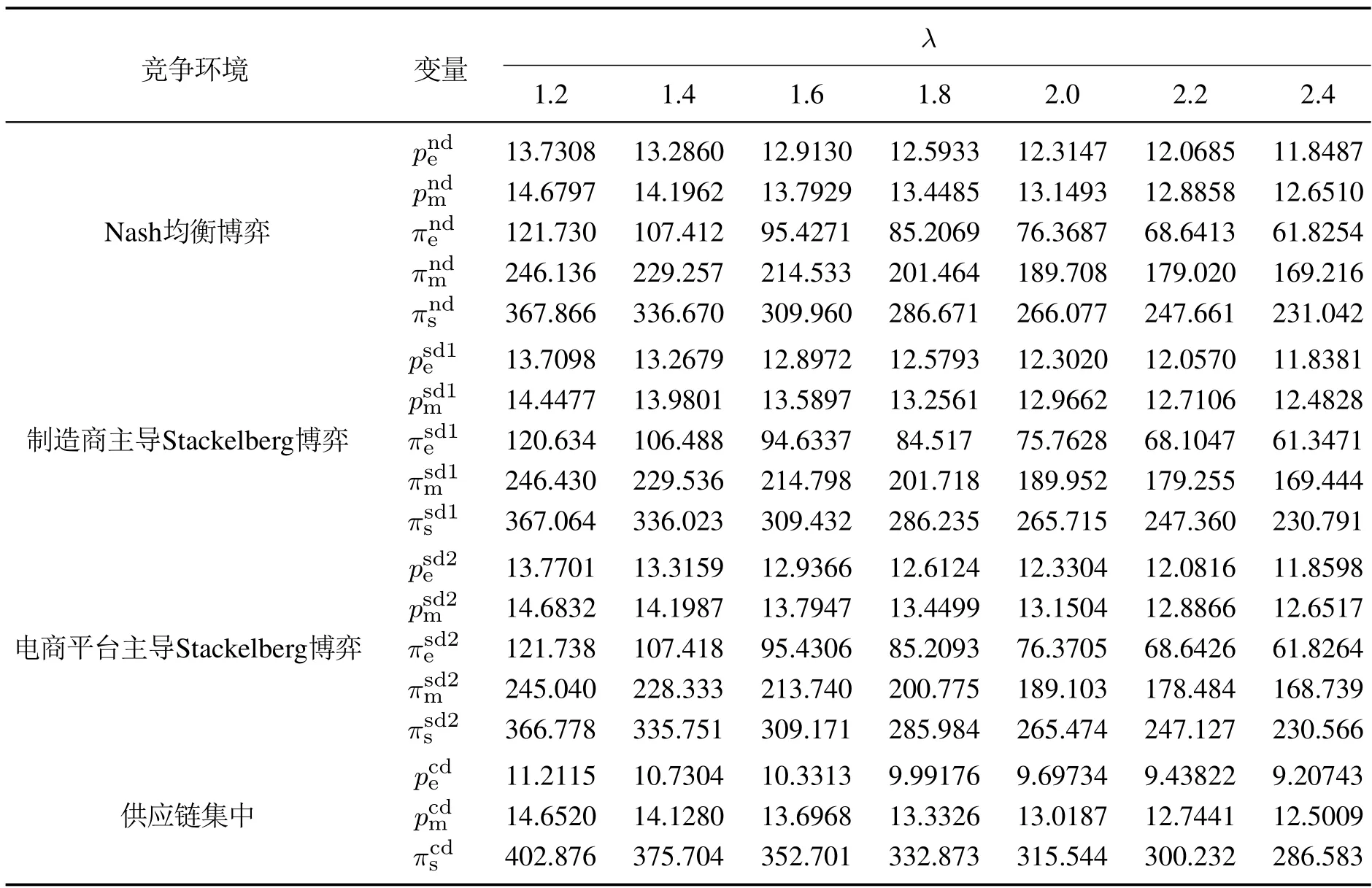
表2 λ对企业定价与收益的影响Table 2 The impact of λ on pricing and earnings

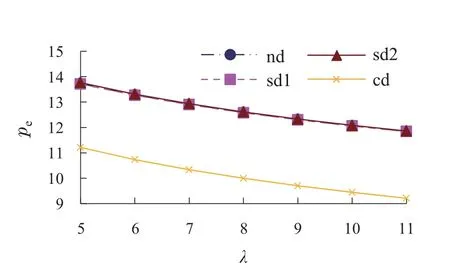
图6 pe与λ的关系图Fig.6 The relationship between pe and λ

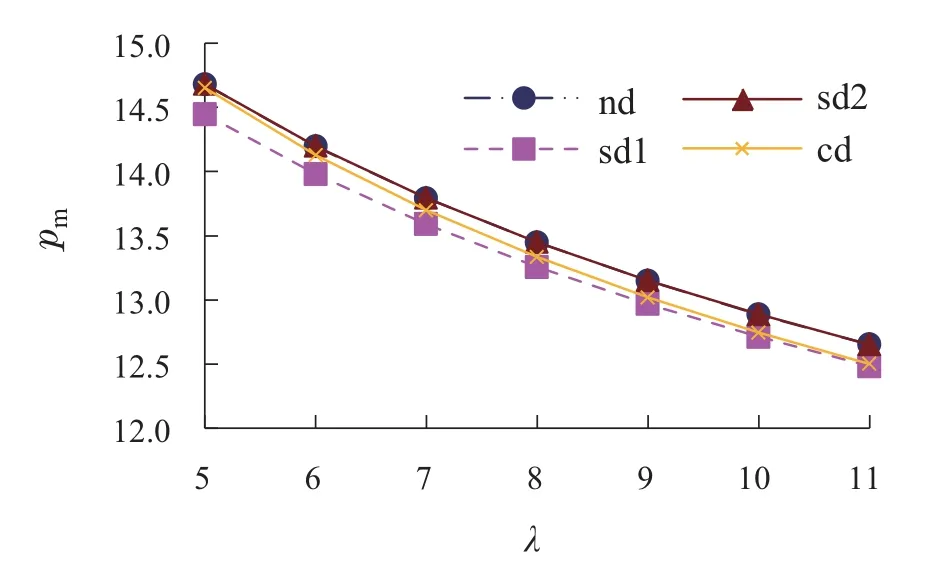
图7 pm与λ的关系图Fig.7 The relationship between pm and λ

根据表2数据,可以得到图8-10.

由图8-10可知,从企业收益的角度,在这4种环境下,随着λ的逐渐增加,企业与供应链的收益均呈现下降趋势.通过比较表2的数据可知,电商平台的收益在电商平台主导Stackelberg博弈下相对最大,在制造商主导Stackelberg博弈下相对最小;制造商的收益在制造商主导Stackelberg博弈下相对最大,在电商平台主导Stackelberg博弈下相对最小;且在供应链集中下供应链的收益最大,在电商平台主导Stackelberg博弈下供应链的收益相对最小.这表明消费者在双渠道网购产品的过程中,其损失厌恶心理对企业与供应链均带来负面影响,企业收益在自身企业主导Stackelberg博弈下最大,在对方企业主导Stackelberg 博弈下最小,电商平台主导Stackelberg博弈给供应链收益进一步造成了不利影响,而企业之间的相互合作能够缓解此不利影响.

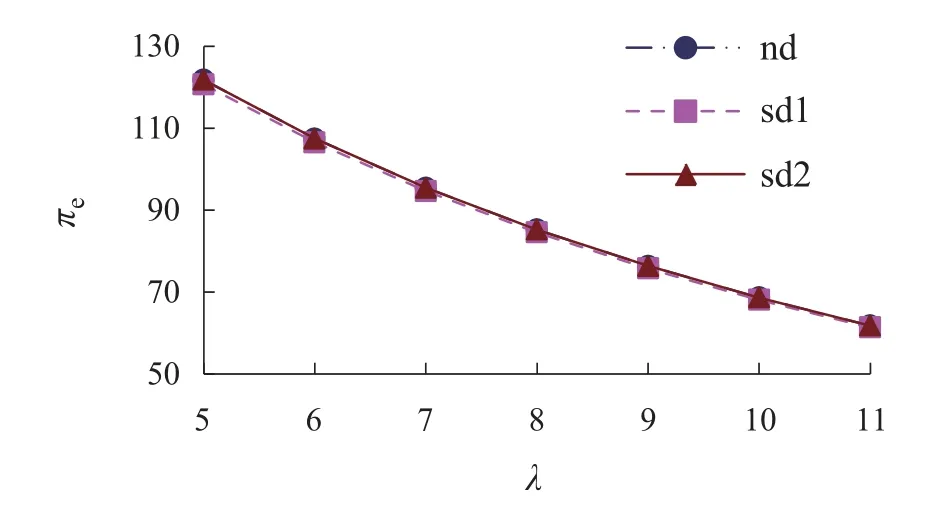
图8 πe与λ的关系图Fig.8 The relationship between πe and λ

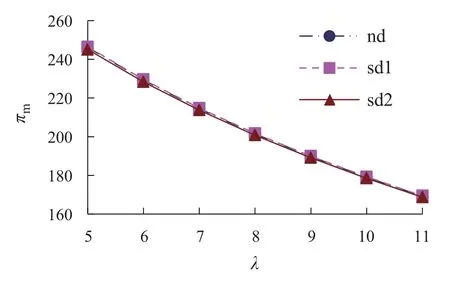
图9 πm与λ的关系图Fig.9 The relationship between πm and λ

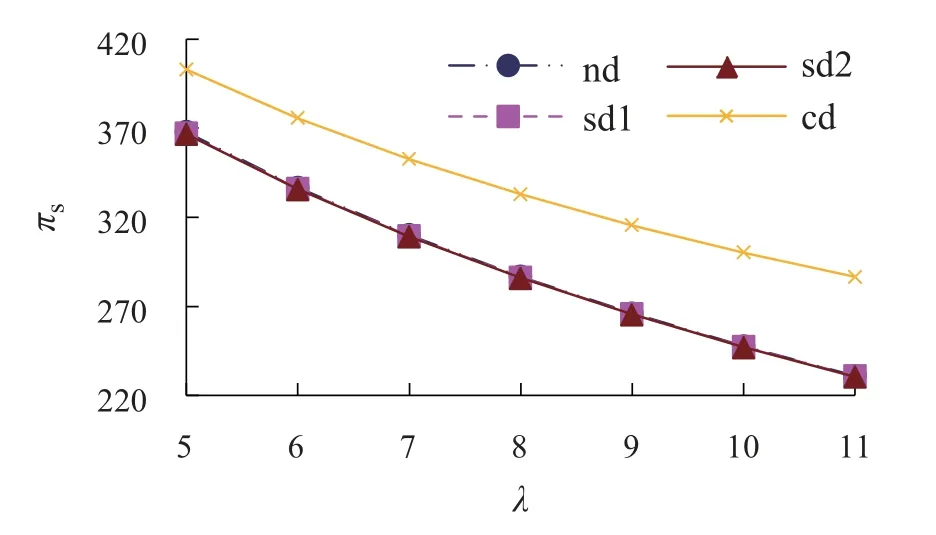
图10 πs与λ的关系图Fig.10 The relationship between πs and λ

5 结论

本文研究了电商平台与制造商开展网络销售的双渠道供应链,考虑制造商存在网络销售效率问题,消费者存在损失厌恶心理.在此基础上,分析了Nash均衡博弈、制造商主导Stackelberg博弈、电商平台主导Stackelberg博弈与供应链集中4种环境下电商平台与制造商的定价决策优化问题,主要结论如下:

1) 从消费者的角度.尽管制造商的网络销售效率下降不利于消费者降低网购成本,但可能促使在供应链集中下消费者通过电商平台网购的成本下降;消费者的损失厌恶心理促使网络销售价格下降,且电商平台主导Stackelberg博弈下的网络销售价格最大,制造商主导Stackelberg博弈或供应链集中下的网络销售价格最小.所以,消费者在制造商的网络销售效率较高,且制造商与电商平台相互合作的环境中网购产品,并通过提高自己的损失厌恶心理来获取更大的收益.

2) 从电商平台的角度.制造商的网络销售效率下降促使电商平台收益提高;消费者的损失厌恶心理导致电商平台收益下降,且电商平台收益在制造商主导Stackelberg博弈下最小.所以,制造商较低的网络销售效率对电商平台是有利的,电商平台尽量规避在具有较强实力的制造商,以及损失厌恶型消费者主导的市场环境下经营.

3) 从制造商的角度.制造商的网络销售效率下降导致制造商收益下滑,消费者的损失厌恶心理进一步加剧了制造商收益下降,且制造商收益在电商平台主导Stackelberg博弈下最小.所以,制造商应当努力提高自身的网络销售效率,尽量规避在具有较强实力的电商平台,以及损失厌恶型消费者主导的市场环境下经营.

4) 从供应链的角度.制造商的网络销售效率下降导致供应链收益下滑,消费者的损失厌恶心理也将导致供应链收益下降,且供应链收益在供应链集中下最大,在电商平台主导Stackelberg博弈下最小.所以,通过提高制造商的网络销售效率,促进企业相互合作能够提升供应链收益,但电商平台具有较强的实力,以及损失厌恶型消费者主导的市场环境对供应链是不利的.

针对网络销售效率和损失厌恶心理的双渠道供应链网络定价决策优化问题,本文提出了具有一定参考价值的结论.但是只考虑了消费者存在损失厌恶心理,没有考虑企业也可能存在损失厌恶心理,以及网络订货决策的优化问题,这些是后续值得研究的方向.