基于等价输入干扰补偿的改进型重复控制系统参数优化设计

廖常超 ,周 兰 ,潘昌忠 ,陈 静

(1.湖南科技大学信息与电气工程学院,湖南湘潭 411201;2.湖南科技大学数学与计算科学学院,湖南湘潭 411201)

1 引言

在工程实践中,许多系统需要完成周期性的控制任务,例如直流双馈感应发电机对周期性转矩波动的抑制[1]、永磁同步电机伺服系统的电流控制[2]、逆变器电压控制[3]等.重复控制为解决这些周期信号跟踪/抑制问题提供了有效的方法,其理论基础是内模原理[4],通过将周期信号的内部模型植入到稳定的闭环系统中,实现对周期为Tr的任意目标信号无偏差的稳态跟踪/抑制.基本重复控制系统是一个中立型时滞系统,为了放宽系统的稳定性条件,需要在时滞环节嵌入低通滤波器,构造改进型重复控制器[5].然而,改进型重复控制器只是周期信号的近似模型,系统的稳态跟踪误差不再为零.因此,改进型重复控制系统存在稳定性和跟踪性能之间的折衷问题.如何同时优化低通滤波器的截止频率和镇定控制器参数是解决这个折衷问题的关键.

目前,大部分重复控制系统设计方法通常预先设定低通滤波器截止频率,忽略了截止频率与控制器参数之间的关系,从而使得系统性能的改善受限.DOH等人针对已设计好镇定控制器的不确定线性系统,提出基于线性矩阵不等式(linear matrix inequality,LMI)的重复控制器设计方法[6],但低通滤波器截止频率的选取需要反复试凑才能获得比较理想的控制效果.文献[7]提出基于LMI的低通滤波器参数和状态反馈增益优化方法,但采用固定权重的LMI求解控制器参数具有较大的保守性.文献[8]提出一种基于二维混合模型的改进型重复控制系统迭代优化设计算法,对低通滤波器截止频率和状态反馈控制器参数的同时优化,减少了由LMI方法带来的保守性,然而该方法需要系统状态完全可测.

重复控制方法对周期信号有着良好的控制性能,然而,由Bode积分定理[9],重复控制系统在周期信号的基波及其谐波频率处的增益很大导致其在其他频率处的增益减小,从而降低了系统的非周期控制性能.为了提高重复控制系统的非周期扰动抑制性能,有学者提出了自适应重复控制[10]、滑模重复控制[11]和H∞重复控制[12]等方法,这类方法主要通过提高控制器本身的鲁棒性以降低扰动在系统输出通道的灵敏度,被视为被动扰动抑制方法.在这类单自由度反馈控制系统中存在一些固有的性能约束,其中较为突出的是标称性能与鲁棒性、跟踪性能与扰动抑制性能之间的折衷问题[13].

主动扰动抑制方法建立的控制系统具有两个自由度,其中一个自由度用于改善系统的扰动抑制性能,另一个自由度用于使系统达到期望的控制性能.目前,这种主动抑制方法已被应用于重复控制系统设计,如基于自抗扰的重复控制[14-15]、基于扰动观测器的重复控制[16]和基于等价输入干扰(equivalent input disturbance,EID)的重复控制[17-20]等.其中,自抗扰的方法需要将控制对象重构为具有匹配型总扰动的积分器串联形式[21],利用扩张状态观测器对总扰动进行估计与补偿.这种转化通常需要对扰动项、输出或输入项进行求导,导致扰动被放大,并且可能会影响系统的稳定[22].扰动观测器方法需要利用系统的逆模型来构造扰动估计器,当被控对象具有不稳定零点或极点时,使用逆模型会引起不稳定的零极点对消,从而破坏系统的内部稳定性.

EID方法是SHE等人提出的一种主动扰动抑制方法[17],其基本思想是根据扰动对系统输出的影响效果,定义一个与外界扰动等价的输入端干扰(EID),通过在输入通道引入这个EID估计来抵消外界扰动对系统输出的影响.EID估计可以直接由状态观测器得到,无需利用系统的逆模型.它可以补偿匹配或非匹配等各种类型扰动,不需要扰动的先验信息.EID方法的关键是设计能够快速、精确估计EID的估计器.同时,为了消除高频噪声对系统输出的影响,通常在EID估计器中引入低通滤波器,然后将滤波后的EID估计反馈补偿到输入端.EID估计器中低通滤波器截止频率的选择对系统抗干扰性能有着显著的影响[17],然而目前大多数文献都是选择固定的低通滤波器截止频率,这在一定程度上限制了扰动抑制性能的改善.实际上,截止频率越高,系统的抗扰性能越好,但太高的截止频率会让高频噪声通过,起不到滤波的效果.截止频率太小则会过滤掉有用的低频信号,而且造成相位滞后,导致系统抗扰性能不好.

为了解决上述问题,本文针对一类含有非匹配扰动的伺服系统,提出基于EID补偿的改进型重复控制系统参数优化设计方法.通过在改进型重复控制系统中引入EID方法,构造基于EID补偿的系统结构.引入一个对系统抗扰性能、跟踪性能和收敛速度进行整体评价的综合性能指标,作为粒子群优化(particle swarm optimization,PSO)算法的适应度函数,相应的权值系数分别表征抗扰性能、跟踪性能和过渡过程性能所占的比重,以系统稳定性条件为目标约束条件,建立系统参数优化模型,实现对重复控制器前馈增益、低通滤波器截止频率、状态观测器增益、状态反馈控制增益和EID估计器内低通滤波器截止频率的同步优化,使得系统同时具有满意的扰动抑制性能、动态性能和稳态跟踪性能.数值仿真验证了所提方法的有效性.

2 系统描述

考虑如下受扰单输入单输出系统:

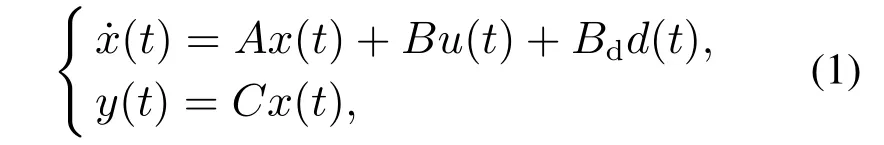
其中:x(t)∈Rn为系统状态变量,u(t)∈R为控制输入,y(t)∈R为系统输出,d(t)表示外部扰动,A,B,Bd,C为具有合适维数的已知实数矩阵.

假设1系统(1)中(A,B)能控、(A,C)能观,且在虚轴上没有零点.

注1假设1是伺服系统设计的标准条件,以保证其内部稳定性.此外,系统能观是设计状态观测器的前提.

注2系统(1)中若矩阵B和Bd的秩满足rank(B,Bd)=rank(B),即B=λBd,λ ∈R,则扰动d(t)与控制输入u(t)在同一通道,属于匹配型扰动,否则为非匹配型扰动.

基于EID补偿的改进型重复控制系统结构框图如图1所示.

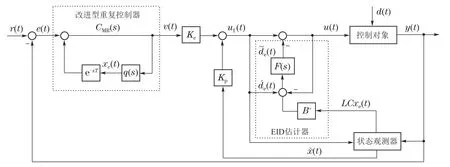
图1 基于EID补偿的改进型重复控制系统结构Fig.1 Configuration of EID-compensation based modified repetitive control system

EID方法的思路是首先将系统外部干扰对系统输出的影响等效为一个控制输入端的虚拟信号,即EIDde(t),然后采用全维状态观测器对de(t)进行估计,引入低通滤波器,构造EID估计器,并将滤波后的EID估计值(t)反馈补偿到控制输入端,建立复合重复控制规律.

2.1 EID估计器

假设2系统(1)中扰动d(t)引起的输出轨迹y(t)∈Φ,其中Φ=pi(t)sin(ωit+φi),i=1,2,···,n<∞,ωi(≥0)和φi为常值,pi(t)为与时间有关的多项式函数.

假设2是合理的且符合实际的.如果扰动d(t)引起的输出轨迹y(t)∈Φ,则由稳定逆的概念可以得出,在产生相同轨迹的控制输入通道上必然存在一个EIDde(t)∈Φ.

引理1在假设1成立的情况下,系统(1)存在一个作用于控制输入通道的EIDde(t),其对系统输出的影响与外部扰动d(t)的作用等效[17].

根据引理1,可以将系统(1)表示为

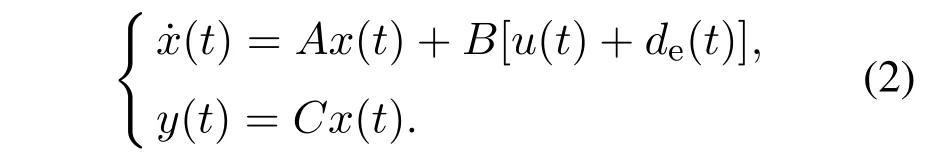
设计全维状态观测器

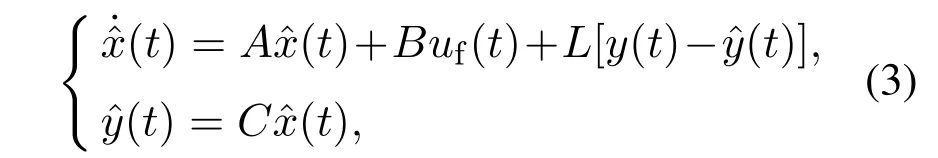
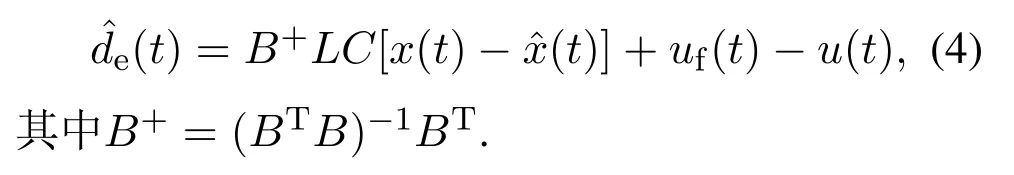
注3通过全维状态观测器(3)估计系统状态,利用系统实际状态与全维状态观测器状态之间的差值表示EID估计值.与自抗扰控制(active disturbance rejection control,ADRC)方法不同,EID方法不关注扰动本身,而是关注扰动对输出的影响.更具体地说,EID方法实质是引入一个与实际扰动对系统输出具有相同影响的虚拟控制输入信号EIDde(t),并对其进行估计与补偿,因此EID方法可以同时处理匹配扰动与非匹配扰动.另一方面,从控制输入端估计扰动对系统输出的影响比估计扰动本身更合理.

2.2 改进型重复控制器

设参考输入r(t)的周期为Tr,基本重复控制器的传递函数为

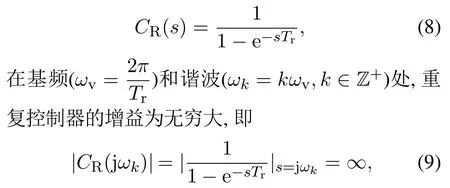
从而基本重复控制系统对该周期信号能够实现无稳态偏差跟踪.图1中的改进型重复控制器传递函数为

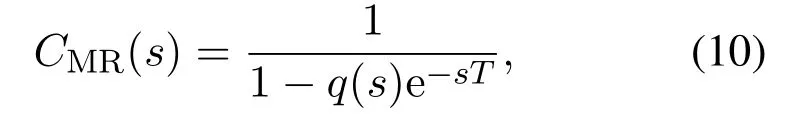
其中T为改进型重复控制器的时滞常数,q(s)为一阶低通滤波器

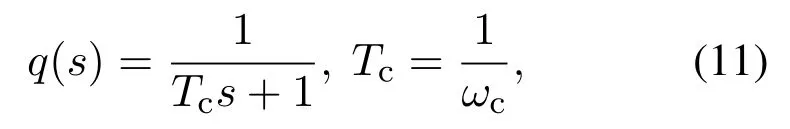
式中ωc是滤波器的截止频率,其取值遵循以下频率特性[5]:

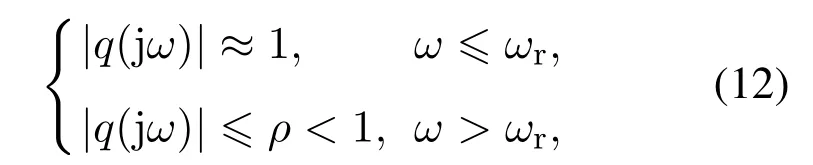
式中ωr为周期性参考输入r(t)的最大角频率.一般地,为了获得较好的控制性能,滤波器的截止频率须满足ωc≥5ωr.改进型重复控制器的状态空间模型为

其中:xc(t)为低通滤波器状态变量,v(t)为重复控制器的输出,e(t)=r(t)-y(t)为跟踪误差.

改进型重复控制器只是周期信号发生器的近似模型,低通滤波器q(s)的引入降低了重复控制器在周期信号基频和谐波处的增益.设T=Tr=2π,分别取ωc=1000和ωc=10时,改进型重复控制器的对数幅频特性曲线如图2所示.由图2可知,当ωc=1000时,在周期信号的基波和2次谐波处的增益分别为98 dB和86 dB;当ωc=10时,在周期信号的基波和2次谐波处的增益则降至为46.4 dB和34.5 dB.因此,为了提高重复控制系统的稳态控制精度,需要尽可能地提高低通滤波器的截止频率.

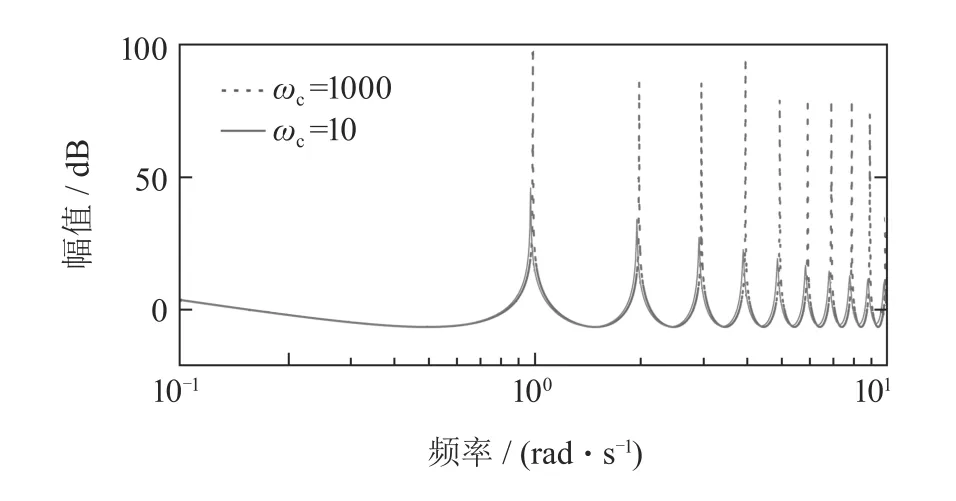
图2 不同截止频率下的|CMR(jω)|伯德图Fig.2 |CMR(jω)|Bode plots at different cutoff frequencies

关于改进型重复控制器时滞常数T的选取,通常情况下设置为与参考信号r(t)的周期Tr相同.然而,低通滤波器的嵌入造成相位滞后,使得重复控制器实际上在略小于基频和谐波处取得最大增益值.为了提高系统对周期信号的跟踪性能,保证改进型重复控制器在基频和谐波处取得最大增益值,需要对时滞常数T进行校正.

如图3所示,校正后的改进型重复控制器在周期信号的基频和谐波处增益能够取得极大值.

基于重构状态反馈的重复控制规律为

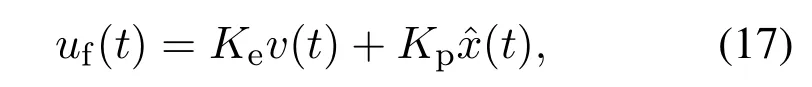
其中Ke和Kp=[Kp1Kp2··· Kpn]分别为重复控制器前馈增益和状态反馈控制增益.

2.3 基于EID补偿的复合重复控制规律

将滤波后的EID估计反馈补偿到控制输入端,构造基于EID补偿的复合重复控制规律

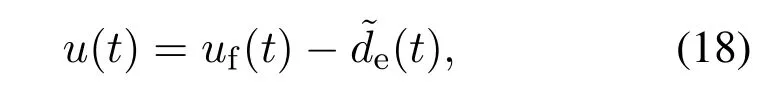
其中:Ke和Kp用于提高系统的跟踪响应速度和稳定性,EID估计(t)直接引入到复合控制输入中,用以消除扰动d(t)对输出y(t)的影响.EID估计的精度直接关系到扰动抑制性能,重复控制器参数的选取,直接关系到系统的周期信号跟踪性能.因此,本文控制设计的目的是,选择EID估计器和重复控制器参数的最优组合,使得系统在复合重复控制律(18)作用下稳定,并且同时获得满意的跟踪性能和扰动抑制性能.

3 稳定性分析及系统参数优化设计

本节首先对系统(图1)进行结构等价变换,然后分析系统的稳定性,最后给出系统参数优化设计算法.

3.1 稳定性分析

外部输入信号与线性系统的稳定性无关.令

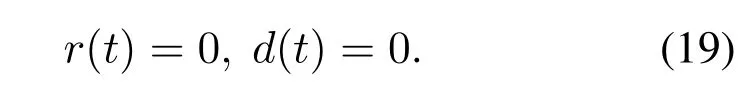
系统(1)就变成

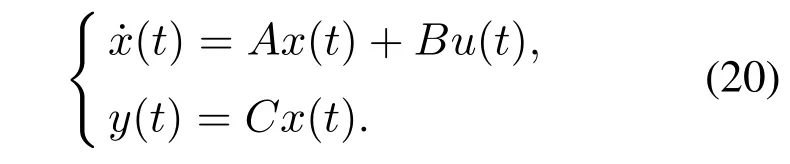
定义状态估计误差变量

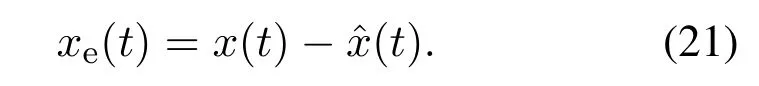
由式(3)(18)(20)-(21)得到

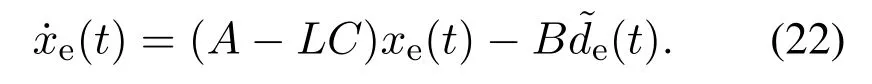
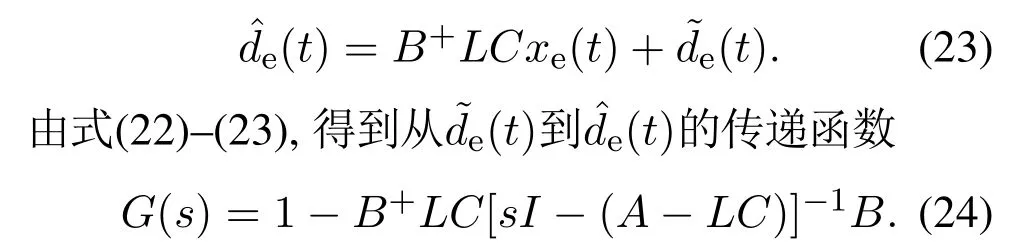
式(4)可重新表示为由式(24)可以看出,重复控制器的参数对EID估计器没有影响.将图1所示的系统进行结构等价变换,得到等效系统(如图4),它由两个子系统组成:基于状态反馈的改进型重复控制子系统1和包含状态观测器和EID估计器的子系统2.

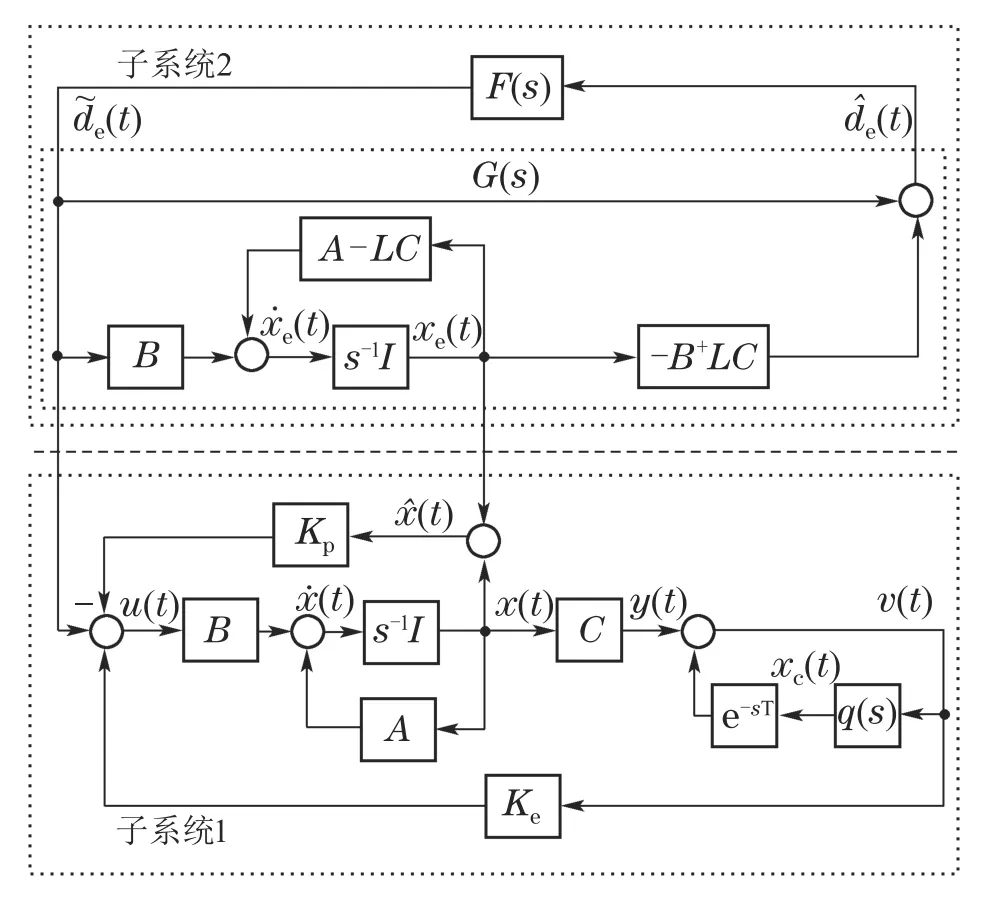
图4 图1的等价系统Fig.4 Equivalent system of Fig.1

不考虑重复控制器的嵌入,在子系统1中,从u(t)到y(t)的传递函数为

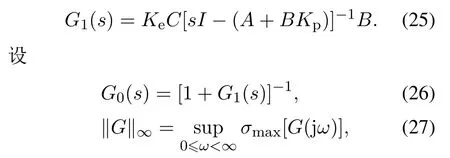
其中σmax[·]表示最大奇异值.G(jω)=G(s)|s=jω.

定理1如果系统(1)满足假设1,并且以下条件同时成立:

则图1所示的基于EID补偿的改进型重复控制系统在复合控制律(18)作用下渐近稳定.

证由于基于EID的改进型重复控制系统可以分解成两个串联的子系统(子系统1和子系统2),由分离定理[23]知,整个系统的稳定等价于两个子系统同时稳定.根据小增益定理,如果条件(a)和条件(c)同时满足,则子系统1稳定.对于子系统2,该系统是一个包含状态观测器和EID估计器的系统.显然,若条件(b)和条件(d)同时满足,则子系统2稳定.

证毕.

3.2 基于粒子群优化算法的系统参数设计

粒子群优化(particle swarm optimization,PSO)算法是一种群体智能算法,其思想来源于对鸟群觅食过程的模拟,通过种群粒子之间的信息交互相互协作完成食物的搜寻[24].本节利用PSO算法对式(17)中的Ke和Kp、观测器(3)中的L、低通滤波器(5)中的ωq和低通滤波器(11)中的ωc进行同步优化.在迭代过程中,粒子的速度与位置更新公式为

其中:K为最大迭代次数,wmax和wmin分别代表了最大和最小的惯性权重,惯性权重w在前期较大可加强全局搜索能力,w后期较小可加强局部搜索能力.

定义目标函数

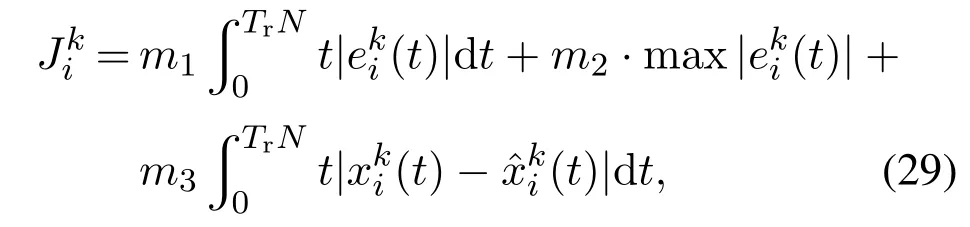
作为PSO算法的适应度函数,对系统的稳态性能、暂态性能和扰动抑制性能进行总体评价.具体地,式中第1项为时间与跟踪偏差绝对值乘积的积分,主要评价系统的动态性能和稳态性能;第2项为最大跟踪误差的绝对值,防止系统超调量过大问题,主要评价系统的暂态性能;最后1项为时间与状态估计偏差绝对值乘积的积分,主要评价系统的扰动抑制能力.m1,m2和m3分别为各项对应的权值,N为重复控制周期的个数,Ji,ei(t)分别为第i个粒子对应的适应度值和系统跟踪误差,xi(t)和(t)分别为第i个粒子对应的状态变量以及状态变量的估计值.

注5式(29)第1项和第3项中的时间因子t用来降低可能存在初始大误差对性能指标的影响,同时强调了过渡过程后期的误差对指标的影响,着重惩罚过渡过程过长.

本文的优化设计目的是以系统的稳定性条件为目标约束条件,建立综合评价系统抗扰性能、过渡过程性能和周期信号跟踪性能的目标函数,采用PSO算法搜索使得目标函数最小的系统最优控制器参数组合.

注6为了防止粒子群算法中的粒子出现“漫游”(超出搜索范围)和“速度爆炸”(速度无限增大)而导致粒子出现发散无法全局收敛的问题,迭代过程中粒子的位置和速度一旦超过设置的边界值,则将其值限定为边界值.除此之外,为了提高PSO种群的多样性,防止粒子陷入局部最优,粒子每完成一次迭代,算法重新对粒子的位置和速度进行了随机初始化,从而保证粒子收敛到全局最优位置.更为详细理论分析请参考文献[25-26].

4 数值仿真

双电机耦合伺服系统在数控机床、混合电动汽车等领域有着广泛的应用.在本节中,将本文所提方法应用于双电机耦合伺服系统的转速控制问题.该系统包含两个电机:一个用作控制对象,另一个作为扰动发生器产生转矩扰动,其中转矩扰动从控制输入通道以外的通道施加到受控电机上,两个电机的轴用联轴器连接在一起.系统模型为[17]

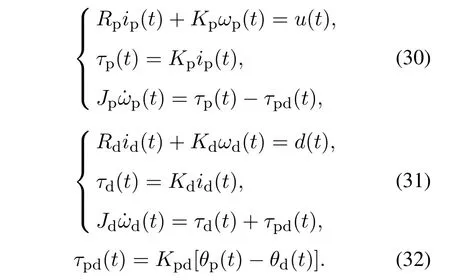
在式(30)-(32)中下标为p(或d)的变量和参数表示它们与被控电机(扰动发生器)有关,其中u为受控电机的电压,d为加于扰动发生器的电压,ip(id)为电枢电流,τp(τd)为转矩,τpd为扭转力矩,ωp(ωd)为旋转角速度,θp(θd)为旋转角度,Jp(Jd)为转动惯量,Rp(Rd)为电枢电阻,Kp(Kd)为反电动势常数,Kpd为联轴器扭转弹性系数.

选取系统输出为y(t)=ωp(t),系统状态为

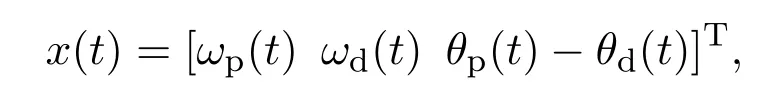
由式(30)-(32)建立系统(1)形式的双电机耦合伺服系统状态空间模型,其对应的系数矩阵为

显然,d1(t)是周期为Tr的扰动信号,d2(t)是周期不为Tr的扰动信号,d3(t)为非周期扰动信号.

注意到rank(B,Bd)>rank(B),因此式(35)d(t)为非匹配扰动.

4.1 控制器参数整定与系统仿真

根据实际控制对象的工作情况,选择PSO算法相关参数:粒子数n=20,最大迭代次数K=20,搜索维度d=9(即优化参数个数),学习因子c1=1.45,c2=1.45,惯性权重wmax=0.9,wmin=0.4,目标函数各项权重为m1=0.6,m2=1,m3=0.2,重复控制周期个数N=25.控制器参数搜索范围如下所示:

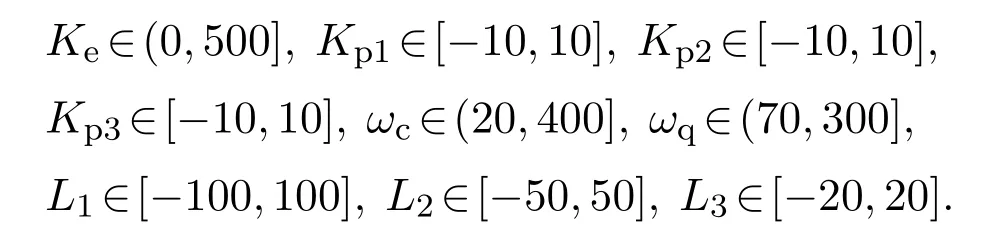
利用PSO算法得到的控制器参数分别为

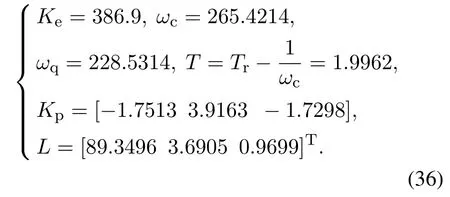
经过简单的计算可得

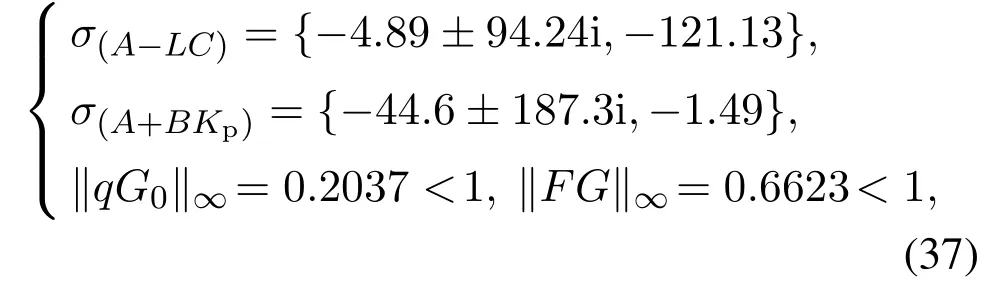
其中σ(·)表示特征根集合,优化得到的控制器参数全部满足定理1中的4个条件,从而图1所示的基于EID补偿的改进型重复控制系统是稳定的.

图5为本文提出的基于EID补偿的改进型重复控制系统参数优化设计方法(PSO-EID-MRC)在控制器参数(36)下的仿真结果,从图中可发现系统输出能够快速、准确地跟踪周期参考输入信号r(t),3个周期后系统进入稳态.在20 s受到一个非周期外部扰动,EID估计器可以快速准确地补偿外部扰动对输出的影响,系统跟踪误差波动较小,约2个周期后重新恢复稳态,最大稳态跟踪误差为5.152×10−5,系统具有良好的扰动抑制性能.实际扰动d(t)、EID估计值(t)曲线分别如图6-7所示.

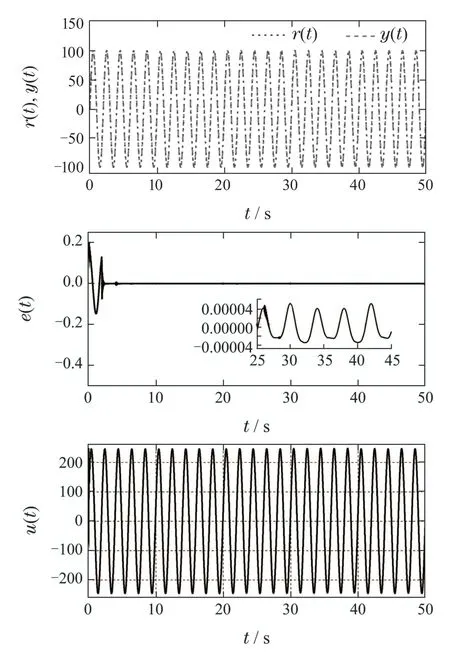
图5 基于PSO-EID-MRC方法系统输出响应Fig.5 System output response based on PSO-EID-MRC

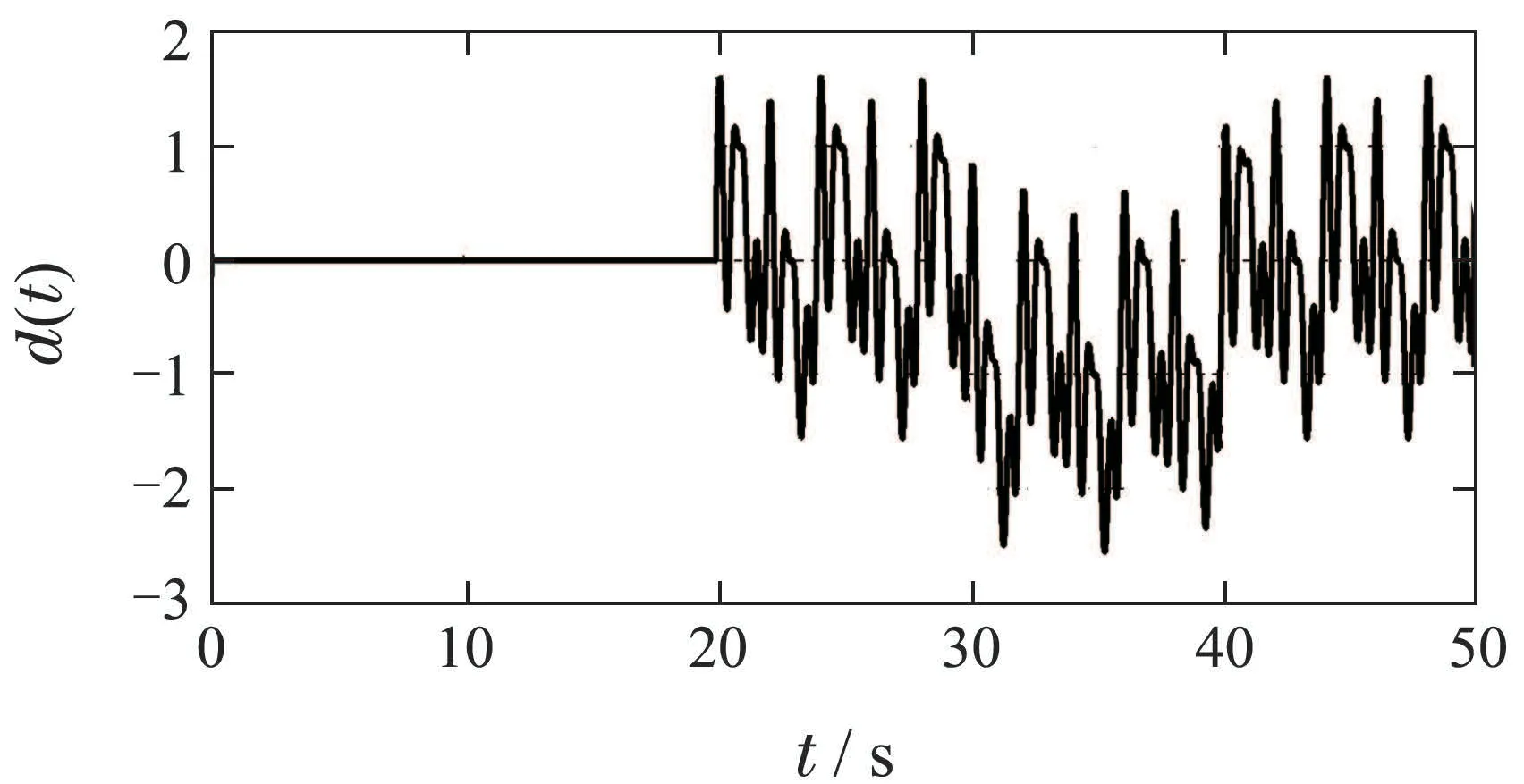
图6 扰动d(t)Fig.6 Disturbance d(t)

在实际应用中,控制输入存在死区不仅会降低系统性能,甚至可能会使得系统不稳定.为了检验系统的抗扰性能,本文对控制输入u(t)存在死区的情形(范围[-0.5,0.5])进行了仿真.如图8所示,系统鲁棒稳定,系统在第3个周期进入稳态,最大稳态跟踪误差为3.2×10−3,很好地抑制了扰动和死区对系统输出的影响.

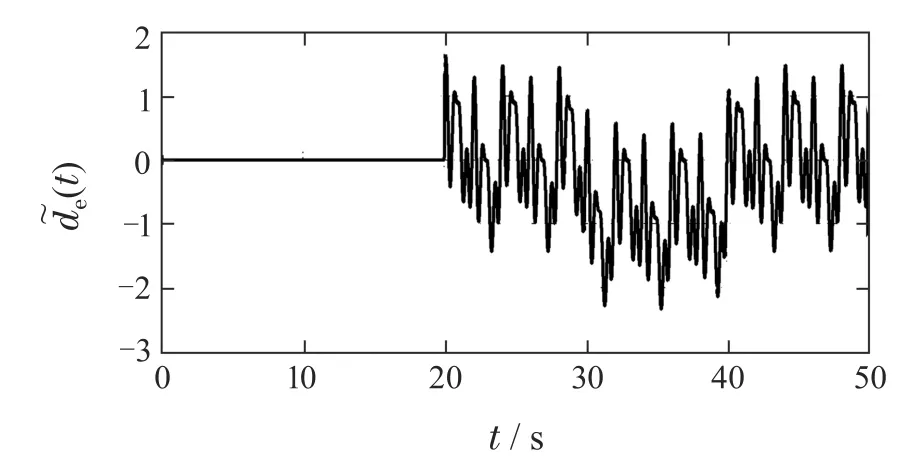
图7 EID估计值˜de(t)Fig.7 EID estimation value ˜de(t)

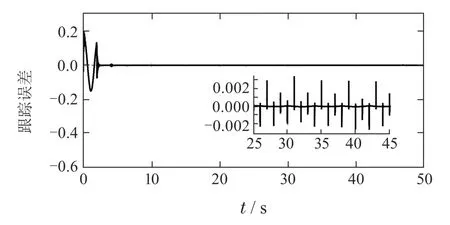
图8 控制输入存在死区的跟踪误差Fig.8 Tracking error with dead-zone in control input

注7PSO作为一种启发式的随机优化算法,在应用到控制系统参数优化时,相同条件下多次寻优得到的参数往往是不相同的,特别是粒子维数较高时这种现象更为明显.本文粒子维数d=9,尽管相同条件下多次寻优结果不完全相同,但其对控制效果影响较小.

4.2 仿真对比分析

图9为在控制器参数相同情况下,基于状态反馈的改进型重复控制(PSO-MRC)方法与本文所提方法系统的跟踪性能及扰动抑制性能对比.由图可知,在没有外部扰动的作用下,两者的跟踪误差是一致的.然而,当系统受到非周期扰动作用时(20 s后),显然,本文所提方法控制系统的扰动抑制能力更强,具体性能指标列于表1,其中ts表示系统从零时刻到第1次进入稳态的调节时间,为过渡过程最大跟踪误差,max|e(t)|t≥20为系统受到非周期扰动后重新回到稳态的过程中最大扰动跟踪误差,ess为最终稳态误差的上界值.

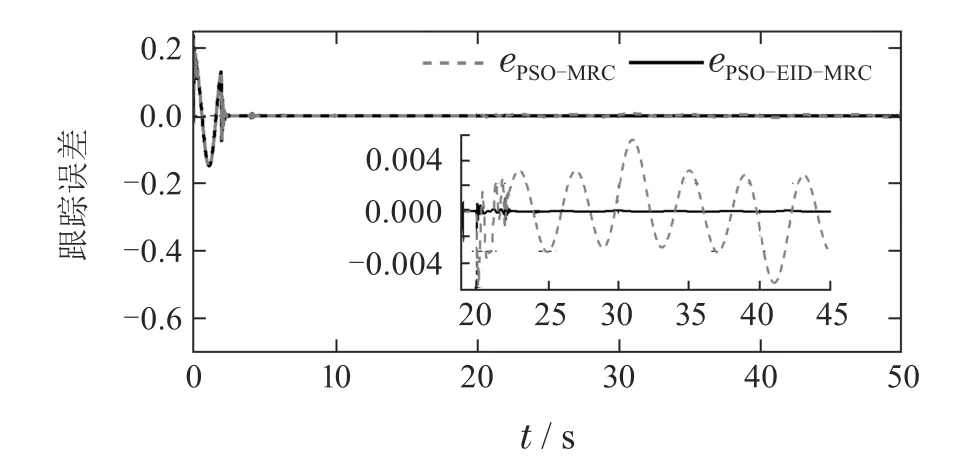
图9 与基于状态反馈的改进型重复控制方法对比Fig.9 Comparing with state feedback MRC-based

为进一步评价本文所提方法的优越性,将本文所提方法与文献[20]中基于EID的改进型重复控制(EID-MRC)方法、基于GESO[27]的改进型重复控制(GESO-MRC)方法做了对比仿真.基于文献[20]中EID-MRC的设计方法,状态观测器极点配置在[-20±100i,-45],具体控制器参数为

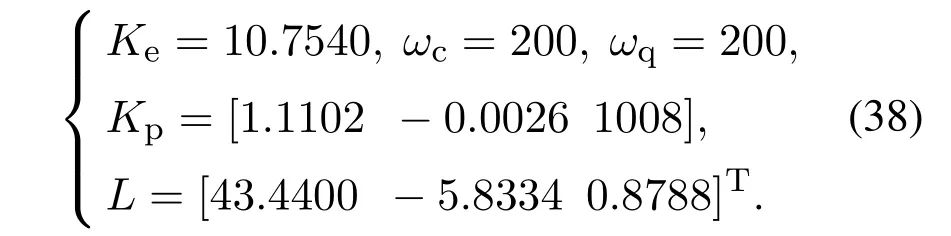
注8PSO-EID-MRC与文献[20]中的EID-MRC除了PSO以外在控制器参数设计方法、稳定性条件和优化性能指标结构等方面不同.后者的低通滤波器参数ωc和ωq预先设定为固定值,具有试凑的痕迹,导致系统的控制性能提高受限,难以取得较好的控制效果.本文ωc和ωq是采用PSO算法进行优化设计,提高了系统设计的灵活性.后者稳定性条件是基于LMI有解的充分条件,具有较大的保守性,且通常较难获得满意的可行解.本文基于小增益定理获得系统稳定性条件,稳定性条件放宽,从而拓宽了EID-MRC方法的应用范围.后者优化性能指标仅仅评价系统的跟踪性能,本文所建立的性能指标函数对系统的稳态性能、暂态性能和扰动抑制性能进行总体评价.

基于GESO的改进型重复控制设计方法,状态观测器极点配置在-4.89±94.24i,状态反馈极点配置在-1.49,具体控制器参数为

由图10和表1可知,无论是暂态、扰动突变还是稳态过程,本文PSO-EID-MRC方法的跟踪性能都优于文献[20]中的EID-MRC方法和GESO-MRC方法.

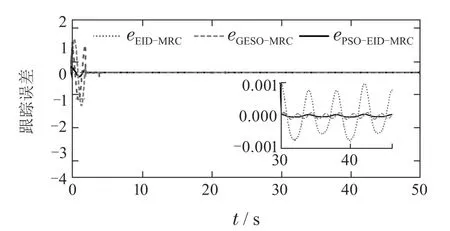
图10 与文献[20]的EID-MRC和GESO-MRC对比Fig.10 Comparing with EID-MRC in the literature [20] and the GESO-MRC

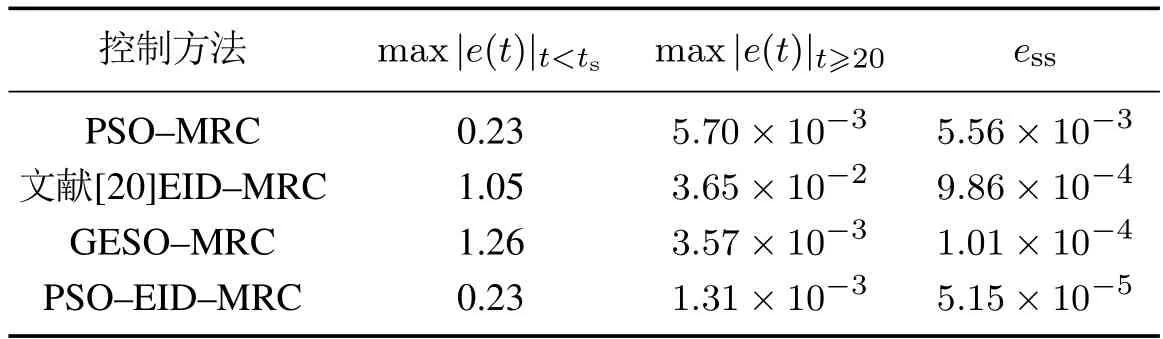
表1 性能指标对比Table 1 Comparison of performance indicators

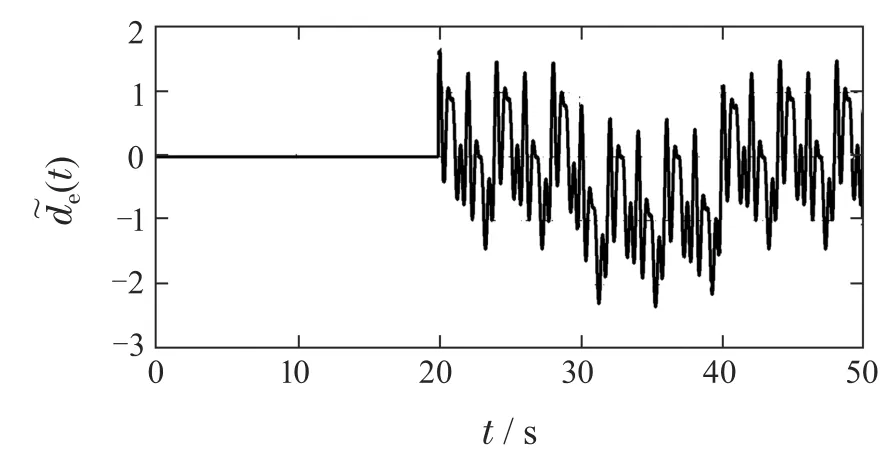
图11 EID-MRC的EID估计值(t)Fig.11 EID estimation value (t)of EID-MRC

图12 GESO-MRC的扰动d(t)及估计(t)Fig.12 Disturbance d(t)and its estimate ˆd(t)of GESO-MRC

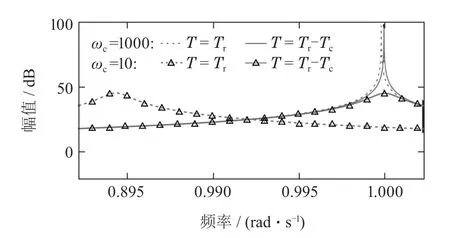
进一步地,为验证重复控制器时滞常数的校正对系统跟踪性能的影响,重复控制器时滞常数分别取为T=Tr和T=Tr-Tc时系统的跟踪误差对比,仿真结果如图13所示,在暂态过程中,两条曲线无明显差别,但是后者的稳态跟踪误差仅为前者的0.0285倍.本文对重复控制器时滞常数的校正显著地提高了系统的稳态跟踪性能.

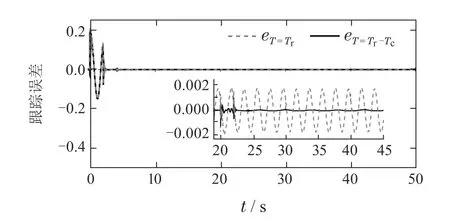
图13 T=Tr和T=Tr −Tc的对比Fig.13 Comparison between T=Tr and T=Tr −Tc

5 结论

针对一类具有非匹配扰动的伺服系统,本文提出了基于EID补偿的重复控制系统参数优化设计方法.基于系统的稳定性条件和综合性能评价指标,建立系统参数的优化模型,实现了对系统重复控制器、EID估计器和反馈控制器参数的同步优化设计,使得系统同时具有满意的非周期扰动抑制性能和周期信号跟踪性能.通过与一般的基于扰动主动补偿的重复控制系统设计方法比较,本文所提方法同时具有更好的扰动抑制性能、过渡过程性能和稳态跟踪性能鲁棒性.本文的创新点主要为如下几点:1)基于重构状态反馈的重复控制规律和EID估计器可以分离设计,提高了系统设计的灵活性;2)建立了一个对系统扰动抑制性能、跟踪性能和过渡过程性能进行整体评价的综合性能指标;3)实现了对重复控制器前馈增益、低通滤波器截止频率、EID估计器参数和反馈控制器参数的同步优化设计,有效地解决重复控制系统中稳定性与稳态跟踪性能、扰动抑制性能和跟踪性能之间的折衷问题.