考虑吸附滞后的页岩气藏流动物质平衡方程

张茂林，张娴，杨龙，张艺钟

1.长江大学石油工程学院，湖北 武汉 430100 2.非常规油气省部共建协同创新中心(长江大学)，湖北 武汉 430100

页岩气直接产于烃源岩中，自生自储、连续成藏[1]。由于储集条件特殊，页岩气以吸附、游离、溶解3种相态存在。长久以来，国内外许多学者基于气体吸附和解吸为物理可逆过程，通过物质平衡法评价页岩气藏储量计算，预测可采储量[2]。KING[3]考虑吸附气推导了一种用于非常规气藏的物质平衡方法；MOGHADAM等[4]提出了一种更广义的适用于所有气藏的物质平衡方程，该方法通过改正气体偏差因子来实现；刘铁成等[5]推导的单组分页岩气藏物质平衡方程考虑了基质体系和裂缝体系；王怀龙等[6]根据双重孔隙介质和吸附相体积建立了页岩物质平衡方程；LOPEZ等[7]发现干酪根中的溶解气也是重要的储气机制，忽略溶解气将导致储量计算的不准确；OROZCO等[8]考虑固态干酪根中的溶解气，建立了物质平衡方程。上述方法虽然相对于KING[3]方法有一定改进，但是均未考虑吸附滞后效应。

另一方面，当地层压力降低时吸附气解吸产生的气体是生产后期的主要产气形式[9]。正如气体吸附用于页岩气藏储量计算，气体解吸对于储层中的气体运移以及生产也至关重要[10]。TAGHAVINEJAD等[11]、YANG等[12]也指出气体吸附和解吸作用在页岩气藏渗流模拟中的重要性。PIERCE等[13]最早提出了解吸过程存在滞后现象，认为与毛细管凝结有关；BELL等[14]研究了几种煤样的吸附(增压)和解吸(减压)等温线发现2个吸附节点不同，从而证实了存在滞后效应；马东民等[15]通过6组煤样的等温吸附-解吸试验发现解吸过程中存在剩余吸附量，提出了降压条件下的解吸拟合方程；张先敏等[16]根据煤层气的吸附滞后效应建立了煤层气藏的物质平衡方程，页岩气与煤层气的相似之处在于页岩气中也存在吸附作用，在页岩气藏开发过程中，页岩气的解吸过程不再遵循吸附曲线，而是遵循等温解吸曲线；DO等[17]通过试验发现等温吸附线不能准确地描述页岩等复杂非均质油藏的吸附-解吸过程；张志英等[18]发现在相同的温压条件下，页岩气的解吸具有滞后现象，解吸不完全；郭为等[19]研究了温度对页岩吸附-解吸的影响，发现页岩吸附曲线与解吸曲线不一致，解吸曲线滞后；通过对比不同的吸附-解吸模型，郭为等[20]还发现解吸式对等温解吸过程拟合效果最佳，证实了页岩气藏存在吸附滞后现象。

而以往的研究在建立物质平衡方程时并未考虑吸附滞后效应，因此物质平衡法会产生一定的计算误差，不能有效指导页岩气藏的开发。此外，页岩气藏由于低孔、低渗，利用物质平衡法计算储量需关井测压，关井时间短，无法直接测量当前平均地层压力；关井时间长，气井生产效果不理想。因此，可在建立物质平衡方程的基础上，进一步使用流动物质平衡法计算储量，避免生产损失。下面，笔者在吸附滞后理论分析的基础上，全面考虑了页岩气藏吸附相体积变化、基质与裂缝体系的储层物性，以及溶解在干酪根中气体的影响，建立了一种新的页岩气藏流动物质平衡方程，为页岩气储层开发动态分析提供了一种更为有效的计算思路。

1 页岩气藏流动物质平衡方程的建立

在建立页岩气藏的流动物质平衡方程时有必要作如下假设：①等温页岩气藏；②以CH4为主要成分，单组分体系；③基质与裂缝体系具有不同的束缚水饱和度；④不考虑水侵，忽略地层水的产生；⑤页岩气藏具有吸附滞后效应。

1.1 吸附-解析式的确定

引用Langmuir吸附等温式[21]计算原始地层条件下的页岩气吸附量：

(1)

式中：VE(pi)为原始地层压力pi下的等温吸附量，m3/t；VL为兰氏体积，m3/t；pi为原始地层压力，MPa；pL为兰氏压力，MPa。

在开发过程中，由于页岩气的解吸遵循等温解吸曲线，因此目前压力下的页岩气吸附量采用马东民等[15]提出的解吸等温式来确定：

(2)

式中：VE(p)为地层压力p下的等温吸附量，m3/t；Vd为最大解吸能力，m3/t；p为地层压力，MPa；pd为等温解吸压力，MPa；Vr为等温剩余吸附量，m3/t。

1.2 页岩气储量计算公式

基质孔隙度:

(3)

式中：φm为基质孔隙度，1；Vpm为基质孔隙体积，m3；Vm为基质总体积，m3。

裂缝孔隙度:

(4)

式中：φf为裂缝孔隙度，1；Vpf为裂缝孔隙体积，m3；V为气藏总体积，m3。

气藏总体积:

V=Vm+Vpf

(5)

原始地层压力下裂缝中游离气体积:

GfBgi=V·φf·(1-sfwc)

(6)

原始地层压力下基质中游离气体积:

GmBgi=Vm·φm·(1-smwc)

(7)

将式(6)变形代入式(4)可得裂缝孔隙体积:

(8)

将式(7)变形与式(8)代入式(5)化简可得裂缝中游离气储量:

(9)

吸附气储量为:

(10)

溶解气储量为:

(11)

式中：Gf为裂缝游离气储量，m3；Bg为地层压力下的气体体积系数，m3/m3；sfwc为裂缝中束缚水饱和度，1；Gm为基质游离气储量，m3；smwc为基质中束缚水饱和度，1；Gasc为吸附气储量，m3；ρb为页岩密度，g/cm3；Gdsc为溶解气储量，m3；cp为甲烷在干酪根本体中的溶解度，m3/m3；TOC为总有机碳含量，%；ρko为干酪根的密度，g/cm3；φads为吸附相孔隙度，1；φorg为游离气孔隙度，1；i为初始值。

1.3 气体的偏差因子Z和综合压缩系数Ct的修正

由KING等[3]推导出的页岩气藏物质平衡方程，进一步考虑吸附滞后及裂缝中的游离气、吸附相体积变化及干酪根中的溶解气修正了偏差因子:

(12)

(13)

(14)

VD=cp·Vdiff

(15)

(16)

(17)

式中：Z**为地层压力下的修正偏差因子，无量纲；Z为偏差因子，无量纲；Gp为累计产气量，m3；G为气藏总储量，m3；psc为标况下压力，MPa；T为气藏温度，K；Zsc为标况下气体的偏差因子，无量纲；Tsc为标况下温度，K；VD(p)为地层压力下干酪根中溶解气体积，m3；ρsc为气体密度，g/cm3；ρs为吸附相密度，g/cm3；Vdiff为气藏总体积中固态干酪根的体积分数，1；b1=-0.018931；b2=-0.85048；b3=827.26；b4=-635.26。

真实气体拟压力:

(18)

式中：μ为气体黏度，mPa·s；m(p)为气藏拟压力，mPa2/(mPa·s)。

式(12)对t求导，可得:

(19)

将式(19)整理为:

(20)

其中:

(21)

式中：qg为日产气量，m3/d。

将式(21)代入式(20)化简得:

(22)

其中:

(23)

将式(23)变换可得:

(24)

将式(24)对p求导可得:

(25)

将式(25)代入式(22)得:

(26)

由式(23)可得:

(27)

对式(27)求导可得:

(28)

将式(2)、式(15)代入式(28)得:

(29)

令:

(30)

其中:

(31)

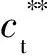
因此:

(32)

1.4 流动物质平衡方程的建立

在拟稳定流动下，引入物质平衡拟时间:

(33)

式中：q(t)为气体流量，m3/d。

对式(32)积分，同时将式(33)代入得:

(34)

由于:

(35)

所以将式(35)代入式(34)，可得:

(36)

又:

(37)

将式(37)代入式(36)，求导可以得到:

(38)

式中：re为气藏边界，m；rw为井径，m；h为气藏有效厚度，m。

在任一半径r处，可将式(38)整理成:

(39)

式中：qr为在半径r处的气体流量，m3。

(40)

由达西公式可得:

(41)

将式(14)、式(18)代入式(41)整理积分得:

(42)

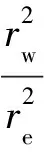
(43)

(44)

式中：m(pr)为气藏在半径r下的拟压力，mPa2/(mPa·s)；m(pwf)为气藏拟井底流动压力，mPa2/(mPa·s)；k为渗透率，mD。

将式(43)代入式(44)，可得:

(45)

将式(45)积分得:

(46)

令:

(47)

则式(46)可整理为:

m(p)=m(pwf)+qb

(48)

由式(48)可将式(36)变形为:

(49)

(50)

则:

(51)

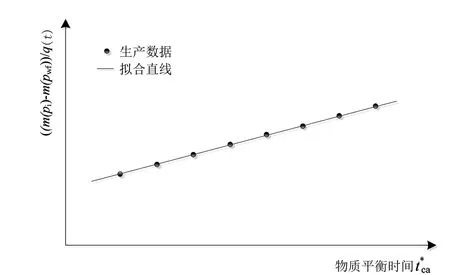
图1 流动物质平衡法储量计算结果示意图

2 实例分析

YE1井储层温度354.07K，压力为43MPa，地层压力系数为1.55。YE1井基本参数如表1所示。YE1井2013年9月23日投产，2013年9月24日按定产6×104m3配产。截至2019年10月3日，井口套压3.42MPa，油压2.78MPa，日产气3.72×104m3左右，根据地面产量，当量年采气速度为1.76%，累计产气5.2611×108m3，采出程度10.37%，井距为600m，水平段长度为1000m。开采时间较长，已经达到拟稳定流动，满足流动物质平衡方程的应用条件，因此选择该井进行计算，YE1井生产动态如图2所示，PVT特性如图3所示，吸附-解吸曲线如图4所示。

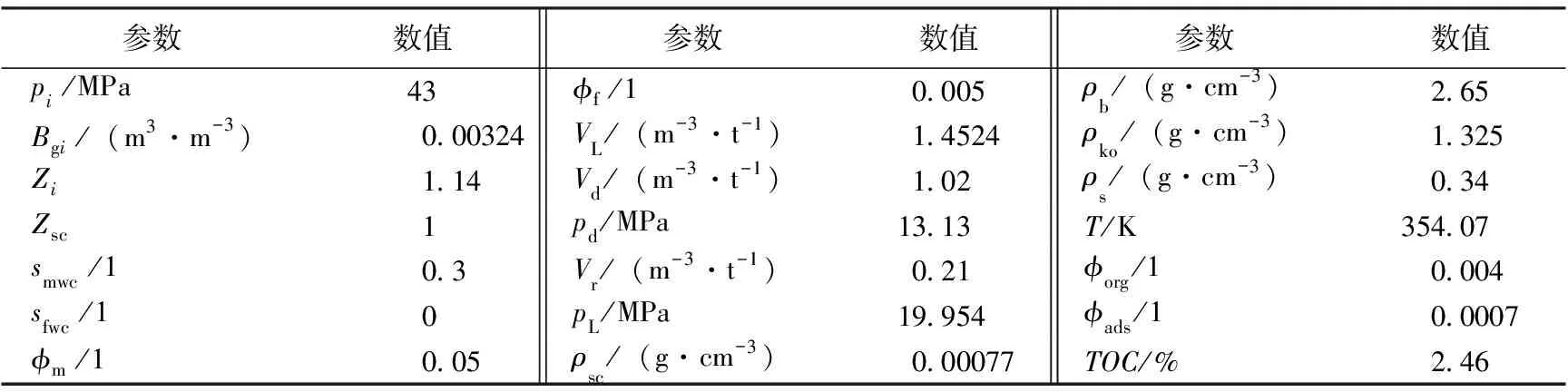
表1 YE1井基本参数

图2 YE1井生产动态曲线图

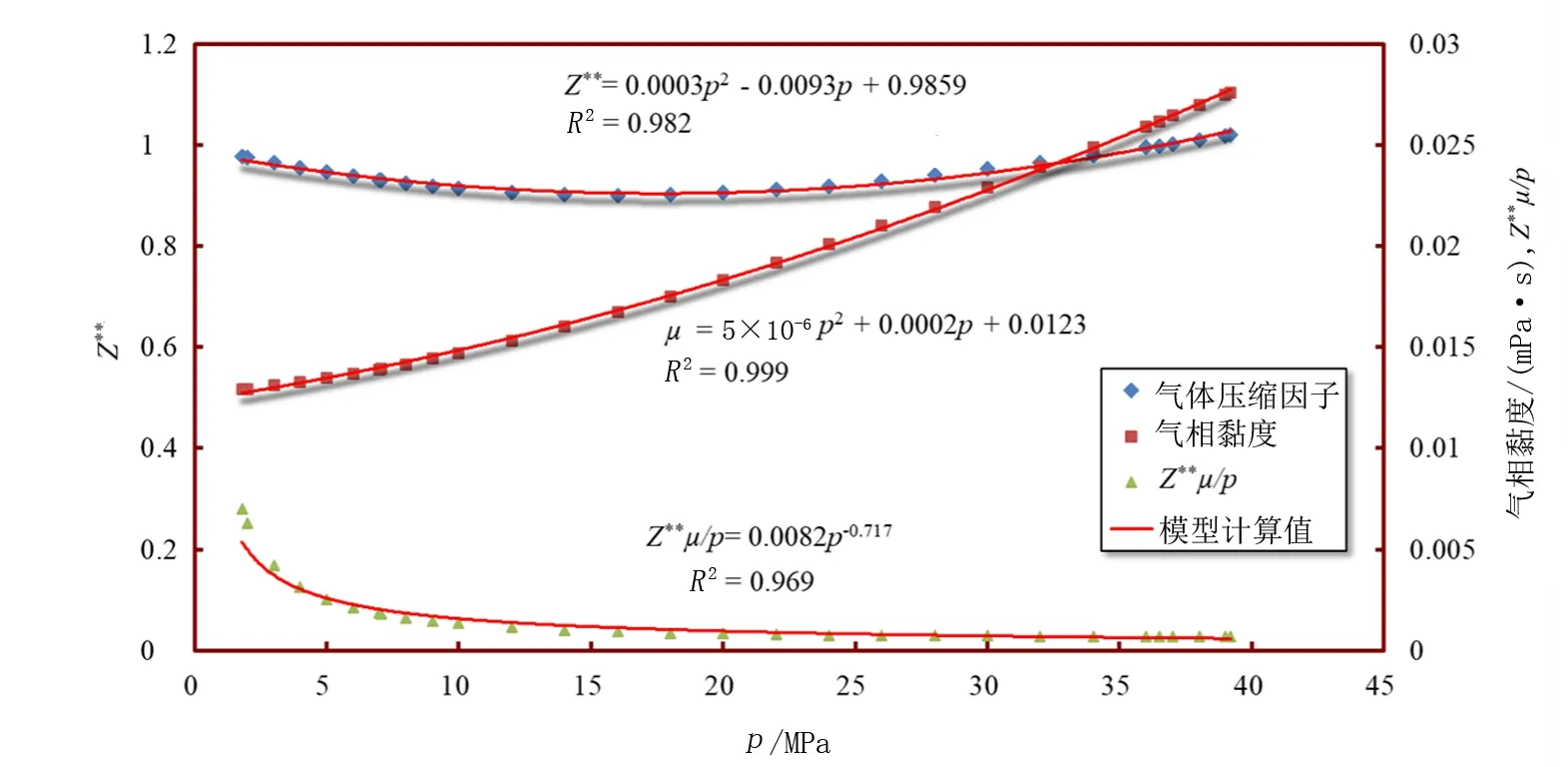
图3 YE1井修正的气体偏差因子、气相黏度、Z**μ/p与压力的相关性

由图4可知，在页岩气藏生产初期，地层压力较高，解吸曲线与吸附曲线基本重合，此时可以忽略解吸效应。随着气藏的继续生产，地层压力开始逐渐降低，解吸效果明显。在页岩气藏开发后期，地层压力降低时采用Langmuir等温吸附参数将低估页岩气藏剩余储量，当地层压力降低到18MPa时，利用吸附参数计算得到的吸附量为0.6888cm3/t，小于利用解吸式计算的吸附量0.8004cm3/t，其相对误差为16.2%，将导致较大的储量误差，造成页岩气藏开发方案的错误制定。

图4 YE1井等温吸附和解吸曲线图(354.07K)

表2 储量计算模型参数

表3 不同方法对应储量

由表3可知，利用传统流动物质平衡法计算出的总储量与实际值的误差达到15.98%，实际值为根据YE1井现场生产数据利用容积法计算的储量值。由于传统流动物质平衡法使用Langmuir等温线计算压力下降时的气体解吸量，未考虑到页岩气解吸具有滞后现象，解吸不完全，影响吸附气剩余储量，进而会影响开发方案的制定，因此，考虑吸附滞后效应非常有意义。其次，传统流动物质平衡法未考虑裂缝中的游离气，在实际生产过程中裂缝中的游离气储量占总储量的8.83%，考虑裂缝中的游离气会使得吸附气储量和溶解气储量占总储量的比例有所下降，对页岩气藏总储量影响较小，说明裂缝在评估页岩气储层储量时不可忽视。按照笔者的方法计算出的各储量值与实际数据相符，证明笔者提出的考虑吸附滞后的页岩气藏流动物质平衡方程的储量评价方法是合理和准确的。

运用考虑吸附滞后建立的流动物质平衡方程进行敏感性分析，计算结果见图5～图7。由图5～图7可知，计算得到的基质中游离气储量随着基质孔隙度的增加而迅速增加，裂缝中游离气量及吸附气量、溶解气量相对减少，且减少幅度保持一致，总储量减少，减少幅度不大；随着裂缝孔隙度增加，裂缝中的游离气量快速增加，基质中游离气量、吸附气量、溶解气量及总储量有所减少；随着吸附相密度的增加，储量计算结果变化不大。因此，基质孔隙度、裂缝孔隙度对页岩气藏动用储量的计算影响较大，吸附相密度的大小对储量计算影响较小。

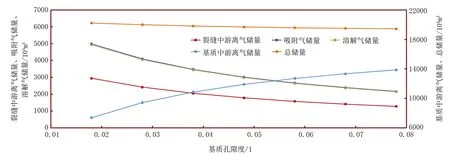
图5 不同基质孔隙度与各储量关系曲线图

图6 不同裂缝孔隙度与各储量关系曲线图

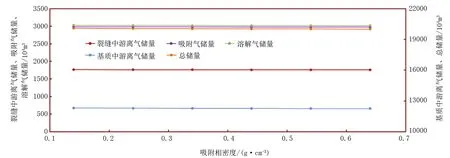
图7 不同吸附相密度与各储量关系曲线图

3 结论

1)页岩气开发应考虑气体解吸效应，忽略页岩气的吸附滞后效应，使用吸附参数计算解吸气量会低估页岩气藏的单井动用储量，实例证明，吸附滞后效应主要影响剩余吸附气储量，对页岩气藏开采后期开发方案的制定有着指导意义。笔者建立的流动物质平衡方程，可以使用井底流压来计算储量，解决了物质平衡法需要关井回压，影响生产的缺点，应用价值更高。

2)物质平衡计算中忽略裂缝中游离气，会导致计算的页岩气储层原始天然气储量偏低。实例表明，裂缝中的游离气约占总储量的8.83%，说明了考虑裂缝中游离气的重要性。

3)基质孔隙度、裂缝孔隙度对页岩气藏动用储量的计算影响较大，吸附相密度的大小对储量计算影响较小。在进行储量计算的时候，需要获取准确的基质孔隙度、裂缝孔隙度。