声学黑洞能量汇聚效应及阻尼耗能机理研究*

鲍岳 刘献栋 梁浩鸣 单颖春 何田

（北京航空航天大学，北京 100191）

主题词：声学黑洞 宽频 功率流 波数域 阻尼

1 前言

振动噪声是影响汽车乘坐舒适性的重要问题之一，目前采用的减振降噪方法往往会造成整车质量增加，开发兼具轻量化和高效减振性能的结构需要新理论的引入。声学黑洞（Acoustic Black Hole，ABH）具有轻量化、便于集成及可设计性强等特性，且可以高效实现能量汇聚，是一种很有前景的被动降噪技术。

声学黑洞效应由Pekeris提出，他发现在非均匀层状流体介质中不存在反射波，其声速随剖面深度的增加而衰减为零。Mironov证明了在厚度呈一定幂指数规律减小的楔形梁中弯曲波将不会发生反射，理论上波速将降低为0。Krylov随后通过几何声学方法推导了声波在这种结构中的程函方程与振幅表达式，并提出了实现声学黑洞效应所需要的条件与结构假设。理论证明，该结构厚度需要降至零才满足声学黑洞效应，但实际上并不存在这种结构，现实中声学黑洞结构都保留一定的残余厚度，而极小的残余厚度都会使得结构中的弯曲波出现大量反射。Krylov 通过在声学黑洞部位贴附少量阻尼，有效减少了弯曲波的反射，实现了声学黑洞结构的能量汇聚效应。

从表可以看出，P值均为0.25，大于显著性水平0.05，卡方对应的P值具有统计显著性，通过显著水平为95%的显著性检验。卡方与自由度之比为1.622，小于2。同时，GFI接近于1，RMSEA小于0.05，以上几个指标均满足模型检验与拟合优度的要求，说明模型拟合效果较好。

常见的声学黑洞包括一维声学黑洞梁结构与二维声学黑洞板结构。目前，声学黑洞的主要研究方法包括传递矩阵法、假设模态法、几何声学法与有限元法。Li等通过传递矩阵法研究了声学黑洞梁的能量汇聚现象，并分析了结构参数对弯曲波能量汇聚的影响。Ma等建立了声学黑洞的半解析动力学模型，分析了阻尼对二维声学黑洞结构的减振效果。Huang等通过几何声学法得出了弯曲波在不同尺寸声学黑洞中的传递轨迹，并研究了弯曲波发生能量汇聚的集中区域，该方法为阻尼的贴附位置提供了参考。Conlon等通过有限元与边界元法研究了声学黑洞阵列结构对薄板振动及声辐射的改善作用，并讨论了通过阻尼布置来优化声学黑洞的减振效果。

本文通过有限元仿真，利用振动功率流法探讨二维声学黑洞中弯曲波的能量分布，并通过波数域方法探究阻尼与黑洞结构的耦合减振机理，对比内嵌单声学黑洞板结构与内嵌黑洞阵列板结构对于能量汇聚、阻尼耗能与结构辐射的不同效果。

2 理论与模型

2.1 声学黑洞理论

为了计算薄板模型的自由场声辐射，在原有薄板模型外层建立声学空腔模型与笛卡尔型理想匹配层（Perfectly Matched Layers，PML），如图2 所示。激励和边界条件与前文相同，空气网格采用四面体单元，网格尺寸为声波最小波长的1/5，同时PML 内部划分8 层以确保吸收外场辐射。最后，采用有限元软件COMSOL计算沿薄板垂直方向距离结构300 mm处的平均辐射声压。

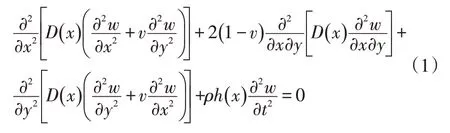
式中，()为抗弯强度；为结构挠度；为材料密度；()为薄板厚度函数；为材料泊松比；为时间变量；、分别为板的横向与纵向尺寸。

2)义棠矿太原组灰岩样品孔隙分形维数与基质孔隙度表现出正相关的关系，而与孔容表现出负相关的关系，分形维数值为2.671 2～2.843 8，介于煤层与砂岩储层之间，与页岩储层分形维数值相近。

根据几何声学假设，板内传播的弯曲波振幅可表示为：

式中，()为弯曲波幅值；()为弯曲波的累计相位，表示为：

式中，为二维均匀薄板的拟纵波波数；()为弯曲波的光程；为弯曲波波数。

设为常数，当薄板结构厚度()呈指数函数变化，即

综上所述，电子胃镜检查是诊断钩虫性十二指肠炎综合征的有效且可靠的诊断方法，做到早发现、早诊断、早治疗。

式中，为与声学黑洞中心点的距离。

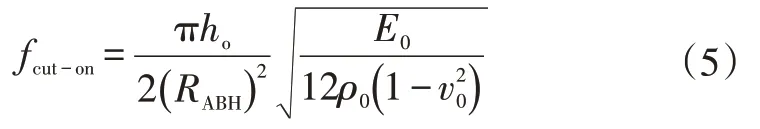
通过有限元模拟计算不同激励频率下薄板各位置的振动速度响应，得到薄板中心正方形区域（200 mm×200 mm）与薄板均匀部分截面的平均振动速度，不同薄板振动位置的平均振动速度对比数据如图3、图4 所示。从图3与图4中可以看出，由于嵌有声学黑洞的薄板刚度较小，中心黑洞区域相比均匀薄板中心区域的振动速度高，贴附阻尼后，当激励频率高于黑洞截止频率时，嵌有声学黑洞薄板的振动速度得到明显改善；板均匀部分处，贴附阻尼的ABH 薄板平均振动速度也低于普通薄板。这说明声学黑洞将板内振动能量汇聚并通过阻尼耗散，并且声学黑洞结构与阻尼的耦合作用明显，但阻尼对平板振动几乎没有改善效果。

2.2 内嵌声学黑洞结构的薄板模型

本文主要研究以下几种薄板结构：均匀平板、背面贴附圆形阻尼的均匀平板、内嵌单声学黑洞结构的平板、背面贴附圆形阻尼的单声学黑洞板、内嵌声学黑洞结构阵列的薄板和背面贴附多个圆形阻尼的声学黑洞结构阵列薄板。所有薄板结构尺寸均为800 mm×800 mm×2 mm，圆形阻尼层的厚度为0.8 mm，半径为30 mm。声学黑洞的厚度函数满足：

且指数≥2时，弯曲波累计相位趋于无穷大，理论上弯曲波无法传播至黑洞边界，这样就形成了弯曲波的能量汇聚效应。但现实中声学黑洞结构都存在一定的残余厚度，同时，声学黑洞的汇聚效应需要满足板内的弯曲波波长小于黑洞直径，故存在声学黑洞效应的下限频率：

不同薄板结构与声学黑洞尺寸如图1所示。

图1 结构模型

薄板模型采用C3D20R二次实体单元建模，为了保证计算精度，每个单元尺寸须小于弯曲波波长的1/10。内嵌声学黑洞钢板与阻尼层采用绑定约束，钢板与阻尼层的材料参数如表1 所示。模型四周边界均采用固支约束。各模型中，使用幅值为1 N的正弦集中力激励薄板的相同位置（见图1），激励频率范围为10～6 000 Hz。使用有限元软件Abaqus对上述模型进行仿真计算。

相关性研究证实,去甲肾上腺素、γ-氨基丁酸及5-羟色胺、谷氨酸等参与了帕金森病痴呆患者疾病的发生及发展,兴奋性神经递质在脑中谷氨酸含量最高,具有生理功能,属于调节剂,可参与脑部智能活动及认知活动,临床研究发现,若能量不足,可导致患者减少谷氨酸摄入量,可增加谷氨酸释放量,升高的谷氨酸可导致患者部分细胞膜发生去极化并导致患者丧失钙离子稳态[3],可增加NMDA受体内流并产生背景噪音,可对突触信号检测造成影响,若钙离子水平持续增加可导致患者出现神经变性,可诱导患者下降认知功能,可表现出退行性痴呆临床症状[4]。

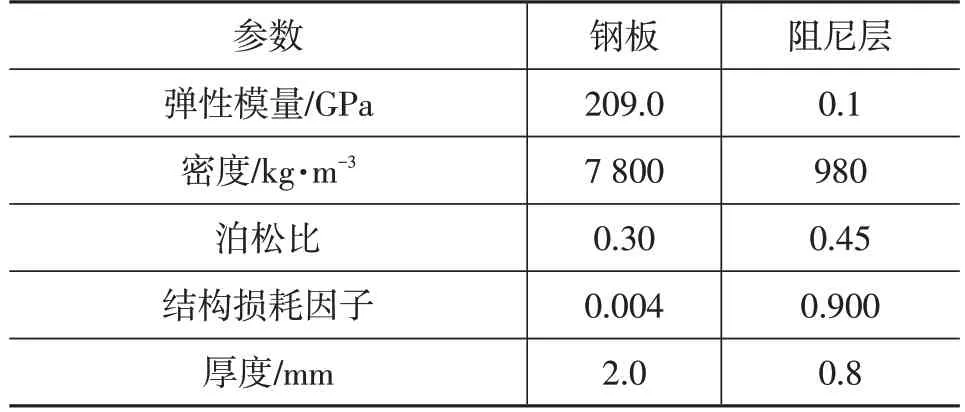
表1 钢板与阻尼的材料参数

对于变厚度薄板结构，弯曲波波动方程为：

②州城即山阴县城，秦始皇改大越为山阴县，属会稽郡。南朝宋在会稽郡置东扬州，齐、梁、陈因裘，州治设在山阴县城，故山阴城也称州城。

图2 板-声腔耦合模型

3 振动功率流与波数域分析

3.1 振动功率流分析

声学黑洞对稳态振动下的弯曲波能量汇聚作用明显，在瞬态激励下也能观察到相似现象。对瞬态激励下声学黑洞模型进行时域分析，施加1 000 Hz正弦信号激励，载荷时长为7 ms，所有时间段内声学黑洞区域的时域平均振动速度如图10所示。由图10可以看出，贴附阻尼后声学黑洞的振动速度明显降低。3 个截面处声学黑洞薄板不同区域振动速度与时间的关系如图11所示，与前文频域分析结果一致，弯曲波能量最大的区域位于声学黑洞中央区域，但并非圆心位置，而是略微偏离中心，与激励方向的位置相反。可以看出，声学黑洞对于声波的汇聚与“凸透镜”对于光波的汇聚作用非常相似。

水是生命之源、生态之基。习近平主席指出“绿水青山就是金山银山”。当前水资源面临资源短缺，地下水储量不足，导致地表水逐渐成为饮用水水源。因地表水易受污染，水源保护尤其重要。要大力保障饮水安全、供水安全、生态安全，着力解决人民群众最关心、最直接、最现实的水资源问题。

通过傅里叶变换可以得到对应频域的复功率流()的表达式：

（1）强调团队协作，营造和谐氛围，保证职责分明而不影响亲和力，确保全体员工均能全身心投入。首先，应形成良好的合作意识，保证日常住宿与饮食，并提高自身责任心，同时，在不影响日常工作的基础上，丰富业余生活，以此进一步提高凝聚力。

式中，()为结构上某一点外力的傅里叶变换结果；()为该点速度傅里叶变换结果的共轭复数。

复功率流包括有功功率与无功功率。在简谐激励条件下，有功功率流等于时间平均功率流，表示单位周期内的平均能量。

3.2 波数域分析

时间域可以通过一维傅里叶变换变换到频率域，同样地，空间域的振动能量分布也可以通过二维傅里叶变换变换到波数域。本文采用振动速度来描述薄板的振动能量，变换公式为：

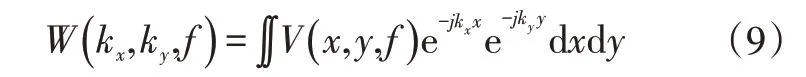
式中，k=2πξ、k=2πξ分别为、方向的波数，ξ、ξ分别为、方向的空间频率；(k,k,f)为经过二维傅里叶变换后波数域上的频谱幅值；()为在频率处的振动速度幅值。

波数域分析能够清晰反映弯曲波在传播过程中波长的变化情况，有助于揭示声学黑洞结构的能量汇聚机理及阻尼耦合效应。

式中，()、()分别为结构上某一点的瞬时外力与瞬时速度；为观测时长。

4 数值计算结果

4.1 内嵌单声学黑洞薄板的能量汇聚效应分析

式中，为声学黑洞的半径；为薄板均匀部分厚度；为材料的弹性模量；为材料密度；为材料的泊松比。

轮对存放库体型大，整体运输较为困难，因此，采用分步制造的方式。制造加工时在制造厂进行焊接、加工和组装后，分段运输到现场进行安装。立柱与地面采用地脚螺栓进行联接固定，整个轮对存放库安装完毕后，进行外观处理。

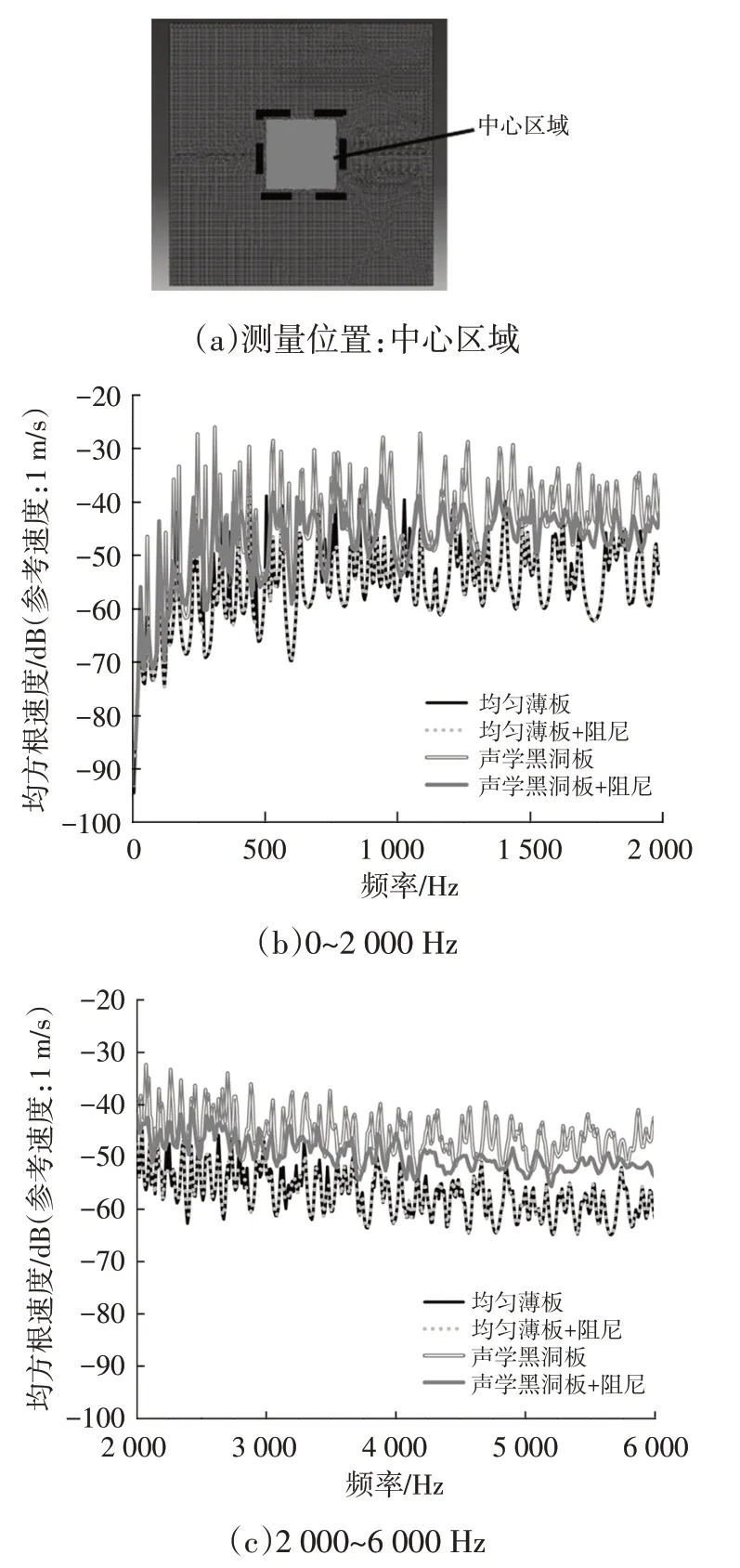
图3 不同薄板结构中心区域的均方根振动速度对比

图4 不同薄板结构均匀厚度区域的均方根振动速度对比

进一步计算黑洞区域中弯曲波能量功率流分布情况，图5 所示为施加激励频率分别为200 Hz、2 000 Hz、6 000 Hz 下黑洞区域的二维功率流云图。由图5 可以看出：在截止频率以上，在声学黑洞区域附近功率流矢量发生偏转，汇聚于黑洞中心的残余厚度区域附近，且位于声学黑洞中心区域的功率流能量远大于黑洞区域外，而低于截止频率的弯曲波能量不发生汇聚。

图5 不同激励频率下声学黑洞区域的二维功率流云图

为了更加直观地表示弯曲波在薄板中的能量分布，将每个频率下的功率流能量进行平均，不同薄板在全频段功率流的平均能量如图6所示，贴附阻尼的声学黑洞结构在低频、中频和高频段的能量耗散作用对比结果如图7 所示。从图中可以看出：在截止频率以上，声学黑洞能量汇聚效应明显，贴附阻尼后弯曲波能量明显衰减；在截止频率范围以下，振动能量并未出现降低。上述结果说明，只有当激励频率高于截止频率时，声学黑洞才会发生显著的能量汇聚及阻尼耦合效应。由此可知：均匀薄板不发生能量汇聚，贴附阻尼层对板内弯曲波能量耗散作用十分有限。

图6 全频段（0～6 000 Hz）平板与声学黑洞结构贴附和不贴附阻尼的平均功率流图对比

图7 低、中、高频激励下声学黑洞与声学黑洞结构贴附阻尼的平均功率流图对比

将仿真得到的板内振动速度空间分布情况通过二维傅里叶变换得到弯曲波在板内传播的波数域分布。图8 所示为全频段内3 种薄板的波数域能量分布情况，低、中、高频激励下的波数域图像对比结果如图9 所示。可以看出：施加的载荷频率越高，薄板内的弯曲波振动波长越短，波数增加；针对高于截止频率的激励频率，相比均匀薄板，内嵌单ABH 薄板的弯曲波波数分布出现低波数向高波数的迁移现象，弯曲波波长压缩现象明显；贴附阻尼后，图像中外围的高波数能量降低。

图8 全频段（0～6 000 Hz）平板与声学黑洞结构贴附和不贴附阻尼的平均振动速度波数对比

图9 低、中、高频激励下平板与声学黑洞结构的平均振动速度波数对比

振动功率流分析是一种直观描述结构在单位面积截面上的能量强度与传递方向的方法。时间平均功率流()的表达式为：

图10 7 ms内声学黑洞结构贴附和不贴附阻尼的时域平均振动速度分布

图11 内嵌声学黑洞结构不同截面处的平均振动速度曲线

4.2 声学黑洞阵列的能量汇聚效应分析

为了进一步考察薄板内嵌黑洞阵列结构的振动性能，通过仿真计算了内嵌声学黑洞阵列薄板振动速度，该声学黑洞阵列结构含有5 个声学黑洞单元。同时与之前讨论的单个声学黑洞结构进行对比，不同结构的振动速度如图12 与图13 所示。其中内嵌ABH 阵列板与内嵌单个ABH 薄板振动速度都高于平板，但阵列板振动速度低于单ABH 板，这是由于多个声学黑洞分散了板内的振动能量。相比单声学黑洞，声学黑洞阵列与阻尼的耦合效应更加明显；当施加载荷激励低于声学黑洞的截止频率，即在300～500 Hz 范围内时，贴合阻尼后ABH 阵列板的振动水平有了明显改善，这与内嵌单声学黑洞板的现象不同。

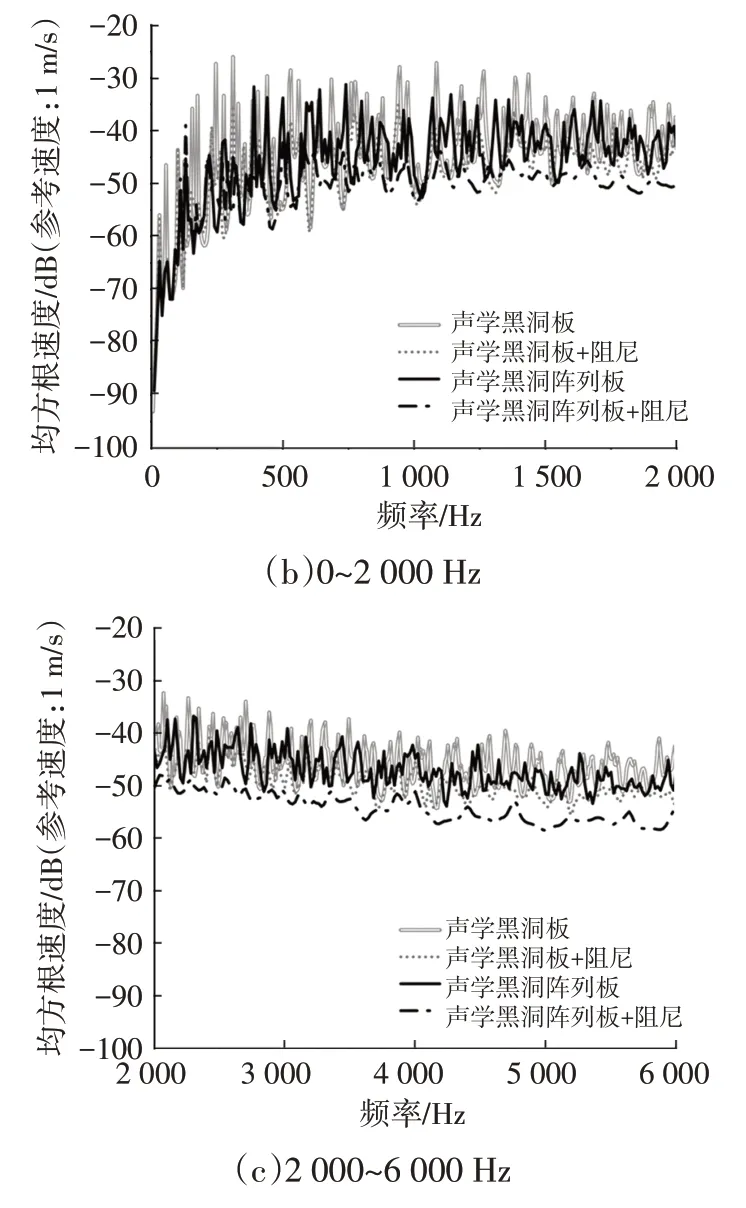
图12 不同薄板结构中心区域的均方根振动速度对比

图13 不同薄板结构均匀厚度区域的均方根振动速度对比

声学黑洞阵列板的平均功率流能量如图14 所示，相比内嵌单个黑洞，声学黑洞阵列板结构对振动衰减作用更加明显。不同频率段的平均功率流分布如图15所示，声学黑洞阵列对于截止频率内的低频激励仍然存在很强的能量汇聚与阻尼耦合效应。

图14 全频段（0～6 000 Hz）声学黑洞与声学黑洞阵列结构贴附和不贴附阻尼的平均功率流

图15 低、中、高频激励下声学黑洞阵列与声学黑洞阵列贴附阻尼结构的平均功率流

声学黑洞阵列板的波数域图像如图16 所示，声学黑洞阵列对高波数能量的衰减作用明显强于单声学黑洞薄板。各频率段振动波数域图如图17 所示，低于截止频率500 Hz 时，阻尼对声学黑洞阵列板振动能量的减弱效果就已经非常明显；同时，由于多声学黑洞结构分散了板内的低波数能量，使得低波数域能量也出现了明显降低。由此证明，相比于内嵌单个黑洞薄板，声学黑洞阵列不仅对于全频段振动能量衰减具有更优效果，同时也能改善因为声学黑洞截止频率存在而导致单个声学黑洞低频减振效果较差的问题。

式中，l为光伏方阵的斜面长度；θ为光伏方阵的安装倾斜角度；h为障碍物的高度；β为太阳方位角，均为正值；α为太阳高度角。若建筑中存在方位偏角σ，则需要将公式中的β替换为β+σ进行分别计算，以二者之间的较大值作为方阵间距值。而针对坡屋面1的类型，处于屋面南坡的光伏间距D1因为受到屋面坡度角的影响会导致间距相对较小，屋面北坡的光伏间距D2则会变大，光伏方阵的间距计算图如图2所示。

图16 全频段（0～6 000 Hz）声学黑洞与声学黑洞阵列结构贴附和不贴附阻尼的平均振动速度波数

图17 低、中、高频激励下声学黑洞阵列与声学黑洞阵列贴附阻尼结构的平均振动速度波数

4.3 声学黑洞与阻尼耦合机理分析

通过复模态计算可以得到整体系统的模态阻尼损耗因子，清楚地表征薄板结构与阻尼之间的耦合作用。3 种不同薄板结构的模态阻尼损耗因子与频率的关系如图17 所示。当激励频率高于截止频率时，板内的弯曲波波长小于黑洞尺寸，弯曲波整体进入黑洞结构，振幅变大，波长被压缩，此时薄板整体结构与阻尼发生相互作用，在相当宽的频域内阻尼损耗因子显著提升；而当激励频率低于截止频率时，弯曲波波长大于声学黑洞尺寸，此时黑洞结构不再具有能量汇聚效应，但黑洞结构的局部模态与阻尼层之间仍存在强烈的耦合作用，这也可以改善整体结构的模态阻尼。但是，这种阻尼耦合效应只在局部模态频率下才起作用（图18 所示为内嵌单声学黑洞与阻尼耦合的前3 阶模态振型），因为单个黑洞结构在低频的局部模态数量少，所以阻尼对内嵌单声学黑洞板的低频振动改善效果有限。而多声学黑洞阵列的结构具有复杂性，使得黑洞阵列结构在低频下也具有相当丰富的局部模态数（不同板结构的模态数量与频率的关系如图19所示），这一特点诠释了声学黑洞阵列板在低频范围内也具有很好的减振效果的原因。

图18 不同板结构各模态频率下的模态损失因子及声学黑洞结构的前4阶局部模态振型

图19 不同板结构模态数量与模态频率的关系

同时，由于板内弯曲波波长被压缩，薄板振动表面与声场的耦合匹配特性变差，使得薄板的声辐射降低。不同板结构的辐射声压幅值与频率的关系如图20 所示，由图20可以看出，声学黑洞阵列与阻尼的耦合效应能显著改善薄板的自由场辐射声压，相比普通平板结构，声学黑洞阵列辐射声压最大可降低10 dB。

大电网中虚拟同步发电机惯量支撑与一次调频功能定位辨析//秦晓辉,苏丽宁,迟永宁,郭强,徐希望//(9):36

图20 3种板结构的自由场辐射声压值对比

5 试验验证

为进一步验证声学黑洞的效果，本文加工了声学黑洞薄板结构，并搭建了试验平台进行振动测试，如图21 所示。按照前文的仿真模型，将带有单个声学黑洞的平板结构通过铝型材固定。尽管实际条件与仿真模型存在些许差异，但不会影响相应的物理现象。同时，引入了阻尼结构来验证声学黑洞薄板与阻尼材料的耦合效果。

图21 试验装置

试验中，信号发生器产生一个频率为1 000 Hz 的激励信号，并通过功率放大器驱动电磁激振器激励薄板，激励点位置坐标为(670 mm,300 mm,2 mm)。采用加速度传感器采集振动信号，激励位置与测量位置分别如图22 所示，测试原理如图23 所示。谐波稳定后，对每个点信号进行采样，采样时间为5 s。该测试过程采用了重复性验证方法，排除了偶发因素对结果精度的影响。

图22 激励与测量位置

图23 测试原理

将所采集的信号通过平均可得到声学黑洞区域的振动加速度，如表2所示。通过对比带有阻尼的ABH平板结构，可以看出：该方法大幅降低了振动能量，声学黑洞与阻尼的耦合效果非常明显。

将建立的三维模型导入comsol软件中，进行网格划分，由下图可以看出，网格划分较好，进行有限元计算可以得到较为精确的结果；输入材料的基本参数及设定的外界条件，以天（d）作为计算单位，混凝土温度测试时间为20d，步长为3d，利用comsol软件，对在筏板基础中选取的测点进行模拟计算，与实测数据进行对比分析。

表2 振动加速度测量值

6 结束语

本文应用有限元方法研究了3 种类型薄板（均匀平板、内嵌单个声学黑洞薄板与内嵌声学黑洞阵列薄板）的弯曲波能量汇聚效应及振动响应。通过振动功率流与波数域方法研究了弯曲波在声学黑洞结构中的汇聚现象与波数变化情况，并对低频及中高频激励下的声学黑洞阻尼耦合机理进行了探究。通过对比这几种板结构的减振效果及声辐射大小，证实了贴附阻尼的声学黑洞结构可以有效改善薄板全频段的振动与辐射特性。