自动驾驶汽车状态估计的矩阵加权自适应扩展卡尔曼滤波方法

初宏伟 张颖

（1.长春汽车工业高等专科学校，长春 130013；2.一汽-大众汽车有限公司，长春 130013）

主题词：自动驾驶汽车 多传感器 状态估计 执行机构故障 卡尔曼滤波

1 前言

自动驾驶感知系统的性能多依赖于其所配置的传感器硬件方案及相应的汽车状态估计方法。现有自动驾驶汽车所配置的传感器包括惯性导航系统（Inertial Navigation System，INS）、全球定位系统（Global Positioning System，GPS）、雷达、光学传感器等。

以轮胎侧向力传感器为数据源，文献[5]、文献[6]采用递归最小二乘方法估计侧向车速，但因对环境噪声存在高斯噪声假设，其跟踪存在一定时延。文献[7]通过车速传感器的信号，采用龙伯格（Luenberger）观测器法实现了道路坡度的估计。文献[8]采用扩展卡尔曼滤波器实现了车轮侧偏角的估计，但噪声信息未知导致其状态估计存在一定偏差。文献[9]采用无迹卡尔曼滤波器实现了汽车速度估计，并在BMW5上进行了实车试验，纵、侧向速度跟踪较好。

单一传感器量测的可靠性相对较差，而采用不同传感器能够实现信息融合，从而获得更为精准的目标信息。目前，欧盟已开始研究雷达与光学传感器的融合技术。在国内，潘璞利用全球导航卫星系统（Global Navigation Satellite System，GNSS）/INS 组合导航系统设计了自适应卡尔曼滤波方法实现自动驾驶汽车的姿态解算。沈峥楠融合超声波雷达和可见光摄像头实现了车位几何信息识别。彭文正等采用迭代扩展卡尔曼滤波算法融合了惯性测量单元（Inertial Measurement Unit，IMU）、GPS、相机等信息，实现了车辆的定位和速度观测。刘志在深度学习框架下实现了多源信息的深度融合。综上所述，多传感器信息融合技术已然成为当前自动驾驶汽车状态估计领域的研究热点。

现有方法鲜有讨论汽车故障条件下的状态和故障联合估计问题。为此，本文针对自动驾驶汽车提出了一种多传感器加权融合自适应扩展卡尔曼滤波（Adaptive Extended Kalman Filtering，AEKF）状态估计方法，通过设计矩阵加权融合方法实现多传感器信息融合，从而提升感知系统量测精度，以期为自动驾驶汽车的自动泊车、自动避障等应用场景提供参考。

2 自动驾驶汽车运动学模型

自动驾驶汽车运动学模型如图1所示。根据汽车运动学规律，将上述关系在惯性系下建模为以下运动学方程：

图1 自动驾驶汽车运动学模型

式中，()为汽车质心在惯性系下的坐标；为车速；为汽车加速度；为汽车行驶航向角；、分别为车辆质心与前、后轴的距离；为汽车行驶方向与车身纵轴的夹角；为汽车前轮转角。

为便于数字化工程设计，在假设转向角很小的情况下（≈），将式（1）转换为离散形式：

式中，、、、、、、分别为系统时刻、、、、、、的采样值；Δ为数字测控系统的采样时间。

本文的目标是针对离散系统式（2），设计多传感器矩阵加权融合AEKF 估计器，以降低整车成本、提升测控系统的量测精度，实现自动驾驶汽车行驶状态和执行机构故障的同步估计。

3 汽车行驶状态估计方法

3.1 自适应扩展卡尔曼滤波

为便于自适应扩展卡尔曼滤波器设计，同时考虑执行机构故障情形，将离散系统式（2）转化为常规系统描述形式：

非线性动态方程(x,y)∈R的表达式为：

由于转换后的系统式（3）存在非线性方程式（4），故采用扩展卡尔曼滤波器设计思路对其进行线性化处理。线性化后的系统为：

至此即完成了系统模型的转换。本文自适应扩展卡尔曼滤波器设计如下：

a.给定迭代估计的初始条件：

式中，、为系统状态量初始值；()0、为执行机构故障参数初始值；、为协方差矩阵的初始值；(0)、(0)均为用于求解最优增益矩阵K的辅助矩阵。

b.协方差矩阵一步预测：

c.状态估计增益矩阵更新：

式中，Σ=CP+R；R为当前时刻噪声方差矩阵。

d.故障估计增益矩阵Γ更新：

e.式（9）中对应辅助矩阵H、S、Ω、Λ更新：

式中，为待设计遗忘因子。

通过式（6）～式（13）的迭代计算，即可通过单个传感器信息估计得到自动驾驶汽车的状态和故障信息。关于自适应扩展卡尔曼滤波收敛特性的探讨参见文献[17]。

3.2 多传感器矩阵加权融合估计方法设计

为解决单一传感器高精度测控与高成本的矛盾，有效提高自动驾驶汽车整车制造的费效比，通过配置制造成本较低的传感器，并利用传感器信息融合技术对汽车状态进行在线估计成为了工业界的热点研究方向之一。

设传感器数量为，通过各传感器的信号滤波得到的无偏估计x：

式中，表示数学期望。

式中，M∈R为加权矩阵。

在线性最小方差意义下，选择M来极小化估计误差分量均方和：

式（16）等价于：

式中，为加权估计的协方差矩阵；()为矩阵的迹。

因局部估计和融合估计均具有无偏性，则以下约束条件成立：

根据式（18）可知：

为了求取各加权矩阵M，设加权矩阵的合成阵为：

定义未知方差矩阵合成矩阵为：

根据上述定义，性能指标式（17）可写为：

而约束条件式（18）可转换为：

至此，求解矩阵的问题转换为以式（22）为性能指标的矩阵等式约束极小化问题。采用拉格朗日乘数法，引入辅助函数：

式中，γ=[γ… γ]为拉格朗日乘子向量；e=(0,…,0,1,0,…,0)，其第列元素为1，其他为0。

为极小化性能指标式（24），对辅助函数求的偏导数并令其等于0，即∂/∂=0，可得：

上式第2项可以写成如下形式：

式中，=(,…,γ)=(γ)，该矩阵的第行第列为γ。

根据式（25）和式（26），可得：

辅助函数对求偏导并令其等于0，即∂/∂=0，则有：

根据上述推导可知：

求解线性方程组式（29），可得：

由式（30）可推知=I，进而可知：

推知：

上述推导存在如下关系：

根据协方差矩阵定义可知：

综合上述推导过程，得到多传感器矩阵加权融合估计：

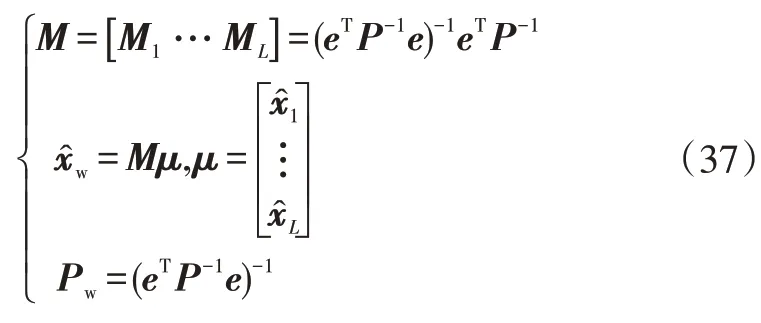
本文所设计方法的整体应用框架如图2所示。

图2 本文方法框架

4 仿真分析

4.1 仿真条件设置

为验证本文所提出的方法的有效性，将本文所提出的AEFK（矩阵加权）方法与单个传感器的AEKF方法进行对比。验证方案中，采用了2种不同精度的传感器对汽车状态信息进行感知，并设置如表1所示的仿真参数进行方法验证。

表1 仿真参数

4.2 仿真结果及分析

利用表1 中所设计的仿真参数，以MATLAB 2018b为仿真平台搭建仿真模型，设置了3种仿真情形：

a.采用低精度传感器1（=0.8）进行状态信息采集，并利用3.1 节的AEKF 方法进行状态和故障系数估计，记为AEKF（传感器1）；

b.采用高精度传感器2（=0.2）进行状态信息采集，并利用3.1 节的AEKF 方法进行状态和故障系数估计，记为AEKF（传感器2）；

c.基于情形a 和情形b 得到的估计结果，利用3.2节的多传感器矩阵加权融合方法进行状态和故障估计，记为AEKF（矩阵加权）。

根据上述仿真情形和表1的仿真参数设置，得到仿真结果如图3～图7所示。

图3 汽车位置估计结果

图4 汽车行驶航向角估计结果

图5 汽车速度估计结果

图6 故障系数估计结果

图7 方差矩阵的迹

由图3 可知，高精度传感器（传感器2）能够得到更好的估计结果。虽然3 种情形均能保证汽车行驶位置的有效跟踪，但本文所提出方法的融合估计结果显然优于单个传感器的估计结果，精度更高。

由图4、图5 可知，本文所提出的方法能够有效、较好地实现汽车行驶航向角的高精度估计。结合图3～图5 可知，本文方法能够实现自动驾驶汽车位置、航向角和速度的高效估计。

由图6可知，本文方法还具备执行机构故障的估计能力，且较单个传感器估计情形具有一定优势。综合图3～图6可知，本文方法不仅能够保证自动驾驶汽车在正常状态下的状态感知，还可实现故障情形下执行机构故障系数的有效估计，保证了自动驾驶汽车行车全过程的安全、可靠。

由图7可知，所提出方法的方差矩阵的迹随着时间推移收敛更快，意味着参数收敛更快。这也是该方法估计结果快速高效的内在原因。

为进一步量化对比所提出方法的优势，以故障估计误差的统计学均方误差（Mean Squared Error，MSE）和误差标准差（STandard Deviation，STD）为量化指标，将本文方法与对比方法（单个传感器）统计学信息进行对比，如表2所示。

表2 仿真结果统计学分析

对比表2 中的均方误差结果可知，矩阵加权AEKF方法的误差均值最小，则状态估计效果最佳。进一步对比误差标准差结果可知，矩阵加权AEKF的跟踪误差标准差最小，说明所提出的估计方法与汽车实际状态的偏差较小，能够保证误差估计的快速、平顺，从而保证自动驾驶汽车控制系统的稳定运行和行车安全。

5 结束语

针对自动驾驶汽车状态和故障估计问题，本文在自适应扩展卡尔曼滤波理论基础上提出了一种矩阵加权多传感器信息融合估计方法。仿真验证结果表明，较之单个传感器的状态和故障估计方法，所提出的方法能够较好地实现汽车行驶位置、航向角、速度以及执行机构故障的高效估计，为汽车自动避障、自动泊车等提供一定技术参考。

本文方法虽能实现汽车状态和故障的有效估计，但由于EKF方法需已知外部扰动和传感器量测的噪声统计特性，实际应用中较难准确获取上述信息，下一步工作将致力于噪声特性的在线建模，同时尝试将工程应用中的不同真实传感器数据源引入本文算法进行实测数据验证，以期得到工程实用性更强的自动驾驶汽车状态融合估计方法。