浅析思维导图在高中数学教学中的应用
张丙亮
思维导图具有架构简单、实用性强的特点.高中数学知识比较抽象,且知识点较多,因而在高中数学教学中,运用思维导图辅助教学,不仅能帮助学生快速构建知识网络,还能使其明确知识之间的联系,有效提升学习的效率.
一、思维导图在新授课教学中的应用
在新授课上,为了帮助学生很好地理解新知识,教师可利用思维导图来建立新旧知识之间的联系,使学生明白各个定义、公式、性质等是如何得到的,其应用条件和适用范围等.
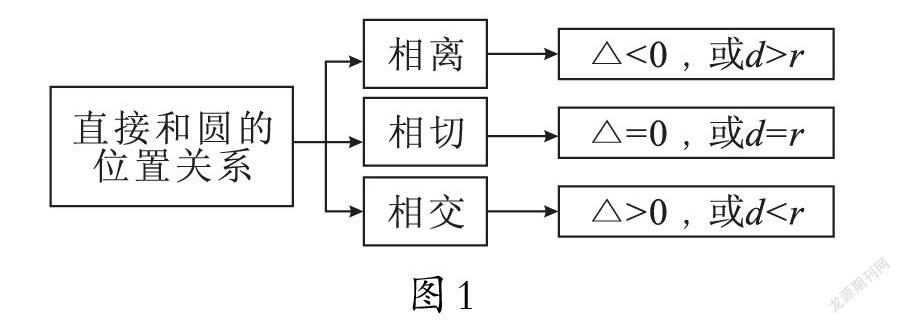
例如,在讲解《直线与圆的位置关系》时,笔者首先引导学生回顾了初中所学的直线与圆的知识,问道:“直线与圆的位置关系有哪几种?”学生通过回忆很快回答到:“相离、相切、相交.”然后笔者逐步绘制出如图1所示的部分思维导图.接着问道:“那么如何判定直线与圆的这三位置关系呢?”有的学生表示:“可以观察图形中直线与圆的位置.”有的学生表示:“可以比较圆的半径 r 和直线与圆之间距离 d 的大小.”接着笔者说道:“我们已经学习了圆的方程、直线的方程,那么能不能根据它们的方程来进行判断呢?”很快学生想到了,将直线与圆的方程联立,构造一元二次方程,通过讨论方程的根的判别式来确定直线与圆的位置关系,即:当△<0时,直线与圆相离;当△=0时,直线与圆相切;当△>0时,直线与圆相交.最后得到了如图1所示的完整的思维导图,这样学生便能将直线与圆的三种位置关系跟方程的判别式、直线与圆的距离、圆的半径关联起来,形成完成的知识体系,也掌握了两种判断直线与圆位置关系的方法.
二、思维导图在复习课中的应用
在复习课中,运用思维导图将抽象定理、概念、性质、方法等关联起来,以直观的形式呈现出来,不仅能帮助学生建立完整的知识体系,明确知识之间的联系,还能强化记忆.
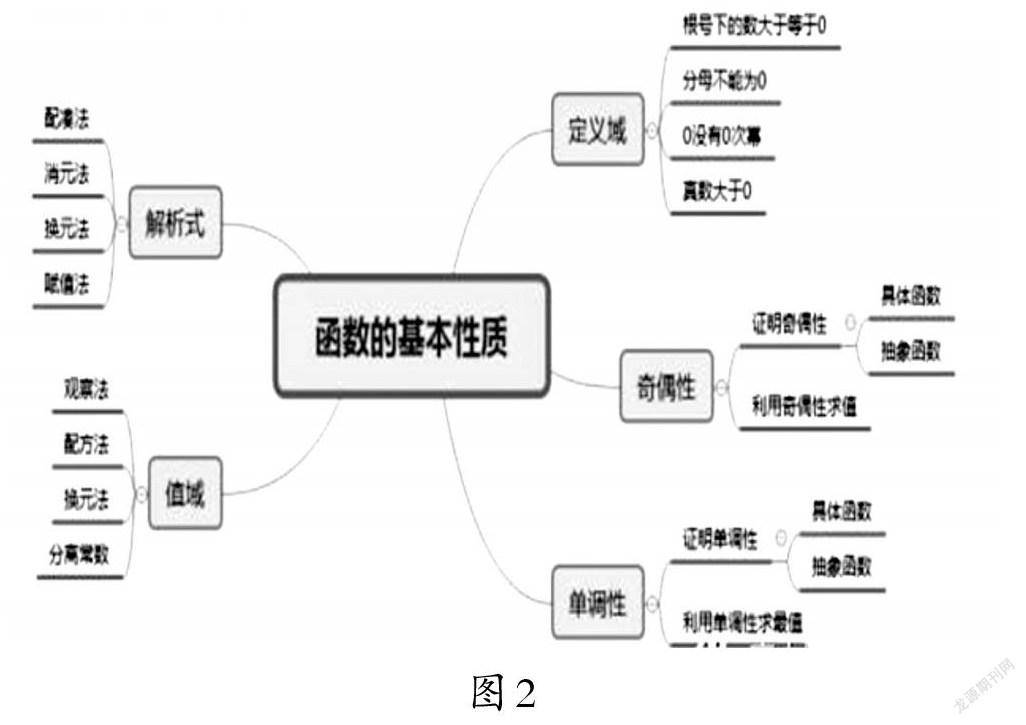
例如,在复习《函数的基本性质》时,笔者引导学生逐步回忆了函数的解析式、定义域、值域、奇偶性、单调性,并绘制了如图2所示的思维导图.引导学生寻找求函数解析式的方法:配凑法、消元法、换元法、赋值法,以及求函数值域的方法:观察法、配方法、换元法、分离常数法.再引导学生分析求函数定义域需要关注的方面:(1)根号下的数大于或等于0;(2)分母不能为0;(3)幂函数的底數不为0;(4)指数函数的真数大于0;等等.最后引导学生探讨了证明函数奇偶性、单调性的方法以及函数单调性、奇偶性的应用情况.
这样运用思维导图,引导学生由点集成面,将碎片化的知识整合起来,构建起清晰的、完整的函数知识脉络.学生通过该思维导图便能明确函数的基本性质的考查方式以及解题的思路,还可以通过思维导图中的关键词和核心内容来查找相应的知识、方法,以快速找到解题的思路,这样能大大提升复习的效率.
在复习的过程中,教师可引导学生运用思维导图对所学的知识进行查漏补缺,以完善知识结构体系.如在绘制思维导图后,要求学生将没有掌握的、理解的定义、公式、方法、性质等在图中标记出来,并在旁边标注相应的记号,对其进行深入地研究,以掌握该知识点.
总之,在高中数学教学过程中,教师利用思维导图辅助教学,将相关的知识关联起来,并以思维导图的形式呈现出来,不仅能加深学生对知识的理解,还能让其从整体上把握所学的知识、方法,有效地提升新授课、复习课的教学效率.
(作者单位:山东省聊城市茌平区第三中学)

