双车道异质交通波同步机理分析

潘守政，何 佳，王凤淇,2，贺正冰

(1. 北京工业大学 交通工程北京市重点实验室，北京 100124；2. 同济大学 交通运输工程学院，上海 200092)

0 引言

近年来，伴随着机动车保有量的增长，交通拥堵现象频发, 这不仅导致了居民的出行成本增加和交通事故频发，对社会经济和自然环境也造成了巨大破坏。探究交通拥堵的内在成因，有效地解决交通拥堵问题越来越成为研究人员关注的焦点。尤其在城市道路网中，多车道交通流往往具有复杂的交通特征与车辆运行的不确定性。探究该拥堵环境下的交通流特性受车辆驾驶行为影响的研究具有重要意义。在实际的交通拥堵路段，总会出现车辆走走停停的现象，这导致不同车道间的车流状态往往具有异质性，主要表现为当前车道处于排队状态，而相邻车道车流前进，此时通常会出现车辆的频繁换道现象。研究多车道拥堵环境中的换道行为对交通流特性的影响过程，对于判别交通运行状态、探索交通拥堵的传播规律、研究交通拥堵的疏导策略、指导瓶颈路段的管控方法具有重要意义。

在拥堵路段，通常会出现交通振荡现象，表现为车辆反复出现减速然后加速的走走停停的行驶。许多研究表明，换道操作对于交通振荡的演化有重要影响。Zheng等[1]通过分析高速公路碰撞数据，指出交通拥堵中的交通震荡对车辆安全有影响，而与之紧密联系的一个现象则是车辆的随机换道行为[2]。Ahn等[3]揭示了车辆换道会在相关车道形成交通震荡，并随着车道向上游传播。Jin[4]通过研究拥堵路段的交通状态，证明了车辆换道会使总体交通流产生瓶颈效应。Li等[5]比较了各种车辆类型和换道方向的换道影响，验证了交通状况与换道行为影响之间的定量关系。在这种换道行为影响下的交通振荡现象会极大地引起多车道路段交通流状态的异质性。

不同路段的交通流状态和传播规律也不相同[6]。拥堵路段中，换道对于走走停停波动现象的形成和传播也起到了重要作用。Kerner等[7]指出交通拥堵现象能长时间保持其结构和特征并在高速公路上稳定移动。Zheng等[8]研究发现换道是交通振荡的主要触发形式，同时使得交通流的局部扰动扩大为实质性波动，这表明换道及交通震荡会联合引起交通波的横向和纵向传递。但是这种规律的成因和最终导致的结果还没有得到广泛关注。

此外有学者研究发现，车辆换道对于不同车道的影响是不同的，如Wang等[9]采用微观的方法研究车辆换道行为，指出换道对驶入车道和驶出车道的影响是不平衡的，并且这种不平衡会向上游传播，同时换道对周围车辆的运行也有很大影响。Smith[10]指出换道会破坏车辆原有的跟驰特性，并在换道后逐步恢复到原来的状态。Munjal等[11]将扩展交通运动波理论应用在换道模型中。姚荣涵等[12]通过分析启动波和停车波传递的运动学特性，提出了参数意义明确，并且符合实际的运动学启动-停车波模型，但还没有考虑车辆换道的影响。

另一方面，在瓶颈拥堵路段中的交通流的同步现象也先后在仿真[13]和实际场景中[14]被发现。然而该现象与车辆的换道行为有何种关联？如何引起的车流同步趋势？相关研究都是在宏观上进行时空特征的分析，具体成因的微观解释少有人关注。因此，本研究以双车道场景为例，考虑换道行为在拥堵路段引发的车流波动现象对异质交通波的同步机理进行解析。首先通过仿真试验，识别出车辆换道行为对双车道异质交通波的同步现象，基于此建立车辆换道行为模型和交通波同步模型，分析不同换道行为对异质交通波传递的影响。最后通过仿真试验，验证各种换道行为对于不同交通波状态的影响，并得出了异质交通波中的同步规律。

1 换道影响下的交通波同步现象

在实际的交通拥堵路段，车流中会经常出现车辆减速再加速的走走停停现象，并向上游传播。在多车道环境下，这种走走停停现象的传递会导致不同车道间的交通流状态具有异质性。如驾驶员在当前车道行驶时，遇到拥堵排队，而相邻的车道处于畅通状态。此时有些驾驶员选择换道行驶，原有的走走停停的纵向传递形式被打破，换道使得2个车道的交通波产生了横向相互作用。在现有的车辆轨迹数据中，能够观察到这种现象，如在多车道的车辆轨迹时空图中，不同车道会具有不同形式的交通波传递。特别地，相邻的车道会出现相似的交通波传递现象，并且这些位置通常伴随着车辆的换道行为。然而，由于很难找到较大范围内的高精度车辆轨迹数据对该现象进行分析，因此，本研究采用元胞自动机[15-16]，通过较大范围的交通流仿真数据，对换道行为影响双车道异质交通波的同步机理展开研究。

1.1 试验场景设置

本研究以Rickert等[17]改进的NaSch双车道元胞自动机模型为基础，考虑实际车辆的减速概率与车速有关及安全因素[18-20]，加入一种速度的随机化(VDR)模型[16]，其减速概率即延迟概率p(v)依赖于车辆速度而变化。如式(1)所示，对于停止的车辆减速概率p2较大，行驶中的车辆减速概率p1较小，即：

(1)

同时，在模型中设置了车辆的换道概率参数，以模拟不同的驾驶习惯。gap(j)和l分别为当前车道前方车辆间距和安全车距，gapo(j)和lo分别为相邻车道前方车辆间距与安全车距，gapo,back(j)和lo,back分别为相邻车道后方车辆间距和安全车距，同时在模型中设置车辆选择换道的概率pchange，rand(j)为0到1的随机实数，则在双车道情境下，第j辆车的换道条件为：

(2)

1.2 异质交通波同步现象

车辆在瓶颈路段运行时，会因扰动产生拥堵现象，以交通流疏密波的形式向上游蔓延。以交通密度的变化在宏观上分析换道行为对双车道交通波的影响，绘制了换道时间点前后时间段拥堵路段中不同检测点处(换道前后各3处)的密度-时间图像。对比其中最远的2处检测点(下游检测点6和上游检测点1)的密度变化，见图1。

图1 检测器处的密度-时间图像Fig.1 Density-time image at detector

在禁止车辆换道的下游路段(见图1(a))，2条车道的交通流特征具有明显异质性，并具有不同的交通振荡现象，不同车道产生的交通波各自沿着当前车道向上游传播。在时间pchange=1之后，允许车辆换道，部分车辆从车道1换出驶入密度较低的车道2，并对车道2的交通振荡产生了影响。在上游的检测器1处(图1(b))，可以观察到两车道的交通密度变化呈现一定的同步趋势。

为了保证仿真结果的精确性，使用更大量的车辆轨迹数据进行分析，并取2 000～5 000 s (pchange=0)和5 000～10 000 s (pchange=1)数据，分别计算各个检测器处的两车道交通密度差值的平均数。如图2所示，允许换道相比于禁止换道，两车道密度差值的平均值总体更低。在禁止换道时，两车道交通密度的差值平均为20.9 vel/(km·ln)。允许换道时，两车道交通密度的差值平均为7.9 vel/(km·ln)。在换道影响下，两车道的交通密度更加接近。换言之，由于交通波能够体现同一车道不同状态交通流相遇时二者的形态转化，换道操作使得两车道交通波传递显现出更强的同步性。此外，由于交通波一般向上游传播，在研究路段尾端(下游路段)会检测到平均密度差趋向于中间值(图2)。

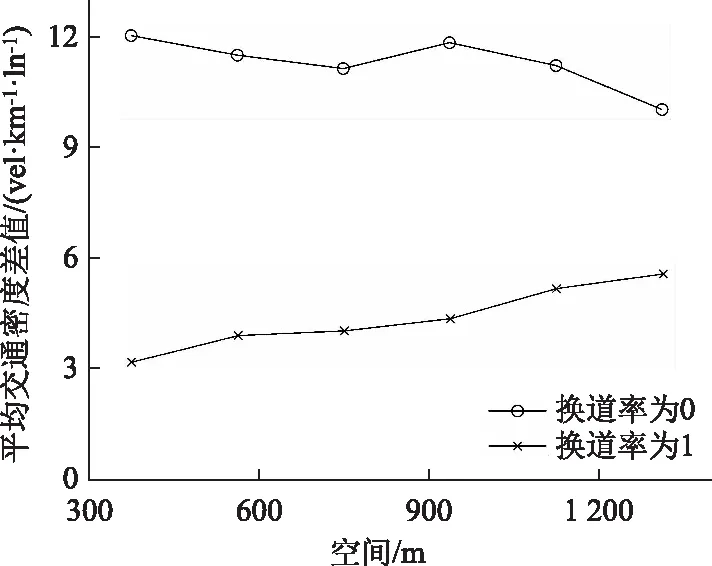
图2 各检测点车道间的平均密度差值曲线Fig.2 Curves of mean density difference between lanes at measuring points

2 双车道异质交通波同步模型

由上节可知，宏观上，双车道异质交通波在换道影响下具有同步趋势。为对该同步现象机理进行探究，建立车辆换道影响下的交通波模型，以在微观上对该现象进一步分析。首先，将换道行为分为换出当前车道和换入当前车道2类，然后建立换道对不同状态交通波的影响模型，包括停车波、启动波、拥堵段和自由流段。

2.1 换道影响下的交通波模型

车辆换道行为可分为换出当前车道和换入当前车道2种。而车流状态可划分为行驶、减速、停车、启动4类，对应车辆轨迹时空图中的自由流、停车波、拥堵段和启动波部分(图3)。基于此分别对上述4种区域下的2种换道行为对交通波的影响进行分析，建立换道影响下的交通波模型。

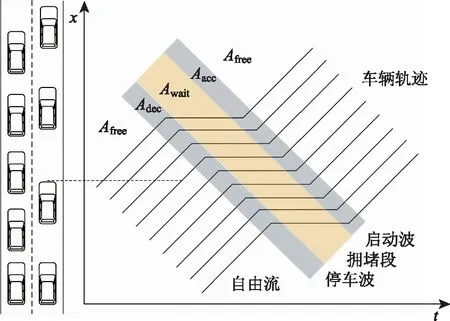
图3 时空轨迹图的区域划分Fig.3 Regional division of spatio-temporal trajectory

考虑到车辆在换道时会对前后方车流产生影响，结合运动学定律和车辆时空演化规律，以车流的速度变化-交通波波速为主要特征，对车辆换道前后波速的变化情况进行研究。首先是车辆换出对启动波(Aacc区域)的影响，如图4所示，第n+1辆车在t=tc(tc<0)时从该车道换道驶出，在t=0时第n辆车以加速度行驶，在时间τ后获得最终速度ust，车辆到达道路前方某位置P的时刻为tn，行驶距离xn。假设车辆加速特性相同，第n+2辆车在第n辆车启动Δt′后以加速度a行驶，在时间τ后同样获得最终速度ust，在tn+2后到达同一位置P，行驶距离xn+2。

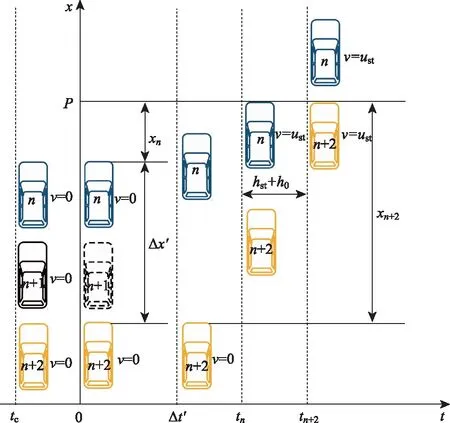
图4 车辆换出时启动波传播过程示意图Fig.4 Schematic diagram of starting wave propagation when vehicles moving out

第n辆车和第n+2辆之间的停车间距即启动波传播的距离Δx′，其与阻塞密度kj的关系为：

(3)

由运动学定律，可得到由饱和车头时距hst和参数ho表示的第n+2辆车的启动时间：

(4)

利用启动波传播的距离和时间，可得到换道影响下的启动波波速u′wst,exit为：

(5)

而无换道环境下的启动波波速为[12]：

(6)

在第n+1辆车换道驶出的模型中，从第n+1辆车驶出车道至第n+2辆车起步的时间为：

Δtn+1,n+2=Δt′-tc。

(7)

由于第n+1辆车换道驶出会给第n+2辆车更大的车辆间距，使得第n+2辆车启动的时机相比无换道环境中的启动时间Δt提前，因而有Δtn+1,n+2>Δt，据此可得到：

(8)

当车辆在车队启动波附近换出车道时，启动波速度将增大，向车流运行反方向加速传播。在时空图上会呈现启动波的弯折，表现为启动波在短时间内向上游漂移一定的距离，如图5(a) 中所示，图中密虚线表示换道车辆轨迹。

同理，可得到车辆换出对停车波(Adec区域)影响的判断模型。该场景下，无换道的停车波速度uwsp与换道影响下的停车波速度usp大小关系有：

(9)

式中，usp为车辆初始速度；ksp为停车波后方平均密度；kj为停车波前方阻塞密度；a为第n辆车的减速度(a>0)；a0为第n+2辆车的减速度(a>ao>0)；τ为车辆制动时间。

即车辆在停车波附近换出车道时，该车道的停车波速度减小，向车流运行反方向传播速度变慢。在时空图上同样展现出停车波的弯折，表现为车辆换出使停车波在短时间内向下游漂移一定距离，如图5(b) 所示。

其次是车辆在排队中(Await区域)换出的情况。当车辆在拥堵排队路段中换出时，从换出位置开始，后车会逐步向前行驶一个车位的距离，然后减速停车继续等待，这种情况下的前进停车的状态将以固定的速度向上游传播。如图5(c) 所示，在排队队列中产生了新的停车波与启动波。然而，这些交通波仅短暂地影响波面前后的少许车辆，对距离较远的停滞车辆几乎没有影响。因此该区域下的换道行为不会产生显著的交通波变化。另外在自由流中，正常车辆也不会发生换出车道行为，可排除该情况。

图5 车辆换出时不同交通波变化和试验车辆轨迹Fig.5 Changes of traffic wave and track of experimental vehicle when vehicles moving ou

对于车辆换入的情形，正常情况下只有换入车道的交通状态良好时驾驶员才会考虑换入。此时换入车道会产生新的停车波(Adec区域)，车流速度也会受到影响。而这种现象可能会重复出现，即车辆原所在车道遇到拥堵，车辆随即换入相邻车道以求得更好的驾驶体验，之后在相邻车道有可能会再次遇到拥堵，再换入原来车道。对于任意2辆相邻的车辆，忽略车辆间驾驶差异，可得无换道的停车波速度uwsp与车辆换入影响下的停车波速度u′wsp,enter大小关系：

(10)

式中λ(λ>0)为固定参数。

当车辆换入当前车道后，停车波速度将变大，此时在时空图上表现出停车波在短时间内向下游漂移一定距离。将换道影响下的波速与原有停车波速度相比较，换道点附近会产生减速的现象，如图6(a) 中所示，图中密虚线表示换道车辆轨迹。

在自由流状态下，也会发生车辆换入的行为，并对换入车道的交通状态产生影响。由于瓶颈路段的自由流会接近饱和，车辆的行驶速度受到限制。此时车辆换入会使该车道的后方跟驰车辆减速或停车，进而造成车流短暂的停顿与启动，并产生新的交通波传递，如图6(b) 所示。

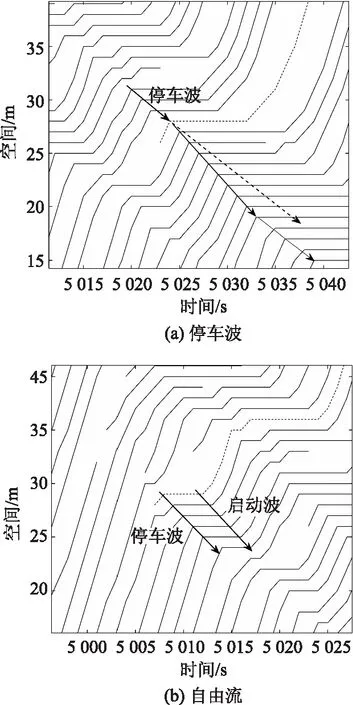
图6 车辆换入时不同交通波变化和试验车辆轨迹Fig.6 Changes of traffic wave and track of experimental vehicle when vehicles moving in

结合以上模型分析，可以得到双车道情景下异质交通波受换道影响的变化规律，如表1所示。而交通波的变化可总结为图7所示的2种情况。基于此定义了交通波时空变化的函数以进行定量化描述。波面在道路上位置的时间函数为x=Wi(t)，其中i为车道数。在车辆j换道(换出或换入)影响下，交通波传递特性出现不稳定状态(图7)。之后，重新稳定的交通波波面的位置-时间函数变为：

x′=W′i(t)。

(11)

相较于未受换道影响下的交通波，新的波传递在时空图上产生了时间tj和空间xj的漂移，二者关系可表示为式(12)，当tj<0,xj<0时，换道处交通波加速传递。

x′=W′i(t)=W′i(t-tj)+xj。

(12)

表1 换道对交通波的影响Tab.1 Influence of lane changing on traffic waves

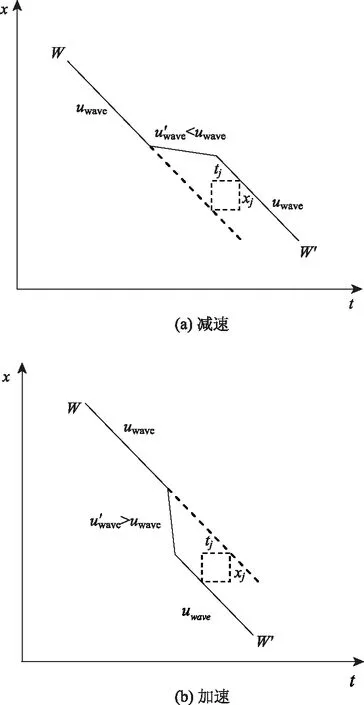
图7 换道影响下的交通波传递Fig.7 Traffic wave transmission under influence of lane changing

2.2 异质交通波同步原理

基于双车道异质交通波中的同步现象，考虑同一时间不同车道的区域状态的空间位置关系，提出了一种判断异质交通波是否具有同步趋势的理论依据，并根据2条车道的不同交通流状态，划分出4种异质交通波形态。对于给定的停车波i或启动波Δx′sp-Δxsp在时空图中的传递特性，将波面在第i条车道中的位置的时间函数表达为：

(13)

研究换道对异质车流波动的影响，主要对图3中3种区域组成的拥堵路段进行分析。对于双车道异质交通波，随着时间变化，2条车道交通波波面之间的距离也在发生改变。在未受到车辆换道影响时，2条车道交通波(分为停车波与启动波)分别在道路上传播时的波面位置差的时间函数为：

(14)

当车辆换道后，2条车道的交通波分别受到车辆换出和换入影响产生波动，一段时间恢复稳定后分别计算两车道停车波和启动波波面之间的距离Δx′sp和Δx′st。据此，定义该模型下双车道异质交通波是否具有同步趋势的依据为：

若两车道的交通波(停车波或启动波)波面的位置差减小，即Δx′st-Δxst<0或Δx′sp-Δxsp<0，则双车道异质交通波有同步趋势。

而当有：

(15)

双车道交通波将到达同步状态，其中εsp和εst是依据真实轨迹数据标定的距离参数，表示两车道交通波同步时波面在路段上可接受的距离。

2.3 异质交通波形态定义

在双车道异质交通波的时空轨迹图中，根据2条车道临近的启动波与停车波波面之间的距离，将双车道异质交通波形态划分为了以下4种：临近态、重叠态、包含态、有无态，如图8所示。并定义每种状态如下。

临近态：2条车道的拥堵排队路段临近，表现在上游的启动波与另一车道下游的停车波之间有一定距离。

重叠态：2条车道的拥堵排队路段有重叠位置。

有无态：1条车道有拥堵现象另一车道为自由流。

在瓶颈路段，临近态、重叠态和包含态都呈现出双车道拥堵现象，以拥堵的空间位置差异来区分。而有无态其中1条车道为畅通状态，见图8(d)。

3 双车道异质交通波的同步过程

基于上节建立的换道影响下的异质交通波模型，采用交通仿真的方式，通过较大范围的交通流仿真数据，在微观上对换道影响下的双车道异质交通波的同步过程进行验证分析。利用判别模型，分析不同换道行为对于交通波状态的影响及不同状态间的转化趋势。

3.1 异质交通波同步趋势

在双车道场景下进行瓶颈路段交通流仿真。根据第2部分中的划分，在车辆轨迹图中可以识别出4种异质交通波状态，如图8所示。

针对不同类型的交通波状态，研究了不同的换道位置对2条车道交通波变化的影响。并依据上节的同步趋势的判别依据，得到如表2所示的分析结果。情景1为临近态，情景2为重叠态，情景3为包含态。未满足换道条件的情景没有列出，而有无态的交通波变化形式有所不同，将在下一节进行分析。SPWi为第i车道的停车波，STWi为第i车道的启动波。加速或减速选填项表示交通波受换道影响产生图7中的2种情况。研究表明，车辆在双车道异质交通流中换道时会引起不同车道交通波状态的变化，并逐渐产生同步趋势。该趋势不仅与2条车道的具体交通状态之间的空间关系有关，还与车辆换道的位置有较强的关联性。

表2 换道对双车道异质交通波的影响Tab.2 Influence of lane changing on two-lane heterogeneous traffic waves

3.2 不同交通波形态转化

分别对每个状态下的车辆轨迹进一步研究。发现随着时间变化，受换道行为影响的异质交通波的不同状态之间具有定向的转化趋势。当双车道异质交通流处于临近态时，由于车辆换道，交通波形态在空间上逐步靠近，车辆排队位置也逐渐重叠。当2条车道的停车波或启动波波面之间距离足够近时，2条车道交通流中的车辆减速、排队与行驶状态会呈现出相似性，异质交通波受换道影响而趋向同步，如图9(a) 所示。另外，当2条车道交通流处于有无态时。在自由流车道中会产生新的停车波与启动波，从而形成了包含态的异质交通波。此时2条车道的启动波和停车波在空间位置上逐步靠近，并最终趋于同步，如图9(b) 所示。

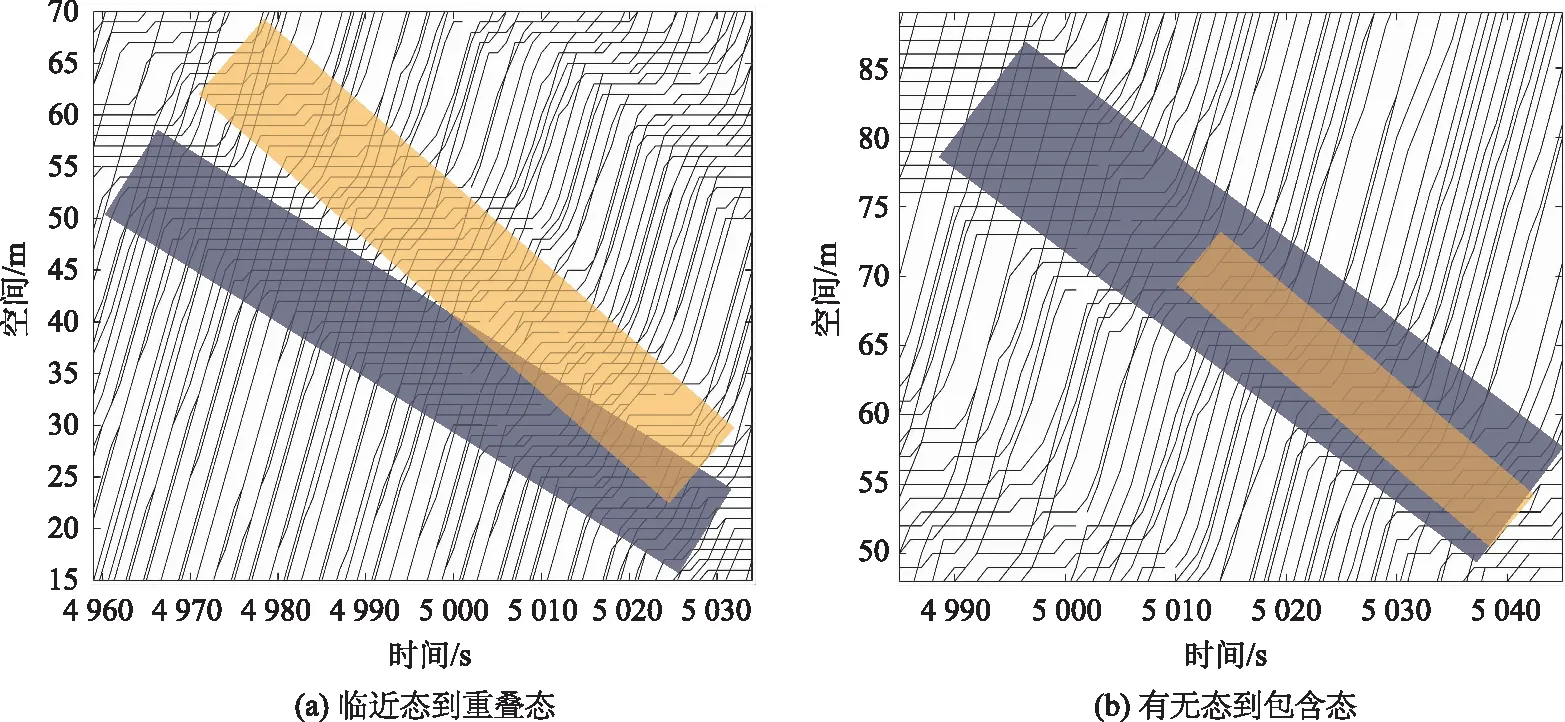
图9 双车道异质交通波形态转化Fig.9 Transformation of dual-lane heterogeneous traffic wave forms

试验结果如图10所示，换道影响下的双车道异质交通波在时空轨迹图上呈现的4种状态之间可进行定向转化，并最终趋于同步。

后期，白羽令散发得更为随意，有一半左右的白羽令，是盟中游侠想找个一起喝酒的对象，插白羽看看附近有没有同盟中人。

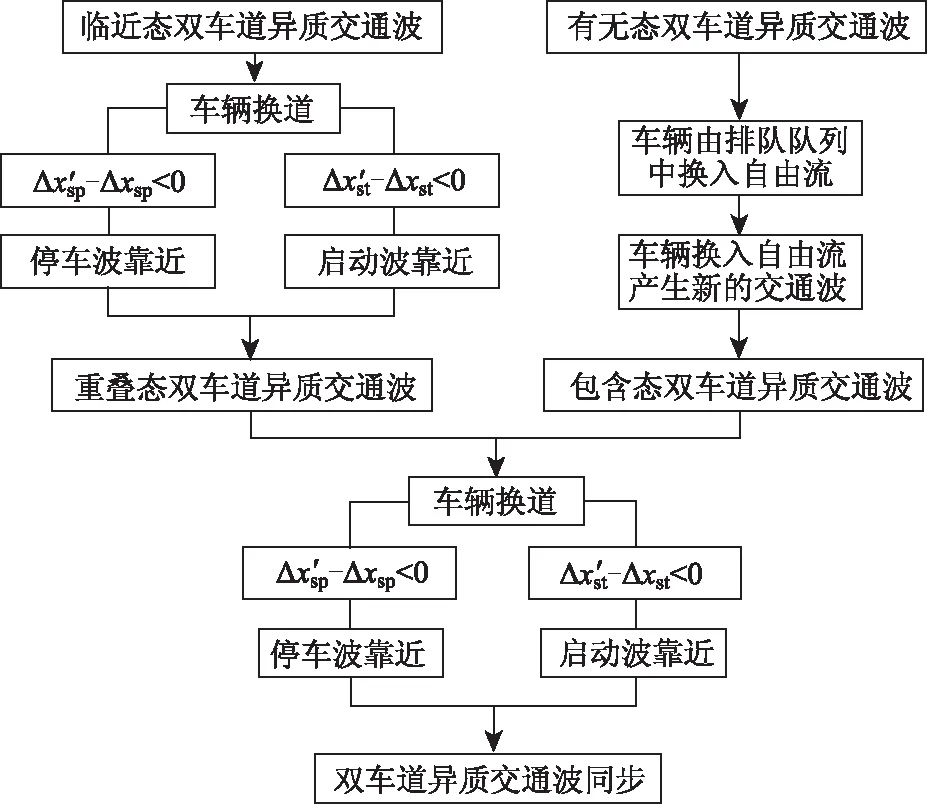
图10 双车道异质交通波同步过程Fig.10 Synchronization process of dual-lane heterogeneous traffic waves

4 结论

双车道环境下2列车流的运行特征往往具有异质性，主要表现为当前车道拥堵停滞，而相邻车道通行较为顺畅，此时换道行为多发。当到达瓶颈路段，车辆换道会使得交通流中会反复出现车辆减速，之后加速的交通振荡现象，同时产生停车波与启动波在道路中的横向和纵向传递，最终出现交通波同步现象。本研究通过构建交通波传递模型，从宏观和微观上分析了换道行为是如何影响双车道异质交通波变化和传递的。对不同车道交通波之间受到影响时的变化特征和演化机理做了较为深入的探究。最后使用仿真试验，对双车道环境下的换道行为对异质交通波的影响进行了分析验证。通过建立车辆换道影响下的交通波模型，发现车辆换道对交通波传递速度具有显著影响，而速度的变化与车辆换道在交通流中的位置密切相关。此外换道行为会使不同车道的交通波传递波面有相互靠近的趋势，在宏观和微观交通流特性上具有同步趋势。

当然，本研究只对双车道的换道行为进行了研究，未来还可以继续分析更多车道场景。同时，还可以借助现实中的车流数据来进一步验证。在这种换道行为影响下，车流波动对最终的道路运行状况起到了何种效果，是否加剧了拥堵等也值得研究人员进一步去思考。