榆林地区降水特征分析及降水量预测
王大浩,方亚宏,李金龙,柯贤敏
(1.长安大学 水利与环境学院,陕西 西安 710000;2.长安大学 旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054)
在水文和气象学中,一个地区的降水量往往是该区域水资源状况的决定性因素,对工农业生产和社会经济发展有着显著影响。大气降水作为水资源的直接补给源,可以直观地反映区域水资源的丰富程度,也是水土流失、洪涝灾害的主导因素[1-2]。因此,降水量的变化特征分析及科学预测是了解一个地区变化环境中的水量变化及其演变规律的重要手段。其中,Mann-Kendall非参数方法(M-K法)及有序聚类分析法等是降水时空分布特征分析的常用方法[3-5]。周文婧等[6]采用M-K法对巴尔喀什湖流域的降水变化特征进行分析,表明该流域的降水在年内分配上无显著变化。张昌顺[7]利用有序聚类分析法对甘肃省水面蒸发量分布特征及演化规律进行了系统研究。袁满等[5]指出传统有序聚类法只考虑同类之间离差较小的原则,忽略了同类之间离差较大的原则,并提出了可以修正结果偏差和遗漏的有序聚类法的改进方案。加权马尔科夫链预测模型和模糊集理论被广泛应用于区域降水量的预测中,钱会等[8]采用加权M-K法预测模型对石嘴山市2009年和2010年的年降水量进行预测,预测值分别为135.11 mm和146.88 mm。屈文岗等[9]使用加权马尔科夫链预测模型等方法,预测华山地区未来10 a的降水量均值为767.32 mm。杜川等[10]利用模糊聚类算法对加权马尔科夫链预测模型进行改进,提高了模型的预测精度。
榆林市地处我国西北内陆,地貌独特,地形较为复杂。受降水与地形的影响,榆林市旱涝灾害频发。除此之外,榆林市是我国为数不多的能源矿产富集区,这种由降水量时空差异性引起的水资源分布不均,很大程度上限制了当地能源矿产的开发与利用,也严重制约了当地经济的可持续发展[11]。然而,关于榆林市区域降水量变化特征分析的相关研究较少,而且并未对未来降水量进行预测。鉴于此,笔者在全面收集榆林市气象资料的基础上,采用M-K法分析降水量变化趋势,并用改进的有序聚类分析法检验突变点,以加权平均马尔科夫链预测降水状态,并用模糊集理论计算出具体的预测值,用实测值加以验证。
1 研究区概括
榆林 地 区 地 处 东 经107°28′—111°15′、北 纬36°57′—39°35′之间,位于陕西省最北部。榆林地区属于典型的温带大陆性气候区,春季干燥少雨,夏季潮湿炎热,秋季温润凉爽,冬季寒冷干燥。该地区多年平均气温为8.1℃,月平均气温在1月最低,为-9.7℃,7月最高,为23.3℃。该地区多年平均降水量为387.2 mm,降水集中在夏季。
2 资料与方法
2.1 降水资料
选用榆林气象站1951—2015年逐日降水资料,该数据来源于中国气象科学共享服务网和榆林市气象站。
2.2 研究方法
2.2.1 降水特征分析与突变分析方法
降水的时序特征具有一定的区域性、趋势性[12]。采用M-K法和改进后的有序聚类法对榆林市降水序列的分布特征和突变情况进行分析。M-K法已被广大学者用来分析降水、径流和温度等要素的时序性变化,其检验不需样本遵从一定的分布,较为适合分析检验水文、气象等非正态分布的时间序列数据,计算也较为简单[13]。有序聚类法是分析降水序列突变点的有效方法,本文采用的是袁满等改进的有序聚类法,与改进前的方法相比,具有识别的突变点精度更高和能够识别出边缘突变点的特点,其改进过的目标函数如下[5]。

式中:τ(2≤τ≤n-1)为水文序列(x1,x2,…,xn)的突变点,即突变前序列的长度;d为类与类之间的离差;στ及σn-τ为同类之间的均方差;ˉxτ和ˉxn-τ分别为突变前后两个序列的均值。
2.2.2 降水量预测及验证方法
气象条件的复杂性和多样性决定了降水过程存在很大的不确定性。以降水量时间序列的自相关系数为权重,利用加权的马尔科夫链预测模型对榆林地区未来降水量丰枯变化状况进行预测,同时使用模糊集理论计算具体的降水量预测值,再结合实际数据进行误差分析来验证模型的精度。其中,马尔科夫过程是随机过程的一个分支,其数学表达见文献[14-18],本文不再赘述。模糊集理论既能综合考虑其他概率对实际预测的影响,又可以在确定预测对象在区间大致位置的同时,求解出其具体值。以本研究为例,首先对降水状态赋以相应的权重:

式中:i为降水状态编号;pi为降雨状态为i的概率;z为其最大概率的作用指数,一般取2[3,8-9]。
当确定了最大概率状态时,便可以利用模糊集理论计算出一定时段内的预测值,即

式中:Ti和Bi对应最大概率状态区间的最大值和最小值。
3 降水特征分析
3.1 年内变化分析
榆林地区1951—2015年月平均降水量如图1所示,由图1可知:榆林地区降水年内分布极为不均,主要集中在夏季,占全年降水量的65.05%;8月平均降水量最大(占年均降水量的27.64%,为109.46 mm);12月降水量最少,为1.15 mm,仅占年均降水量的0.29%。由表1可见榆林地区降水的年内分布较为离散,夏季的降水量决定了全年降水量的多少。
由表3可知:船员主观感受中所有条目的平均值均≤3,说明船员在超劳和加班的情况下感受不愉快,在加班及超劳时感受费力和压力。

图1 榆林地区1951—2015年月平均降水量

表1 榆林地区1951—2015年季节平均降水量统计
榆林地区年内季节降水趋势如图2所示,可知四季的降水量均呈上升趋势,其中夏季递增速率最大,为6.72 mm/10 a。春季递减速率最小,为1.25 mm/10 a。通过M-K法解得的统计检验量Z值见表1,分别为0.861、0.503、1.358、6.960,说明年内降水量的趋势检验结果与线性趋势分析的结果吻合。

图2 榆林地区1951—2015年季节降水趋势变化
3.2 年际变化分析
结合榆林地区1951—2015年降水量分布特征和降水量变化曲线(见图3)可知,榆林地区年均降水量为387.2 mm,1964年降水量最大(为661.1 mm),1965年降水量最小(为142.8 mm),极值比高达4.63,可见其降水量年际变化较大。榆林地区年降水量处于波动状态,整体呈递增趋势。使用M-K法对其进行趋势分析可得,榆林地区年降水量的Z值为1.40,表明该检验通过了可信度为90%的显著性检验,线性趋势分析结果与其一致。

图3 榆林地区1951—2015年年降水量变化趋势
3.3 降水突变分析
分别采用传统有序聚类法和改进的有序聚类法对年降水量序列进行了突变分析,如图4所示,S0(t)为传统有序聚类法计算的S值,S1(t)为改进后的有序聚类法计算的S值。改进的有序聚类法识别出在2000年和2011年降水量发生了突变,而传统有序聚类法未能识别出2000年为降水突变年,由于2000年和2011年均为距离时间序列末项不足20项的边缘突变点,因此采用突变点前后序列的离差对突变显著性进行检验。从表2可知,2000年前后离差为96.445,2011年前后离差为173.331,两点的突变性均是显著的,说明改进后的有序聚类法比传统方法精度更高,可以识别出传统方法中遗失的降水突变点。

表2 离差及突变点显著性检验
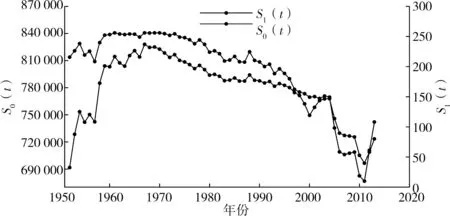
图4 榆林地区1951—2015年年降水量突变分析
年际降水量离差平方和最小的情况出现在2011年,根据《陕西省统计年鉴》记载,2011年为降水极端异常年,分析所得结果与实际情况一致。2011年之前的年降水量均值为380.5 mm,2011年以后其值为553.8 mm,相差173.3 mm,可知年降水量呈增长趋势,该结果与降水量变化曲线分析的结果一致。
4 榆林地区年降水量预测
4.1 模型检验
根据降水频率分级标准,确定了榆林地区1951—2015年3 a滑动平均降水量的等级划分(见表3)。分别用1951—2013年和1951—2014年的3 a滑动平均降水量对2014年和2015年的滑动平均降水量进行预测(见表4、表5),并通过模糊集理论的级别特征值计算具体的预报值,分析结果与误差分析见表6。由表6可知,在中长期水文预报时,相对误差要小于20%[19]。因此,榆林地区2014年和2015年的滑动平均降水量预测均满足对应的精度要求。总之,加权平均马尔科夫链模型预测榆林地区降水量的方案可行。

表3 1951—2015年3 a滑动平均降水量的等级划分

表4 榆林地区2014年3 a滑动平均降水量预测

表5 榆林地区2015年3 a滑动平均降水量预测

表6 榆林地区2014—2015年3 a滑动平均年降水量预测结果及误差
4.2 降水量预测
基于上述加权平均马尔科夫链预测模型及模糊集理论,对榆林地区2016—2025年的降水量进行预测,预测结果见表7。由表7可知,未来10 a内的降水量呈增加趋势。未来10 a内预测降水量均值为433.2 mm,增加速率为47.0 mm/10 a,预计在2024年出现最大预测值,为460.2 mm;2019年出现最小值,为417.7 mm。

表7 榆林地区2016—2025年降水量预测
4.3 遍历性与平稳分布

式中:j为降雨状态;πj为降雨状态为j的极限分布概率。
极限分布概率πj和各状态出现的周期Tj,二者满足Tj=1/πj,结果见表8。
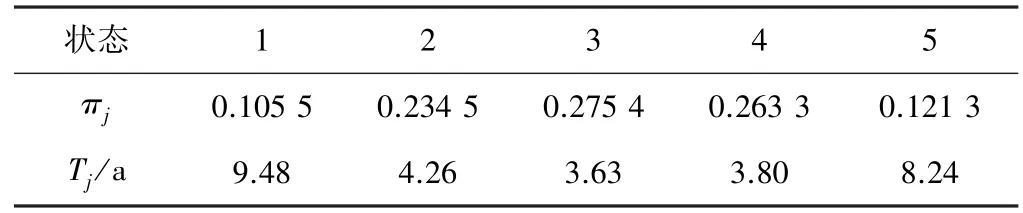
表8 极限分布与状态周期
结合降水频率分级标准与表8可知,在1951—2015年中,榆林地区正常降水年份出现的概率为0.275 4,出现周期为3.63 a;干旱年份出现的概率为0.105 5,出现周期为9.48 a。
5 结 论
(1)榆林地区年内的降水分布不均,降水主要集中在夏季。年内各季节降水均呈上升趋势,其中:夏季递增速率最大,为6.72 mm/10 a;春季递增速率最小,为1.25 mm/10 a。M-K法求得的春、夏、秋、冬Z值分别为0.861、0.503、1.358、6.960,说明年内降水量的趋势检验结果与线性趋势分析的结果吻合。
(2)榆林地区降水年际分布极为不均。M-K法分析可得,整体年降水量处于波动状态,整体呈递增趋势,通过了可信度为90%的显著性检验。
(3)对比改进前后的有序聚类法对突变的分析结果,改进的有序聚类法对突变点的识别更加精确。降水序列的离差平方和最小出现在2011年,说明年降水量序列在该年发生了突变,该结果也与实际情况一致。
(4)基于降水频率分级标准将榆林地区1951—2015年滑动平均降水量进行状态分级,建立了加权马尔科夫链预测模型,运用部分年份降水量资料和模糊集理论方法验证了该模型的可靠性。
(5)预测结果表明,榆林地区未来10 a内预测降水量均值为433.2 mm,增加幅度为47.0 mm/10 a,预计在2024年出现最大预测值,为460.2 mm;2019年出现最小值,为417.7 mm。根据马尔科夫链遍历性原理,计算出了榆林地区1951—2015年降水量的极限分布,表明榆林地区年降水量处于平水年的可能性较大,平均每隔3.63 a出现一次。

