基于S-Euler-Elastic模型的彩色图像乘性噪声去除方法研究
王启帆,潘振宽,魏伟波
(青岛大学计算机科学技术学院,青岛 266071)
图像噪声去除是图像恢复中的一类经典问题,有学者首先提出的Tikhonov模型[1]为之后的图像处理奠定基础,该模型包含了数据项和规则项,虽提高了计算效率,但经由Tikhonov 模型处理后的图像会产生边缘模糊的问题。针对该问题,1992年,Rudin[2]提出了TV( total variation)规则项,有效实现了边缘保持。
1 相关研究
1.1 低阶去噪模型
图像噪声方面的研究主要包括对加性噪声和乘性噪声的研究。在图像处理中对于加性噪声的研究较多,相对而言比较成熟,对于乘性噪声的问题的研究非常少,这类问题通常会转化成加性噪声的形式进行处理,导致对乘性噪声的去除效果不够理想。为了更好地解决乘性噪声的相关问题,基于一阶TV模型提出了乘性高斯(Gaussian)噪声分布的RLO模型[3],能量泛函为
(1)
由于RLO模型无法有效地清除乘性伽马噪声,因而提出了针对乘性伽马噪声的AA模型[4],能量泛函为
(2)
上述的两种噪声模型针对的只是单一乘性噪声的处理,SO模型[5]对于模型中的a,b,c取不同的值时可以应用于不同类型的乘性噪声,其能量泛函为
(3)
其中,a,b,c为常数且c=a+b,a,b≥0,λ和α是惩罚参数。在该模型中,第一项为规则项,第二项是数据项,a,b,c取不同的值分别代表乘性高斯噪声、乘性瑞利噪声、乘性伽马噪声的噪声分布。
1.2 彩色图像去噪模型
上文提到的模型大多是针对灰度图像,虽然彩色图像可看成由多层灰度图像构成的,但直接处理时由于多层图像扩散程度不同会造成边缘模糊。故针对彩色图像噪声处理问题学者提出了相关模型。
在文献[6-7]基础上,提出了基于全局耦合的CTV模型[8]能量泛函为
(4)
图像局部耦合的MTV模型[9-10]能量泛函为
(5)
由于考虑了图像的层与层之间的耦合关系,MTV模型可以更好地保持彩色图像的细节等边缘信息。
1.3 高阶去噪模型
关于图像去噪问题的处理,大多为低阶去噪模型,且以一阶TV规则项的应用最为广泛,但因一阶去噪模型图像中存在严重的阶梯现象,故使用高阶模型来处理图像噪声问题。
Hessian模型[11]被用来解决相关的乘性噪声问题,能量泛函为
(6)
虽然该模型可以保持图像的光滑度,但在图像对比度保持方面较差。
为了解决以上问题,又提出了关于图像去噪的TGV模型[12],能量泛函为
(7)
之后,Goldluecke等[13-15]提出将TC作为规则项来修复图像,能量泛函为
(8)
此后TC模型应用也比较广泛,大多用于图像修复。
Euler-Elastic项是由Nitzberg提出[16],Elastic弹性项可以相对较好地进行图像的修复操作。Shen等[17]在图像修复中用到了这个理念,提出了Euler-Elastic 模型,能量泛函为
(9)
对于彩色图像,传统的去除乘性噪声的低阶或是高阶模型都存在或多或少的问题。CTV模型虽去噪效果较好,但存在边缘无法保持的问题,MTV虽能保持图像边缘,但会产生阶梯效应。为了解决上述问题,本文提出一种新的模型,将Euler-Elastic规则项与传统的去噪模型数据项相结合,在保证去噪的同时,可以有效地较少阶梯效应,并且保留图像的细节等其他信息。为了提高计算效率,本文主要采用Split Bregman算法来求解,通过引入多个辅助变量,将问题分解为多个单一变量的交替迭代求解问题,通过构造相关的Euler-Lagrange方程,在子问题中利用FFT等快速求解方法进行求解。
2 彩色图像去噪的S-Euler-Elastic模型及Split Bregman算法
本文提出S-Euler-Elastic模型去除彩色图像乘性噪声,设f(x)=(f1(x),f2(x),…,fm(x)):Ω→Rm,u(x)=(u1(x),u2(x),…,um(x)):Ω→Rm,其能量泛函
(10)

定义Bregman迭代距离(d1i,d2i,d3i,d4i)和4个正的惩罚参数(θ1,θ2,θ3,θ4),根据上文得到的约束条件,改写Split Bregman算法

(11)
式(11)中的Bregman迭代距离为
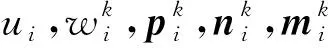
wk+1=argminE(uk,w,pk,qk,vk,sk),uk+1=argminE(u,ωk+1,pk,qk,vk,sk)
pk+1=argminE(uk+1,ωk+1,p,qk,vk,sk),qk+1=argminE(uk+1,ωk+1,pk+1,q,vk,sk)
vk+1=argminE(uk+1,ωk+1,pk+1,qk+1,v,sk),sk+1=argminE(uk+1,wk+1,pk+1,qk+1,vk+1,s)

(12)
离散化
(13)
分别引入恒等算子与移位算子,I为单位矩阵
再次离散化
(14)
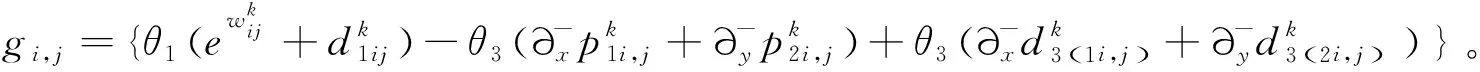
通过FFT,得
(15)
(16)

转换式(15)、(16),得
(17)
其中,Di,j=[θ1-θ2(2coszi+2coszj-4)]FFT(ui,j)=FFT(gi,j)
更新,使用FFT-1,得
(18)
求解w,可得Euler-Lagrange方程
(19)
根据以上方程求解w
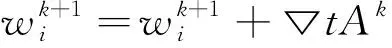
(20)
其中,▽t代表时间步长。
固定其他的变量来求解p,Euler-Lagrange方程为
(21)
转换使用软阈值公式变换式(21),得
(22)
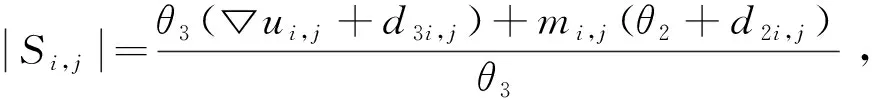
推导,得关于P的Euler-Lagrange方程为
θ4(ni-mi-d4i)-▽·(2b|pi|(▽·ni))=0
(23)
转换,得
-c▽(▽·ni)+θ4·ni=θ4(mi+d4i)-▽·[(c-2b|pi|)(▽·ni)]
(24)
其中,c=max(2bp(i,j)),接下来求矢量n的Euler-Lagrange方程

(25)

使用FFT求解
(26)

得到线性方程后,通过FFT-1,得
(27)
(28)
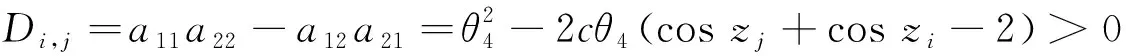
求解关于m的Euler-Lagrange方程,得
(29)
经投影方法处理,其中满足条件为|m|≤1
(30)
S-Euler-Elastic模型的伪代码:
1) 首先令K=0,且(u,w,p,n,m,d1,d2,d3,d4)=0, (α,β,γ,θ1,θ2,θ3,θ4)>0
2) While|Ek+1-Ek|/|Ek|<ε,do
由式(18),求uk+1;
由式(20),求wk+1;
由式(22),求pk+1;
由式(27)(28),求nk+1;
由式(30),求mk+1
End while
3 数值实验
实验在Inter(R) Core(TM) i5-4590 CPU @ 3.3GHz,4GB内存机器上运行,采用的编程环境为Matlab R2018b。将本文提出的S-Euler-Elastic模型与传统变分去噪模型在去噪效果、计算效率等多方面的对比,为了能更客观的比较各个模型的实验效果,还引入了两个图像对比指标:峰值信噪比PSNR与结构相似性指数SSIM。
3.1 定性分析
实验选择了3幅分别为Flower、Pepper以及ball的图像来比较CTV、MTV、TC、TGV模型与本文提出的S-Euler-Elastic模型在处理图像清晰度、色彩和对比度以及光滑度等方面的优缺点。设置了CTV、MTV模型的λ与θ初始参数分别为50、0.02。TGV模型的初始参数α1,α2,β1,θ1,θ2,θ3分别为5,10,10,15,15,25。TC模型的初始参数α1,θ1,θ2,θ3,θ4,θ5分别为10,10,15,15,20, 25。本文S-Euler-Elastic模型的α初始参数值为10,其余的参数值设置与TC模型的参数设置相同,且3幅图像的大小都是200×200像素,实验结果见图1~图3。

图2 乘性瑞利噪声去除对比(a)Pepper;(b)瑞利噪声;(c)CTV模型;(d)MTV模型;(e)TC模型;(f)TGV模型;(g)本文模型

图3 乘性伽马噪声去除对比(a)Ball;(b)伽马噪声;(c)CTV模型;(d)MTV模型;(e)TC模型;(f)TGV模型;(g)本文模型
由图1可知,CTV与TGV模型虽然能对原图像对比度和图像细节保持效果比较好,但却在花朵的边缘处产生模糊效应。MTV对比CTV虽无模糊的效应,但图像细节保持的不好,且产生了一定程度的马赛克效应。TC模型无模糊效果,也不会产生阶梯效应,细节保持也较好,但对于花朵花瓣处的清晰度还需要进一步的调整提升。本文提出的S-Euler-Elastic模型,避免了图像产生阶梯效应,并且图像的清晰度也得到了较好的保持,对比度也较好。
由图2可知,CTV模型与MTV低阶模型都会在产生一定程度的模糊效果,且二者对于图像边缘的处理以及噪声的清除效果都不理想。TGV模型在图像细节处理方面较好,但图像边缘模糊。对比以上几种模型TC高阶模型不会产生明显的模糊效果,但对于图像的清晰度还需要完善。S-Euler-Elastic模型,避免了产生模糊效果,对辣椒的细节保持较好,也没有损害图像的清晰度。
由图3,CTV模型在处理噪声时产生了明显的马赛克效果,处理后的图像也不够清晰。MTV模型虽对模糊效果的处理比CTV好很多,但在球的表面还是有大量的噪声没有处理干净。TGV和TC模型虽对噪声处理比较彻底,但对球面的光滑度以及对比度保持的还不够好。S-Euler-Elastic模型不仅能够对噪声实现较好的清除效果,而且处理后的图像也没有明显模糊的现象产生,对于球的光滑度和对比度的保持也比其它模型保持的更好。
3.2 定量分析

根据图4,几种模型在趋势上都是先单调下降再趋于稳定的一个状态,但每个模型的递减速度却是不一样的,递减速度反映了模型的收敛速度。可以看出,低阶模型的递减速度明显缓慢。其中,CTV模型到150步左右才开始趋于平稳,MTV模型与TGV模型的迭代收敛速度比较相近,分别为80步左右和70步左右,相比于其他的传统模型TC模型收敛更快一些,大约在50步。因存在Eluer-Elastic规则项,S-Eluer-Elastic模型递减速度是最快的,只要40步便可以稳定。

图4 不同模型的能量变化情况(a)CTV模型;(b)MTV模型;(c)TC模型;(d)TGV模型;(e)本文模型
通过表1对比传统去噪模型和本文提出的新模型的PSNR、SSIM、运算时间与迭代步数可以发现,因为S-Euler-Elastic模型存在高阶的Euler-Elastic规则项,所以运算时间比其他的低阶模型更久。同样存在高阶项的TC模型也存在运算时间过长的问题。相比较于低阶模型CTV与MTV因不含有高阶项所以运算时间会相对较短,但最终得到的PSNR与SSIM值却不是很理想。因为高阶模型中高阶规则项的存在,能够获得更高的SSIM和PSNR值,得到的图像效果更好。虽然运算时间相对比低阶模型较长,但因算法中引入了FFT快速求解,故相比于其他高阶模型运算时间也会较短。但运算效率还是需进一步提高。

表1 不同模型去噪效果的数值对比
4 结论
本文使用Eluer-Elastic作为去除彩色图像乘性噪声模型的规则项,并将其应用于处理几类经典的噪声模型。在计算过程中,以Split Bregman算法为主,通过引入多个辅助变量以及使用FFT快速算法进行求解。本文提出的S-Eluer-Elastic模型对噪声的处理相比于其他传统模型要更好,且PSNR与SSIM指数也相比传统模型提升了许多。经S-Euler-Elastic模型修复后的图像能获得更高的清晰度与对比度,同时避免了边缘模糊效果的产生。由于Euler-Elastic规则项的引入,使计算效率得到了提高。但因S-Euler-Elastic模型涉及到高阶项以及彩色图像耦合的问题,故计算过程比较复杂,运算时间相对较长,还需要在以后的研究中改进完善。

