基于改进深度残差收缩网络的轴承故障诊断
李雪松,李劲华,吕智涵
(青岛大学数据科学与软件工程学院,青岛 266071)
轴承在各种机械设备中占据重要地位,长时间的运行后,会出现一些故障,如滚动体损伤、内圈损伤、外圈损伤等。轴承故障的智能诊断成为机械故障诊断新的发展趋势,通过采集大量的振动数据,使用人工智能技术分析数据,对轴承的故障情况进行诊断。传统的机械故障诊断是先对振动信号预处理,再使用机器学习中的分类器进行故障诊断[1],因此信号处理的好坏直接关系到故障诊断的效果。常用的信号处理的方法有短时傅里叶变换[2]、希尔伯特变换[3]、S变换[4]、小波变换[5]等。支持向量机[6]、逻辑回归[7]、K近邻[8]等传统的机器学习算法对处理后的信号进行特征提取,由于轴承振动信号是非平稳的,机械设备在工作环境中,易受到强噪声的干扰。传统的机器学习分类仅仅是一种浅层的机器学习模型,这种简单的模型限制了故障诊断中的非线性关系的学习,对故障的正确诊断造成了一定的困难[9-10]。深度学习提供了一种“端到端”的学习范式,整个学习流程不需要人为参与。随着深度学习的高速发展,将深度学习技术应用到故障诊断领域中,能有效提高故障诊断的准确率。宫文峰等[11]对CNN增加dropout和全局均值池化的改进方法提高了轴承故障诊断的准确率,熊剑等[12]将深度残差网络与短时傅里叶变换后的时频图相结合,提高了在噪声干扰下故障诊断的准确率,李晓花等[13]提出了基于深度小波去噪自动编码器来增强了特征的学习能力。赵志宏等[14]将密集连接卷积网络应用在了轴承的故障诊断中,把低层次的特征和高层次的特征结合在了一起,提取到了更加有效的特征信息。虽然深度学习在轴承故障诊断中有了广泛的应用,并提高了故障诊断能力,但是在强噪声下,依然会面对特征提取困难,故障诊断正确率不高的问题。为解决强噪声对故障诊断造成的困难,本文将一维轴承振动信号转换成双传感器时频图,并使用多尺度膨胀卷积对深度残差收缩网络进行改进,建立了新的故障诊断模型。
1 小波变换时频图
目前,处理轴承振动信号的方法主要分为时域分析、频域分析和时频域分析[15]。但是轴承的运行环境复杂,而且是非平稳信号,时域分析和频域分析只能提取单一域的信息[16],时频域分析更善于处理振动信号。本文将采用小波时频变换,将一维的振动信号转换成时间和频率关系的小波时频图。
对于任意的L2(R)空间中的函数f(t),连续小波变换为
(1)
其中,ψa,τ(t)由母小波通过伸缩和平移得到
(2)
其中,a代表尺度因子,表示与频率相关的伸缩;τ代表平衡因子;ψa,τ(t)代表小波基函数。
连续小波变换的关键是小波基函数的选择,常见的小波基有Haar小波、Daubechies小波、Morlet小波等[17-19]。由于Morlet小波与轴承故障的特征比较相似,而Cmor小波是Morlet小波的复数形式,自适应能力比较好[20]。所以,本文选择Cmor3-3小波基来进行连续小波变换。
2 深度学习网络
2.1 深度残差网络
普通的卷积神经网络,网络的层数越深结构越复杂,准确率并不一定会上升,有时反而会变低。随着神经网络技术的不断发展,提出了深度残差网络[21],通过引入了跨层连接,可以将原始输入信息直接传递到后面的网络层。解决了深度卷积神经网络难以训练的问题。残差学习结构如图1所示,图中X代表输入数据,F(X)代表经过卷积层后的数据。

图1 残差学习结构图
2.2 深度残差收缩网络
在复杂的轴承工作环境中,往往会有很多噪声干扰,普通的深度残差网络可能无法提取出真正有用的故障特征信息,影响故障诊断的准确率。为解决上述问题,本文提出了深度残差收缩网络用于轴承振动信号的故障检测,即基于注意力机制下的软阈值化来对深度残差网络进行改进,消除与噪声相关的特征。如图2所示,图中bn代表批量标准化,c代表卷积层的通道数。
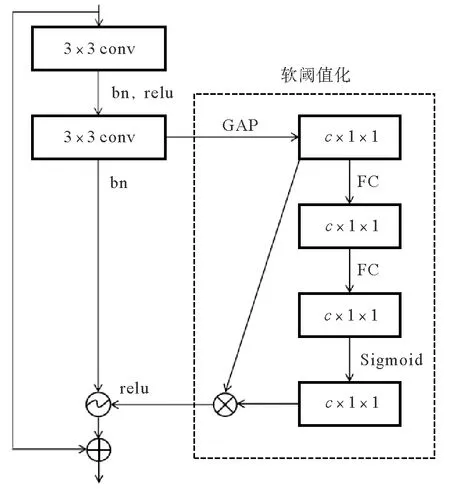
图2 深度残差收缩网络结构
深度残差收缩网络关键思想就是注意力机制和软阈值化的结合。本文使用的注意力机制是SENet,SENet通过一个小型的子网络,学习到一组权重,将权重与各个通道的特征相乘[22],从而将注意力集中在重要的特征上,可以抑制噪声信息。软阈值函数的阈值不是人工设置,而是在网络训练过程中自动设置[23]

(3)
其中,x代表输入的特征值,τ代表网络训练的阈值,y代表输出之后的特征值。通过软阈值化,将特征值的绝对值小于阈值的特征变为0,而绝对值大于阈值的特征向0的方向进行收缩。
深度残差收缩网络的核心网络模块首先经过两次普通卷积,将所有的特征值取绝对值,并将特征值记为X。重要的特征转换成特征值较大的值,经过全局平均池化,再进入到一个小型的全连接网络,最后用Sigmoid函数将输出归一化到0和1之间,记为α。因此深度残差收缩网络训练的阈值就是一个0到1之间的数字与经过全局平均池化后特征值的乘积,也就是α×X。
2.3 多尺度膨胀卷积
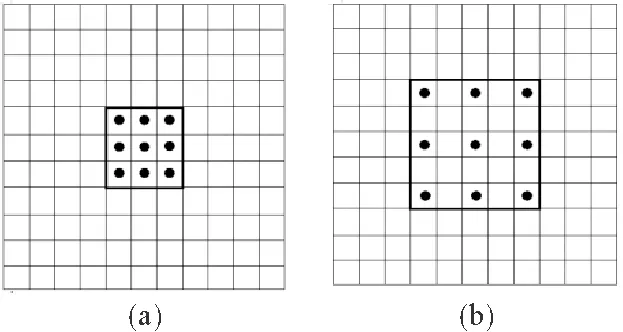
图3 卷积感受野对比(a)普通卷积;(b)扩张率为2的膨胀卷积
深度残差收缩网络会有很多的卷积和池化操作来对特征图进行下采样,这将不断地对时频图的信息造成一些损失,最后导致故障检测的准确率不高。膨胀卷积[24]的思想就是通过对卷积核添加一些空洞,从而扩大模型的感受野,得到更大范围的特征信息。普通卷积和扩张率为2的膨胀卷积如3(a)、(b)所示。膨胀卷积能够代替传统的卷积和池化层的下采样,既有卷积的滤波功能,又有池化层的泛化功能。在不增加模型复杂度的情况下,能够增大卷积核的感受野。
但当在模型中使用多个相同的膨胀卷积后,会发现感受野中依然存在很多空洞问题,这将丢失数据之间的连续性,尤其对轴承的故障检测十分不利。膨胀率越大,采样后的数据就越稀疏,产生网格现象,使参数学习更加困难[25]。同时融合多个膨胀卷积,可以有效抑制膨胀卷积的网格效应。于是本文将扩张率为1,2,3的膨胀卷积,采用加和平均的方式进行特征融合,多尺度膨胀卷积结构如图4所示。通过多尺度的融合,在7×7的区域内有25个采样点,可以很好的解决膨胀卷积导致的数据稀疏的问题。
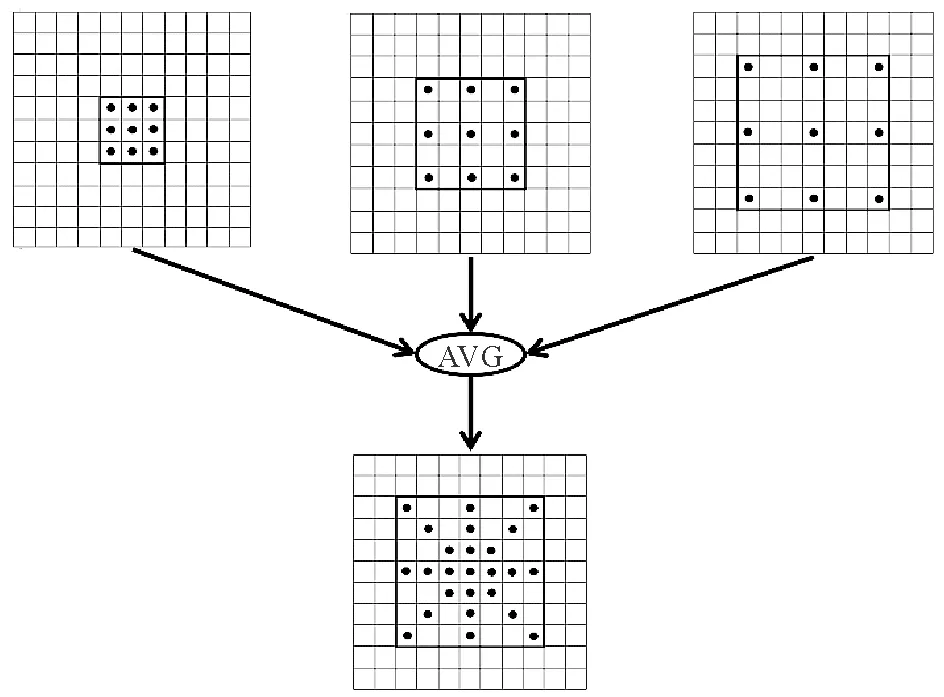
图4 多尺度膨胀卷积融合
3 实验验证
3.1 故障诊断流程
现用实验验证建立的多尺度膨胀卷积和深度残差收缩网络结合的轴承故障诊断模型的准确率。模型输入的数据是通过连续小波变换后的小波灰度图,图像大小为64×64×1。模型以resnet18为基础框架,并在每个残差块中添加了注意力机制下的软阈值化,经过多次测试,把其中的两个普通卷积由多尺度膨胀卷积代替效果最好,改进后可以提高模型的抗噪性。
为了提高故障诊断的抗噪性,使用多个传感器来采集振动信号,并将其合并后转换成时频图。实验采用西储大学轴承数据[26]。
Step1首先在机械设备的驱动端和风扇端分别安装传感器,用来采集轴承的振动信号。采用西储大学轴承故障数据库[26]中驱动端轴承6 250的故障数据,实验设备如图5所示,采样频率为12 kHZ,轴承的转速为1 797 r/min,1 772 r/min,1 750 r/min,1 730 r/min,选取10种故障类型,即正常状态,损伤包括φ0.007英寸、φ0.014英寸、φ0.021英寸的钢球、内圈和外圈单点故障。

图5 滚动轴承实验设备
Step2由于西储大学轴承的运行环境比较理想,所以为了仿真轴承复杂的运行环境,给振动信号加入-2dB,-3dB的高斯噪声。以1 024个采样点为一个样本,分别将驱动端和风扇端的振动信号通过连续小波变换转换成时频图,合并成64×64×1的小波时频灰度图。以φ0.014英寸的滚动体故障在驱动端的信号为例,添加噪声之后的结果如图6。
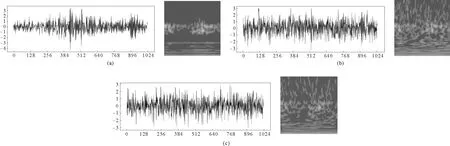
图6 轴承振动信号及其对应的小波时频图(a)原始信号和小波时频图;(b)添加-2dB之后的信号和小波时频图;(c)添加-3dB之后的信号和小波时频图
Step3将合并后的小波时频灰度图划分成训练集和测试集,每种故障类型选取470个样本,正常状态选取870个样本,具体数据集分布见表1。

表1 数据集分布 单位:个
Step4将训练好的模型对测试集进行测试,通过混淆矩阵查看各个故障的诊断情况。
由于工厂机械的运行背景噪声的干扰,以及有些故障的振动信号相似度较高,难以区分,仅仅通过一个传感器来进行故障诊断的准确率不高,因此使用双传感器进行信息的采集,将从风扇端和驱动端采集到的振动信号合并后再转换成时频图,最终产生的时频图如图7所示。

图7 合并之后的时频图
3.2 训练模型
定义每个训练batch包括32个样本,一共训练40个epoch,Adam[27]作为优化器,激活函数为Relu[28]。在这里对交叉熵损失函数增加每个故障类别的权重,改进成加权交叉熵损失函数。普通交叉熵损失函数
(4)
其中,m是一个batch的样本数;是代表轴承故障数据集的故障类别总数;pij代表第i个样本是不是属于j样本。qij是第i个样本经过softmax函数之后输出0到1之间的值。加权交叉熵损失函数
(5)
其中,wij是i个样本的对应类别j的权重。这里将故障状态的权重设置为4,正常状态的权重依然为1。在噪声的影响下,模型最终得到的训练准确率和训练误差的变化过程如图8所示。可知,网络训练在第20次迭代时趋于稳定,具有较好的收敛性。
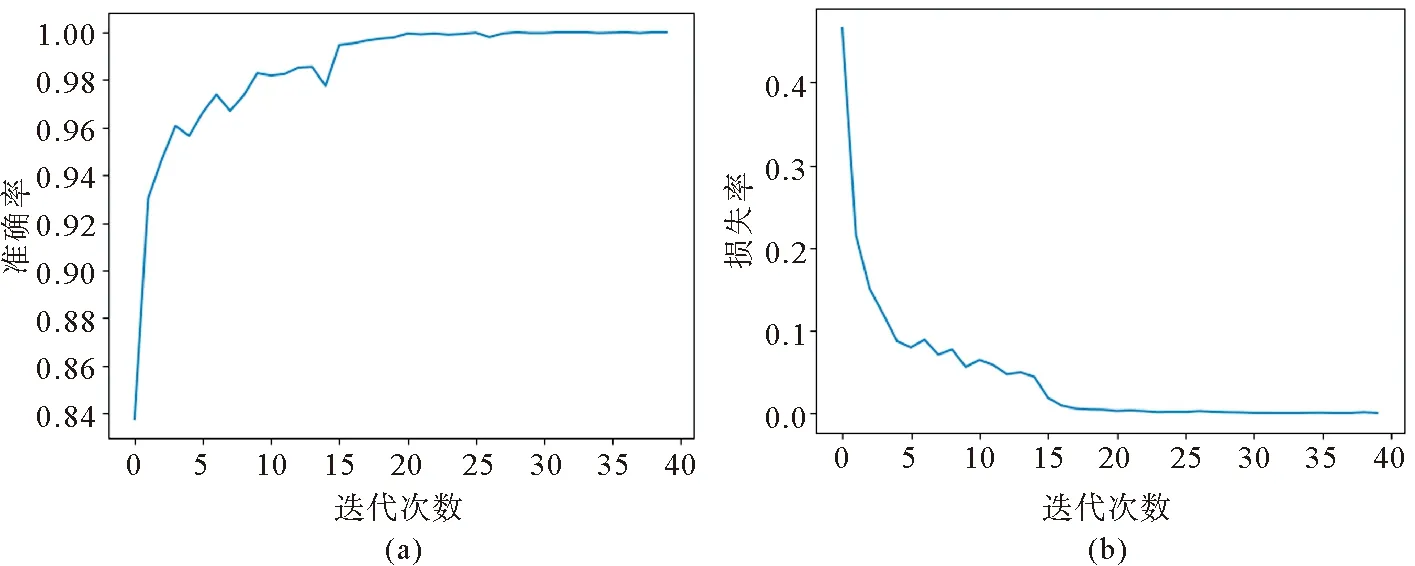
图8 训练过程曲线(a)-2dB下的准确率;(b)-2dB下的损失率
3.3 对比实验
为了证明改进后的深度残差收缩网络与双传感器结合的有效性,本文处理一维振动信号的SVM,与擅长处理二维图片的LeNet-5、ResNet、DRSN进行对比,分别实验10次,平均准确率见表2。可知,机器学习算法的准确率较低,而深度学习算法的准确率都在90%以上。本文方法在两种噪声背景下都取得99%以上的准确率,相对于传统的机器学习方法的准确率分别高出12.8%和16.8%,相对于目前应用比较好的ResNet的准确率高出3.1%和4.4%,具有明显的优势。

表2 实验结果对比
为研究本文模型的故障诊断结果,绘制了混淆矩阵。结果如图9所示。可知,F1故障和F6故障,F3故障和F6故障易于混淆,振动信号较为相似,在噪声背景的情况下,依然无法提取出有效信息,这是下一步研究的重点。而其他故障的特征比较明显,易于区分。
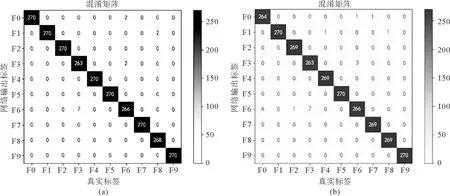
图9 混淆矩阵(a)-2dB下的混淆矩阵;(b)-3dB下的混淆矩阵
4 结论
本文提出了一种基于改进的深度残差收缩网络与双传感器时频图相结合的轴承智能诊断方法,对受到噪声干扰的轴承故障信号进行分析。深度残差收缩网络中自注意机制下的软阈值化,可以很好的增强有效信息,减弱无效的噪声干扰信息,Resnet、LetNet有着更好的抗噪性,适用于滚动轴承的故障诊断。多尺度膨胀卷积的引入可以更好的解决单一连续膨胀卷积会产生的网格效应,并且可以增大卷积核对时频图的感受野,对提高轴承故障诊断的准确率有着很好的帮助。双传感器时频图可以很好的解决单一传感器时频图准确率不高的问题,加权交叉熵在一定程度上可以抑制轴承故障数据不平衡的问题。

