基于改进小波神经网络的集装箱船纵摇角度预测
张 婷,王志明,王培良
基于改进小波神经网络的集装箱船纵摇角度预测
张 婷1,2,王志明2,王培良2
(1. 山东交通职业学院航海学院,山东 潍坊 261206;2. 上海海事大学商船学院 / 航运仿真技术教育部工程研究中心,上海 201306)
【】针对在航集装箱船舶纵摇角度预测问题,探索一种基于改进小波神经网络算法,提升其预测能力。在分析船舶纵摇角度原始数据基础上,引入傅立叶变换,分析计算数据的周期性,确定神经网络拓扑结构,然后将神经网络输入层和隐含层的连接权值融合到隐含层计算值中,使算法得到优化。【】优化后小波神经网络能较准确预测船舶纵摇角度值,均方误差(MSE)值为0.067 6,平均绝对百分误差(MAPE)值为4.241 2,相比优化前分别提升25%和21%,具有更好的预测效果。
小波神经网络;船舶纵摇预测;集装箱船;隐含层优化;傅立叶变换
集装箱船航行环境较为多变和复杂,在风、浪、流等作用下,其运动可能出现六自由度方向变化[1]。当船舶正常航行运动状态被打破,船舶六自由度方向运动均会产生重大变化,尤其船舶摇荡加剧时,严重威胁船舶航行安全。因此,对船舶运动状态进行准确预测,可有效提高船舶航行安全性,其意义重大[2-3]。当前,船舶纵摇运动预测方法主要有时间序列分析法、卡尔曼滤波法、艏前波法以及人工神经网络法等[4-5]。其中,神经网络法具有学习能力强,适应性高等优点,在非线性研究中具有较高的应用价值[6]。小波神经网络属于反馈型神经网络,但并未使用传统的Sigmoid函数,而是使用小波基函数作为转换函数[7]。在复杂系统建模中,小波神经网络具有良好的局部时间频率特性表现,因而受到越来越多的关注和研究。孙珊珊[8]基于小波神经网络,结合成型滤波器对船舶运动的噪声信号进行抑制和过滤,研究预测对船舶的运动受扰力;章文俊等[9]基于小波神经网络并结合MMG模型研究预测船舶运动;Zhang等[10]提出时滞小波神经网络,研究预测船舶运动;Yin等[11]基于小波变换和RBF神经网络,研究预测船舶横摇运动。在利用小波神经网络进行预测研究的报道中,尚未见对小波神经网络的隐含层进行优化分析。因此,本研究提出基于隐含层输出优化的方法构建小波神经网络,同时,引入学习速率以修正网络参数,提升网络的收敛速度,避免陷入局部极值,以期利用优化后的小波神经网络提升船舶纵摇运动预测能力。
1 方法
1.1 小波神经网络结构
小波神经网络作为多层前馈神经网络,其特点为信号前向传递、误差反向传播。在前向传递过程中,信号从输入层进入网络,经隐含层处理后到达输出层;如果输出层的输出值无法满足期望,则依据预测误差调整网络的权值和阈值,从而使神经网络的输出值不断接近期望值。小波神经网络拓扑结构见图1。

图1 小波神经网络拓朴结构
图1中,1,2,…,X是小波神经网络的输入值,1,2,…,Y是小波神经网络的预测值,和分别为输入层和输出层的节点数量,ω和ω分别为输入层、隐含层、输出层之间的连接权值[12]。
1.2 网络输出计算
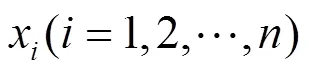
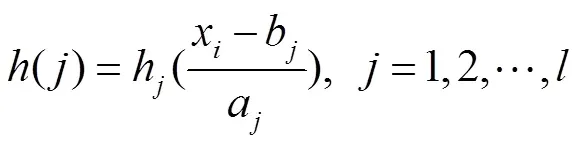
其中,()为隐含层第个节点的输出值,为隐含层节点数量,b为小波基函数h的平移因子,a为小波基函数h的伸缩因子。本研究采用Morlet母小波基函数,其计算公式如下:
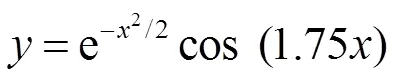
其中,、分别代表自变量和因变量。
因此,小波神经网络的输出值计算公式如下:
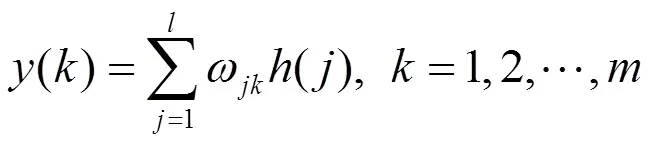
1.3 隐含层输出优化
传统神经网络隐含层的计算值虽均经小波函数变换,但由于受输入层数据的影响,数值之间波动较大,且计算方法较为单一,无法满足复杂环境下的工程应用。
本研究对隐含层输出计算的优化主要是在传统方法基础上,结合输入层和隐含层之间量化后的连接权值,达到弱化单一输入数据的目标,其计算公式如下:
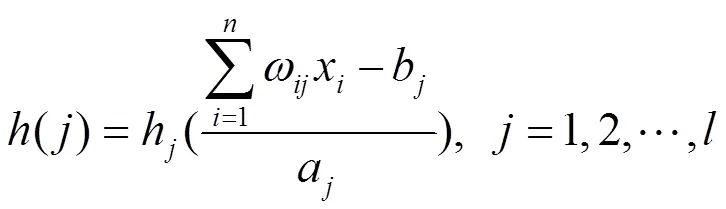
1.4 网络参数修正
修正小波神经网络权值和基函数参数的目的,是减小网络输出值与期望值之间的误差,本研究采用梯度下降法,同时引进学习速率法以提升神经网络的收敛速度[13]。
小波神经网络权值修正方式有两种:一是按输入样本逐次修正,二是全部样本输入后再修正。本研究采用逐次修正方式。预测值与期望值之间的误差,其计算公式如下:
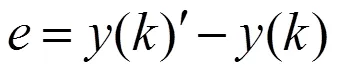
根据预测误差修正网络权值和参数,同时为加快算法收敛速度,避免算法陷入局部最小值,引入学习速率,计算公式如下:
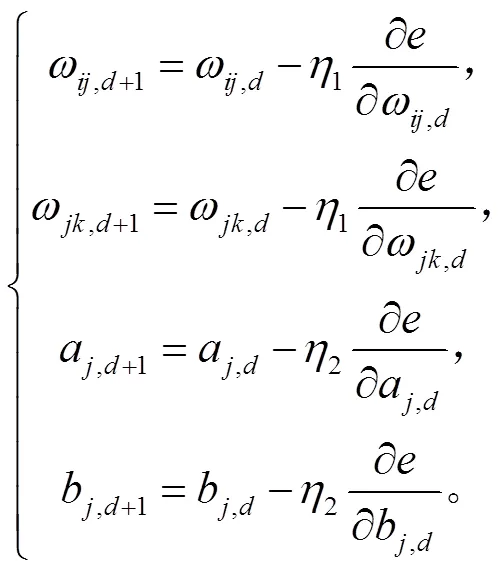
其中,为训练次数,1、2为网络学习速率。
1.5 预测结果度量
为量化小波神经网络优化前后的预测结果,并与其他算法模型进行对比,本研究使用均方误差(MSE)和平均绝对百分误差(MAPE)进行预测误差分析,计算公式如下:
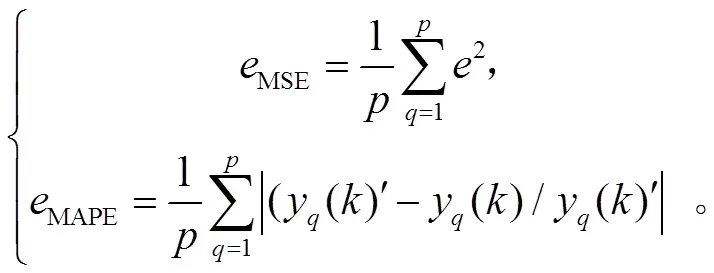
其中,为预测数据数量,一般认定MAPE值小于10时,预测效果良好[14]。
1.6 算法流程
综合1.1—1.5节,使用小波神经网络进行预测的算法流程见图2。
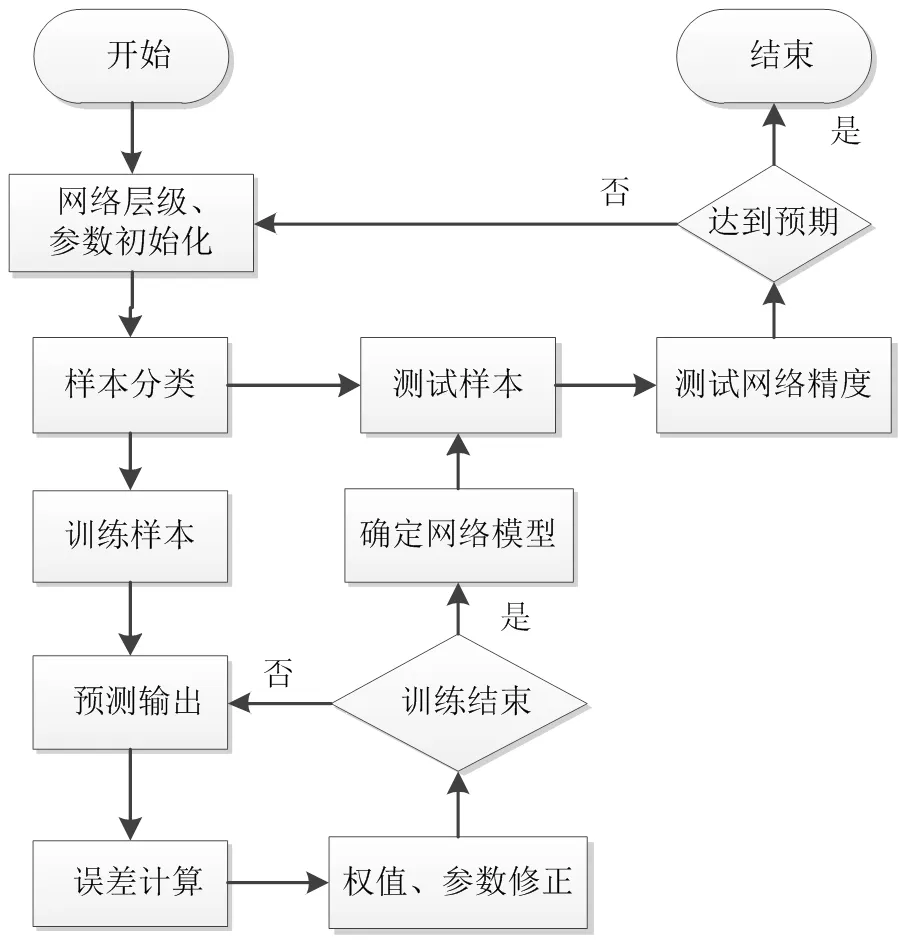
图2 算法流程
2 数据处理
为验证小波神经网络的预测效果,本研究选取某集装箱船纵摇角度数据作为算例。在船艏位置V1安置角度传感器(图3),以获取船舶的纵摇角度。
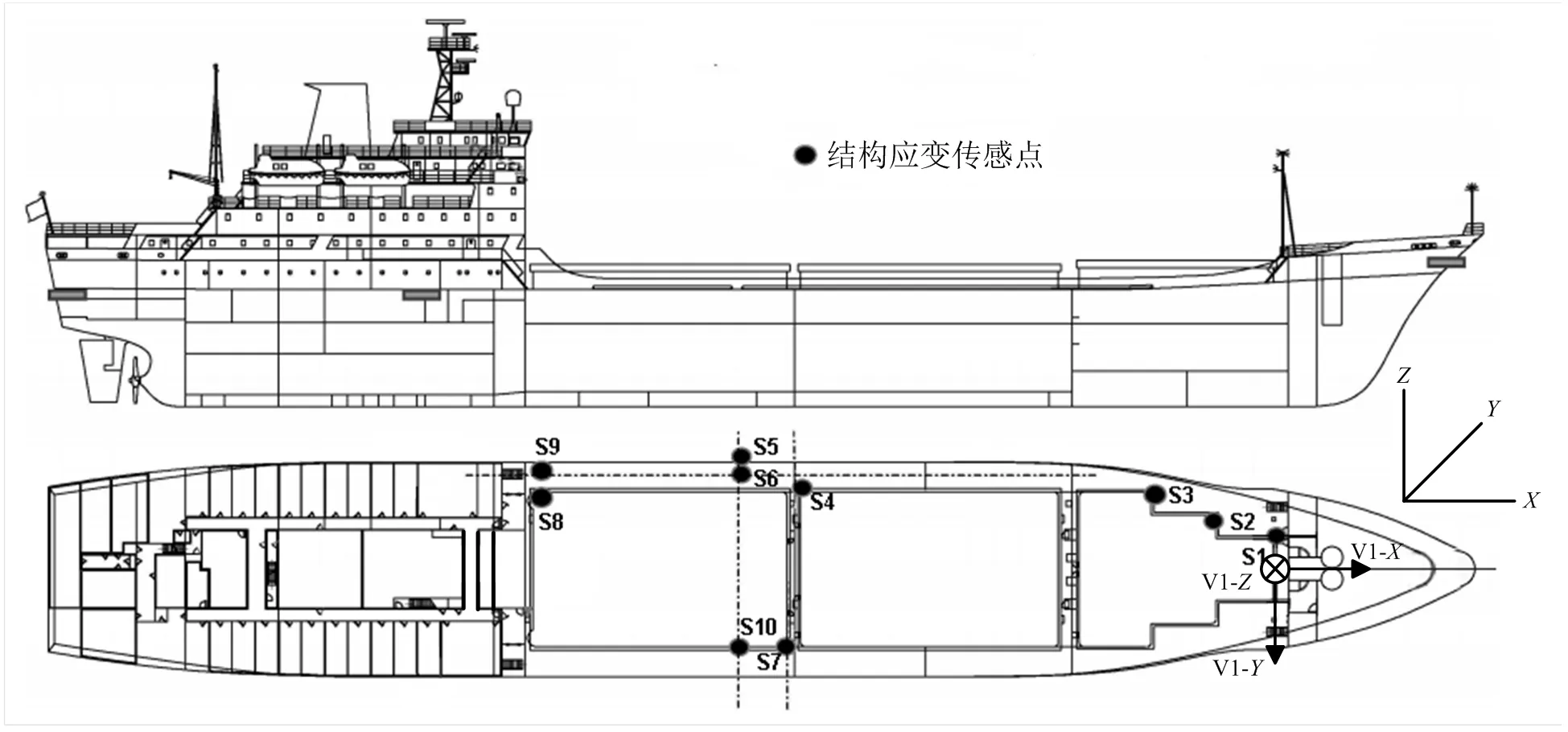
图3 船舶传感器测点布置
本研究以船载传感器某1 h内采集的2400组数据为样本,同时为避免噪声干扰及研究时间度量需要,以每15 s采集的数据均值作为当次摇摆角度值(图4)。
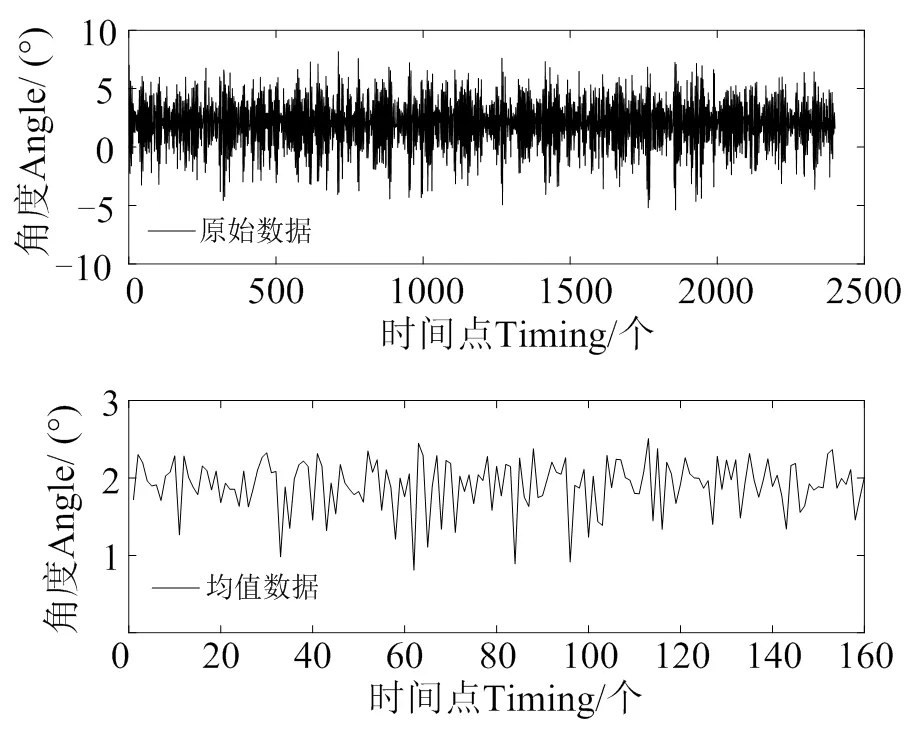
图4 船舶纵摇角度序列
反馈式小波神经网络具有输入延迟性,因此,根据采样数据时间性质,以前45 min的摇摆角度数据作为小波神经网络的训练数据,后15 min的均值数据作为神经网络的预测数据进行模型验证。
纵摇角度值呈现出周期特性,使用傅立叶变换进行分析(图5)。
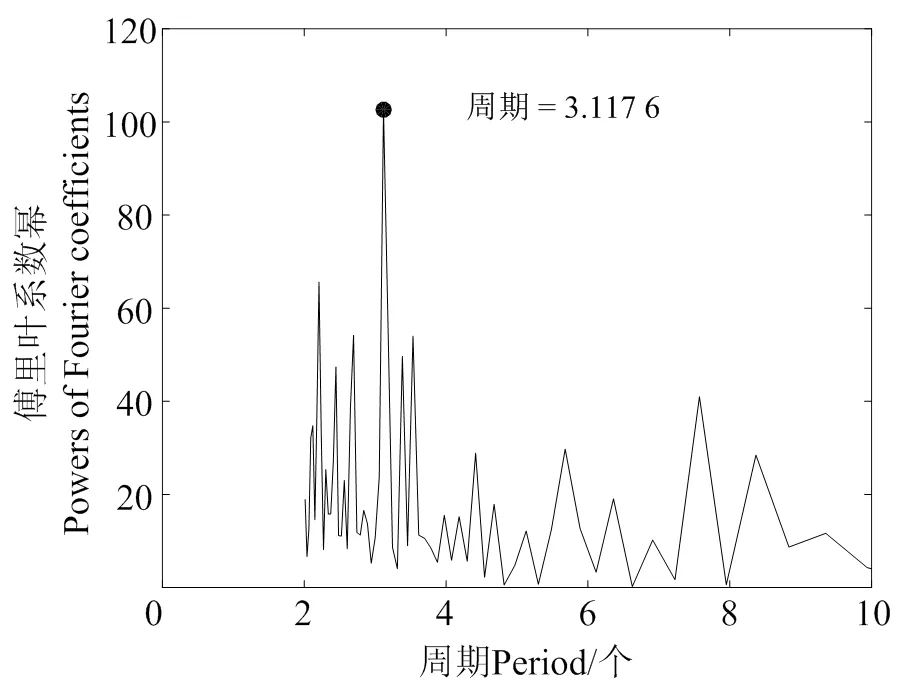
图5 周期性测试分析
由图5可知,纵摇角度值周期约为3。因此,小波神经网络拓扑结构为3-6-1,即输入节点数为3,输出层节点数为1,隐含层节点数为6。神经网络权值采用随机数据,其他初始化参数见表1。

表1 小波神经网络初始化参数
3 结果与分析
3.1 网络训练结果
在以训练数据为基础进行神经网络迭代训练过程中,优化前后的神经网络预测误差变化趋势见图6。由图6可见,小波神经网络的预测误差随着迭代次数增加而逐渐减小,表明误差反馈给神经网络的调节效果良好,能有效修正神经网络。优化后的小波神经网络在初始误差值、误差下降速率以及误差下降趋势等方面均获得提升。优化后的神经网络随着迭代次数的增加,误差依旧持续性下降,表明网络的收敛性良好,可进一步提升预测效果。
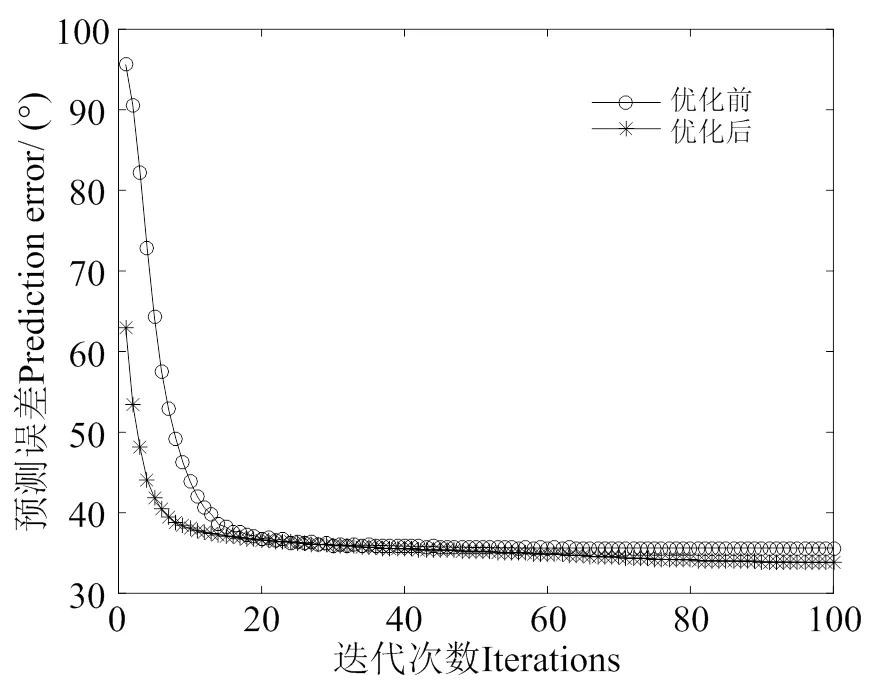
图6 神经网络迭代过程
3.2 网络预测结果
用3.1节训练好的小波神经网络对船舶纵摇角度值进行预测,预测效果对比见图7。

A, 预测效果对比; B, 网络优化前后对比
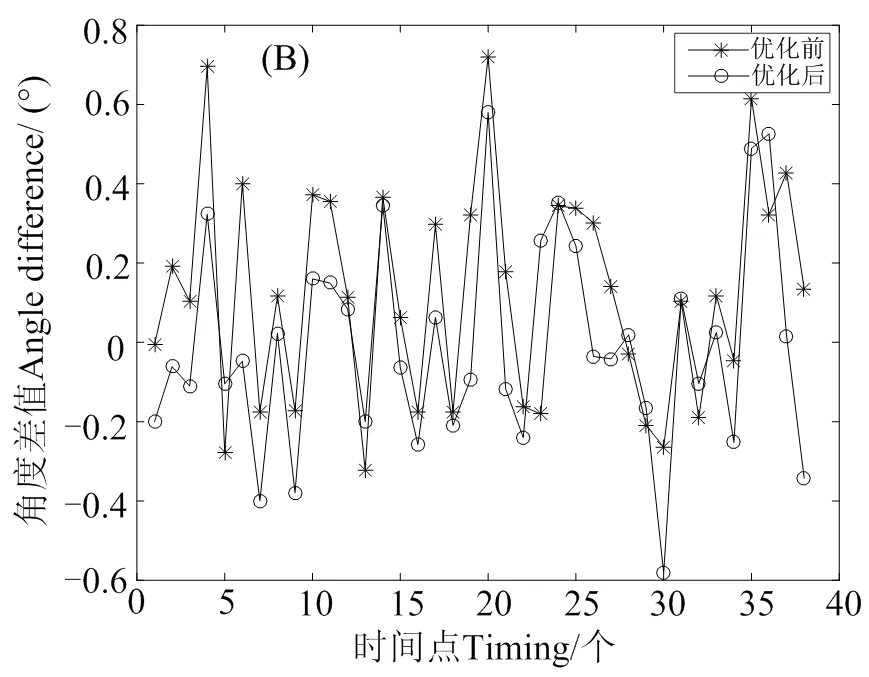
图7(续)
Fig. 7(Continued)
由图7可知,优化后小波神经网络对船舶纵摇角度值的预测值接近与实际期望值,且对角度值变化趋势的预测较为准确。网络优化前后的MAPE值分别为5.368 8和4.241 2,优化效果提升21%,表明优化网络后的预测精度更高,预测效果更佳。
使用MSE值表征不同方法的预测精度(表2),可见优化后小波神经网络MSE值比优化前变小,优化效果提升25%。本研究方法在部分优化网络参数的情况下对船舶纵摇角度进行预测,其MSE值已接近ARIMA(1,1,1)模型[5]预测结果,说明本研究方法能较好预测船舶纵摇角度值。对网络参数进行整体优化,预计将可获得更好的预测精度。

表2 模型预测精度
4 讨论
为克服传统小波神经网络隐含层值计算方法单一且波动较大的缺陷,本研究量化输入层和隐含层之间的连接权值,并将其融入到隐含层的计算方法中,从而使单一数据目标得到弱化;同时结合傅立叶变换求解数据的周期性,确定神经网络拓扑结构,为小波神经网络的优化提供新的借鉴思路。但本研究方法所用各类参数的初始值大多采用专家经验法,数值的选择并非为最优值,预测结果仍有提升空间。后续,本研究方法将结合参数优化算法(如PSO算法、GA算法等)进行更进一步的优化研究。
5 结论
本研究采用傅立叶变换求解船舶纵摇角度数据的周期性,确定小波神经网络的拓扑结构,将神经网络输入层和隐含层的连接权值融合到隐含层计算值中,以增强算法预测能力。同时,本研究以MSE和MAPE值作为评价指标,对比不同预测方法的预测效果。结果表明,优化后小波神经网络MSE和MAPE值比优化前分别提升25%、21%,具有更好的预测效果。优化后小波神经网络能较准确预测船舶纵摇运动,可为实际工程应用提供有益参考。
[1] 张腾, 任俊生, 范小晴, 等. 基于多系数保角变换法的船舶垂荡纵摇运动仿真[J]. 上海海事大学学报, 2019, 40(3): 51-56.
[2] 李远芳, 李俊彪, 张莉. 海洋环境预测数据在船舶航行控制中的应用[J]. 舰船科学技术, 2020, 42(16): 37-39.
[3] 徐东星. 改进天牛群搜索算法及其在船舶纵摇运动预测中的应用[J]. 广东海洋大学学报, 2021, 41(3): 113-122.
[4] 张春娜. 基于经验模态分解的舰船运动姿态预测模型研究[J]. 舰船科学技术, 2021, 43(2): 22-24.
[5] 王培良, 张婷, 肖英杰. 基于改进PSO-ARIMA模型的船舶纵摇角度预测[J]. 上海海事大学学报, 2021, 42(1): 39-43.
[6] 彭秀艳, 张彪. 基于EMD-PSO-LSTM组合模型的船舶运动姿态预测[J]. 中国惯性技术学报, 2019, 27(4): 421-426.
[7] 张蓓, 姚亚锋, 季京晨. 基于小波神经网络的地铁基坑地表沉降随机预测[J]. 铁道科学与工程学报, 2021, 18(11): 2899-2906.
[8] 孙珊珊. 小波神经网络舰船运动受扰力预测模型[J]. 舰船科学技术, 2021, 43(8): 4-6.
[9] 章文俊, 刘正江. 基于小波神经网络的船舶运动预报[J]. 大连海事大学学报, 2013, 39(2): 25-28.
[10] ZHANG W J, LIU Z J. Real-time ship motion prediction based on time delay wavelet neural network[J]. Journal of Applied Mathematics, 2014, 2014: 176297.
[11] YIN J C, PERAKIS A N, WANG N. A real-time ship roll motion prediction using wavelet transform and variable RBF network[J]. Ocean Engineering, 2018, 160: 10-19.
[12] 于仁海, 曹春燕, 张闯, 等. 基于递归模糊小波神经网络的INS-GNSS组合导航算法[J]. 上海海事大学学报, 2021, 42(2): 8-14.
[13] 宋瑞蓉, 王斌君, 仝鑫, 等. 基于改进果蝇的混合小波神经网络交通流预测[J]. 科学技术与工程, 2021, 21(15): 6394-6401.
[14] 张良均, 杨坦, 肖刚, 等. MATLAB数据分析与挖掘实战[M]. 北京: 机械工业出版社, 2015: 91-92.
Pitch Angle Prediction of Container Ship Based on Improved Wavelet Neural Network
ZHANG Ting1,2, WANG Zhi-ming2, WANG Pei-liang2
(1.,,261206,; 2.,/,201306,)
【】To resolve the problem of pitch angle prediction of container ships in navigation, an improved wavelet neural network method was proposed.【】On the basis of analyzing the original data of the pitch angle of the ship, the Fourier transform is introduced firstly to analyze the periodicity of the calculation data. The topology of the neural network is determined. And then the connection weights between the input layer and the hidden layer of the neural network are calculated to enhance the algorithm's prediction ability. 【】The simulation results show that the optimized wavelet neural network can more accurately predict the pitch angle value of the ship. The MSE value is 0.067 6, and the MAPE value is 4.241 2,25% and 21% respectively higher than those before optimization.The optimized wavelet neural network has certain advantages in practical engineering applications.
wavelet neural network; ship pitch prediction; container ship; hidden layer optimization; Fourier transform
张婷,王志明,王培良. 基于改进小波神经网络的集装箱船纵摇角度预测[J]. 广东海洋大学学报,2022,42(3):117-121.
U661.42
A
1673-9159(2022)03-0117-05
10.3969/j.issn.1673-9159.2022.03.015
2022-01-21
国家青年自然科学基金(51909155);潍坊市软科学研究计划项目(2021RKX125)
张婷(1987―),女,硕士,研究方向为航海技术、智能交通。E-mail:titi-507@163.com
王培良(1987―),男,博士,讲师,研究方向为智能交通。E-mail:gfy5216@126.com

