基于非对称荷载作用下的基坑变形特性研究*

赵 平

(铜陵学院建筑工程学院，安徽 铜陵 244000)

引言

偏压基坑是指基坑两侧存在相差较大荷载而处于不对称受力状态下的基坑，不同原因引起的偏压问题十分常见，偏压基坑变形性状呈现出不同于普通基坑的特点，主要表现在基坑两侧不平衡堆载、不同挖深以及基坑周边不同土质等方面，按常规方法设计存在一定安全隐患[1-4].已有的基坑实测结果表明，临近建(构)筑物的超载会对基坑产生不利影响，严重时还可能引起基坑破坏[5]，此类基坑的研究日益被学者所关注[6,7].现场监测方面，刘波等[8]通过现场监测资料分析了该深基坑在偏压作用下围护桩的桩体深层水平位移变化规律；方焘等[9]对邻近有地铁车站形成的两侧土体宽度非对称的基坑开挖进行数值模拟，并与现场监测数据进行对比；王鹏[10]通过采用现场实测的方法对不同偏压荷载下的深基坑受力与变形规律进行了研究.理论分析方面，吴波等[11]采用模糊层次分析法建立了地铁深基坑非对称施工的评估模型；周勇等[12]结合土体与桩共同变形的挠曲线方程，推导出支护桩的水平位移公式；范晓真等[13]引入考虑位移的非极限状态土压力理论，对作用于支护结构上的土压力进行了修正.数值模拟方面，杨琴等[14]采用MIDAS GTS软件进行三维有限元计算，研究了基坑两侧地面标高不等、两侧围护结构刚度不等对基坑开挖变形的影响；陈军等[15]在Plaxis软件中采用考虑土体效应变特性的HS本构模型，研究了多级支护非对称受荷基坑的变形特性；孙武斌[16]采用FLAC3D建立三维数值计算模型对地铁车站偏压基坑围护结构变形影响因素开展了研究.

综上所述，当前关于偏压基坑开挖影响日益被学者所关注，并取得了较丰富的成果.但目前类似研究中，大部分学者研究的对象为地铁车站深基坑工程，但对管廊基坑工程在非对称荷载条件下开挖变形特性研究甚少.此外，由于综合管廊项目大多位于城市人口密集区，建设过程中不可避免地会对邻近建(构)筑物产生影响[17,18].本文在上述研究的基础上，以合肥市某管廊基坑工程开挖工程为工程背景，基于修正摩尔库仑本构模型，采用MIDAS/GTS对基坑开挖及支护全过程进行数值模拟，研究了非对称荷载作用下深基坑开挖引起的地下连续墙水平变形规律，模型计算结果与实测数据吻合良好，在此基础上研究了荷载距离D的改变对内支撑轴力及坑外地表沉降的影响.得到的结论可为后续类似工程设计及更深入的理论研究提供参考.

1 工程概况

本文研究对象为合肥市某综合管廊(明挖段)基坑工程.基坑截面示意图见图1.基坑右侧作为施工场地，距离坑外D=5 m处堆放有钢筋等各种施工材料，经施工单位测算，施工材料将产生17 kPa的地面超载，超载作用范围L=7 m，因此基坑开挖在非对称荷载作用下进行.此外，基坑长度为826 m，宽度为8 m，开挖深度为7 m，为长条形基坑.基坑的支护结构由地下连续墙和两道内支撑组成，其中：内支撑均为圆管型钢支撑，截面外径为609 mm、截面厚度为16 mm，内支撑具体位置布置在距离地表以下1 m、4 m处，内支撑水平间距均为5 m.地下连续墙为钢筋混凝土墙，高度为14 m，其中嵌入土体深度为7 m，厚度为800 mm.此外，地下连续墙采用C30混凝土，弹性模量为3 100 000 kN·m-2，泊松比为0.22，重度为29 kN·m-3；钢支撑弹性模量为218 000 000 kN·m-2，泊松比为0.32，重度为77 kN·m-3.基坑共分3次开挖，开挖深度依次为：1 m、3 m及3 m.根据岩土工程勘察报告，简化后的土层为5层，参见基坑典型截面示意图(图1).土体力学参数如表1所示.

图1 基坑典型截面示意图

表1 计算模型土层力学参数

2 建模与计算

2.1 MIDAS/GTS NX软件在基坑工程中的运用

MIDAS/GTS NX软件是一个专门用于岩土工程问题中变形和稳定性分析的计算软件，在基坑工程的数值模拟中也被广泛应用[9,14].张艳书等[19]、刘雪珠等[20]、麻凤海等[21]、张振昌等[22]均采用MIDAS/GTS软件对基坑开挖过程产生的相关影响开展了研究，内容包括：软土层对地铁狭长深基坑地表沉降影响的研究、坑底加固置换率对杭州地铁湘湖站深基坑安全的影响分析、基坑施工的全过程进行全面动态模拟，以及隧道区间典型截面开挖、支护及浇筑等全过程进行有限元模拟分析，并与现场沉降监测数据进行了对比.研究结果表明MIDAS/GTS NX软件在深基坑工程中的运用广泛，并取得了较好的模拟效果.本次研究选用MIDAS/GTS NX软件进行数值模拟.

2.2 基本假定

由于施工过程和现场工程条件比较复杂，为了便于计算研究，数值模型设计对实际情况进行一定简化，本研究基本假设如下：①各层土体连续且均匀分布；②不考虑地下水对围护结构变形的影响；③地下连续墙和内支撑均为弹性体；④同一种材料为均质、各向同性.

2.3 建立模型

由于基坑长度为826 m、宽度为8 m，呈窄长条形，基坑长度约为宽度的103倍，故对于非坑角区域，可以简化为平面应变问题进行分析[21，22].使用有限元计算软件MIDAS/GTS NX建立二维基坑模型.根据圣维南原理，考虑工程实际情况，本文建立的整体二维模型宽(x)、高(y)分别为：48 m、30 m，远大于预计基坑开挖影响范围.模型坐标系按照图2中所示：X轴正方向指向基坑宽，Y轴正方向竖直向上.模型采用标准边界条件，模型左右边界仅允许发生竖向位移，顶部为自由边界允许发生横向和竖向位移，底部为固定约束.此外，地下连续墙与土体在强度和刚度上存在较大差异，在外力作用下其界面有可能产生相对滑移或脱离[23].为此，为了更好地开展数值模拟，在地下连续墙与土体之间设置接触面单元.本次研究采用软件自带的库仑摩擦界面单元体现地下连续墙与土体之间接触面的特性.当表面发生接触时，在接触面之间传递切向力和法向力.模型中法向刚度模量和剪切刚度模量取值分别为：800 000 kN/m3和8 000 kN/m3，不考虑非线性接触.由于基坑周围土体的变形响应具有明显的小应变特性，数值模型中土体采用修正摩尔库仑本构关系.模型中土体为考虑平面应变的2D面单元，地下连续墙、基坑内支撑均采用1D梁单元.整体二维模型网格划分情况如图2所示.数值模型共计2 435个单元，2 502个节点.

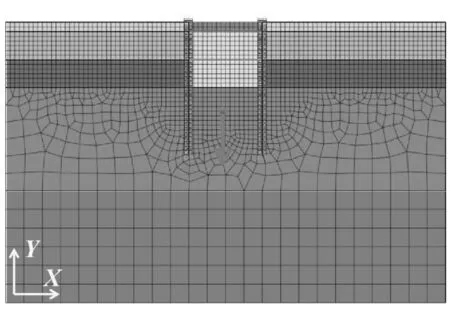
图2 二维有限元模型

2.4 模拟施工

数值模拟中基坑的开挖和支护分别通过软件中的命令钝化和激活来控制，数值模拟的基坑开挖过程与实际现场基坑开挖过程保持一致，施工工况具体内容为：①进行初始地应力分析，位移清零；②地下连续墙施工；③开挖1，基坑开挖1m；④开挖2，基坑开挖3 m，施作第一道支撑；⑤开挖3，基坑开挖3 m，施作第二道支撑.

3 数值模拟结果与现场实测对比分析

数值模拟方法具有可以动态模拟基坑开挖与支护施工过程等优点，且现场监测可以对施工过程实施监控和动态控制，对有效确保基坑开挖施工过程和基坑周围既有建筑的安全有一定的促进作用[24].图3 为工况5下左侧地下连续墙水平位移模拟值与监测值对比曲线图，图4 为工况5下右侧地下连续墙水平位移模拟值与监测值对比曲线图，由图3和图4对比发现，基坑开挖完成时，无论是左侧地下连续墙，还是右侧地下连续墙都呈现出朝向基坑内部的“凸鼓状”变形规律，此结论与高亿文等[5]在研究超载影响下围护结构非对称基坑的受力及变形特性分析得出的结论相吻合.数值模拟与现场监测值接近，且最大水平位移均发生在地下连续墙深度约为6 m的位置.此外，还可以得出，偏压作用下，基坑两侧地下连续墙水平变形规律与对称荷载条件下存在很大差异，基坑同一断面内有荷载一侧的水平变形均大于无荷载一侧.具体来看，图3中，最大水平位移分别约为6.2 mm、7.9 mm，变形规律相似，最大值较接近.值得注意的是，开挖完成时，在地下连续墙顶部出现了朝向基坑外侧的变形，水平位移模拟值与监测值分别约为2 mm、3.2 mm，这可能是由于该基坑受到非对称的地表超载影响造成的.图4中，最大水平位移分别约为8.5 mm、9.8 mm，变形规律相似，最大值较接近.模拟结果中，左侧地下连续墙最大水平位移比右侧地下连续墙最大水平位移小约2.3 mm，这可能是由于偏压荷载在增加偏压侧地下连续墙水平位移的同时抑制非偏压侧的地下连续墙水平位移.综上所述，数值模拟与现场监测值接近，变形规律类似，由此说明此次基坑开挖及支护结构设计合理，验证了数值模拟参数选取的可行性，并得出了基坑开挖完成时地下连续墙水平变形规律，可以在此基础上开展基坑荷载距离D改变时内支撑轴力和地表沉降的相关分析.

图3 工况5下左侧地下连续墙水平位移模拟值与监测值

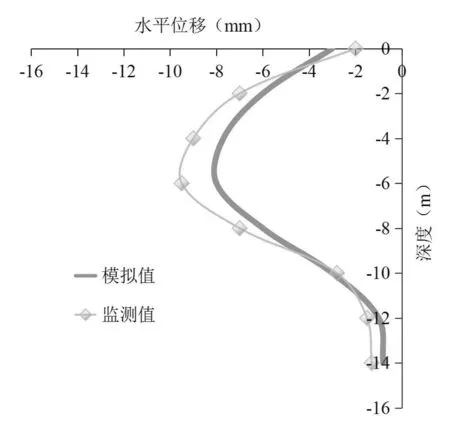
图4 工况5下右侧地下连续墙水平位移模拟值与监测值

4 基坑右侧荷载距离不同情况的计算与分析

非对称荷载作用下的基坑开挖工程中引起的支护结构内力以及地表竖向变形与基坑开挖过程中很多因素有关，学者高亿文[5]的研究成果显示，非对称荷载作用下的基坑开挖工程中引起的支护结构内力以及地表竖向变形的因素主要有以下几类：超载的位置、超载的大小、内支撑的设计参数以及超载的范围等.考虑到内支撑轴力是评判基坑开挖过程中支护结构稳定性的重要指标之一，且地表竖向变形对基坑周围环境会产生直接影响.本次研究只讨论超载距离地下连续墙距离D的改变而引起的内支撑轴力以及地表竖向变形影响，D的取值分别为：5 m、6 m、7 m、8 m、9 m以及10 m.分别改变超载距离地下连续墙距离D，其他参数保持不变，运用改变后的参数，分别建立二维数值模型，通过数值模拟结果研究该参数改变对支撑轴力和地表竖向位移的影响.

4.1 支撑轴力分析

图5 为超载距离地下连续墙距离D的改变而引起的工况4下第一道内支撑轴力变化对比图，图6为工况5下第一道内支撑轴力变化对比图，图7 为工况5下第二道内支撑轴力变化对比图.通过观察不难发现，内支撑轴力对超载距离地下连续墙距离D较敏感，且随着D的不断增大而有下降的趋势.具体来看，图5中，当D=5 m时，第一道内支撑轴力数值为813 kN，当D=6 m时，第一道内支撑轴力数值为613 kN，两者轴力值相差为200 kN.说明坑外荷载距离变化对支撑轴力的影响较大.另外，当D取值分别为：7 m、8 m、9 m以及10 m时，轴力分别为：552 kN、525 kN、493 kN以及476 kN.图6中，当D=5 m时，第一道内支撑轴力数值为662 kN，当D=6 m时，第一道内支撑轴力数值为539 kN，两者轴力值相差为123 kN.这也说明坑外荷载距离变化对支撑轴力的影响较大.另外，当D取值分别为：7 m、8 m、9 m以及10 m时，第一道内支撑轴力分别为：471 kN、453 kN、410 kN以及395 kN.图7中，当D=5 m时，第二道内支撑轴力数值为552 kN，当D=6 m时，第二道内支撑轴力数值为481 kN，两者轴力值相差为71 kN，也说明坑外荷载距离变化对支撑轴力的影响较大.另外，当D取值分别为：7 m、8 m、9 m以及10 m时，第二道内支撑轴力分别为：463 kN、441 kN、405 kN以及383 kN.由图5和图6还可以看出，第一道内支撑的轴力在工况4与工况5时相比，工况5时第1道支撑轴力有所减小，这可能是因为第2道支撑参与了受力的原因.因此，在基坑开挖支护过程中，要严格控制基坑边缘非必要堆载，确有需要也应尽量使得堆载远离基坑边缘，以此来减小非对称荷载对基坑开挖的影响，同时也可以利用不同工况下内支撑轴力的变化规律对基坑支护体系设计参数进行优化.

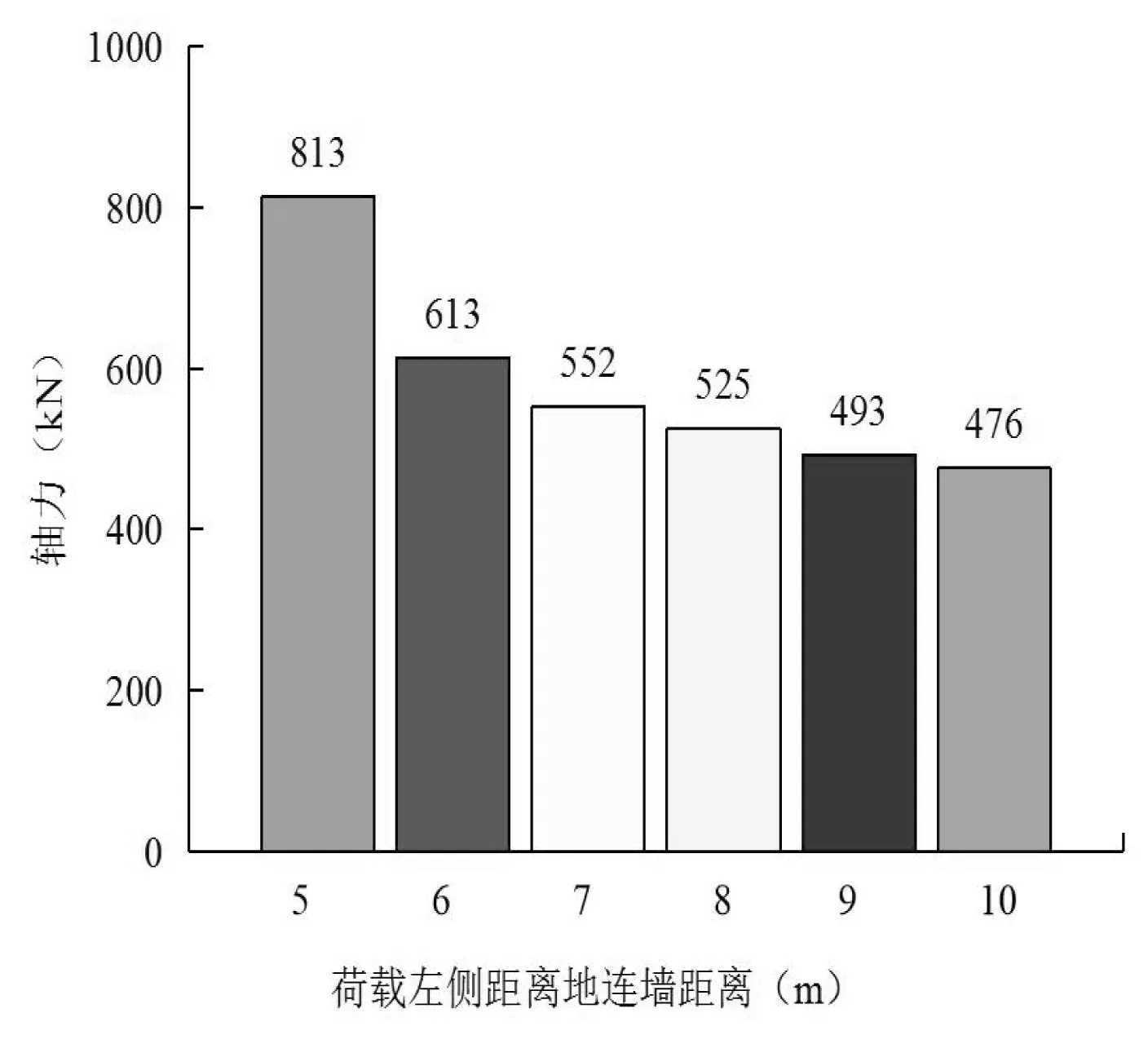
图5 工况4下第一道内支撑轴力变化图

图6 工况5下第一道内支撑轴力变化图

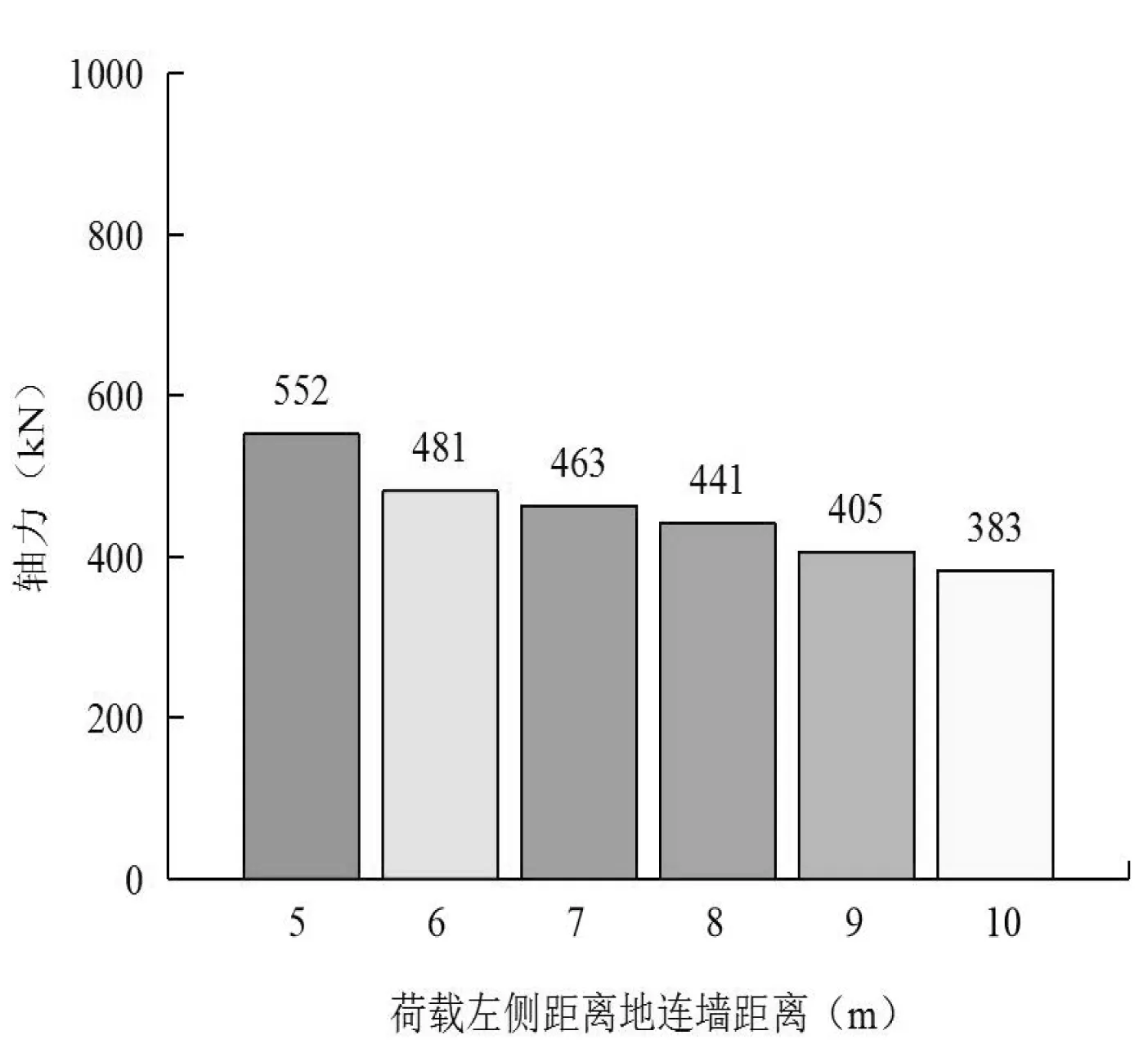
图7 工况5下第二道内支撑轴力变化图

4.2 坑外地表竖向变形分析

图8为超载距离地下连续墙距离D的改变而引起的工况5下基坑右侧地表竖向变形对比图，由图8 可见，总体上，基坑右侧地表竖向变形表现为“凹槽型”地表沉降，地表沉降值对超载距离地下连续墙距离D的大小较为敏感，有随着超载距离地下连续墙距离D的增大而减小的趋势，但最大沉降出现的位置在靠近右侧地下连续墙约4 m的位置.具体来看，当D=1 m时，基坑开挖引起的地表沉降最大，最大值约为11.9 mm，当D=9 m时，基坑开挖引起的地表沉降最小，最大值约为6.9 mm，约减小42%，可见超载距离地下连续墙距离D的改变对坑外地表竖向变形有较大影响.此外，当D分别为3 m、5 m以及7 m时，基坑开挖引起的最大地表沉降分别约为10.2 mm、9.1 mm以及8.3 mm.由图8还可以看出，超载距离地下连续墙距离D的增加也会导致距离地下连续墙顶部的地表土体沉降值也有不断减小的趋势，相较而言地下连续墙附近土体地表沉降值较小，这可能是因为地下连续墙与其接触的土体之间会产生摩擦力的作用，这种摩擦力会阻碍附近土体的竖向变形，这种阻碍效果也随着距离地下连续墙距离的增大而逐渐减弱.因此在类似基坑工程设计和施工时应重视非对称荷载对基坑附近地表沉降带来的不良影响.

图8 工况5下基坑右侧地表竖向变形对比图

5 结论

本文依托合肥某管廊基坑工程，采用MIDAS/GTS对基坑开挖及支护全过程进行数值模拟，研究了非对称荷载作用下基坑开挖引起的地下连续墙水平变形规律，模型计算结果与实测数据吻合良好，在此基础上研究了荷载距离D的改变对内支撑轴力及坑外地表沉降的影响，得出以下结论：

(1)通过修正摩尔库仑本构关系型模拟土体，可以较好地反应基坑开挖过程中的受力变形特性，模拟结果与实测结果吻合良好.

(2)偏压基坑两侧地下连续墙均产生向基坑内侧的水平变形，变形规律呈“凸鼓状”，最大变形位置在地下连续墙深度约为6 m的位置，且受压侧的地下连续墙变形明显大于非受压侧.因此，偏压基坑设计中宜增强受压侧围护结构的受拉侧配筋，以增强支护结构抵抗变形的能力，进而减小施工风险.

(3)超载不仅增大近超载侧地下连续墙的水平位移，还会引起远侧地下连续墙顶部出现远离基坑的位移；超载作用距离坑边距离的大小对支护结构安全尤为重要.当偏压距离D逐渐增大时，支撑轴力和地表沉降均有逐渐减小的趋势，因此在类似基坑设计施工时要充分重视超载位置对基坑开挖的影响，并在必要的时候采取有针性的措施减小非对称荷载对基坑开挖的不良影响.