基于复杂网络理论的城市公交网络鲁棒性分析与优化

赖 强，张宏昊，王徐盱

华东交通大学 电气与自动化工程学院，南昌 330013

公交出行的特点在于人流量大且频繁，相较于其他出行方式价格也很亲民，可以便捷地通往目的地。不同于需要考虑地理环境的航空系统和地铁系统，公交系统可以很轻易地通往整个城市的各个地方，通过建立城与城之间的公交路线也可以实现公交覆盖大范围化，这对于发展相对落后的城市是十分有意义的。因此如何合理地设计公交网络成为研究者们的热门议题[1]。

通过复杂网络相关知识可以对系统中个体与整体的关系有更清晰的认识，能够促进人们对电力系统和交通系统的改造[2-4]。Chen等人介绍了网络可控鲁棒性的定量测量方法，并对随机图网络、无标度网络、多重并发网络、随机三角形网络、随机直角网络、Q-Snapback网络六种网络模型进行了实验比较，结果表明多环结构可以提高网络可控鲁棒性[5]。Clemente和Cornaro提出了一种叫作有效阻力中心度的网络鲁棒性指标，定义为删除顶点（边）而导致的Kirchhoff指数的相对差，该指标能够体现特定顶点或特定边对网络鲁棒性的影响[6]。Safaei等人提出了一种基于香农熵概念的重构机制，用于简化复杂的网络配置以提高网络弹性[7]。Shang证明了网络的鲁棒性与网络拓扑结构、攻击方式、采样方法和数据丢失量等因素有关，强调了采样方法对网络鲁棒性的影响[8]。Man等人提出了一种新的基于残差度的边缘定位方法，通过对比证明该方法能够有效提高复杂网络结构能控性[9]。

经过站点的交通工具数量可以转化为复杂网络中的度分布；乘客从起始站点到最终站点所需要的最短途径可转化为复杂网络中的最短路径；站点每天的客流量可以转化为复杂网络中的权重等能说明公交网络本质上就是一个复杂网络[10]，一种基于复杂网络理论的公交网络研究方法便应运而生。Alvinsyah和Hadian提出了一种新的网络需求分析模型，通过分析得到了各快速公交通道在高峰时段的车流量、客流量[11]。Tian等人调研了中国97个大中城市的公共交通网络，构建了公交站网、公交网和公交线网三种类型的网络模型，并对其结构特点进行了分析，结果表明城市经济的发展与交通网络的发展有着很强的相关性[12]。Jin等人介绍了一种基于数据挖掘的位置最大似然估计方法和一种单元空间收集机制，探讨了北京市的公交分布情况，结果表明北京市公交站点的空间分布是由中心向周边城市地区递减的，公交资源的配置与公交乘客的需求存在差异[13]。Zhang提出了一种与平均度有关的移位幂律分布，用于拟合度分布。此外还引入加权平均最短路径和传输效率用于评价公交网络，结果表明所引入的指标能够有效地反映公交网络的特性[14]。

公交网络鲁棒性指的是站点遭破坏后公交系统维持正常运转的能力，研究公交网络鲁棒性的目的在于优化交通整体构造，减少交通拥堵。对公交网络的研究多集中于网络拓扑结构的性质，对于网络鲁棒性的优化研究较少。本文从8684（https：//www.8684.cn）网站上获得某市公交线路数据，通过Python软件建立了公交网络拓扑结构模型，采用连通度、最大连通子图的相对大小、网络效率作为鲁棒性评价指标，通过节点度攻击模式和随机攻击模式攻击网络，结果表明该市公交网络在随机攻击模式下鲁棒性较好，而在节点度攻击模式下鲁棒性较差。在采用介数加边、度数加边和随机加边策略对网络进行鲁棒性优化后，以网络效率作为优化效果判定指标，对比得出当加边率较小时，随机加边与低介数低度数加边策略都能提升网络鲁棒性且提升效果差别不大；随着加边率增大，低介数低度数加边策略对网络鲁棒性提升效果要优于随机加边策略；高介数高度数加边策略不能提升网络鲁棒性。

1 网络拓扑特性

描述网络拓扑结构特征的几何量可归纳为最短路径、介数、度分布、平均度、聚集系数等[15]。本文就节点度、聚集系数、点介数进行说明。

（1）节点度

节点度是描述拓扑结构最基本的术语，是指网络中节点所拥有的边数，在拓扑结构图中可直观表现为节点的大小，表述如下：

式中，N为自然数，i、j为网络中任意两个节点，e为i、j之间的边数。在公交网络中将经过节点的公交数作为节点的度数，通过的公交数越多，节点在拓扑图中越大。

（2）聚集系数

节点i的聚集系数是指i与网络中剩余n个节点间的连接概率，定义为实际连接数目m与理论连接数n(n-1)/2的比值。对于整个网络来说节点聚集系数的算术平均值即为网络的聚集系数，表述如下：

（3）点介数

点介数是体现网络中节点影响力大小的参数，对于寻找关键节点和规划路线有着重要作用，表述如下：

式中，dij为节点i与j之间的最短路径数目，dinj为在节点i与j的最短路径中经过节点n的路径数目。

2 网络鲁棒性定义与指标

2.1 鲁棒性定义

在移除部分节点后若网络剩余节点仍保持大部分相连，则称该网络具有鲁棒性[16]，具体是指网络遭到破坏仍能维持网络原有功能的特性。映射到公交网络上则表现为，站点或者路段遭到破坏无法正常工作时，整个公交网络能继续保持运作的能力。

2.2 攻击模式

公交网络节点多、线路多的特点决定了公交网络能承受攻击并保持正常运作，但对特意的、有目的性的攻击承受能力较弱。基于这个特性设置了两种攻击模式，具体如下：

（1）节点度攻击模式：按照节点度的大小排序，依次删除度数较大的点，在节点被删除后该节点与其他节点的连线相应被删除。

（2）随机攻击模式：随机删除网络中的节点，在节点被删除后该节点与其他节点的连线相应被删除。

2.3 鲁棒性指标

对鲁棒性的评价需要采用适合的指标，本文采用连通度、最大连通子图大小和网络效率作为鲁棒性的评价标准。

（1）连通度

连通度[17]指的是网络的实际边数与理论最大边数的比值，对象是整个网络而不是某个区域，受攻击后连通度越大，节点之间的连通率越大，网络的应变能力越强，鲁棒性越大。表述如下：

式中，|D|为公交网络拓扑结构图的边数，|Vd|为拓扑结构图中节点的个数，即站台的总数。

（2）最大连通子图的相对大小

用最少的边将网络的所有节点连接的子图叫作最大连通子图[18]。系统受攻击后最大连通子图的大小也会相应改变，一定程度上可以反映网络内部结构的变化。表述如下：

式中，|V′d|为最大连通子图中节点的数目。

（3）网络效率

网络中节点对间效率的平均值被称作为网络效率[19]。网络效率越高，网络的连通可靠性也高，网络的鲁棒性越高。表述如下：

式中， ||V d为节点总数，d i j为节点i到节点j的最短路径。

（4）节点失效比

节点失效比K定义为网络中失效节点数量 ||V与网络总节点数量 ||V d的比值。表述如下：

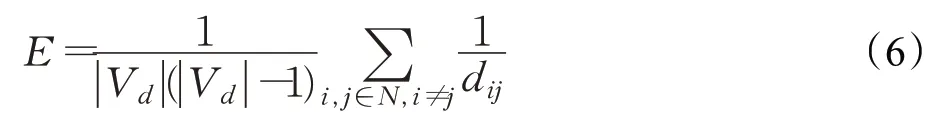
该指标反映了网络受攻击程度的大小。

3 网络鲁棒性分析

公交系统可分为线路与站点两个元素，研究侧重点不同建模方法也不同。本文所建立的公交网络拓扑结构模型将遵从以下原则：（1）公交站点作为网络中的节点，其度数以公交经过站点的数量为基准，在结构图中显示为节点的大小；（2）由于散点和过于偏远的节点对于整体网络的影响微乎其微，在分析过程中此类节点会被删除；（3）网络中分布较散且较小的环状线路将看作一个整体节点。某市公交网络拓扑结构模型如图1所示。

图1 某市公交网络拓扑结构图Fig.1 Topological structure of urban public transport network

该市公交数据是从8684（https：//www.8684.cn）网站上获得，截止获取时间为2020年6月5日。共有294条公交线路与2 369个公交站点，在拓扑结构图中节点大小代表着节点度大小，指的是通过节点的公交数目。处于中心地带的公交站度数较大，都在15以上。除了中心地带外大部分节点的度分布在1~7之间，度数在10以上的点占整体节点比例较少，平均度为2.614 6，说明整体网络存在可优化处。

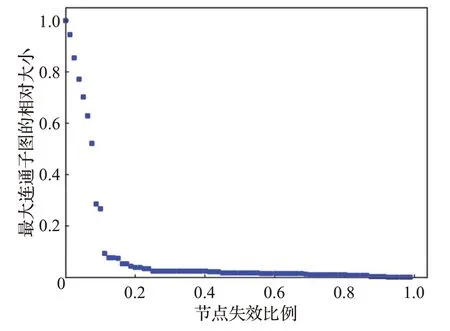
图3 最大连通子图的相对大小（度攻击）Fig.3 Telative size of the largest connected subgraph（degree attack）

图2~图4为在节点度攻击模式下，公交网络的连通度、最大连通子图的相对大小和网络效率的变化图。从图中可以看出，在网络失效节点达到10%时，连通度降为原网络的25%，而最大连通子图的大小与网络效率已经接近于0，此时公交网络基本处于瘫痪状态。

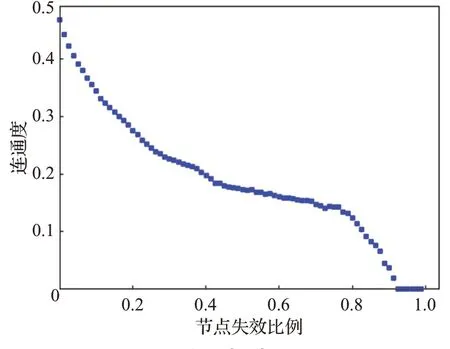
图2 连通度（度攻击）Fig.2 Connectivity（degree attack）

图4 网络效率（度攻击）Fig.4 Network efficiency（degree attack）

图5~图7为在随机攻击模式下，公交网络的连通度、最大连通子图的相对大小和网络效率的变化图。从图中可以看出，当网络失效节点达到40%时，连通度降为原网络的30%，而最大连通子图的大小与网络效率已经接近于0，公交网络基本处于瘫痪状态。

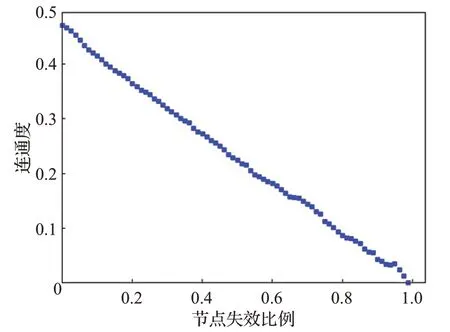
图5 连通度（随机攻击）Fig.5 Connectivity（random attack）

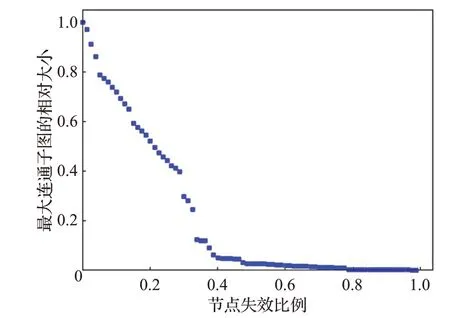
图6 最大连通子图的相对大小（随机攻击）Fig.6 Relative size of the largest connected subgraph（random attack）

图2~图7进行对比可以得出，在随机攻击策略下，该市公交网络鲁棒性较好，可以抵御较大程度的攻击；在蓄意攻击下该市公交网络的鲁棒性较差，被攻击后网络将有瘫痪的风险。因此可以对网络进行优化，提升网络鲁棒性。

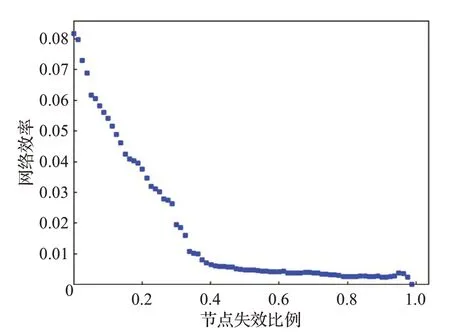
图7 网络效率（随机攻击）Fig.7 Network efficiency（random attack）

4 网络鲁棒性优化

4.1 加边策略

该市公交网络的节点分布较散，整体平均度小，因此增加节点的平均度对于网络整体鲁棒性的提升有很大帮助，可采取对网络加边的方式来提升网络节点平均度[20]。按照不同的方式加边策略可分为以下几种：

（1）按高介数加边（HBA）：对节点的介数进行计算，按照从高到低的顺序依次选取两个节点增加一条边，不允许出现相同边以及单独成环的情况，达到加边数时停止加边。

（2）按低介数加边（LBA）：对节点的介数进行计算，按照从低到高的顺序依次选取两个节点增加一条边，不允许出现相同边以及单独成环的情况，达到加边数时停止加边。

（3）按高度数加边（HDA）：对节点的度数进行计算，按照从高到低的顺序选取两个节点增加一条边，不允许出现相同边以及单独成环的情况，达到加边数时停止加边。

（4）按低度数加边（LDA）：对节点的度数进行计算，按照从低到高的顺序选取两个节点增加一条边，不允许出现相同边以及单独成环的情况，达到加边数时停止加边。

（5）随机加边（RA）：随机选取两个节点增加一条边，不允许出现相同边以及单独成环的情况，达到加边数时停止加边。

定义加边率为：

式中，L x为加边数量，L为原网络边数。

由于节点遭受攻击后节点的边也会被删除，若选取的两个节点间已经存在边，在这个基础上再加边对网络鲁棒性提升是没有意义的。因此添加新规则，在选择节点的时候若A点与B点间已有边相连，则会跳过B点使A点与下一个点配对，即优先选择不存在连边的点进行加边，可以提高加边效率。

4.2 优化模型分析

不同的加边策略对应的攻击模式不同，具体如下：

（1）以介数作为参数的加边策略采用度攻击模式，依次删除度数较大的点，在节点被删除后该节点与其他节点的连线相应被删除。

（2）以度数作为参数的加边策略采用介数攻击模式，依次删除介数较大的点，在节点被删除后该节点与其他节点的连线相应被删除。

（3）随机加边策略采用随机攻击模式，在节点被删除后该节点与其他节点的连线相应被删除。

图8是加边率10%时五种加边策略对应的网络效率图。由图8可以得出，与原网络相比，高介数加边（HBA）以及高度数加边（HDA）策略只是提高了网络的初始网络效率，从8%提高到了12%，对网络的整体鲁棒性并没有提升；低介数加边（LBA）、低度数加边（LDA）和随机加边（RA）策略对网络的初始网络效率和整体鲁棒性都有很大的提升，使网络瘫痪的失效节点比从10%提升到了20%，网络整体鲁棒性提高了一倍，且三种策略之间提升效果相差不大。

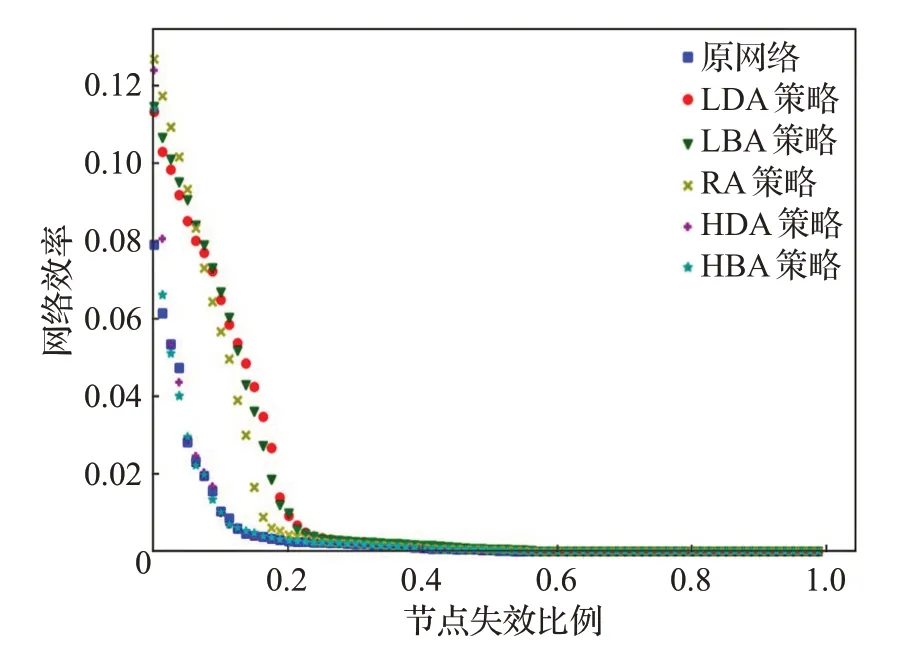
图8 加边率10%网络效率图Fig.8 Network efficiency with 10%edge addition rate

图9是加边率20%时五种加边策略对应的网络效率图。由图9可以得出，高介数加边（HBA）和高度数加边（HDA）策略对整体网络鲁棒性没有提升；低介数加边（LBA）和低度数加边（LDA）策略提升了整体鲁棒性，使网络瘫痪的失效节点比从10%提升到了30%，网络整体鲁棒性提高了两倍；随机加边（RA）策略也提升了整体鲁棒性，使网络瘫痪的失效节点比从10%提升到了20%，网络整体鲁棒性提高了一倍。

从图8和图9对比可以得出，对网络采取加边策略可以提升网络鲁棒性。低加边率下采用随机加边（RA）、低介数加边（LBA）和低度数加边（LDA）策略对网络鲁棒性都有提升且提升效果差别不大；高加边率下低介数加边（LBA）和低度数加边（LDA）策略比随机加边（RA）策略对网络鲁棒性提升更大；高介数加边（HBA）和高度数加边（HDA）策略对网络鲁棒性没有提升。

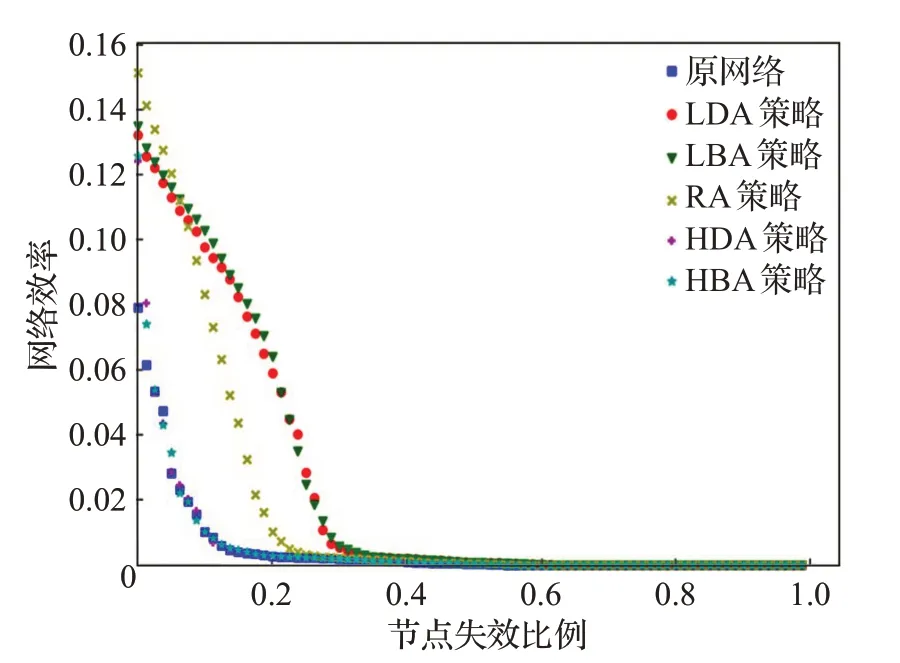
图9 加边率20%网络效率图Fig.9 Network efficiency with 20%edge addition rate

5 结论

本文在8684（https：//www.8684.cn）网站上获取了某市公交路线数据，基于Python软件仿真获得了该市公交网络的拓扑结构模型，采取节点度攻击模式与随机攻击模式进行攻击，选取连通度、最大连通子图的相对大小以及网络效率作为鲁棒性指标。结果表明，在随机攻击模式下该市公交网络鲁棒性较好，在节点度攻击模式下网络鲁棒性较差。之后采取了高度数、高介数、低度数、低介数和随机加边这五种策略对网络进行加边处理。通过对比得出，高度数以及高介数加边策略对于网络整体鲁棒性没有提升；低度数以及低介数加边策略对于网络整体鲁棒性提升较大，且加边率越大提升效果越为明显；随机加边策略也能提升网络整体鲁棒性，但提高加边率对鲁棒性提升效果影响较小。

从以上结果可以得出，当车流量较大的公交站台停止运作时若不及时修复处理，整个公交网络将面临瘫痪的危险，会对人们的出行带来很大的困扰。因此对于交通部门来说，车流量较大的公交站台应加以重视，重点维护，以保证整个公交网络的流通性，避免出现突发状况。公交网络模型的鲁棒优化给交通部门改善交通提供了思路，从理论上来说，在整改率不大的情况下，选取相对改造较为方便的站点进行整改可以提升整体交通的鲁棒性，且资源消耗较低；整改率较大的情况要选择低度数低介数的站点进行整改，具体实施应根据当地实际情形进行安排。