应用BWP指标的差分隐私保护k-means算法

张亚玲，屈玲玉

西安理工大学 计算机科学与工程学院，西安 710048

随着大数据和信息技术的快速发展，数据挖掘成为当前大数据环境下获取信息的重要方法[1]。聚类分析是一种经典的数据挖掘方法，允许从大量的数据中挖掘隐含的、有价值的知识和规则。许多企业收集了各领域的大量数据，利用聚类分析等技术对这些数据进行处理，以便开展科学研究、推送广告等，通过聚类可以提高其服务质量。然而，聚类分析通常包含用户数据，如果这些数据被不法分子加以利用，将会对个人隐私产生严重的威胁。因此，如何在聚类分析过程中保护用户的个人隐私已逐渐成为数据挖掘和信息安全领域中的热点问题。

针对以上问题，早期研究提出了基于等价类的kanonymity[2]及其一系列扩展模型。但这些模型没有一个严格的数学公式可以证明其隐私保护水平，并且需要不断改进来抵御新的攻击，如背景知识攻击[3]和合成攻击[4]。基于此背景，2006年，Dwork提出了差分隐私（differential privacy，DP）[5]的概念。在此定义下，对数据集的处理结果对于具体某个记录的变化是不敏感的，单个记录在数据集中或者不在数据集中，对计算结果的影响微乎其微，因此攻击者无法通过观察计算结果而获取准确的个体信息[6]。同时，差分隐私建立在严格的数学定义之上，并对隐私披露风险给出了定量化的表示和证明。随后，Dwork等人持续完善和补充了差分隐私理论[7-11]。何贤芒等人[12]提出了一个差分隐私保护攻击模型，并基于这个模型，提出了一个差分隐私保护技术的攻击算法和参数ε的选取计算公式。

作为最常用的聚类算法之一，k-means由于简单、高效等特点被广泛应用于各个领域，然而在算法执行过程中，对中心的更新过程会泄露数据集的信息，许多研究者进行了差分隐私k-means算法的研究。

Blum等人[13]提出了一种差分隐私k-means算法（DPK-means），在获取聚类结果的同时保护数据隐私，并在SuLQ平台上实现，但该算法全局敏感度较大，且没有给出迭代过程中如何分配隐私预算。Dwork[11]在Blum的基础上，从隐私预算分配的角度对其进行了完善，提出了两种隐私预算分配的方法。Nissim等人[14]提出了PK-means算法，给出了计算查询函数敏感度的方法，使k-means聚类中心满足差分隐私保护，但它的约束条件较多，实用性不强。李杨等人[15]针对隐私预算ε降低到一定值时聚类可用性变差的问题，提出了IDPKmeans算法，优化了初始聚类中心的选择，却忽视了离群点对最终聚类结果的负面影响。Yu等人[16]考虑了离群点的消极影响，在IDPK-means的基础上提出了OEDPKmeans算法，利用异常值检测算法，根据数据点的密度分布选择合适的初始中心，但是该算法时间复杂度较大，在某些数据分布下收敛速度较慢。Ren等人[17]为了提高DPK-means算法的聚类效率，提出了DPLK-means算法，该算法通过对原始数据集划分的每个子集执行差分隐私k-means算法来改进初始中心点的选择，但是聚类结果受数据分布影响较大，当数据集较小时，算法不能很好地工作。胡闯等人[18]在DPK-means算法的基础上，引入k-means++算法改进初始中心点的选择，但是该算法对于不规则的数据集会产生较差的聚类效果。樊一康等人[19]提出的TripleP K-means算法通过计算数据集中各点的最近邻超球半径以消除离群点的消极影响，但当隐私预算较小时，聚类效果不理想。Fan等人[20]针对传统的隐私预算分配存在迭代次数越多随机噪声越大的问题，提出了一种基于等差数列隐私预算分配的APDPK-means算法，在迭代过程中由大到小分配隐私预算，以保证其在迭代早期可以快速收敛。

从改进差分隐私保护k-means算法的隐私预算分配机制以提高聚类结果的可用性出发，本文引入BWP（between-within proportion）指标，提出一个改进的差分隐私k-means算法BDPK-means（BWP differential privacyk-means）。BDPK-means算法根据每一次迭代中不同聚类簇具有不同密度分布的特点，分配不同的隐私预算，避免聚类簇太小或者密度太大而添加过大的随机噪声，规避由于数据扰动造成聚类中心点偏移过大的问题，使隐私性和可用性达到一个较好的平衡。实验表明，本文BDPK-means算法在可用性与稳定性上优于现有的同类差分隐私k-means算法。

1 预备知识

1.1 差分隐私

差分隐私是一种基于数据失真的隐私保护技术，通过添加随机噪声干扰数据来保证数据具有一定的隐私性，同时保证原有数据的统计特性及可用性，以便进行数据分析等操作。

定义1（ε-差分隐私[5]）设有随机算法M,P M为M所有可能输出构成的集合。对于任意两个邻近数据集D和D′以及P M的任何子集S，若算法M满足：

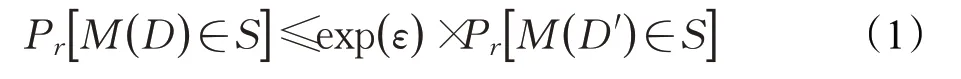
则称算法M满足ε-差分隐私保护。其中，D和D′是相差最多为一条记录的两个邻近数据集，参数ε称为隐私保护预算。隐私预算代表隐私保障的水平，越小的隐私预算提供越严格的隐私保护水平。

定义2（全局敏感度[7]）设有查询函数f:D→Rd，输入为一数据集，输出为d维实数向量。对于任意邻近数据集D和D′：

称为函数f的全局敏感度。‖‖1表示1-阶范数距离。

差分隐私有两种实现机制，Laplace机制与指数机制，其中Laplace机制适用于处理数值型数据，指数机制适用于非数值型结果。本文采用Laplace机制实现差分隐私保护。

定义3（Laplace机制[8]）给定数据集D，设有函数f:D→Rd，其中函数敏感度为Δf，那么随机算法M(D)=f(D)+Y提供ε-差分隐私保护，Y~Lap(Δf/ε)服从尺度参数Δf/ε的Laplace分布。

Laplace机制是通过向结果中加入服从Laplace分布的随机噪声来实现差分隐私保护。将位置参数为0、尺度参数为b的Laplace分布记为Lap(b)，其概率密度函数为：

此外，一个复杂的隐私保护问题通常需要多次应用差分隐私保护算法才能得以解决。在这种情况下，隐私预算两个组合性质对于聚类算法的隐私分配过程具有重要的意义。

性质1（序列组合性[21]）设有算法M1,M2,…,M n，算法的隐私预算分别为ε1,ε2,…,εn，那么对于同一数据集D，算法{M1,M2,…,M n}在D上构成的组合算法M(M1(D),M2(D),…,M n(D))提供ε-差分隐私，其中ε=

性质2（并行组合性[21]）设有算法M1,M2,…,M n，算法的隐私预算分别为ε1,ε2,…,εn，将D分为不相交的数据集D1,D2,…,D n，算法{M1,M2,…,M n}构成的组合算法M(M1(D1),M2(D2),…,Mn(D n))提供ε-差分隐私，其中ε=max(εi)。

1.2 差分隐私保护k-means聚类

基于差分隐私保护的k-means聚类算法旨在改变数据集中的任意一条记录时，各聚类簇中心和数据数目产生的相应变化不会泄露隐私信息。文献[19]提出的TripleP K-means算法考虑了k-means算法对离群点较敏感的缺点，对离群点进行修剪，实现了在单机环境和分布式环境下对k-means算法添加差分隐私的过程。文献[19]中有关离群点的定义如下：

定义4（r-最近邻超球半径[19]）对于RT上的数据集D={x1,x2,…,x N}，称任一数据点xi与离其最近的r个数据点在T维空间中构成的超球为x i的r-最近邻超球，这一概念原型为文献[16]中的r-最近邻区域。点x i与其超球中所有点的平均欧式距离为超球的半径。

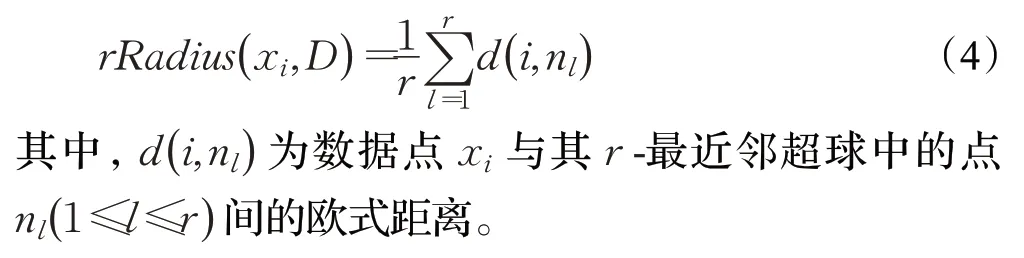
定义5（离群点及判定阈值[19]）离群点[16]是指数据集中与其他点显著不同的数据点。对于离群点的判定，设数据集中的稀有类由至多5%的数据点组成[22]，估计数据集D中离群点数目不超过N×0.05，其中N为数据集规模大小。记离群点的r-最近邻超球半径的判定阈值为T，取其值为数据集中r-最近邻超球半径最大的N×0.05个点的半径均值，从而认为r-最近邻超球半径超过阈值T的数据点为离群点。

文献[19]算法单机环境下的主要思想：

步骤1对数据集中的所有数据进行归一化处理，并且计算各点的r-最近邻超球半径，由此得出离群点判定阈值T。

步骤2从数据集中随机选取一个非离群点μ1′，然后从剩余的数据点中选取距离μ1′最近的floor(N/K)个非离群点（floor()为向下取整函数），与μ1′组成初始簇C1。算法重复这一过程，直至选出K个簇。

步骤3计算各簇中数据点总和与簇中数据点的数目，分别添加Laplace噪声，求各簇的均值作为初始聚类中心。

步骤4计算数据集中非离群点与各聚类中心的距离，并将这些数据点分配到距离最近的聚类中心所在簇中。记第k个中心的簇为C k，簇中数据点数目及总和分别为numk和sumk，分别向numk和sumk添加相同大小的随机噪声，并计算新的聚类中心点。

步骤5计算本轮和上一轮中K个聚类中心点的距离是否满足收敛条件，若满足，则算法终止，输出聚类结果，否则重复步骤2~步骤5。

隐私预算分配采用二分分配[11]的方法，即第一轮迭代分配ε/2的隐私预算，之后每次迭代消耗隐私预算的1/2。

实验过程中发现随着迭代次数的增加，隐私预算就会越小。由Laplace差分隐私保护机制的性质可知，产生的随机噪声就越大，从而导致聚类中心的偏移过大，影响最终的聚类结果。

2 BDPK-means算法

为了解决隐私预算ε较小时数据可用性较差的问题，本文提出了一种基于BWP指标的差分隐私保护kmeans聚类算法。算法的主要思想是使用BWP指标评估每次迭代中聚类的效果，考虑每轮迭代中不同簇有不同密度分布、不同大小等特点，为每轮迭代中不同的聚类簇分配不同的隐私预算，从而添加不同的随机噪声，以此来解决中心点严重偏离而造成聚类可用性差的问题。

2.1 BWP指标

BWP指标[23]是评价聚类结果好坏的一种方式。结合内聚度和分离度两种因素，评价不同算法或者算法不同运行方式对聚类结果所产生的影响。其计算公式如下：

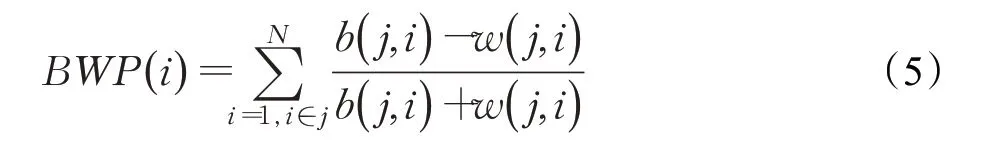
其中，N为数据集规模大小，j表示类标，b(j,i)表示类间距离，w(j,i)表示类内距离。类间距离b(j,i)为样本i到其他每个类中样本平均值中的最小值，类内距离w(j,i)为该样本到第j类中其他数据对象距离的平均值，公式如下：

其中，n k代表第k个簇的样本点数量。BWP k值越大聚类效果越好，反之越差。

2.2 BDPK-means算法设计

假设数据集D={x1,x2,…,x N}，其包含N个具有d维属性值的数据点，算法可以将其划分为K个簇，聚类中心点记为u k(1≤k≤K)，隐私预算为ε，第k个簇在第t次迭代的随机噪声为

BDPK-means算法的主要步骤如下。

算法1主要分为三个阶段。首先计算数据集中每个数据点的r-最近邻超球半径，由此导出数据集中离群点的判定阈值T（第1~6行），然后在此基础上选取初始聚类中心（第7~12行），最后完成差分隐私聚类分析（第13~33行）。其中第20~32行使用BWP指标评估聚类每一次迭代中不同簇的密度分布，在隐私预算二分分配的基础上为不同的簇分配不同的权重，有针对地调整隐私预算分配，从而对每次迭代中的聚类中心点分别添加不同的噪声，尽可能降低噪声对聚类中心偏移的影响，提高聚类结果的可用性。

2.3 隐私性分析

定理1BDPK-means算法满足ε-差分隐私保护。

（4）由定义1、式（11）和式（12）可得：

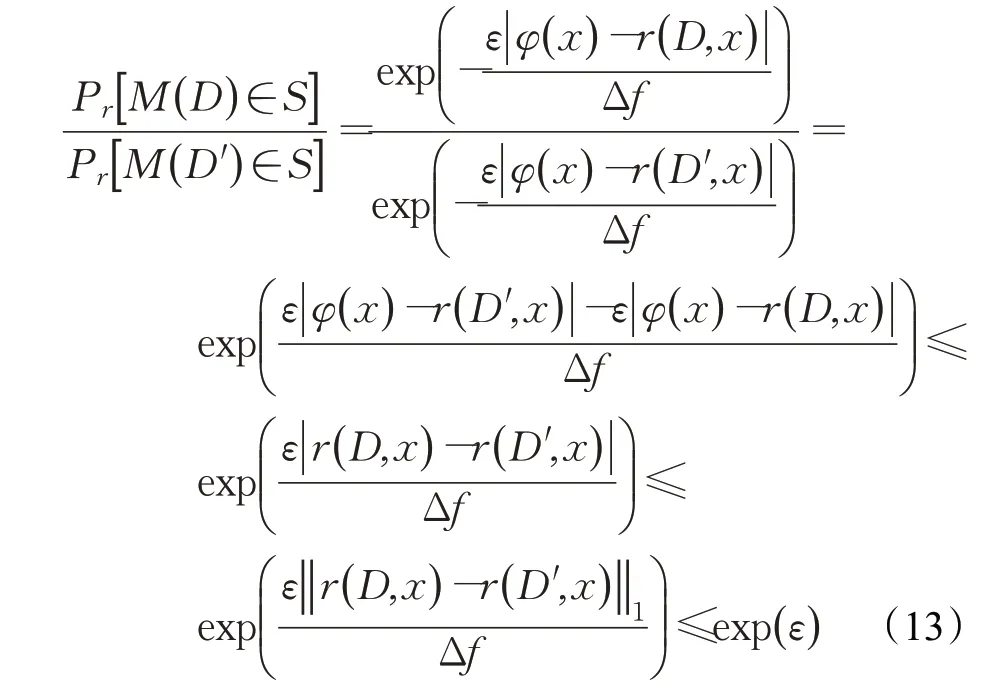
综上所述，由差分隐私定义可知，BDPK-means算法满足ε-差分隐私保护。

3 实验分析

3.1 实验环境及数据

本文使用Java语言进行模拟仿真实验，实验平台为Intel®CoreTMi3-3240 CPU@3.40 GHz处理器，6 GB内存，Windows10 64位操作系统。

本文选取了不同数量的数据集来进行仿真实验，实验所选择的数据集均来自UCI机器学习库，具体信息如表1所示。

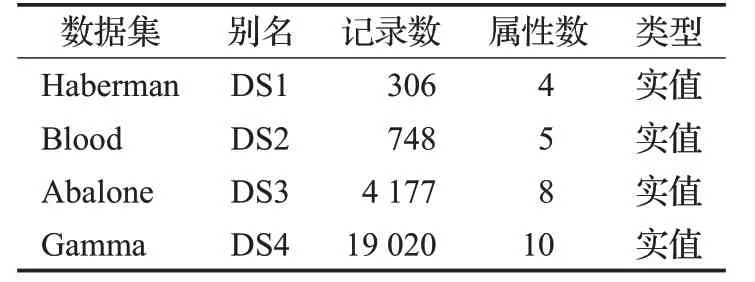
表1 数据信息Table 1 Data information

3.2 实验评价标准

（1）Purity

Purity（纯度）作为一种用来计算聚类划分结果正确率的常用指标，可以对聚类结果的优劣程度做出正确的判断。主要思想是计算被正确划分的样本数据的数量占整个数据集中所有样本数据数量的百分比。公式如下：

（2）F-measure

F-measure[24]是一种经典的衡量聚类结果有效性的评价指标。综合了信息检索与挖掘中的准确率（precision）和召回率（recall）。

F-measure取值为[0，1]，值越大表示两个数据集的聚类结果越接近，说明聚类结果可用性更好。

3.3 算法参数选取

由于计算离群点判定阈值和选取初始中心时，使用了r-最近邻区域的概念，参考文献[19]和文献[25]中的方法，以F-measure为目标函数对参数r进行调参并取最优。

3.4 实验结果分析

3.4.1 算法可用性分析

将本文提出的BDPK-means算法和文献[19]中的TripleP K-means算法（简称TDPK-means算法）、文献[20]中的APDPK-means算法在不同数据集下进行对比实验。

由于Laplace噪声的随机性，实验结果在同一隐私预算ε下，运行50次取平均值。图1~图4（a）和图1~图4（b）分别展示了在数据集DS1~DS4上运行三种聚类算法得到的Purity值和F-measure值的对比。

由图1~图4可知，随着隐私预算的增加，三种聚类算法的Purity值和F-measure值也在不断增加。这是因为随着隐私预算的增加，添加的噪声就会减小，聚类结果的可用性就会得到提高。本文算法与TDPK-means算法和APDPK-means算法相比，Purity值和F-measure值都有较大的提升，尤其在隐私预算较小时，聚类性能优势表现更为明显。

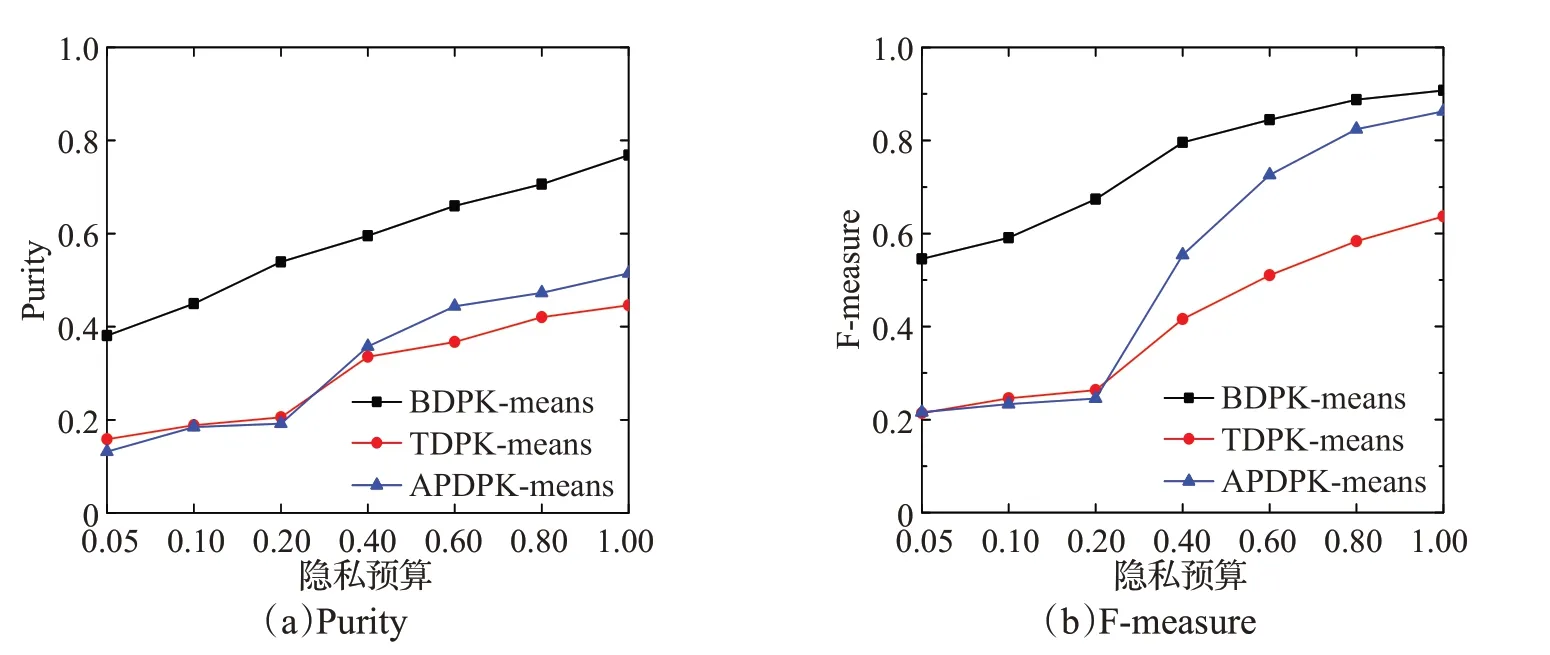
图1 DS1上运行的结果Fig.1 Results on DS1

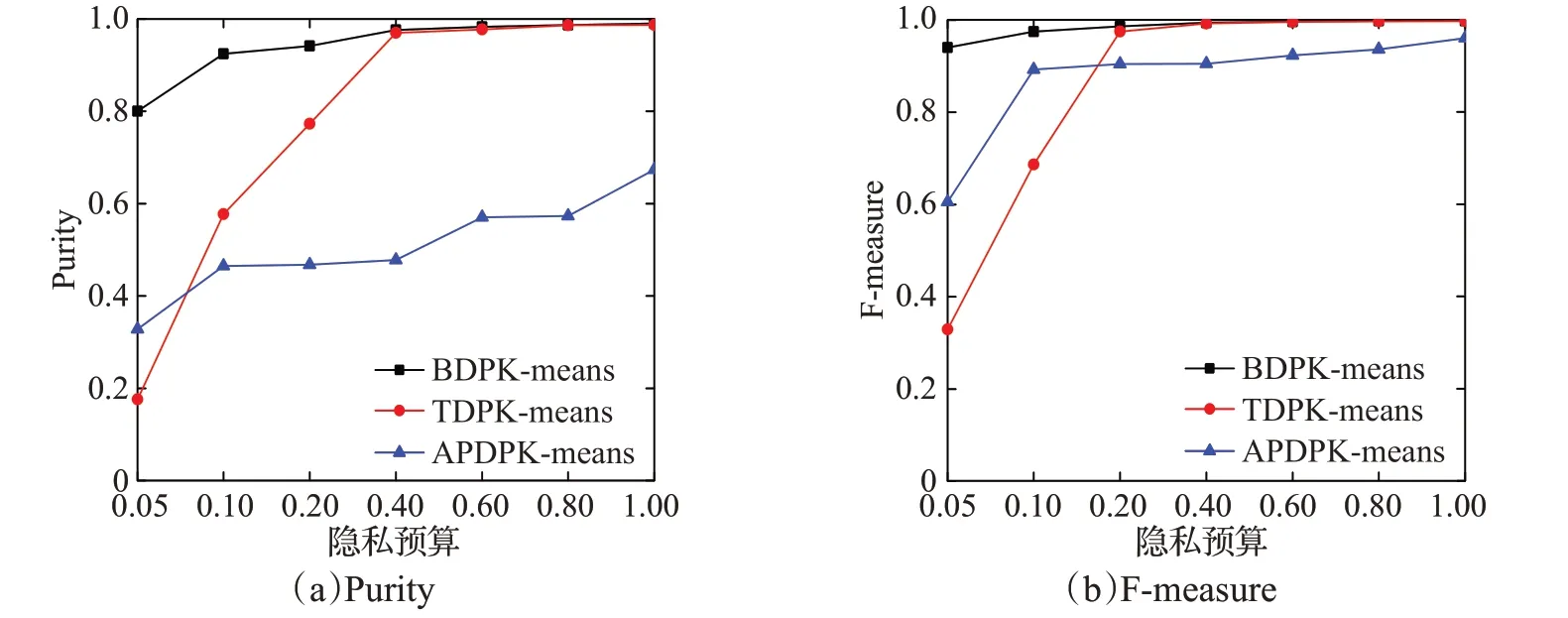
图4 DS4上运行的结果Fig.4 Results on DS4

具体来说，当隐私预算为0.05时，对于DS1，Purity值平均提高了0.24，F-measure值平均提高了0.33。DS2中，Purity值平均提高了0.21，F-measure值平均提高了0.40。针对DS3，F-measure值平均提高了0.20。可以注意到，DS3中，本文算法和其他两种聚类算法的Purity值，在隐私预算为0.05时，改进幅度不是很大。这是由于当隐私预算为0.05时，添加的Laplace噪声过大导致的。此时并不能很好地表现出该数据集的聚类特性，但是随着隐私预算的增加，本文算法还是优于其他两种算法。对于DS4，当隐私预算为0.05时，Purity值平均提高了0.54，F-measure值平均提高了0.47。

图2 DS2上运行的结果Fig.2 Results on DS2

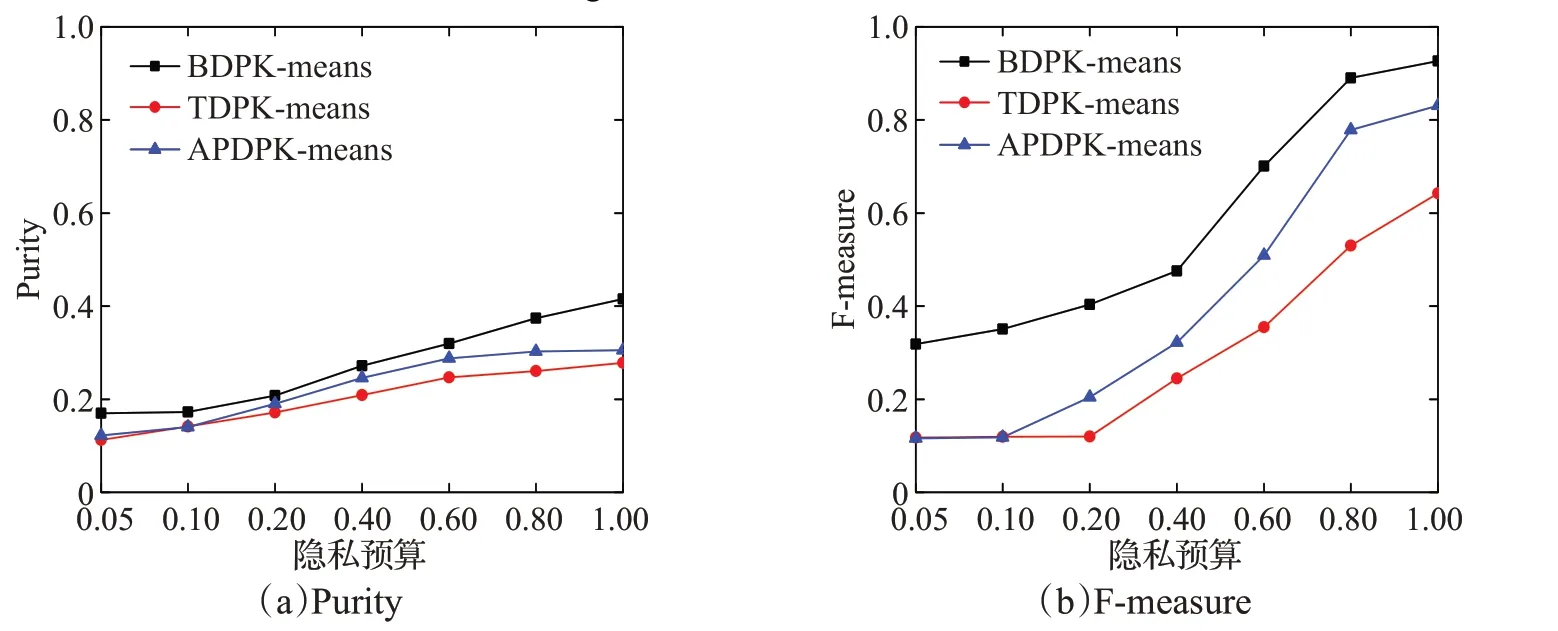
图3 DS3上运行的结果Fig3 Results on DS3

因此，在相同的隐私保护水平下，BDPK-means算法在不同数据集上的性能要优于其他两种聚类算法。

3.4.2 算法稳定性分析

本次实验通过计算算法的平均迭代次数来衡量算法的稳定性。对比算法依然采用文献[19]和文献[20]中的算法。三种算法的稳定性对比如图5所示。

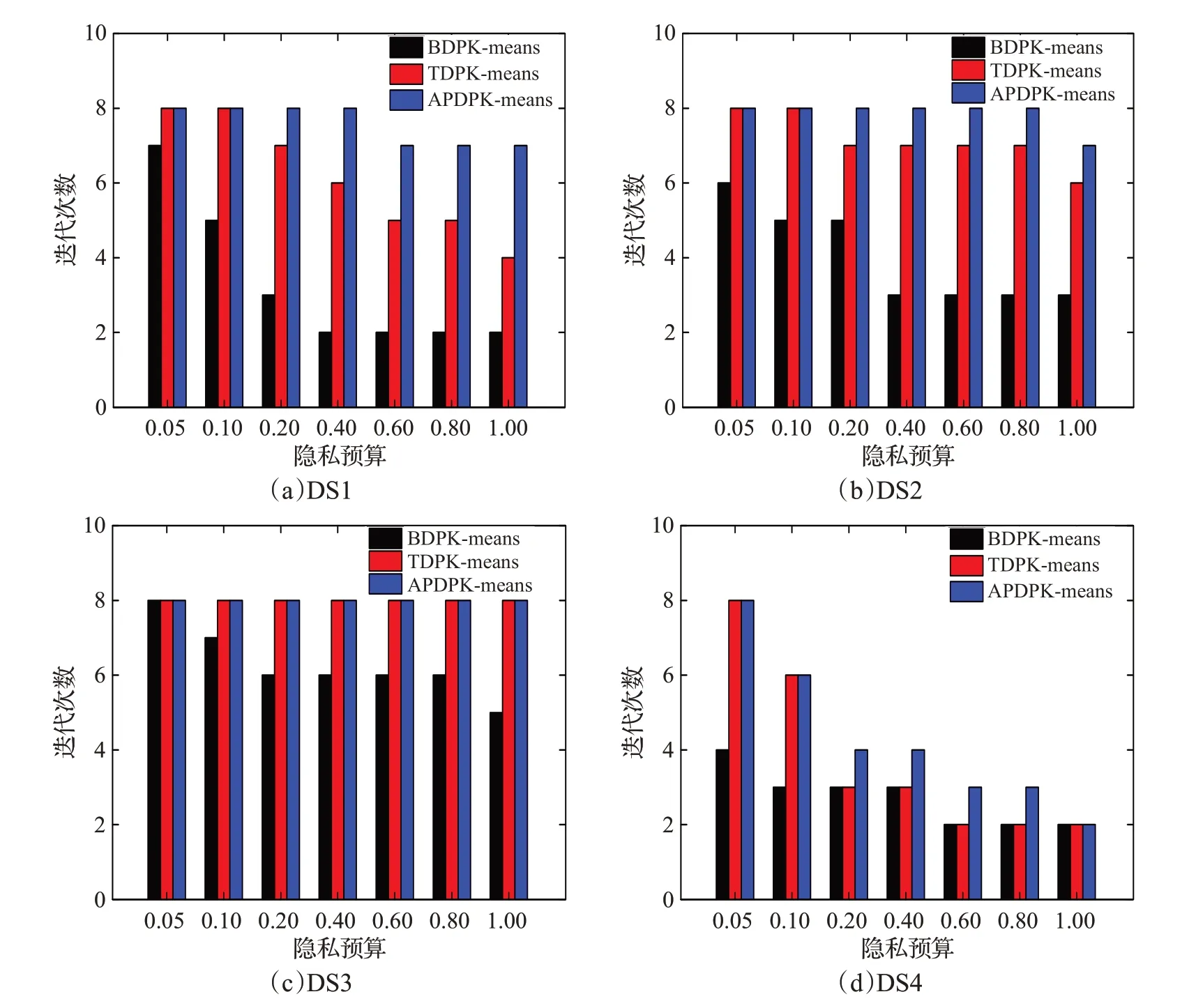
图5 迭代次数对比Fig.5 Comparison of iteration number

由图5实验结果可以看出，在四个数据集中，本文算法的迭代次数明显降低，表明本文算法收敛速度较快。随着隐私预算的增加，三种聚类算法的迭代次数都逐渐减少，当隐私预算达到设定的最大值时，本文算法基本达到收敛状态。此外，从图中还可得知，本文算法迭代次数波动不大，在稳定性上要优于其他两种聚类算法。

4 结束语

本文针对差分隐私k-means算法中存在隐私预算较小时聚类结果可用性差的问题，通过引入聚类评价指标BWP评估聚类效果，为具有不同密度分布的聚类簇分配不同的权重，在一次迭代中，动态地为不同的簇分配不同的隐私预算，从而添加不同大小的随机噪声，避免了因为差分隐私保护导致数据严重失真的问题，使得保护个体隐私的同时保持了较高的数据可用性。通过一系列对比实验，结果表明，本文算法不仅提高了数据的可用性和准确性，而且减小了迭代次数，提高了聚类结果的稳定性。但是本方案是在单机环境下完成的，当数据量较大时，会耗费大量的时间。因此，在未来的研究中，应重点考虑如何将本文算法扩展到分布式环境以解决大数据背景下所面临的隐私泄露问题。