融合互利共生和透镜成像学习的HHO算法

陈 功，曾国辉，黄 勃，刘 瑾

上海工程技术大学 电子电气工程学院，上海 201620

近年来，随着计算机技术的发展，群智能优化算法在图像[1]、电力[2]、医学[3]、服务[4]等领域中有了广泛应用。学者们通过模拟自然界中一些事物或生物的运动及行为规律，提出了许多高效的群体智能算法，如粒子群算法（particle swarm optimization，PSO）、灰狼优化算法（grey wolf optimization，GWO）、飞蛾火焰优化算法（moth flame optimization，MFO）、正余弦优化算法（sine cosine algorithm，SCA）、鲸鱼优化算法（whale optimization algorithm，WOA）、哈里斯鹰优化算法（Harris hawks optimization，HHO）等。其中HHO是2019年由Heidari等人[5]提出的一种新型群智能优化算法，与其他群智能算法相比，HHO具有较强的全局搜索能力，且需要调节的参数较少。然而，同其他算法一样，哈里斯鹰算法仍存在收敛速度慢、易陷入局部最优的缺点。

为了改善群智能算法收敛速度慢、易陷入局部最优的缺陷，许多学者提出了改进：Mirjalili等[6]受昆虫群体多样性的启发，提出一种自治粒子群算法，该算法使用具有不同斜率、曲率的函数来调整社会和认知参数，增强了算法跳出局部极值的能力。龙文等[7]针对灰狼优化算法探索能力弱的缺点，受粒子群算法的启发，提出一种控制参数随机动态调整策略，平衡了算法的探索和开发能力。Komalpreet等[8]为了提高飞蛾火焰优化算法的性能，引入柯西分布函数和自适应步长以保持探索和开发之间的平衡，提出一种强化飞蛾火焰算法。仿真结果表明，强化飞蛾火焰算法的收敛速度更快，适应性更强。Gupta等[9]为了改善正余弦算法易陷入局部最优的缺陷，为候选解引入一种探索性搜索引导，提出一种记忆引导的正余弦算法，提高了算法的全局搜索能力。黄清宝等[10]在基本鲸鱼优化算法中加入同步余弦惯性权值，并引入多项式变异对最优位置鲸鱼进行扰动，增强了鲸鱼算法的寻优精度和稳定性。郭雨鑫等[11]在哈里斯鹰优化算法中引入随机收缩系数和惯性加权因子，有效提高了算法的求解效率和寻优性能。Song等[12]为增强哈里斯鹰优化算法的性能，引入两种高斯变异策略和一种布谷鸟搜索机制，成功提高了算法的收敛速度和寻优精度。Vikram等[13]针对哈里斯鹰优化算法易陷入局部最优的问题，考虑到正余弦算法较强的局部开发特性，提出一种混合正余弦的哈里斯鹰优化算法，仿真测试验证了所提算法的有效性。

以上文献在一定程度上提高了群智能算法的收敛速度和跳出局部最优的能力，但仍存在收敛精度低、开掘能力弱等缺陷。本文提出一种融合互利共生和透镜成像策略的哈里斯鹰优化算法（IHHO），从以下三方面进行改进：（1）在初始化阶段，利用Tent混沌提高初始种群多样性；（2）在探索阶段融入共生生物搜索思想，并引入惯性权重，增强种群信息交流，加快收敛速度；（3）采用透镜成像学习策略对种群进行扰动，提高种群多样性，促使算法跳出局部空间限制，继续搜索。通过对16个基准测试函数的测试对比，证明了改进策略的有效性；同时，将IHHO应用于图像分割问题中，仿真实验验证了该算法在实际工程应用中的可行性。

1 基本哈里斯鹰优化算法

HHO算法是模拟哈里斯鹰觅食行为的一种元启发式算法，该算法主要包括探索和开发两个阶段。

（1）探索阶段

在该阶段，哈里斯鹰通过两种方式寻找食物：

式中，Xrand(t)为随机选择个体位置；Xrabbit(t)为最优个体位置；r1、r2、r3、r4、q均为0到1的随机数；ub和lb为搜索空间的上下界；Xm(t)为种群平均位置，公式为：

（2）探索与开发的转换

哈里斯鹰根据猎物的逃逸能量在探索和不同开发策略间进行转换，逃逸能量因子定义为：

式中，E0为-1到1之间的随机数，T为最大迭代次数。

（3）开发阶段

在寻找到猎物后，哈里斯鹰会根据猎物的行为以4种不同的开发策略进行狩猎。定义r为[0，1]的随机数，用于选择不同的开发策略。

当 |E|≥0.5且r≥0.5时，哈里斯鹰采用软围攻策略进行位置更新：

其中，J为[0，2]之间的随机数。

当 |E|＜0.5且r≥0.5时，哈里斯鹰采用硬围攻策略进行位置更新：

当 ||E≥0.5且r＜0.5时，哈里斯鹰会采用更加智能的渐进式快速俯冲的软包围进行位置更新：

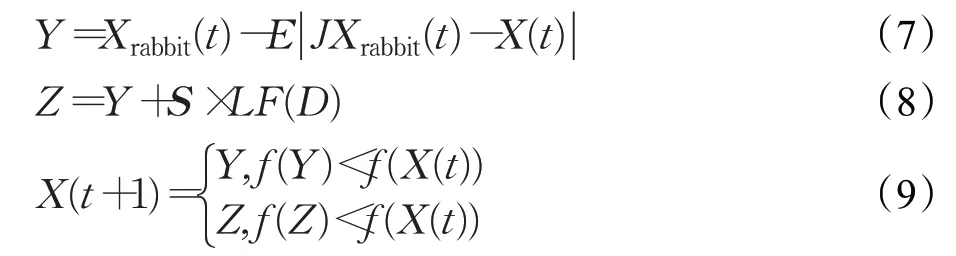
其中，S为D维随机向量，元素为[0，1]之间的随机数；f为适应度函数；LF为莱维飞行函数。

当|E|＜0.5且r＜0.5时，哈里斯鹰会采用渐进式快速俯冲的硬包围方式进行位置更新：

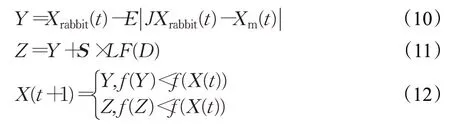
2 融合互利共生和透镜成像学习的哈里斯鹰优化算法

2.1 Tent混沌初始化种群

初始化种群是否均匀分布在搜索空间中，是影响算法收敛速度和寻优精度的一个重要因素。混沌变量具有随机性、规律性和良好的遍历，在保证种群多样性的同时，能够改善算法的全局搜索能力[14-15]。Logistic映射是一种常见的混沌模型，已经被广泛应用于优化问题中。然而，由图1所示混沌序列分布图可知Logistic映射在[0，0.1]和[0.9，1.0]的取值概率较大，因此算法受Logistic映射遍历不均匀的影响，寻优效率会降低；相较于Logistic映射，Tent映射能产生更加均匀的混沌序列。

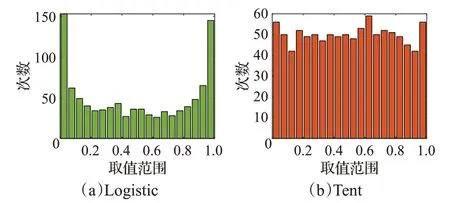
图1 混沌序列分布Fig.1 Frequency distribution of chaotic sequence

为了使初始哈里斯鹰种群均匀分布在搜索空间中，考虑到Tent映射具有良好的遍历性，利用Tent映射初始化种群。Tent映射公式如下：

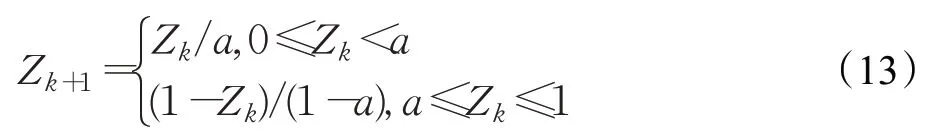
式中，a一般取0.4。将产生的混沌序列映射到解的搜索空间内：

式中，x id为第i只哈里斯鹰在第d维的位置；xU和xL分别为搜索空间的上下限；z id为式（13）产生的混沌序列。

在二维搜索空间中，假设种群规模为30，采用随机初始化和Tent混沌初始化的种群分布图如图2所示，相比随机序列，通过Tent混沌序列产生的初始种群能够更均匀分布在搜索空间中。

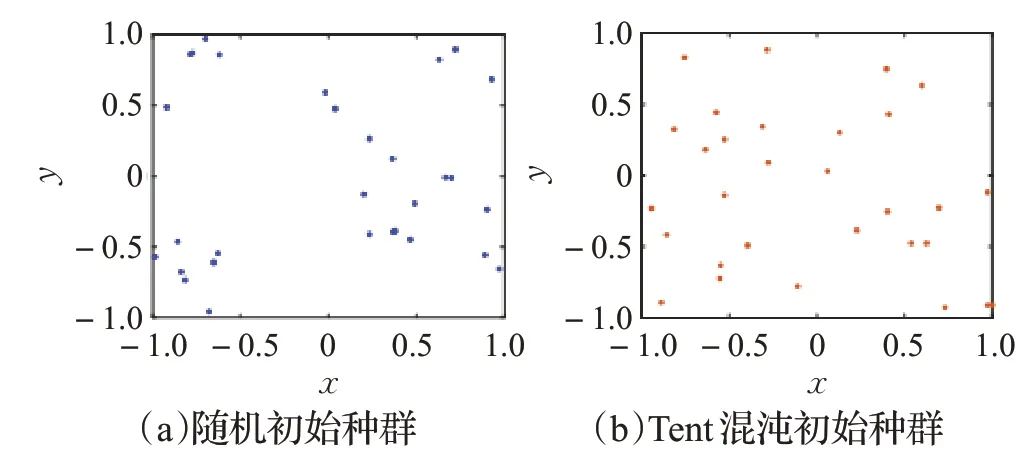
图2 初始化种群分布图Fig.2 Initialized population distribution graph

2.2 融合互利共生思想

HHO算法在探索阶段会移动到随机选择的哈里斯鹰位置附近，种群位置的更新受随机性影响较大，个体间缺乏信息交流，容易导致盲目搜索，造成算法收敛速度下降，寻优精度降低[16]。

共生生物搜索算法（symbiotic organisms search，SOS）是Cheng等[17]于2014提出的一种基于生物学中共生现象的启发式搜索算法。SOS算法主要分为互利阶段、共栖阶段和寄生阶段。在互利阶段，两只个体Xi和X j保持着交互关系，交互后的位置更新公式分别由式（15）和式（16）表示。

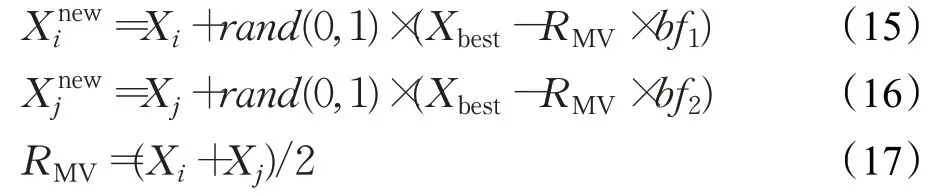
式中，Xbest为最优个体位置；bf1和bf2为利益因子，随机选择为1或2，表示可能得到部分受益或完全受益；RMV表示X i和X j的交互关系。

考虑到SOS在互利阶段，两只个体间具有较强的信息交流，本文将当前个体与随机选择个体进行交互，并加入最优哈里斯鹰进行引导搜索。在此基础上，引入惯性权重，提出一种改进的探索阶段搜索策略，公式如下：

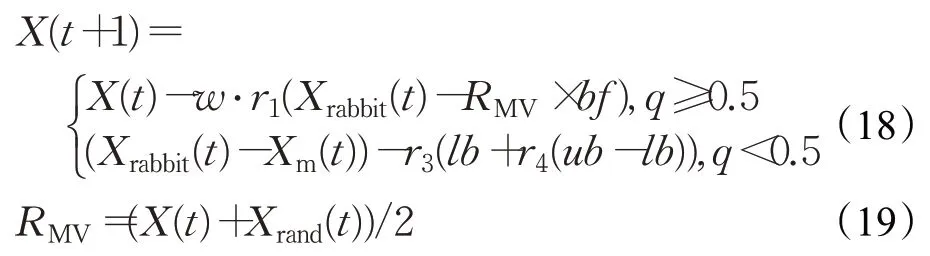
式中，Xrand(t)为随机选取的哈里斯鹰位置；r1为0到1的随机数；bf为利益因子；w为惯性权重，公式如下：

其中，wmax和wmin分别为惯性权重初值与终值。经大量仿真测试，当取wmax=1.2,wmin=0.4时测试效果最佳。

式（18）中，RMV为当前个体与随机选择个体的交互关系，改进后哈里斯鹰会以最优位置Xrabbit(t)和交互关系RMV为导向移动到当前位置附近。通过交互关系与最优哈里斯鹰的引导，当前个体与其他个体间的信息交流更加丰富，哈里斯鹰在探索阶段会根据收集到的信息向全局最优位置探索，避免了随机选择导致的盲目搜索。非线性递减的惯性因子使得算法在探索前期能够大范围搜索，在探索后期缩小搜索范围，同时加快收敛速度。

2.3 透镜成像反向学习策略

2.3.1 基于凸透镜成像原理的反向学习

反向学习是由Tizhoosh[18]提出的一种优化机制，其通过计算当前位置的反向解来扩大搜索范围，由此找到优化问题的更优解。将群智能算法与反向学习相结合能够有效提升算法的寻优性能，但是反向学习存在一定的缺点，例如在迭代后期反向学习无法使算法有效跳出局部最优，导致算法收敛精度不足。

为了克服一般反向学习的不足，受光的凸透镜成像原理启发，本文提出一种透镜成像反向学习策略，具体描述如下。

（1）光的凸透镜成像原理

当物体在焦点之外时，会在凸透镜另一侧成倒立的实像。其原理如图3所示。

图3 光的凸透镜成像原理图Fig.3 Convex lens imaging principle of light

由图3可得透镜成像公式：

式中，u为物距，v为像距，f为焦距。

（2）基于凸透镜成像的反向学习策略

如图4所示，以一维空间为例，x轴上解的搜索范围为[a,b],y轴表示凸透镜。假设有一个体P，在x轴上投影为x，高度为h，通过凸透镜成像可得到一个实像P*,P*在x轴上投影为x*，高度为h*。由此可得到个体x的反向个体x*。

图4 透镜成像反向学习策略示意图Fig.4 Opposition learning strategy based on lens imaging

图4中，个体x以O为基点得到其对应的反向点x*，由透镜成像原理可得：

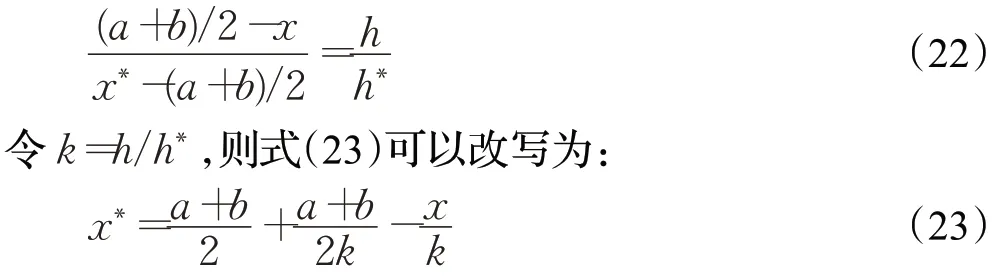
式（23）为透镜成像反向学习反向解的求解公式。若k=1，则式（23）可简化为：

式（24）即为文献[18]中一般反向学习反向解的求解公式。

显然，一般反向学习是透镜成像反向学习的一个特例。采用一般反向学习得到的反向解是固定的，而在透镜反向学习中通过调整k的大小，可以获得动态变化的反向解，进一步提高算法寻优精度。

将式（23）推广到D维优化问题中，得到基于透镜成像原理的反向学习公式如下：

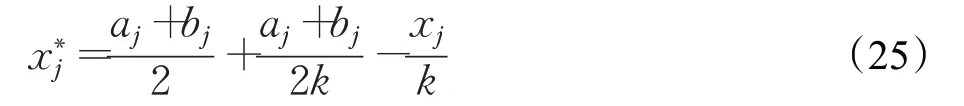
式中，a j和b j分别为搜索空间中第j维的最小值与最大值；x j为当前个体在第j维的分量，为x j的透镜反向解。

2.3.2 具备观测触发机制的透镜成像学习

HHO算法在迭代后期种群多样性降低，哈里斯鹰群体聚集在最优个体位置附近，当最优个体陷入局部最优时难以跳出局部极值空间区域，导致算法早熟，寻优精度下降。本文采用透镜成像学习策略对哈里斯鹰群体进行扰动，以增强种群多样性，提高算法跳出局部最优的可能性。

调节因子k是影响透镜成像学习性能的一个重要参数。考虑到较小的k值生成的反向解范围更大，而较大的k值能产生小范围内反向解，结合HHO算法迭代前期大范围探索及迭代后期局部精细搜索的特点，本文提出一种随迭代次数变化的调节因子：

其中，t为当前迭代次数，T为最大迭代次数。由于式（25）中k作为分母调节反向解，随着迭代次数增加，k值变大，透镜成像反向学习的反向解范围越来越小，这种调节方式增强了算法迭代后期局部位置的精细搜索。

每次迭代都对哈里斯鹰群体进行扰动会增加算法的运行成本。因此，本文嵌入一种基于迭代次数和最优适应度值的观测算子，来观测算法是否陷入局部最优，表达式如下：

通过透镜成像反向学习产生的反向解，不一定优于原始解。因此，引入贪婪选择策略，选择是否将原始解用反向解替代，即只有当反向解的适应度值更优时，才进行替换。公式如下：

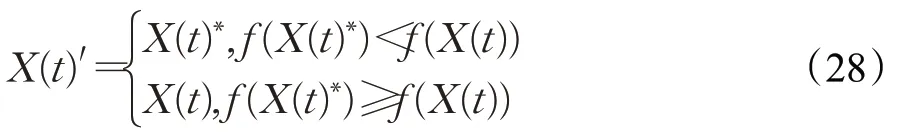
其中，X(t)*为反向解，X(t)′为贪婪选择后的哈里斯鹰位置。

当算法陷入局部最优时，通过观测触发算法产生透镜成像学习反向解，利用贪婪策略选择原始解与反向解中适应度更优的个体，从而生成位置更佳的哈里斯鹰群体，有效避免了迭代后期种群多样性下降，算法易早熟收敛的问题。

2.4 IHHO算法的伪代码

融合互利共生和透镜成像学习的哈里斯鹰优化算法描述如下：

算法1IHHO算法

2.5 IHHO的时间复杂度分析

时间复杂度是评价算法求解速度的一个重要指标。本文对改进后HHO算法进行时间复杂度分析。

在基本HHO算法中，假设种群规模为N，维数为d，最大迭代次数为T，根据时间复杂度的运算规则，可得基本HHO算法的时间复杂度为O(N×d×T)。对于IHHO，混沌初始化阶段的时间复杂度与HHO基本相同，探索阶段计算惯性权重w的时间复杂度为O(T)。在透镜成像学习扰动阶段，生成随机数rand(0,1)和计算观测算子β的时间复杂度为均为O(T)，判断随机数rand(0,1)与β大小的时间复杂度为O(T)，计算每只个体透镜成像反向解的时间复杂度为O(N×d×T)，贪婪比较个体适应度值的时间复杂度为O(N×T)。则IHHO的时间复杂度为O(N×d×T)。

可见，IHHO的时间复杂度与HHO相同，表示本文所提改进策略没有降低算法的求解效率。

3 算法性能测试

3.1 实验设计

基于16个基准测试函数，在MATLAB 2020a中，测试比较IHHO与5种新颖智能算法MFO[19]、GWO[20]、SCA[21]、WOA[22]、HHO的性能。测试环境为Windows10 64 bit操作系统，设置每种算法的种群规模均为30，最大迭代次数为500；为了降低随机性干扰，每种算法均独立运行30次。IHHO中w、k、β均按本文提出公式更新，其他算法参数与原文献一致。16个基准测试函数如表1所示，其中F1~F7为高维单峰函数，F8~F12为高维多峰函数，F13~F16为固定维度函数。

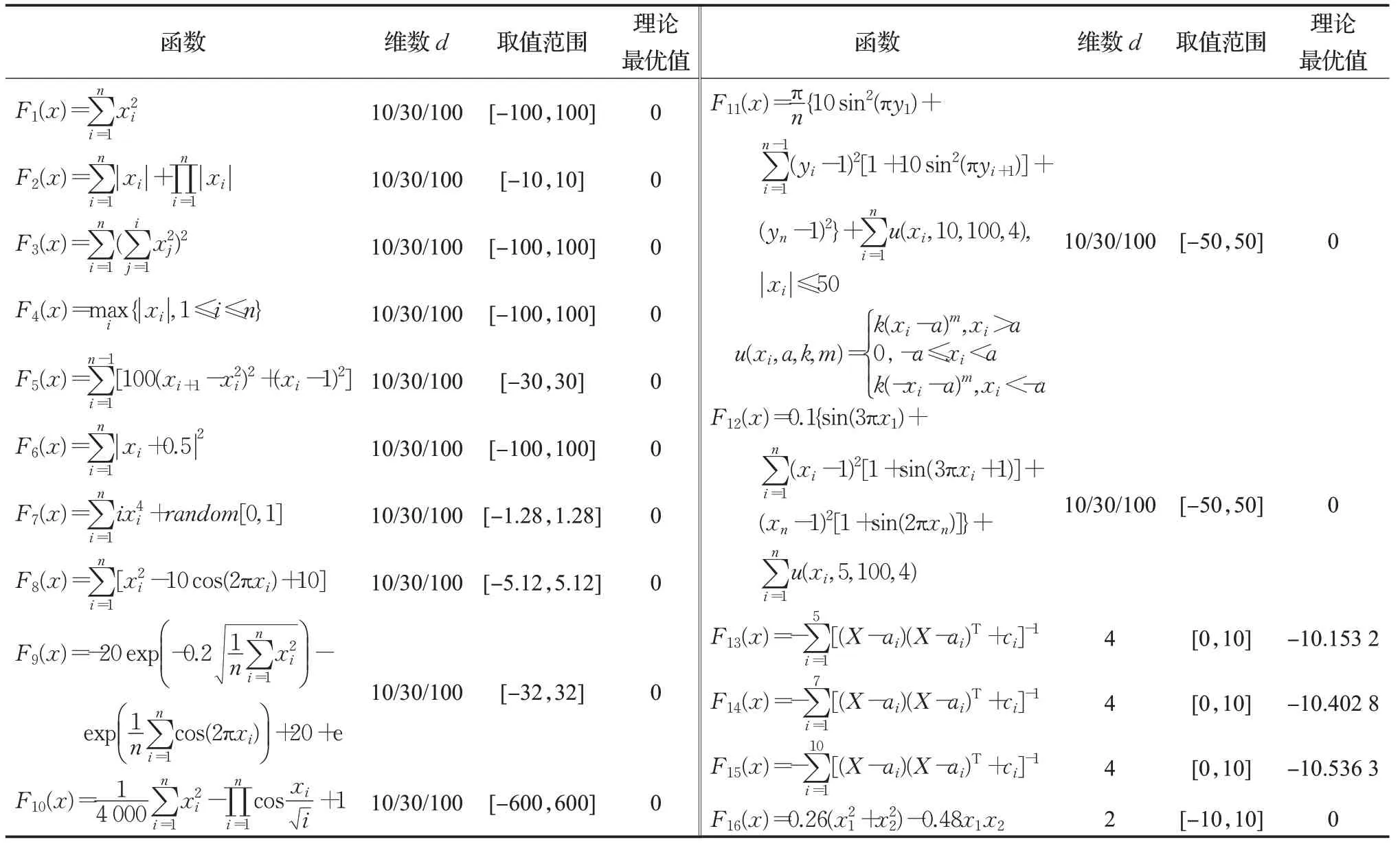
表1 基准测试函数Table 1 Benchmark functions

3.2 算法性能对比分析

6种算法优化12个高维测试函数(d=10/30/100)的实验结果如表2所示，4个固定维度测试函数实验结果如表3所示。

由表2可知，对于单峰函数F1、F2、F3、F4，不论在10维、30维还是100维下，IHHO的求解精度相较于其他5种算法均有了较大提升，且平均值均能达到理论最优解，标准差为0；在维数增大时HHO的寻优精度下降，而IHHO的求解精度基本不受影响。对于函数F5，大多数算法的求解精度都较低，而在30维和100维时，IHHO的寻优精度最高，说明本文改进策略能够增强算法跳出局部最优的能力。对于单峰函数F6，在30维和100维时，IHHO求解的平均值和标准差最小，而在10维时，IHHO的寻优精度略低于MFO，但相较于HHO有了较大的提升。对于单峰函数F7，IHHO在不同维度下的寻优结果最接近理论最优解，且标准差最小。对于多峰函数F8、F10，HHO和IHHO均能找到理论最优解，且标准差最小；对于多峰函数F9，HHO和IHHO的求解精度相同，且优于其他4种算法，说明HHO和IHHO对F8、F9、F10的寻优效果较好。对于多峰函数F11和F12，在不同维度下，IHHO的平均值和标准差均小于HHO和其他4种算法，改进后的HHO性能最佳。

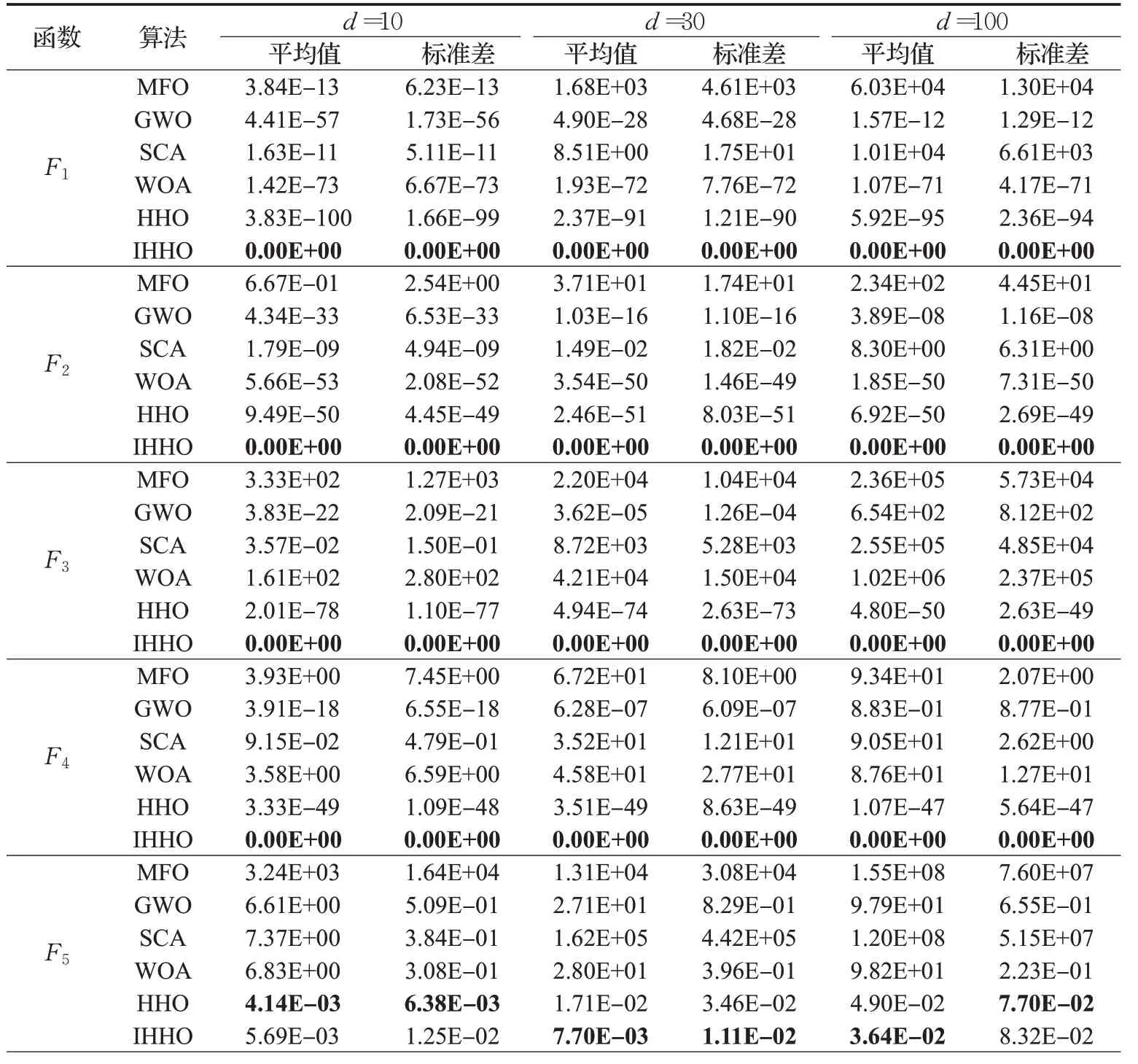
表2 高维测试函数优化结果Table 2 Optimization results of high dimensional test functions

由表3可知，对于固定维度函数F13、F14、F15，只有GWO和IHHO的寻优精度接近理论最优值，且IHHO相较于GWO的平均值更接近理论最优解；与基本HHO相比，IHHO的寻优性能有了较大的提升。对于固定维度函数F16，IHHO的求解精度与理论最优值相同，说明IHHO能够有效跳出局部最优，提升算法寻优精度。

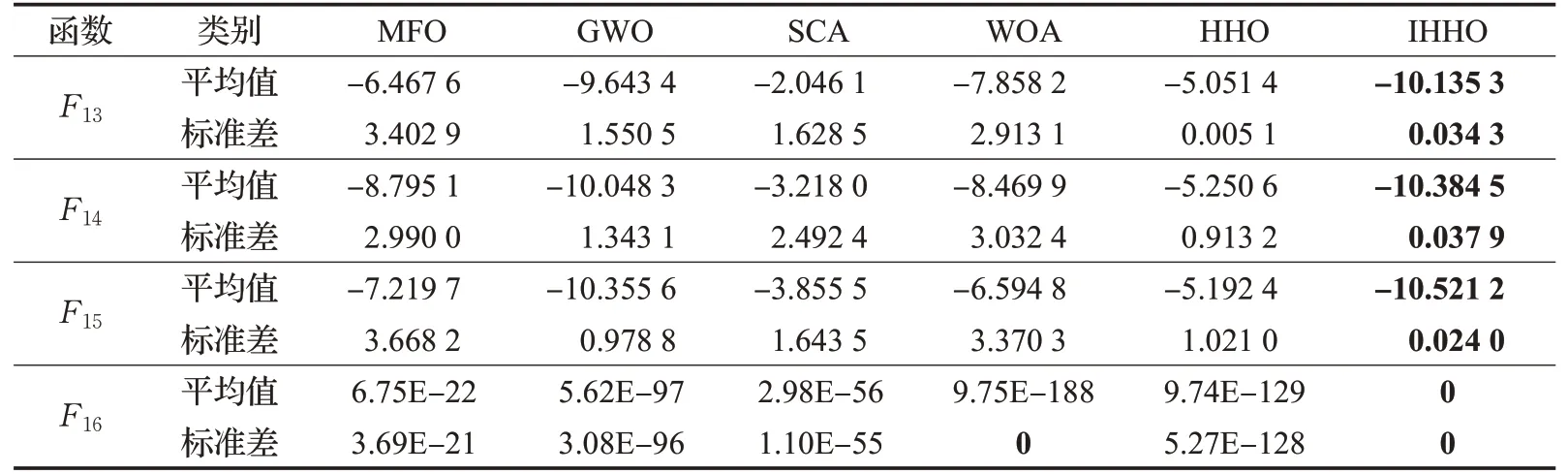
表3 固定维度测试函数优化结果Table 3 Optimization results of fixed dimension test functions

总体上看，IHHO在求解不同函数优化问题时，能够有效跳出局部最优，提高求解精度，表现出良好的寻优性能。

3.3 算法收敛曲线对比分析

6种算法优化12个高维测试函数(d=30)和3个固定维度测试函数的迭代收敛曲线如图5所示，图中横坐标为迭代次数，纵坐标为平均适应度值。

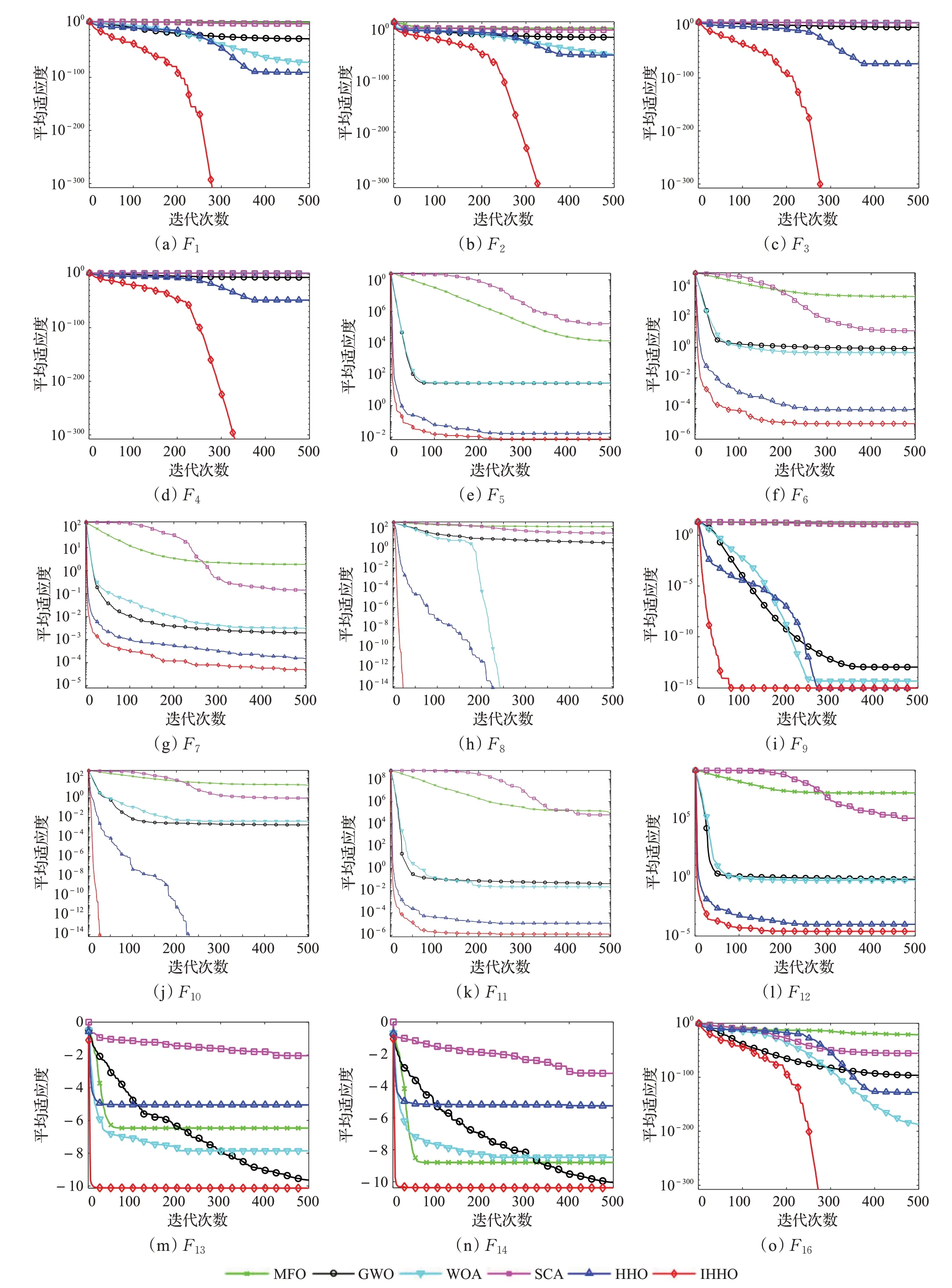
图5 测试函数迭代收敛曲线Fig.5 Test function iterative convergence curves

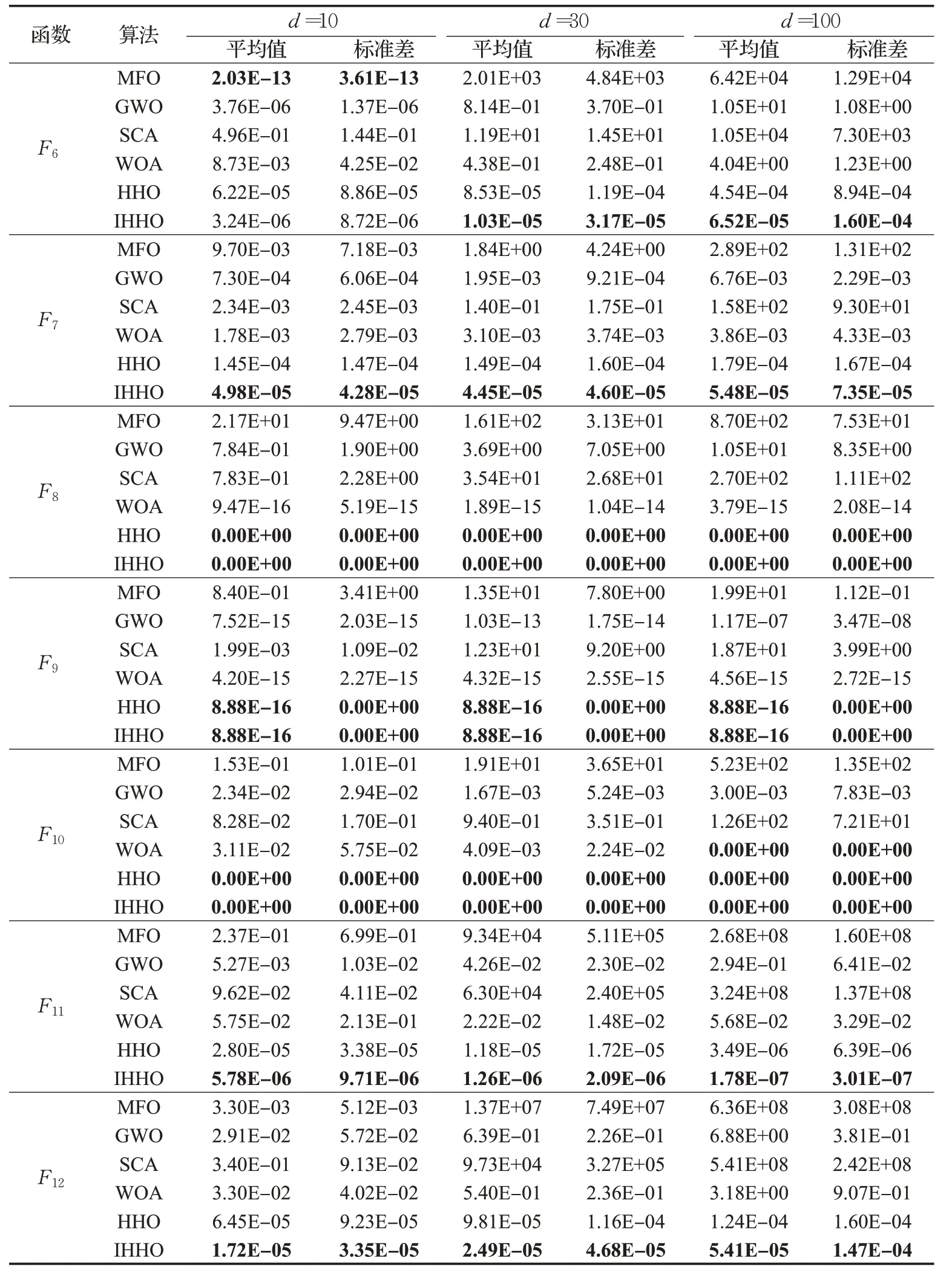
表2（续）

对于高维函数，从F1、F2、F3、F4的迭代曲线可知，在迭代前期w的值较大，种群迅速向中心聚集，收敛速度较快；在迭代200次左右曲线出现拐点，随着迭代次数增大，算法进行透镜成像学习的概率变大，适应度值迅速下降。由F5、F6、F7、F11、F12的迭代曲线可知，IHHO在迭代100次左右就达到了HHO的求解精度，此后由于透镜成像学习的扰动作用，促使算法跳出局部空间继续搜索。从F8、F9、F10的迭代曲线可以看出，IHHO在迭代100次之前就能收敛到最优精度，说明改进的探索阶段搜索策略提高了HHO的收敛速度。

对于固定维度函数，从F13、F14可知，IHHO在初始阶段的适应度值就优于其余5种算法，说明利用Tent混沌初始化的种群质量更高，在一定程度上提高了算法的全局搜索性能；同时从收敛速度上看，IHHO在迭代10次左右就出现拐点，具有更快的收敛速度。由F16的曲线也能得出，IHHO算法求解精度更高，收敛速度更快。

综上而言，改进后的哈里斯鹰优化算法性能提升较大，是一种更为高效的算法。

3.4 改进策略的有效性验证

本文融入了3种策略改进HHO算法，为了验证本文改进策略的有效性，对比SOCHHO（只引进本文2.1节Tent混沌初始化和2.2节互利共生思想）、LIHHO（只引进本文2.3节中透镜成像学习策略）和IHHO在优化部分典型测试函数时的性能。参数设置与3.1节相同，3种算法独立运行30次，测试结果如表4所示。

从表4中可知，融入3种策略改进的IHHO算法寻优精度（平均值）和稳定性（标准差）均优于SOCHHO和LIHHO。对于函数F1、F2、F3，IHHO均能够求得最优解，且标准差为0；采用透镜成像学习的LIHHO算法寻优精度要优于SOCHHO算法。对于函数F11、F12，IHHO的寻优精度高于LIHHO算法和SOCHHO算法。对于函数F13、F14、F15，IHHO的求解结果比SOCHHO算法和LIHHO算法更接近理论最优值。图6显示了F1、F3、F14收敛曲线图，从图中可知，融入透镜成像学习的LIHHO算法的寻优精度和收敛速度要优于融入Tent混沌初始化和互利共生策略的SOCHHO算法，而融入本文3种策略改进的IHHO算法在寻优精度和收敛速度上均优于SOCHHO和LIHHO算法。说明本文所提透镜成像学习策略相较于其他两种策略对HHO算法性能的提升更大，3种策略的相互配合使得改进后的IHHO算法性能更加优秀。

图6 迭代收敛曲线Fig.6 Iterative convergence curves

3.5 与一般反向学习策略对比分析

本文提出的透镜成像学习策略是在一般反向学习的基础上进行改进的。为了证明本文透镜成像学习的优越性，将一般反向学习（调节因子k=1）替代本文2.3节透镜成像学习，并融入本文2.1节和2.2节的改进策略，得到一种新的改进HHO算法（OBLHHO）。在典型测试函数中，测试比较OBLHHO与IHHO的性能，两种算法均独立运行30次，得到实验结果如表5所示。

从表5中结果可知，与OBLHHO算法相比，IHHO算法在7个测试函数上均获得了明显优势；OBLHHO算法仅在F11上的测试结果稍优于IHHO。这表明，融入透镜成像学习的改进HHO算法在优化不同函数问题时的适应性更强，具备动态调节因子的反向学习使得哈里斯鹰群体在迭代后期不失种群多样性，能够跳出局部极值空间，提高寻优精度。

表5 OBLHHO与IHHO的测试结果对比Table 5 Comparison of test results between OBLHHO and IHHO

4 IHHO算法在图像分割中的应用

图像分割就是将图像中具有特殊意义的不同区域提取出来的过程。在计算机视觉中，目标识别、特征提取都依赖于图像分割的质量。常见的图像分割方法有阈值分割法、区域生长分割和聚类法等。为了验证IHHO算法在实际工程应用中的可行性，本文将IHHO应用到图像分割问题中。

最大熵分割法是一种广受关注的阈值分割法，图像信息量越大，熵就越大，最大熵就是找出一组最佳阈值使得总熵值最大[23]。传统阈值分割法采用穷尽搜索方式进行图像多阈值分割，计算时间长，分割精度低。本文采用IHHO算法进行图像多阈值分割，选择最大熵作为目标函数来搜索阈值，即寻找一组解(t0,t1,…,t n)使得目标函数值最大。相应的目标函数如下：

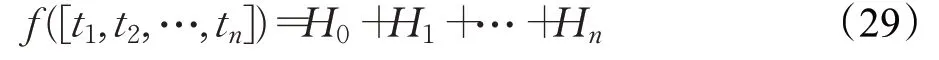
其中，H为图像各部分熵值。

设置种群数量为30，最大迭代次数为100，选取Lena、Barbara、Peppers、Cameraman、Baboon作为测试图像，仿真对比HHO算法和IHHO算法的阈值分割效果。为了降低偶然性，每幅图像分别进行20次阈值分割，得到分割结果如表6所示。

由表6可知，采用IHHO算法对图像进行不同阈值分割时，得到的总熵值均高于HHO，且标准差小于HHO。说明IHHO算法的分割精度更高，稳定性更强。

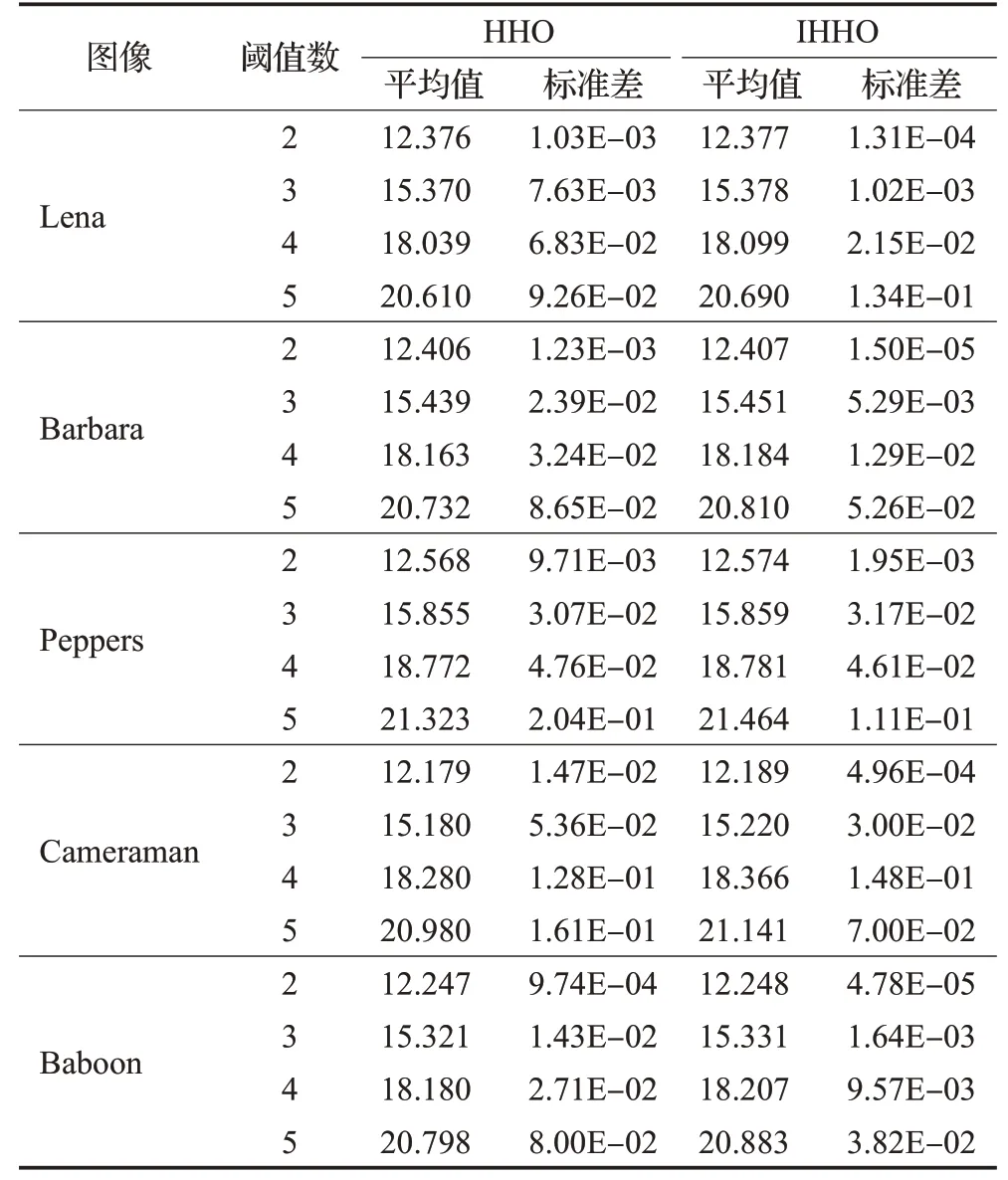
表6 测试图像多阈值分割结果Table 6 Multithreshold segmentation results of test images

为了直观显示两种算法的分割效果，图7给出了两种算法对各图像的5阈值分割图。从图中可知，IHHO分割后的图像比HHO分割后细节更清晰，信息更完整，分割效果更佳，验证了本文算法应用到实际工程问题中的可行性。

图7 测试图像5阈值分割结果对比Fig.7 Comparison of 5 threshold segmentation results of test images

5 结束语

针对基本哈里斯鹰优化算法的缺陷，本文提出融合互利共生和透镜成像学习的哈里斯鹰优化算法（IHHO）。基于16个基准测试函数进行仿真实验，比较算法性能，并将IHHO算法应用于图像分割中，得出以下结论：

（1）IHHO的寻优性能提升明显。利用Tent混沌初始化哈里斯鹰种群，丰富了种群多样性，改善了算法全局搜索能力；融合互利共生思想以及惯性权重，有效平衡了算法的全局探索及局部开发能力；引入透镜反向学习策略，提高了算法跳出局部最优的能力。

（2）16个基准测试函数的实验结果表明，IHHO相较 于MFO、GWO、SCA、WOA、HHO、SOHHO以 及OBLHHO的收敛速度更快，求解精度更高，跳出局部最优的能力更强，证明了本文改进策略的有效性。同时，IHHO在图像分割中的表现比HHO更佳，验证了IHHO应用在实际工程问题中的可行性。

下一步可以考虑改进哈里斯鹰算法结构，融合其他智能算法优点，进一步提升算法性能，并将该算法应用到更多实际优化问题中。