多尺度特征融合的光伏电站故障诊断

那峙雄，孙 涛，来广志，王 栋，张长志

1.国网电子商务有限公司，北京 100053 2.国网天津市电力公司 电力科学研究院，天津 300220

太阳能是一种清洁、可再生的能源，在我国新能源发展战略中占有重要地位，而光伏发电是目前利用太阳能最广泛、最有效的方式。分布式光伏电站是光伏发电的一种基础设施，特指在用户场地附近建设，运行方式为用户侧自发自用、多余电量上网的光伏发电设施。分布式光伏电站能够有效缓解局部用电紧张的状况，并且满足无噪声、无污染的要求。但随着分布式光伏发电设备部署规模的发展，其运维难度也显著增大。以某分布式光伏发电站为例，该电站年发电量约为220万千瓦时，光伏设备众多，设备位置分散，所处环境多变，对其进行人工巡检效率低，成本高，出现故障后难以及时发现，严重影响光伏电站的正常运行。因此，自动化的光伏设备故障诊断算法具有极高的研究和应用价值。

目前的故障诊断算法可以分为基于设备电气特性和基于机器学习两大类。基于设备电气特性的算法依赖于特定的、准确的电气数据进行数学建模，而获得这些数据需要复杂的硬件支持以及人力维护，因此难以在实际生产中广泛应用。基于机器学习的诊断算法能够从不同类型的输入数据中挖掘故障设备的特征，并且能够容忍数据输入的噪声。但是目前的故障诊断算法研究都采用了设备之间没有差异、不同日期的天气条件没有差异的假设。这个假设只适用于集中式光伏电站，而分布式光伏电站中，设备的设置地点、放置角度、投入使用时间等都存在着较大差异。另外，已有的机器学习算法往往只能利用交流电流、交流电压、直流电流、直流电压四项数据，而实际监测数据中往往包含十多项条目，其中蕴含大量信息可以挖掘利用。

针对已有算法的问题，本文首先提出了一种矫正设备因素差异、天气条件差异的数据规范化方法。通过同一日期内所有设备的运行情况衡量当天的天气条件，计算天气条件矫正因子；通过同一设备的历史运行情况衡量该设备的健康状况，计算设备矫正因子。借助这两个矫正因子，将监测数据的绝对数值转化为相对数值，从而减弱设备、天气差异对故障诊断的影响。在此基础上，本文提出了一种基于多尺度时序特征的故障诊断深度学习模型。首先，针对分布式光伏电站监测数据数值波动大、噪点多的数据特点，模型通过多尺度邻域特征提取单元实现平滑输入、消除噪点的效果，同时又避免了平滑过度、信息丢失的问题；然后，使用带有注意力机制的长短时记忆单元（long short-term memory，LSTM）[1]提取序列特征，以应对监测数据序列长、维度高的特点；最后，使用度量学习的方法训练模型，增强模型的辨别能力，提高对难样本的诊断效果。

本文的研究成果可以概括为以下三点：

（1）针对分布式光伏电站设备差异较大、天气条件差异较大的问题，提出了一种矫正差异的数据规范化方法。

（2）针对分布式光伏电站监测数据数值波动大、噪点多的特点，提出了融合多时序尺度特征的故障诊断模型。

（3）针对分布式光伏电站故障样本数量不均衡的问题，迁移使用了一种度量学习的损失函数进行辅助训练，进一步提升模型辨别能力。

本文在某分布式光伏电站的实际监测数据上对提出的数据规范化算法、故障诊断模型进行了实验，证明了其在实际应用场景下的有效性。

1 相关工作

1.1 光伏设备故障诊断算法

光伏设备的I-V曲线体现了光伏设备的输出特性，能够反映设备的故障情况[2-3]，是经常用于故障诊断的电气特性。Liu[4]和Ding等[5]对热斑组件I-V曲线进行建模，借助曲线的特征对光伏阵列健康状态进行定量评估。Liu等[6]提出等效电路法，利用伏安特性进行故障诊断，通过光伏阵列等效电路模型中串联等效电路来判断系统中是否存在故障组件。由于实际应用场景中难以获得精确的I-V曲线，这类算法很难达到理想的效果。

光伏电站不间断产生的大量监测数据为基于机器学习和深度学习的故障诊断算法提供了很好的支持。Lin等[7]和Ye等[8]分别采用支持向量机和级联随机森林模型对监测数据进行分类来实现故障诊断。Zhu[9]和Lu[10]将聚类算法应用到光伏故障检测上，先将光伏设备根据其环境特征进行聚类，然后比较同一类中的设备，从而筛选出故障设备。除了传统机器学习算法外，深度学习模型也被应用到该领域内。Zhang等[11]采用卷积神经网络（convolutional neural network，CNN）和双向门控循环单元（bidirectional gate recurrent unit，biGRU）的双分支结构处理电站监测数据，双分支各自提取不同的特征，最后拼接形成整体特征用于故障检测。Wu等[12]使用经验模态分解算法和CNN对时间序列进行分类，从而得到诊断结果。基于机器学习和深度学习的故障检测算法不需要对设备电气特性进行分析，可以直接作用在监测数据上并产生诊断结果，有较强的抗干扰能力。

1.2 时序特征提取

传统的时序特征提取算法主要是通过分析时序数据的波形来提取特征。Baydogan等[13]提出了时间序列特征包（time series bag of features，TSBF）算法，使用特征袋（bag of features，BoF）集成来自时间序列各部分的局部信息，将各个序列片段的特征组成整个时序数据的特征包。Keogh等[14]提出了Shaplets的概念，仅将时间序列中最易区分的特征提取出来，拼接形成序列特征，从而减弱噪声的干扰。基于Shaplets的算法大都没有考虑更高维度的特征，因此在处理长序列或多维数的数据时效果都不尽人意。

循环神经网络（recurrent neural network，RNN）是常见的处理序列数据的深度学习模型，而LSTM是RNN的一个变种，其门控机制能够有效避免RNN在处理长序列输入时的梯度消失或梯度爆炸的问题。在循环神经网络的基础上，Sutskever等[15]提出了编码器-解码器（encoder-decoder）模型，实现了序列输入到序列输出的转换；Bahdanau等[16]提出了注意力机制来解决编码器和解码器之间的信息损失问题，使得网络能够自适应地关注序列的局部信息。

1.3 度量学习方法

度量学习（metric learning）是样本特征之间的距离学习，目标是同类样本的特征尽可能相似，而类间的特征距离尽可能远。Liu[17]、Wang[18]、Deng[19]等的一些系列研究将全连接层权重视作各个类别的中心特征，从而将softmax分类损失转化为特征向量与中心特征之间余弦距离损失。Song等[20]将行人重识别问题视为行人特征差向量的二分类问题，并采用马氏距离优化样本特征的相似性。

除了直接优化距离损失函数的方式外，还可以通过正负样本对比的方式实现度量学习。Hadsell等[21]设计了对比损失函数，通过欧式距离优化所得特征。Schroff等[22]提出了三元组损失函数，在网络的每次迭代中选择一组同类样本、一组异类样本进行训练，从而提升度量学习的效率。Feng等[23]在三元组损失函数的基础上，为正样本之间的距离设置了阈值，训练时过滤掉低于阈值的样本，从而避免了过小的类内距离导致网络收敛缓慢的问题。

2 基于多尺度时序特征的故障检测算法

2.1 光伏电站监测数据规范化算法

受设备投入使用时间、所处位置等因素的影响，即使在相同的天气条件下，两组正常运行的设备都可能产生不同的数据，如图1所示。由于天气变化、季节更替的影响，即使相同的设备，在不同日期正常运行时产生的数据也可能不同，如图2所示。

图1 不同设备同一日期的交流功率曲线Fig.1 AC power curve of different equipments on same date

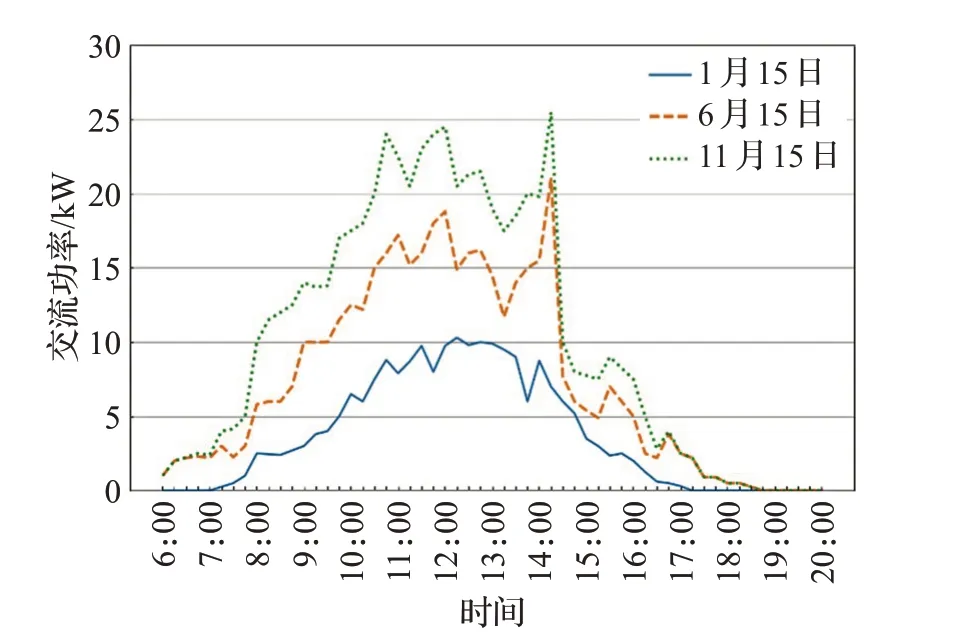
图2 同一设备不同日期的交流功率曲线Fig.2 AC power curve of same equipment on different dates

这种现象会给故障诊断带来很大的困难。设备安装位置较差、投入使用时间较长或者当天的天气条件较差都会造成较低发电量，但这些情况不应当被诊断为设备故障。相反，一台设备某天的发电量监测数据在正常范围内，但其可能仍发生了故障，只是其安装位置、天气条件较为优越，即使存在故障，仍可以达到发电量的平均水平。因此，仅仅根据单独一台设备在某个日期产生的监测数据对其进行诊断很容易造成误判。

针对这个问题，本文设计了一种可以消除不同设备、不同天气等差异带来的影响的数据规范化算法，其流程如图3所示。该算法利用设备之间的横向对比矫正设备差异，利用日期之间的纵向对比矫正天气因素差异，从而消除设备、天气等因素的影响。算法将同一设备不同日期的监测数据平均值作为日期矫正因子，将不同设备同一日期的监测数据平均值作为设备校正因子。通过计算实际监测数据与这两个校正因子的比值关系，将监测数据转化为相对数值。该相对数值是设备之间对比、日期之间对比的量化结果，从而修正了监测数据中设备差异、天气差异等因素带来的固有偏差。

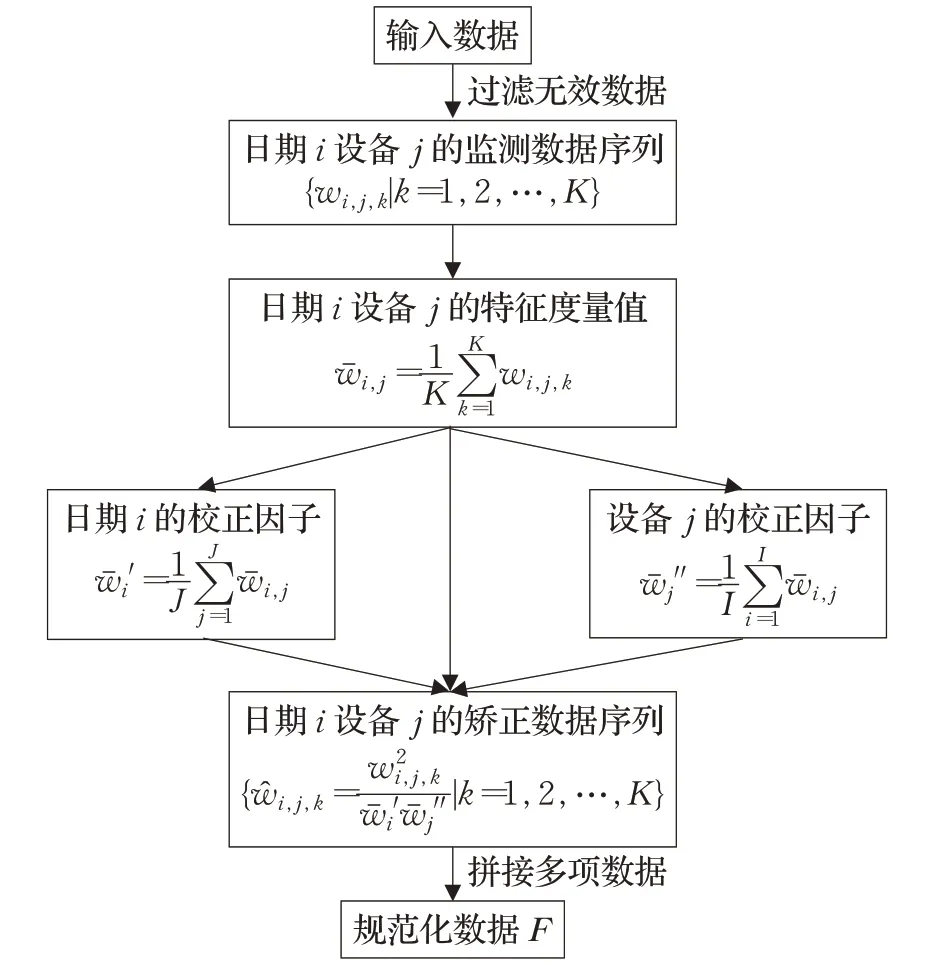
图3 数据规范化算法流程Fig.3 Data normalization algorithm workflow

以发电量这一项数据为例来说明，用wi,j,k表示第i天第j组设备在当天第k个时刻监测到的发电量数据。计算当天各个时刻发电量的平均值wˉi,j来衡量第i天第j组设备的发电量水平，即：其中，K表示每天记录数据的时刻数。这个数值是同时受设备因素和天气条件因素干扰的，需要综合设备历史运行情况和其他设备当天运行情况对其矫正。用第i天中所有设备发电量的平均值′作为日期因素的矫正因子，用第j组设备在所有日期下发电量的平均值作为设备因素的矫正因子，即：

其中，I表示有数据记录的日期数，J表示设备数。通过这两个矫正因子，可以计算不受日期差异和设备差异影响的时序数据即：

对其他数据项也做相同的处理，随后拼接起来形成二维张量F∈RK×N，其中N表示所有数据项维度之和。

本方法并没有从局部的数值特征入手，而是将设备固有的发电水平、不同日期的发电条件等因素考虑进来，通过横、纵向对比的方法，将各项监控数据转化为相对数值关系，从而使得监测数据中的异常更容易被分析挖掘。在转化为相对数值的过程中，可能存在少量信息的损失，对整个诊断系统的灵敏性造成影响。但实际监测数据包含的项目众多且采样频繁，一定程度的信息损失并不会对诊断系统造成太大的干扰。

2.2 故障诊断网络

总体上，本模型采用多尺度特征提取模块辅助LSTM提取序列特征的设计，整体结构如图4所示。多尺度卷积能够通过不同尺度邻域内的加权求和运算平滑输入，过滤噪点，从而降低后续网络的学习难度。而带有注意力机制的LSTM可以处理长序列、高维度的输入数据，能够提取出时序数据中的特征。网络的训练过程中，除了常规的分类监督，还使用了度量学习的损失函数，从而进一步增强模型的辨别能力，提升其对难样本的诊断效果。

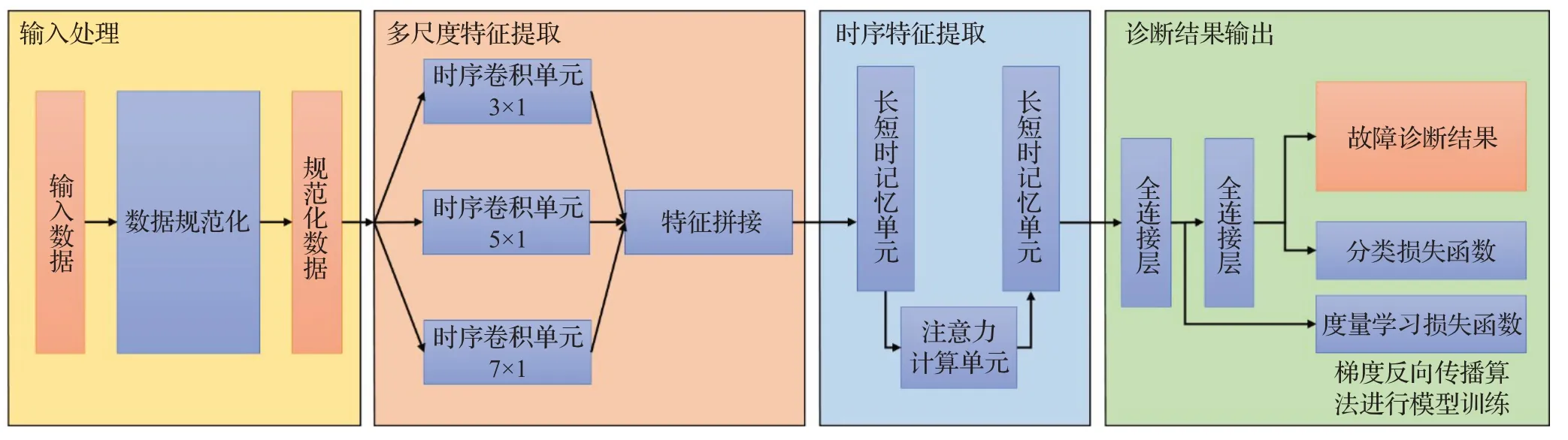
图4 融合多尺度时序特征的故障检测算法流程Fig.4 Workflow of fault diagnosis algorithm based on multi-scale time serial features fusion

2.2.1 多尺度邻域特征提取模块

卷积神经网络最初是应用在图像领域中的模型，但其局部特征提取的思想同样可以应用到时序数据分析中。一个卷积核大小为3的时序卷积结构如图5所示，对于时序数据输入，卷积核以滑动窗口的形式沿时间维度移动，并输出每个时序片段内数据的加权和。每个卷积单元堆叠了多个卷积核从而输出多维特征。大卷积核会从大尺度时序邻域内提取特征，其中邻域内每项数值产生的影响更小，从而减弱输入数据的波动，减轻其中噪点对输出特征的影响。但大尺度卷积核减弱了数值变化的差异，容易导致平滑过度的问题，使得输出特征失去判别能力。与之相对的，小尺度卷积核能够较好地保留输入数据中的信息，但是也更容易受到其中噪点的干扰。考虑到不同尺度卷积的特点，组合使用不同大小的卷积单元提取不同时序尺度的特征。然后采用特征拼接的方式完成特征融合，从而得到多尺度邻域特征。通过这种方式，输出的特征既包含了平滑后的特征，也保存了原始输入的特征。在模型的训练过程中，后续的网络结构可以学习分析这两种特征，从而在一定程度上实现了平滑输入数据并且避免信息丢失。

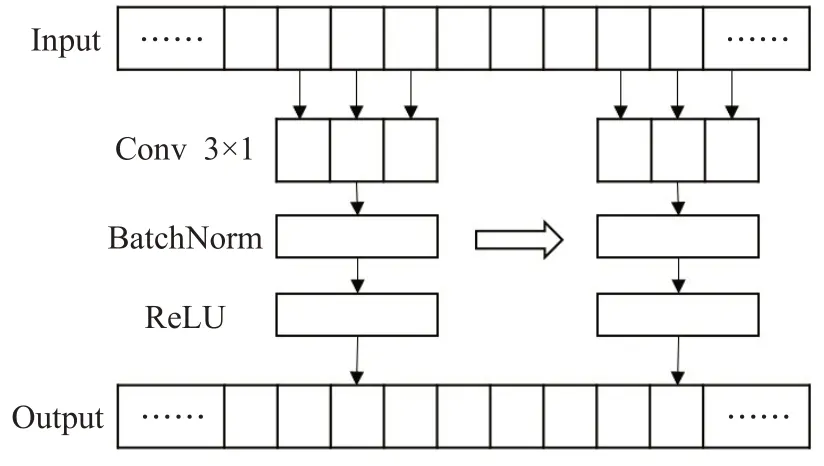
图5 时序卷积单元Fig.5 Time series convolution unit

本文使用卷积核分别为3、5、7的三种时序卷积组成多尺度时序特征提取单元。时序卷积C由卷积层、批归一化层（batch normalization，BN）、修正线性单元（rectified linear unit，ReLU）组成，其运算可以表示为：

其中，x和h分别表示时序卷积单元的输入和输出；W和b分别表示卷积核内可训练的权重和偏移；⊗表示卷积操作；BN(·)表示批归一化层，能够使网络训练更加稳定、迅速；ReLU(·)表示激活函数，使得模型能够拟合非线性映射，同时避免梯度消失的问题。多尺度时序特征提取单元M可表示为：

其中，C1×k表示卷积核为1×k的卷积单元，x和y分别表示输入和输出。cat(·)表示特征拼接操作，即将维数分别为d1、d2和d3的向量，拼接成d1+d2+d3维的向量。将特征直接相加或使用最大池化也可以实现特征融合，但这两种方式都会带来信息损失。

2.2.2 时间特征提取模块

光伏电站监测数据有序列长、维度高的特点，因此时间特征提取模块需要具备较强的表征能力和特征提取能力。为此，本模型采用了两层LSTM组成的“编码器-解码器”（encoder-decoder）结构来实现，可表示如下：

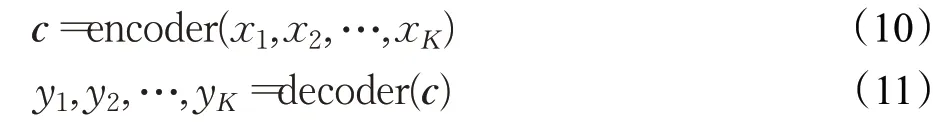
其中，x1,x2,…,x K和y1,y2,…,y K分别表示时间特征提取模块的输入与输出；K表示序列长度；c表示编码器最后一次迭代的输出向量。从上式中可以看出，编码器到解码器之间的信息传递都通过向量c实现，其中不可避免地存在信息损失。

为了解决这个问题，在二者之间增加了注意力机制，从而由网络自主学习哪部分信息可以丢弃，哪部分信息需要关注。添加注意力机制的网络结构可以描述为：

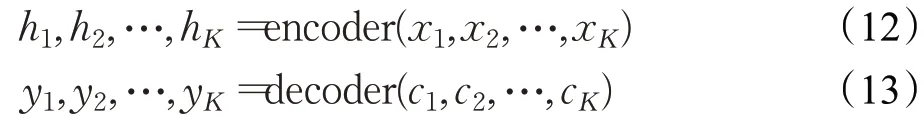
其中，h i表示编码器第i次迭代的输出；ci表示第i次迭代的上下文信息，其计算方式为：

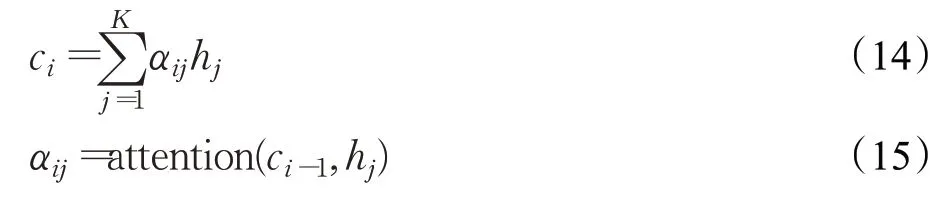
其中，attention()表示注意力机制网络，由一层全连接网络实现；αij表示第i次迭代时h j的权重；计算c1时使用零向量作为c0。

2.2.3 损失函数

最后的特征分类由两层全连接网络实现，接收LSTM最后一次迭代的输出向量，经线性运算后得到一个P+1维的向量y，其中P表示故障类别数。在进行诊断时，向量y通过softmax函数后得到预测q，其每一维可作为对应类别的概率，其中概率最大的类别作为最终的诊断结果。在进行训练时，使用了度量学习和分类监督两种损失函数，分别作用在第一、二层全连接网络的输出上，如图4所示。

分类监督使用的是加权交叉熵损失函数。因为实际应用中的监测数据往往存在类别不均衡的问题，即大部分样本都是正常运行时的监测数据，只有少部分是故障样本。如果使用一般的交叉熵损失函数进行训练，模型会忽略故障样本，倾向于将所有样本都诊断为正常样本，这样模型也可以取得较高的诊断准确率，但存在故障诊断召回率低的问题。所以需要对不同类别的损失进行加权，给数量较少的故障样本设置较高的权重。权重的计算方式为：

其中，wl表示类别l的权重；nl表示类别l的样本总数。则用于训练的加权交叉熵损失可表示为：

其中，M表示训练样本总数；p i表示样本的标签，即样本i属于第pi类故障状态；y(i)表示第i个样本输入时模型最后一层全连接层的输出，表示取向量y(i)的第j项数值。

模型的度量学习监督是将ArcFace损失函数迁移到故障检测任务上实现的。首先为各个故障类别维护中心特征矩阵W∈R(P+1)×D，其中D表示中心特征的维数。然后将常规的交叉熵损失函数拆解成样本特征f与中心特征的向量积的形式：

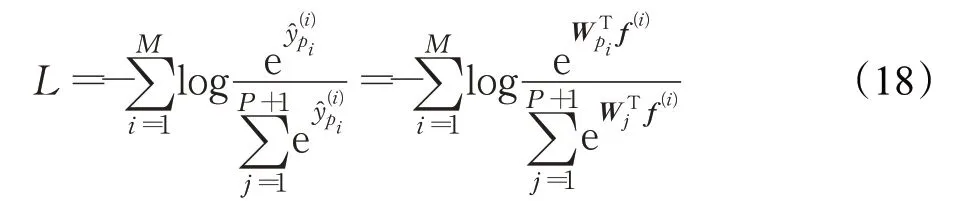
其中，p i表示样本的标签；W j表示第j类的中心特征；f(i)表示第i个样本的特征，在本模型中即为第一层全连接层的输出向量。又因为向量余弦距离可以定义为：

当固定中心特征W的模长为1，样本特征f的模长为s时，交叉熵损失可以进一步转换为：

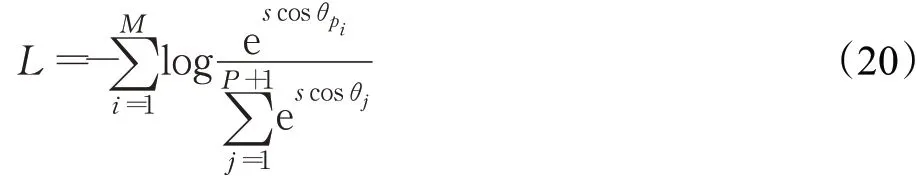
在这个形式下，交叉熵损失函数可以视作中心特征和样本特征夹角的损失函数。为了着重优化这个角度，增加对其的惩罚项m，最终度量学习的损失函数形式为：

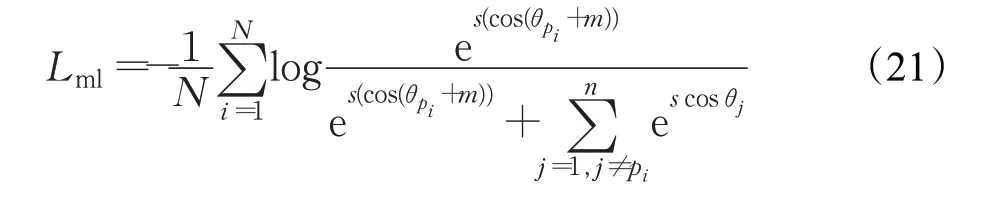
最终用于训练模型的损失函数Lfinal为：

其中，λ是度量损失函数的权重，实验中设置为0.5，表示以分类损失为主，度量学习起辅助作用。

2.2.4 模型训练设置

网络训练采用Adam优化算法[24]，如算法1所示。该算法使用滑动平均的方式估计梯度的一阶矩m和二阶矩v。然后将梯度的一阶矩视作动量，减弱了鞍点对训练的影响；将梯度的二阶矩作为梯度的修正因子，增强优化的稳定性。模型训练的初始学习率为0.001，训练共进行20周次，分别在第10、15周次将学习率衰减为原来的1/10。

3 实验验证

3.1 实验数据集

实验所使用的数据集来自某分布式光伏发电站2018年的监测数据。其中有效数据包含了352天内对34个设备组串的发电量、温度、交流端数据、直流端数据的记录，具体的数据项如表1所示。各项数据不间断地每15 min记录一次，但在没有阳光的时段中，监测数据没有实际意义且存在大量缺失，因此这里只采用了5：00到21：00之间的64次记录。

表1 监测数据项目说明Table 1 Monitoring data description

常见的光伏设备故障可分为四类，分别是光伏板遮挡故障、逆变器运行故障、逆变器短路故障和电压数值异常故障，这也是实验中进行诊断的故障类别。光伏板遮挡故障是由于杂物遮挡光伏板，导致光照面积减小，表现为逆变器电流明显减小；逆变器运行故障往往表现为输出端三相不平衡、电流异常或者电压较大；逆变器短路故障一般会导致输出端交流电流显著增大；电压数值异常故障表现为输出端三相阻抗数值异常，导致三相电压偏高。在实验数据集中，四种类别的故障样本以及正常样本数量如表2所示。实验中随机地将这些样本按照4∶1的比例划分成训练集和测试集。

表2 各类别样本数量Table 2 Number of samples in each category

3.2 实验环境及评估指标

实验基础硬件平台为一台搭载了Intel Xeon E5处理器、Nvidia GTX 1080ti显卡的服务器。采用Pytorch深度学习框架实现本文提出的模型（以下简称Multi-Conv+LSTM）。

实验中使用故障诊断准确率（accuracy）作为主要的评估指标，即诊断正确的样本占全部测试样本的比率。为了更全面地说明MultiConv+LSTM模型的诊断效果，还使用了精确率（precision）、召回率（recall）以及F1得分三个更精细的评估指标。这三个评估指标的定义是由二分类任务拓展而来的。考虑多分类任务中的一个类别，将属于该类别的样本称为正样本，不属于该类别的样本称为负样本。再将被预测正确的正样本数量记为TP（true positive），被预测正确的负样本数量记为TN（true negative），被预测错误的正样本数量记为FN（false negative），被预测错误的负样本数量记为FP（false positive）。在此基础上，以上评估指标可用下式进行计算：

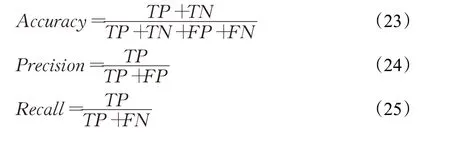
3.3 实验结果分析

3.3.1 数据规范化算法对比

在实验过程中，分别在原始数据和规范化后的数据上训练了MultiConv+LSTM模型，实验结果如表3所示。可以看出使用数据规范化后，故障诊断准确率有了大幅提升。在原始数据上，单条记录的数值大小对于故障诊断没有意义，模型只能挖掘出三相不平衡、直流串间不平衡这类症状，而漏检、错检大量样本。数据规范化算法将绝对数值转换为相对大小，使模型可以利用数据的绝对数值大小进行故障诊断。

将检测数据转化为相对数值的做法能够使异常数据更明显地暴露出来，也能够降低数据对于天气、设备差异等因素的敏感性。图6展示了数据集中两个逆变器五月份每天平均交流功率的原始数据和矫正后数据。逆变器1在5月24日产生故障，交流功率明显下降。但在原始数据上，其数值大小仍然与逆变器2接近，这导致模型无法诊断出逆变器1发生了故障；而在矫正后的数据上，通过设备矫正因子的影响，逆变器1交流功率的下降十分明显地表现出来，从而易于模型进行诊断。另外，5月5日到5月9日，两台逆变器的发电量都相对较低，从单个逆变器发电量上看，容易将其误判为发生了故障。但同时考虑这两台逆变器的数据，就能发现这段时间的低发电量更有可能是天气原因导致的。通过算法矫正后，数据在这段时间的波动被平滑到了相对较小的范围内，能够明显地与异常数据的波动区别开。因此，提出的矫正算法能够有效降低故障诊断对无关条件的敏感性，从而增强诊断效果的稳定性。

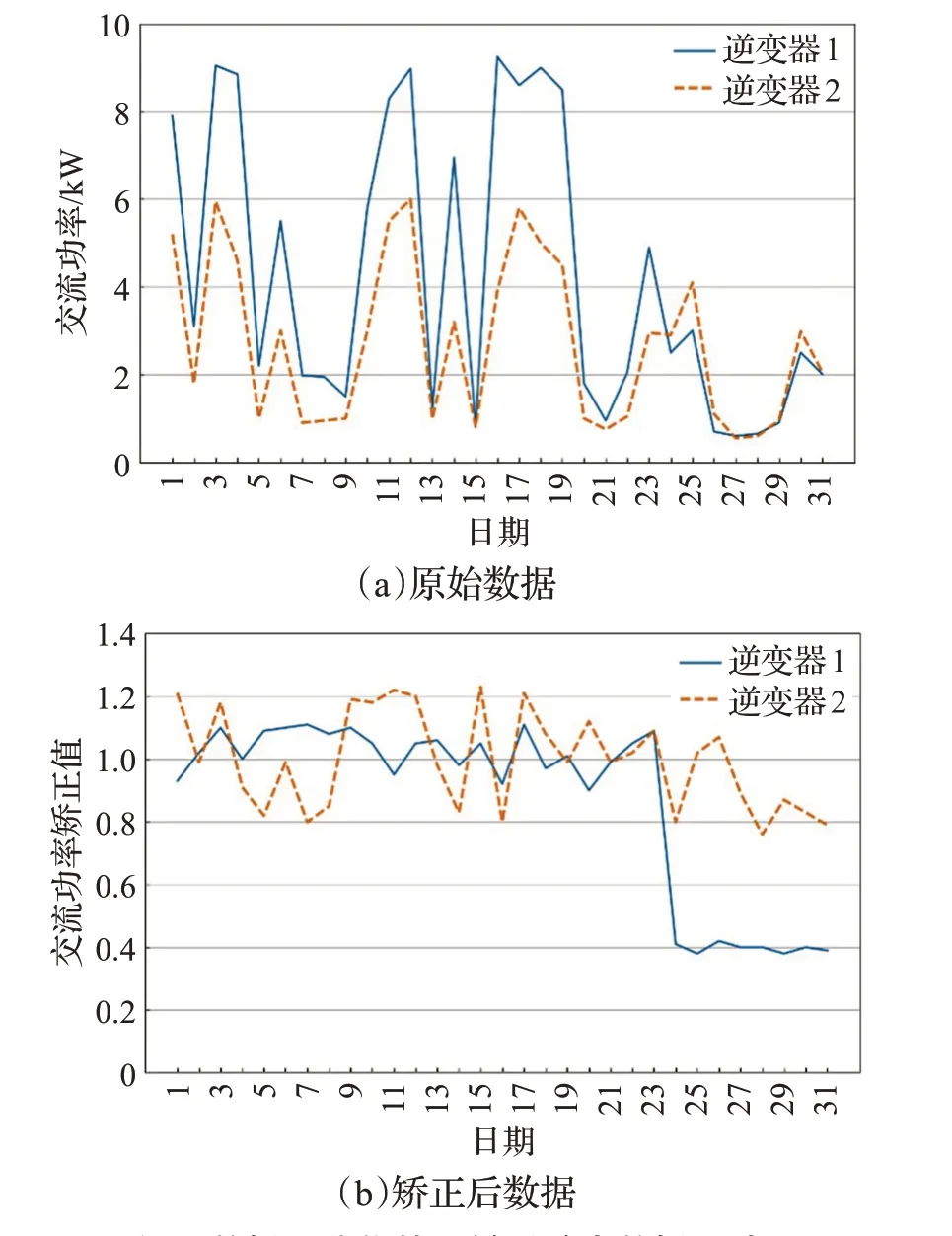
图6 数据规范化算法暴露异常数据的效果Fig.6 Effect of exposing abnormal data of data normalization method

3.3.2 时序分析算法对比

在规范化后的数据集上对传统算法LearningShapelet算法[25]、K最近邻算法（K-nearest neighbors，KNN），以及深度学习算法LSTM模型、全卷积神经网络（fully convolution network，FCN）模型[26-27]和biGRU+CNN进行了实验。为了保证对比的公平性，所有深度学习方法都使用相同的训练设置，只使用加权交叉熵函数作为损失函数。

在本实验中，所有算法都在规范化后的数据上进行训练和测试。表4对比了MultiConv+LSTM与其他时序数据分析算法的故障诊断准确率。可以看出深度学习算法整体领先于传统算法，可以体现出深度学习算法在有大规模数据支持时的优越性。在深度学习算法中，LSTM和FCN分别代表两种基础的神经网络结构。LSTM是经典的循环网络结构，将数据按次序进行一轮迭代处理后输出特征；FCN则由卷积神经单元逐层组成，每层网络只提取特征的局部信息，多层网络叠加后才能得到最终特征。单独使用这两种网络分别可以达到91.12%和92.76%的诊断准确率。而biGRU+CNN和Multi-Conv+LSTM都组合使用了这两种基础网络结构，并且都在诊断准确率上有一定的提升。biGRU+CNN采用了双分支的并行结构，意味着两个分支都需要学习原始数据到高层特征的映射，并没有实现两种结构的互补。而MultiConv+LSTM单分支串联起两种网络，较浅的卷积单元设计用于平滑数据，提取邻域特征，而后续的LSTM从处理后的数据中提取高层特征。从结果上看，MultiConv+LSTM也取得了一定的优势。另外，加上度量学习损失函数后，诊断准确率进一步提升了1.26个百分点。

表4 各算法故障诊断准确率对比Table 4 Comparison on fault diagnosis accuracy of different algorithms

另外，使用精确率、召回率和F1得分三个指标评估MultiConv+LSTM模型的结果如表5所示。受各类样本数量不均衡的影响，模型对于正常运行类别的样本能够达到较高的精确率和召回率，而逆变器运行故障和逆变器短路故障这两类的召回率相对较低。但总体上，MultiConv+LSTM仍然达到了不错的效果。

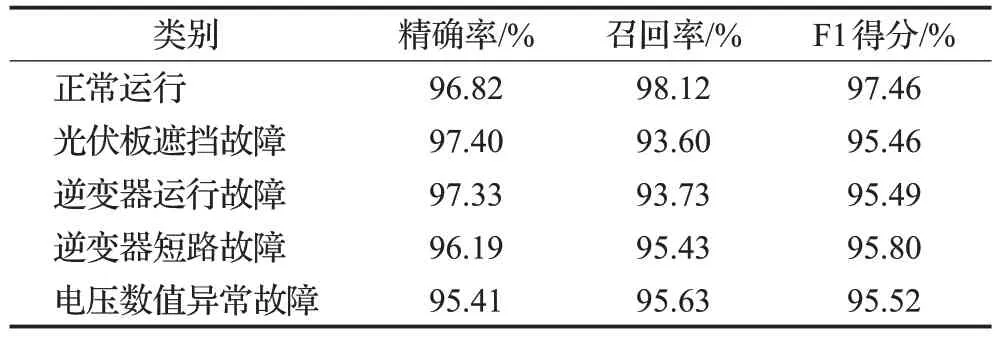
表5 MultiConv+LSTM的其他指标评估Table 5 Evaluations on other metrics of MultiConv+LSTM

3.3.3 多尺度特征提取对比实验

表6展示了组合不同尺度卷积单元时的故障诊断准确率。表中卷积单元数量为1时，网络结构就是没有使用多尺度特征提取机制的普通卷积单元。使用尺度为3的卷积时，诊断准确率为92.74%，而尺度为3、5的多尺度卷积使准确率提升至95.6%；尺度为5的普通卷积和尺度为5、7的多尺度卷积也有明显的准确率提升。从中可以看出，组合卷积单元进行多尺度特征提取能够有效提升模型的诊断准确率。另外，尺度为3的卷积核在本模型中起到了重要作用，只使用尺度为5、7的卷积核时，模型的表现甚至低于LSTM，说明大尺度卷积核确实存在信息丢失的问题，也证明了多尺度特征提取的必要性。

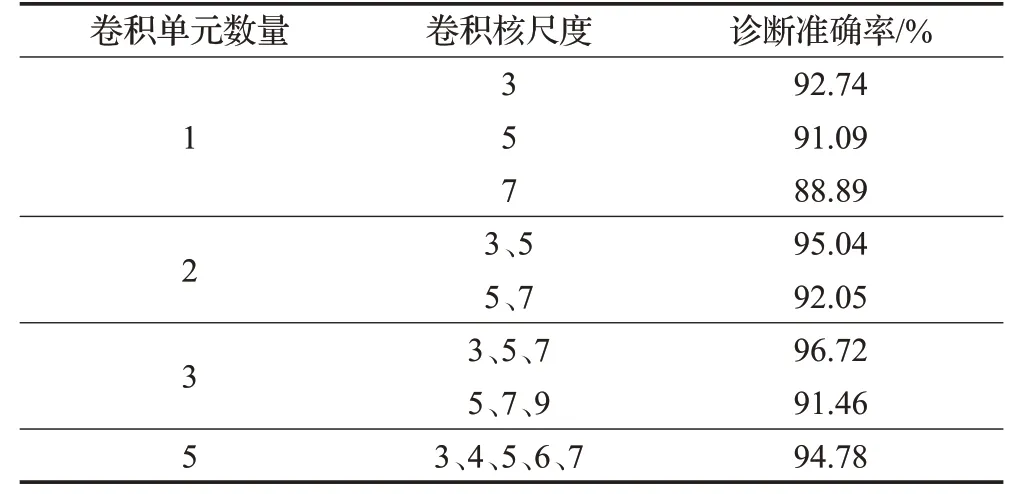
表6 不同尺度卷积组合的准确率对比Table 6 Comparison on accuracy of different scale combinations of convolutional units

从表6中可以看出，卷积单元数量为3，卷积尺度为3、5、7时，算法效果最佳。而将卷积单元数量增加到5时，诊断准确率有所下降，原因是5组卷积特征拼接得到的多尺度特征维数过高，给LSTM的训练增加了负担。

3.3.4 加权损失函数对模型训练的影响

本实验探究了加权交叉熵损失函数对诊断模型的作用。分别使用了加权交叉熵损失函数与常规交叉熵损失对模型进行了训练，实验结果如图7所示。因为训练数据中大部分为正常运行样本，少部分为故障样本，所以使用不带权重的交叉熵损失函数训练时，网络倾向于将样本预测为正常运行。这个问题不会体现在故障诊断准确率上，但对故障样本的召回率有很大影响。加权交叉熵损失函数为数量较少的样本加上较大的权重，从而产生较大的梯度，使得这些样本能够对参数的学习产生更大的影响。从图7可以看出，加权交叉熵损失函数能够有效提升故障类别的召回率。

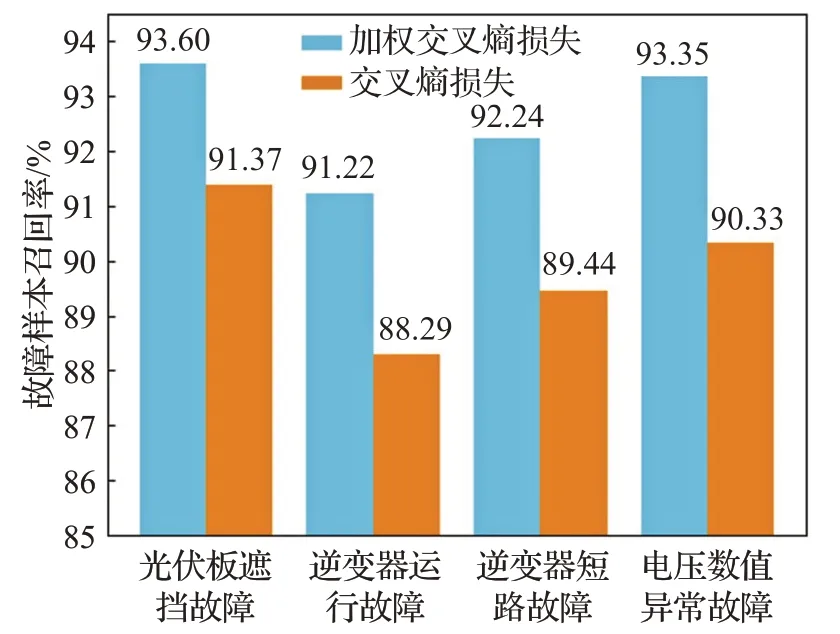
图7 加权交叉熵损失对故障诊断召回率的提升Fig.7 Recall of fault diagnosis w/o weighted cross entropy loss

4 总结

本文提出了一种基于多尺度时序特征的光伏系统故障诊断模型，实现了对正常运行设备、光伏板遮挡故障、逆变器运行故障、逆变器短路故障和电压数值异常故障这五种状态的精准诊断。本文设计了数据规范化算法，以矫正设备差异、天气差异给故障诊断带来的影响；设计了多尺度邻域特征提取模块，以解决光伏电站监测数据波动大、噪点多的问题。实验结果证明了本文提出的数据规范化算法的有效性，也表明了MultiConv+LSTM模型已经足够满足实际应用场景的要求。

基于本文的研究仍有一些方向值得探索。一方面，可以考虑细化故障的分类，实现更具体的故障诊断；另一方面，可以考虑在故障样本数量有限的情况下，进一步提升模型对故障样本的召回率。