COVID-19智能体模型及城市疫情封控措施评价研究
李江川,张健钦,杨 木,宫 鹏,邓少存,贾礼朋
1.北京建筑大学 测绘与城市空间信息学院,北京 102616 2.自然资源部城市空间信息重点实验室,北京 102616 3.清华大学 地球系统科学系,地球系统数值模拟教育部重点实验室,北京 100084
新冠肺炎(COVID-19)是由新型冠状病毒SARSCOV-2引起的一种呼吸道传染病,具有传播性强、潜伏期长等特点[1]。自2019年12月,新冠肺炎疫情在我国武汉市大规模爆发,而后席卷全球,造成巨大的人员伤亡与经济损失。随着国内疫情趋于稳定,各个城市开始恢复生产生活。但国外疫情形势仍然严峻,外来输入病例和进口冷冻生鲜可能会导致各地疫情出现小规模反弹。由于疫情反弹城市所采取的封控措施势必会对城市的平稳运行和市民生活带来影响,对疫情反弹后城市封控尺度进行科学分析可以为相关政策制定提供支持。
目前,对COVID-19疫情的增长预测与防疫政策评价分析多采用建模分析的手段[2],基于群体模型或个体模型进行研究。其中,群体模型基于SIR[3]、SEIR[4]、SEIAR[5]等动力学模型或结合长短记忆神经网络(long shortterm memory,LSTM)[6]、差分自回归移动平均模型(auto regression integreate moving average,ARIMA)[7-8]等统计学模型或机器学习模型对疫情进行增长预测与政策评价,如范如国等[9]构建了SEIR模型预测武汉COVID-19疫情拐点,徐韧哲等[10]构建了SIQR模型评价深圳市COVID-19疫情期间的防控政策。虽然群体模型能够在数值上做出准确预测,对于宏观尺度的政策评价较为准确,但模型调整上不够灵活,难以评价精细化的管控措施[11]。而个体模型是利用智能体(agent)模型或复杂网络模型对疫情扩散场景进行仿真,模拟疫情在对应场景下可能出现的趋势与结果,继而进行疫情预测与政策评价[12],如潘理虎等[13]采用基于智能体的仿真建模方法对太原市医院、政府应对COVID-19的政策措施进行了多情景仿真实验,叶锺楠[14]建立城市空间网络模型对COVID-19在武汉市内的传播情况进行模拟。个体模型在模型的调整上具有灵活性,模型的实现和结果可与地理信息系统(geographic information system,GIS)、数据可视化等技术结合,更加充分地挖掘各类信息间的关联关系,刻画疫情在空间上的传播过程以及对精细化、小尺度范围实施政策的评价。
鉴于上述背景,本文以某市为例,基于个体模型中的多智能体仿真和复杂网络模型,构建新冠肺炎疫情演变城市空间智能体仿真模型,模拟疫情在城市中的传播,并基于地图进行展示。由于多智能体模拟过程计算量大,其结果具有不确定性,且疫情传播过程存在马尔科夫特性[15](即疫情状态未来的状态,只与现在所处状态有关,而与以前的状态无关),本模型利用马尔科夫蒙特卡洛方法(Markov chain Monte Carlo,MCMC)[16-17]得到结果稳定分布后对模型中关键参数进行动态率定。本文利用该模型对疫情反弹后城市封控的尺度对疫情扩散的影响程度进行分析并提出建议,为可能到来的新一轮疫情反弹的防控措施制定提供参考。
1 研究区域与数据
本文选取具有典型城市特征的某大型城市作为研究区域。该市人口众多,人员复杂,交通发达,人群密集活动区域较多,极易受到传染病威胁且造成严重后果。以2020年新冠肺炎疫情为例,该市先后经历了早期湖北地区输入与本地扩散、春季境外输入与扩散、夏季某市场聚集疫情和秋冬季多点散发四个过程。
本文收集了以上部分过程的疫情数据。同时,由于空间智能体模型仿真过程中需要基础地理信息数据用于构建虚拟地理环境和生成智能体,且疫情传播与人员出行活动关系密切,本文收集了该市的基础地理信息数据与出行统计数据。相关数据说明如表1所示。
2 模型设计与实现
通过对已有数据的初步梳理,本文以城市中活动的居民为智能体,设计并实现智能体模型模拟在不同政策措施下病毒在城市人群流动与交互过程中的传播。模型根据已有的新闻报道、统计资料与论文研究,将智能体按照出行群体划分成不同的人群(学生、上班族、其他群体),按照土地类型对人群活动场所进行划分(住宅、学校、工作场所等),根据出行统计数据为智能体分配出行轨迹,构建虚拟地理环境模拟感染者在所在场所(家庭、医院、公共场所等)与其他智能体的交互、病毒的传播和感染者健康状态的转换,通过政策措施调整部分规则和智能体属性,并以疫情真实数据为参照率定模型中的关键参数。
2.1 模型总体框架
模型整体分为三层总体框架,如图1所示。
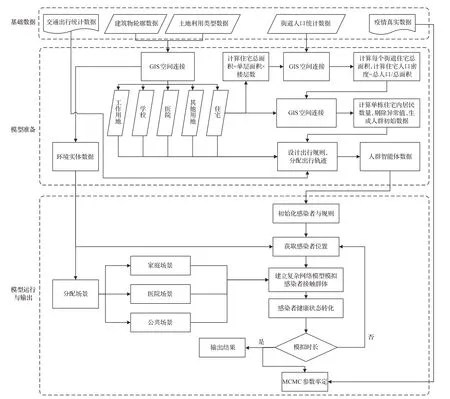
图1 模型总体框架Fig.1 Overall framework of model
第一层为基础数据层。该层主要提供模型所需的基础数据(表1)。
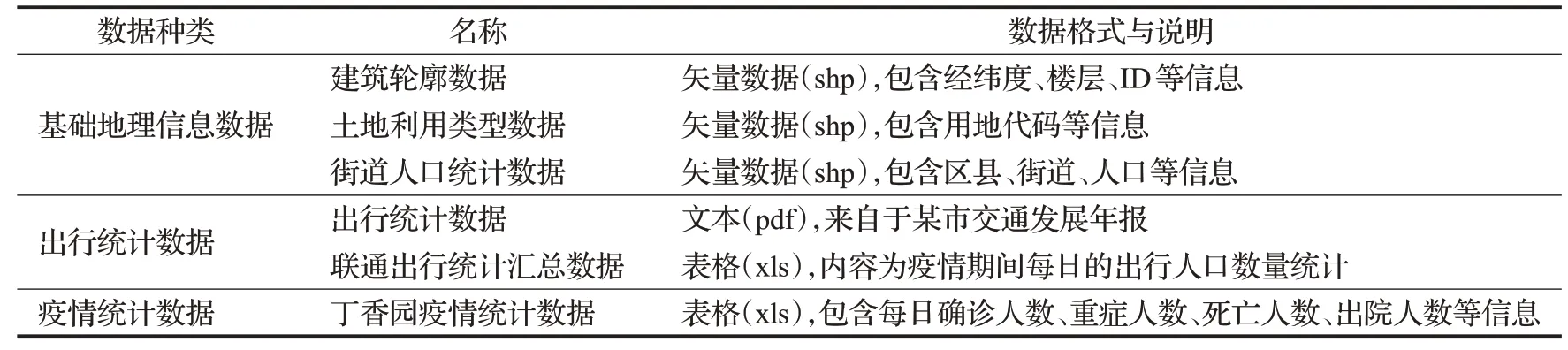
表1 研究数据Table 1 Research data
第二层为模型准备层。该层通过将数据层中矢量数据利用GIS进行空间连接操作,获取每一栋建筑用地类型,生成环境实体数据(属性如表2所示),提取并计算每个街道的住宅总面积和人口密度,将每个街道人口分配到每一栋住宅的各个楼层中,生成同等数量的人群智能体数据,每个智能体代表一名居民,设计智能体出行规则并为智能体数据分配出行轨迹记录。

表2 环境实体属性Table 2 Environmental entity attributes
第三层模型运行与输出层。该层通过上一层输入的智能体数据与环境实体数据,设定初始感染者、模拟时长、步长(本文设定8小时为一步长)和由于政策原因产生的特定规则与参数,模拟开始后进行感染者接触群体模拟与健康状态转化,到达模拟时长后输出模拟结果。模型通过MCMC方法确定参数,输出结果用于可视化展示和统计分析。
2.2 智能体属性与出行规则
根据《xx市交通发展年报》(以下简称年报)对城市居民出行目的统计分析结果,本文将人群智能体分为三类出行群体,分别为学生、上班族和其他群体,为其赋予属性,如表3。然后基于三类出行群体出行时间统计结果和模型设定的步长确定智能体的出行规则。规则如表4所示。
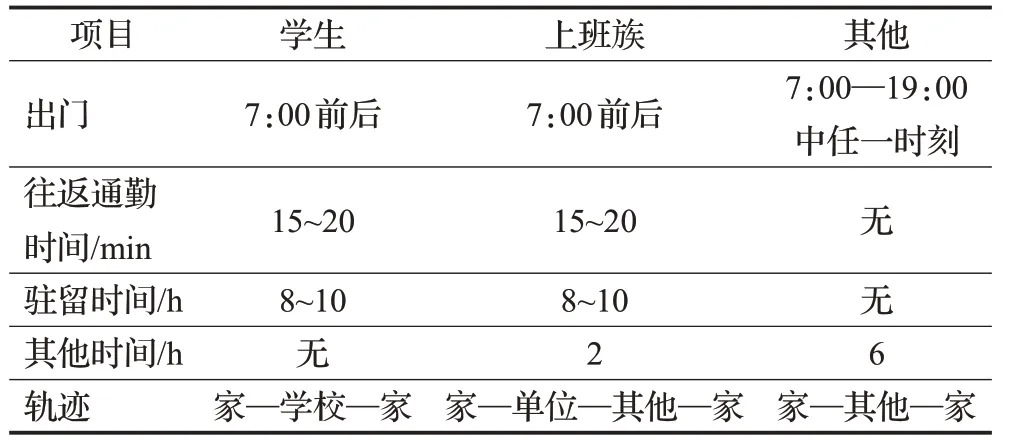
表4 智能体出行规则Table 4 Travel rules of agent
根据上述出行规则,本文根据就近原则,为agent数据分配不同时刻所处环境实体的编号,并保存至属性字段(表3)中。当模型开始运行后,模型通过不断改变模型的pos字段实现agent在虚拟地理环境中的移动。
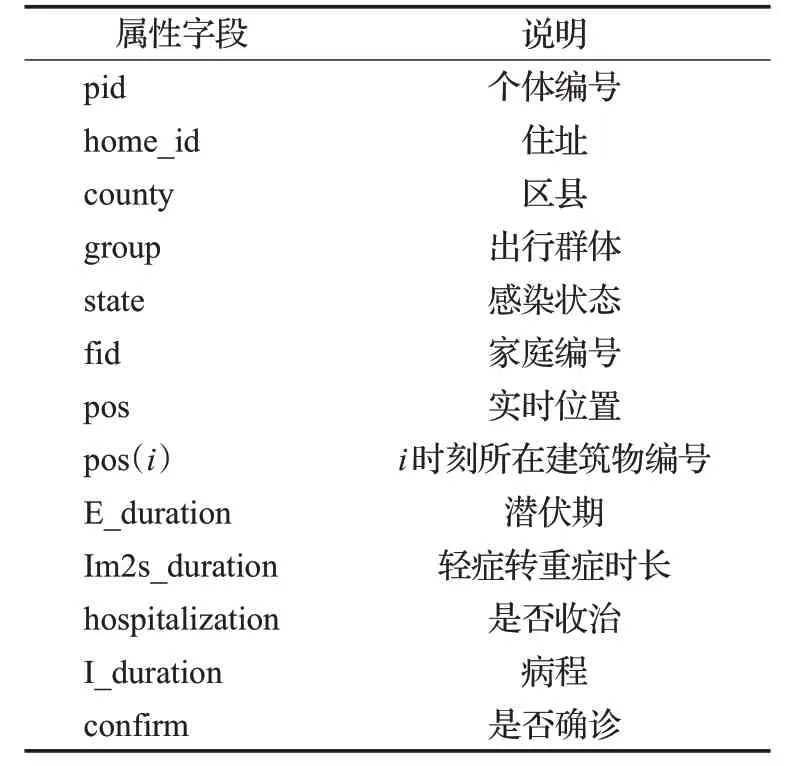
表3 智能体属性Table 3 Attributes of agent
此外,本文还需考虑相关政策对于智能体移动规则以及模型中部分参数(出行比例、感染概率、复工比例)的影响。本文根据2020年1月至3月的相关新闻资料整理和联通出行比例的统计结果,对模型相应时间段的管控措施做出如下设定,如表5所示。

表5 不同时间段管控措施Table 5 Control measures for different time periods
2.3 感染者接触群体模拟
新冠肺炎传播方式有直接传播(飞沫、呼吸等)、气溶胶传播、接触传播[1]。因此,对感染者所接触个体的关系网络进行模拟,能够刻画出病毒的传播路径。
复杂网络是一种可用于描述不同个体间交互关系的模型,它可分为随机网络、小世界网络、自相似网络、无标度网络等[18]。其中,小世界网络是由Watts和Strogatz根据人类社会中个体之间关系的特点提出。该网络中大部分节点互不连接,但可以通过其他节点抵达,它能够刻画人群中个体之间的交互关系[19]。故本文选取小世界网络模拟在不同建筑物内感染者的接触网络。
如图2所示,当易感者与未被收治的感染者处在同一栋建筑物时,根据不同建筑物的类型,以感染者为中心构建对应的小世界网络表示感染者及其接触者,设定接触后易感者感染的概率为pInfect,通过设定随机数与pInfect的比较确定接触者是否被感染,实现病毒向感染者的相邻节点传播。考虑到不同环境中感染者接触人数对病毒传播的影响,本文通过调整小世界网络中的参数(重连概率、相邻节点数)实现不同环境下智能体互相接触,利用蒙特卡洛方法对不同建筑物内人群接触和病毒传播的模拟结果取平均值与实际感染案例进行对比,率定家庭环境、医院环境、公共场所环境(含室外场所如公园、广场)小世界网络中重连概率为0.3、0.5、0.2,最大相邻节点数为7、8、4。
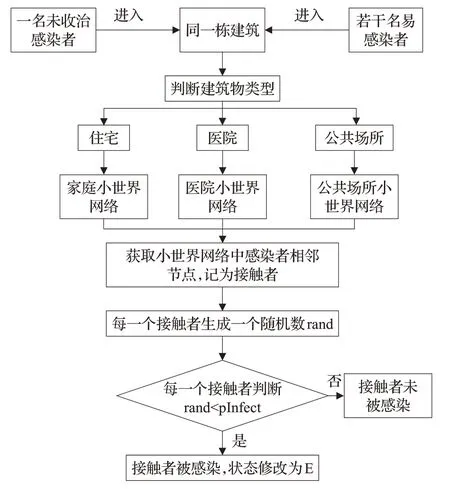
图2 感染者接触感染规则Fig.2 Contact infection rules for infected persons
2.4 感染者健康状态转换规则
在传染病模型中,人群一般可分为易感(S)、潜伏(E)、发病(I)、移除(康复(R)或死亡(D))四种状态[20]。此次依据新冠肺炎发病程度又可以将发病人群细分成轻症感染者(症状轻微,记为Im)、重症感染者(症状严重,记为Is)和无症状感染者(潜伏期过后携带病毒但仍未发病,记为In)[1],同时感染者的确诊和收治情况又对疫情的传播有着较大影响。因此本文引入上述状态与过程构建转换规则。规则如图3所示。
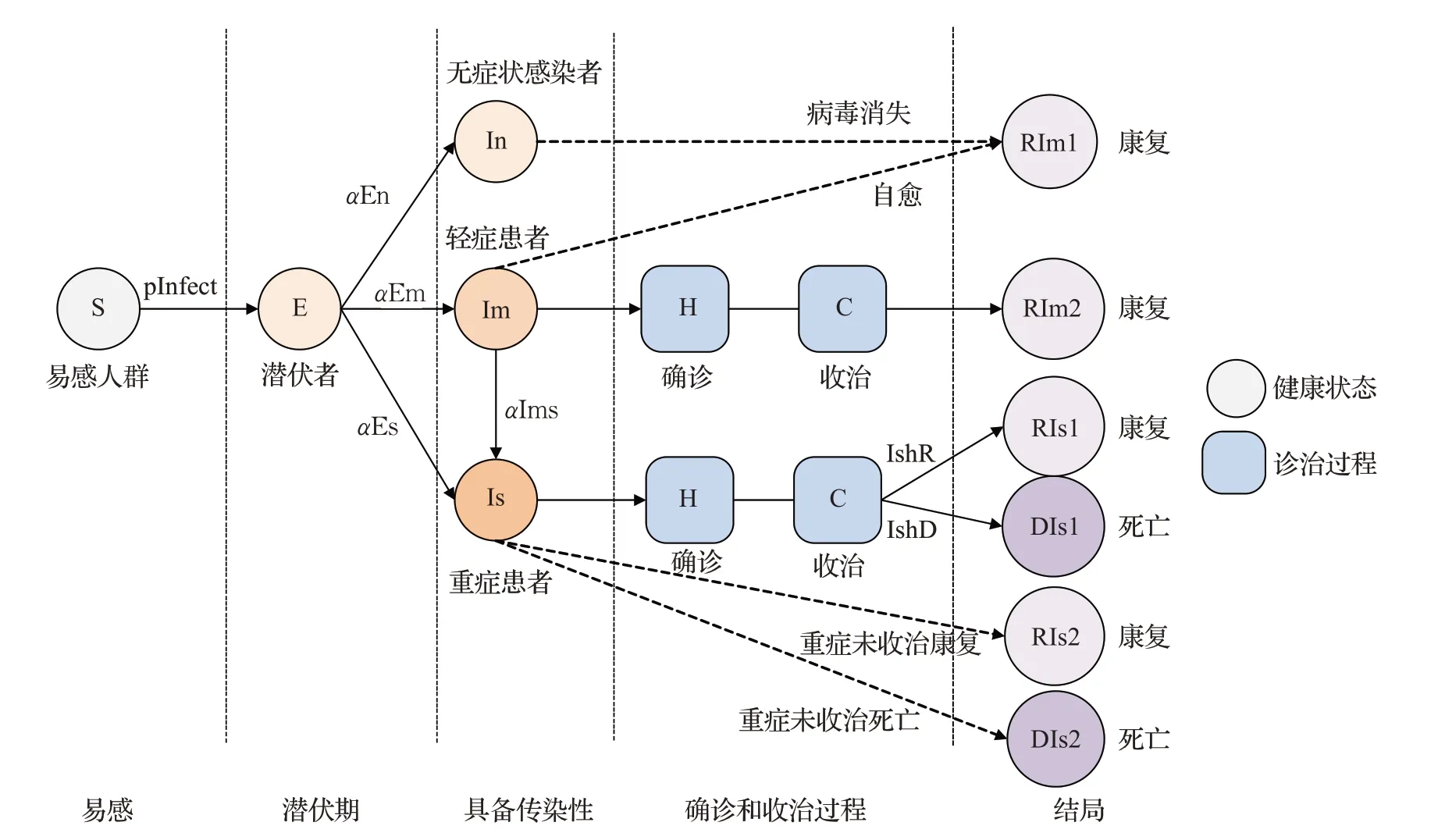
图3 健康状态转换规则(虚线表示未出现或忽略不计)Fig.3 Health status transition rules(dotted line means not present or ignored)
参考2020年3月至5月的新冠肺炎的流行病学调查与疫情统计数据[1],转换过程中相应参数取值如表6所示,其中无法查明的参数通过参数估计取值。
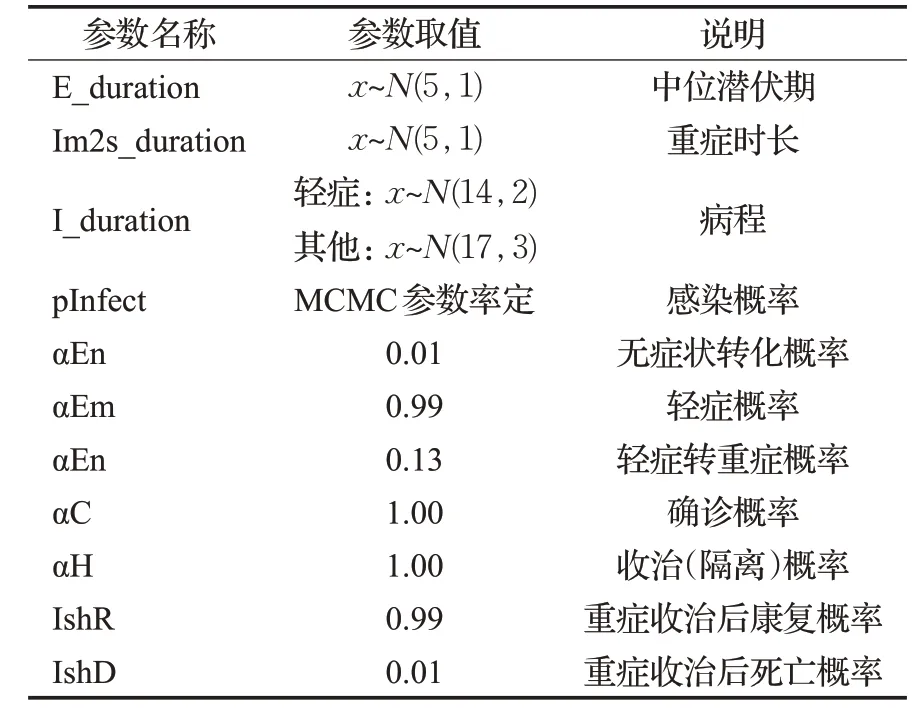
表6 参数设置Table 6 Parameter settings
2.5 模型实现与参数率定
模型实现以该市疫情早期增长(1月20日—3月8日)为例。根据该市卫健委公布的信息,模型设定两名位于D区的智能体作为初始感染者,模拟步长为8小时,模拟时长为50天。按照图1的流程运行后,发生感染事件的地点分布图如图4所示。
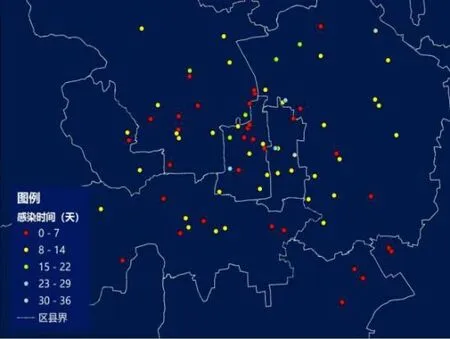
图4 模拟实验中感染事件分布示例Fig.4 Example of distribution of infection events in simulated experiment
模型数值结果以真实疫情的确诊人数为观测值,利用MCMC方法进行大规模采样与迭代得到模拟值的稳定分布,通过贝叶斯拟合探索合适参数取值范围。经过1 000次MCMC迭代[21],将采样结果与真实值建立线性回归方程,通过衡量方程中的系数来确定程序中未知参数pInfect:

式中,y为模型真实值,̂为模型拟合值。当输出结果α接近1,β接近0时,模型的模拟值最接近真值,模型参数为最优参数。
同时,为验证参数率定结果合理性,本文将MCMC采样、最小二乘法和人工粗调参三种方式的结果进行对比,利用拟合优度(R2)和方程(1)的系数进行比较,R2的计算公式如下:
式中,为观测值平均值。未知参数最佳估值如表7所示。
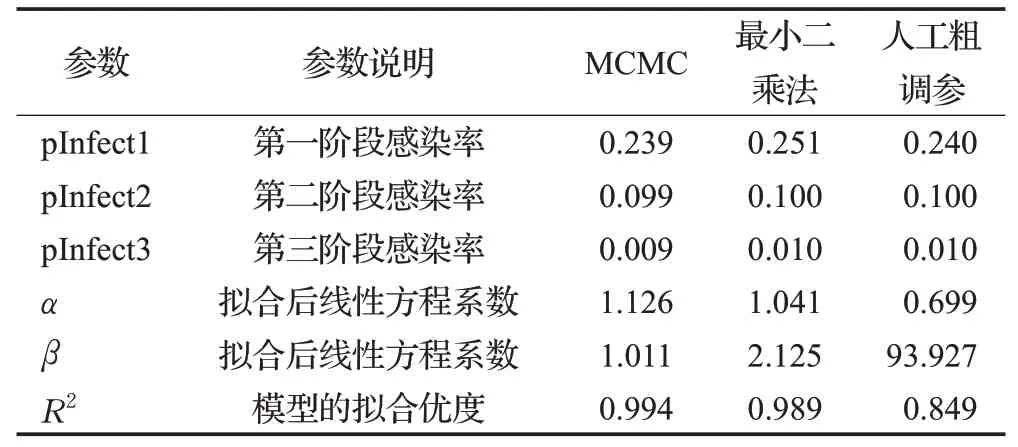
表7 参数率定结果对比Table 7 Comparison of parameter settings
从表7中可以看出,三个阶段的最佳感染率MCMC采样后拟合的取值分别为:第一阶段为0.239,第二阶段为0.099,第三阶段0.009。拟合后的系数α=1.126,β=1.011。由于MCMC采样结果较为稳定,相较于其他两种方式的拟合优度较高。对采样拟合后的结果取平均值,与真实值对比如图5所示。
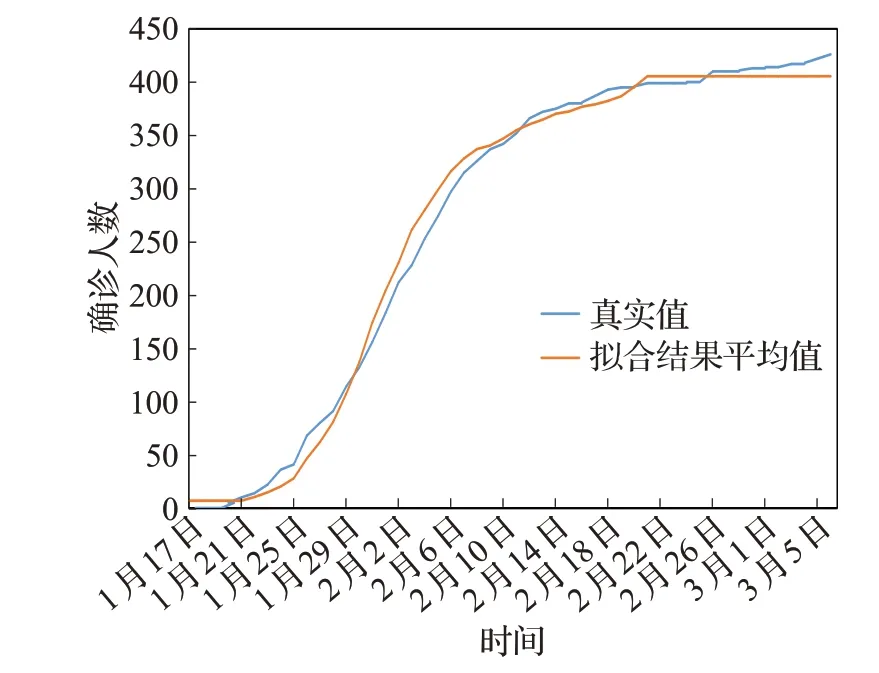
图5 拟合结果与真实值对比Fig.5 Comparison of fitting results with true values
如图5所示,采样结果的拟合值与真实值接近。说明模型在率定参数后,能够较为真实地反映早期疫情的演变情况。后续仿真实验中可以以上述参数为基准,根据不同的模拟步长和相关数据调整和推算模型对应参数,模拟不同的场景。
3 不同尺度封控的仿真实验分析
随着疫情防范进入常态化,一旦出现疫情反弹,如何进行封控才能使得对城市运行影响最小化的问题开始显现。因此,本文从封控的尺度展开研究,结合前文所述的城市空间智能体模型与根据真实场景率定的模型参数,通过模拟实验探究在相同初始感染人数和场景设定下不同封控尺度对感染人数增长与感染区域扩散上的影响。
3.1 实验场景设计
实验场景参考该市夏季聚集性疫情和其他地区多点散发场景进行设计。场景分为单点爆发与多点散发两种,详细设定如下:
(1)单点爆发疫情:假设该市B区某地(环境实体编号为171911)出现20名聚集性病例,初始状态设定为E。
(2)多点散发疫情:假设该市3个区出现20名散发病例,出现位置在区内不固定,初始状态为E。
所有模型参数中,感染概率(详见2.5节)的数值通过基准参数和对该市夏季聚集性疫情多次模拟后的结果进行对比,率定为0.025。实验分别从3个封控尺度进行仿真模拟,即无封控、社区封控、区县封控。三种尺度的场景说明如下:
(1)无封控:疫情开始后,政府未发布任何封控措施,仅对发病者及时收治。
(2)社区封控:疫情开始后,政府对出现发病者的建筑物以及患者的住址及其相邻的建筑物进行封控,封控地区所有人员一律居家不得外出,密切接触者全部被隔离。
(3)区县封控:疫情开始后,政府对出现发病者的区县展开封控,封控地区所有人员一律居家不得外出,密切接触者全部被隔离。
模型的模拟时长为20天,模拟的重复次数为25次。
3.2 实验结果分析
3.2.1 不同封控尺度对确诊人数增长的影响分析
针对25次模拟结果,本文分别统计了平均值、最大值和最小值。从表8显示的模拟输出的感染人数不同统计结果来看:在单点爆发出现的情况下,采取社区封控措施后确诊人数相较于无封控措施的感染人数下降了19%。对比社区封控和区县封控,社区封控的平均值和最大值略低于区县封控,两者最小值相等。在多点散发出现的情况下,采取区县封控措施的确诊人数较无封控下降了27%,采取社区封控措施较无封控措施下降了19%。说明在两种模式下社区封控对疫情增长抑制效果较为接近。同时,比较区县封控和社区封控,可以看到当多点散发出现时,社区封控和区县封控的确诊人数平均值和最小值相近,但社区封控的确诊人数最大值远高于区县封控,和无封控结果接近,说明在极端条件下,社区封控也可能存在确诊人数剧烈增长的风险。
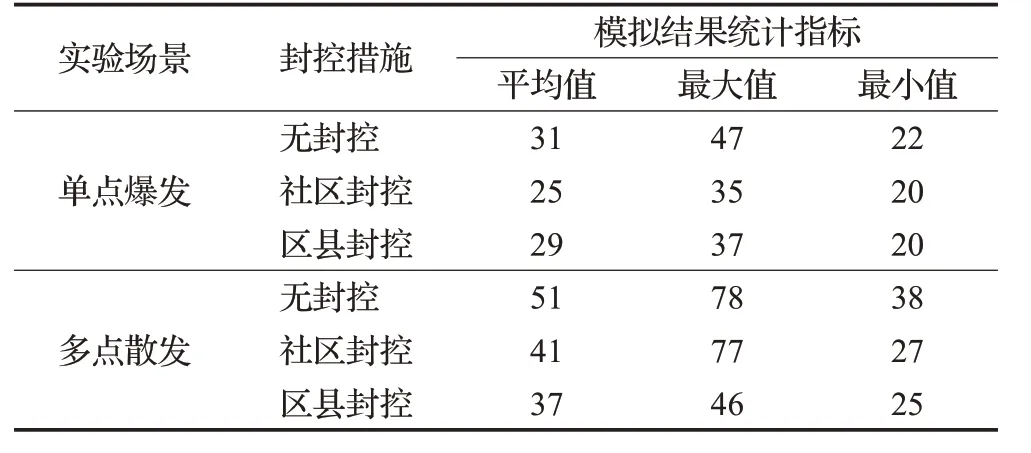
表8 不同尺度封控措施下模拟确诊人数对比Table 8 Comparison of number of simulated confirmed cases under different scale containment measures
对模拟结果取平均值绘制增长曲线,如图6所示。在相同初始感染者的情况下,多点散发的增长幅度高于单点爆发。两种疫情模式的主要增长时段在3~10天,之后由于感染者大部分被收治,增速放缓。此时单点模式下转为阶梯式增长,散发模式下除无封控措施外,其他实验组的增长速度逐渐放缓直至平稳。对比两种封控尺度,在单点爆发模式下,社区封控确诊人数早期高于区县封控,后期低于区县封控,而在多点散发模式下,区县封控早期确诊人数与社区封控无明显差异,中期明显高于社区封控,后期低于社区封控。
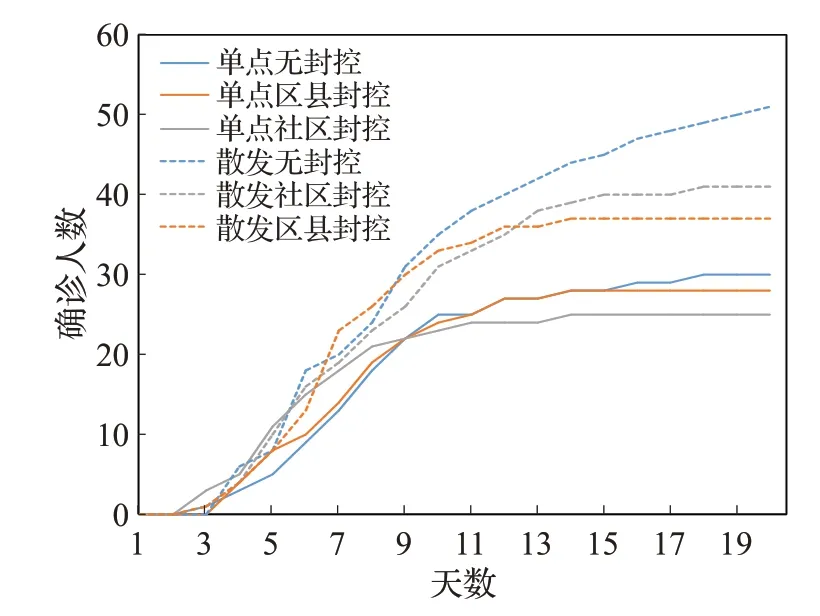
图6 三种措施下模拟确诊人数增长情况Fig.6 Growth situation of simulated confirmed cases under three measures
3.2.2 不同封控尺度对感染事件发生地数量的影响分析
本文收集了三种不同封控措施的模拟实验过程中发生感染事件的地点,以单点爆发模式为例,将其中部分实验结果展现在地图上,如图7所示。
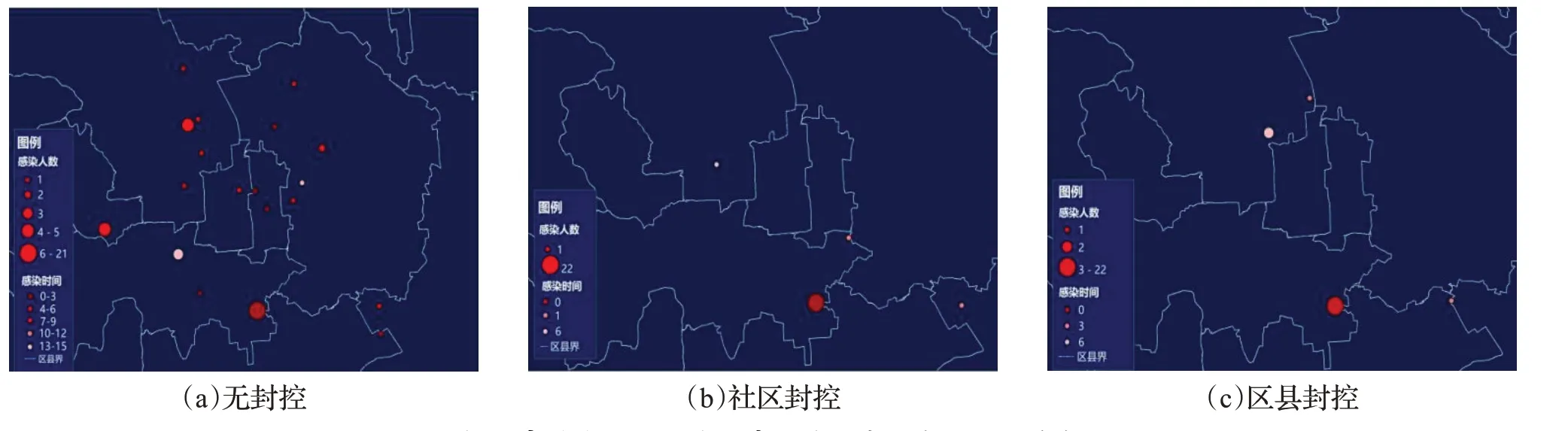
图7 实验中三种封控尺度下感染事件发生地点分布Fig.7 Distribution of infection incident locations under three containment scales in experiment
从图7可以看出,在单点模式下,若无封控措施情况,多区都出现了感染事件,除B区的爆发点外,其他区出现了多个小规模感染者聚集中心,感染事件发生地点数量超过了其他两种情况。社区封控和区县封控则将感染事件发生地点数量降低至4处,且感染事件地点在空间上较为分散。
考虑到实验过程中感染事件出现位置存在不确定性,影响实验结果,本文对所有实验中除疫情爆发点之外的所有发生感染事件地点数进行了汇总(取平均值),如表9所示。
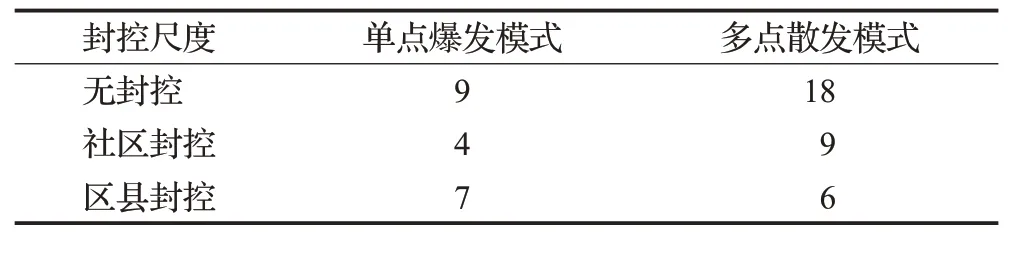
表9 感染事件发生地数量平均值对比Table 9 Comparison of average number of infection incident locations
从表9显示的结果来看,两种模式下,社区封控较无封控措施下感染事件地点数量下降了50%~55%,影响效果大致相同。而在区县封控下,单点爆发模式中感染事件地点数量下降了20%,多点散发模式中感染事件地点数量下降了66%。
同时,本文对六种情况下所有模拟实验中除疫情爆发地点外的感染事件发生地点数量的平均值的增长情况进行了对比分析。如图8所示,在20天的模拟时长中,感染地点数量增长前期呈近似直线增长,后期由于感染者大部分转入收治,传播过程被逐渐控制,因此大部分过程增速减缓,逐渐转为阶梯式增长,且阶梯长度逐渐增长,阶数逐渐减小,并在第9~11天逐渐趋于平稳。其中,单点社区封控在第3天转入阶梯增长,单点区县封控第4天转为阶梯增长,单点无封控和散发社区封控在第6天转入阶梯增长,散发区县封控在第7天直接转入平稳,而散发无封控在第12天转入阶梯增长。同时,单点爆发的感染事件发生地的增长和多点散发区县封控在前3天增速基本一致,多点散发模式下无封控和社区封控的增速前5天基本一致,因此出现小规模感染事件后的3~5天是封控的最佳时机。
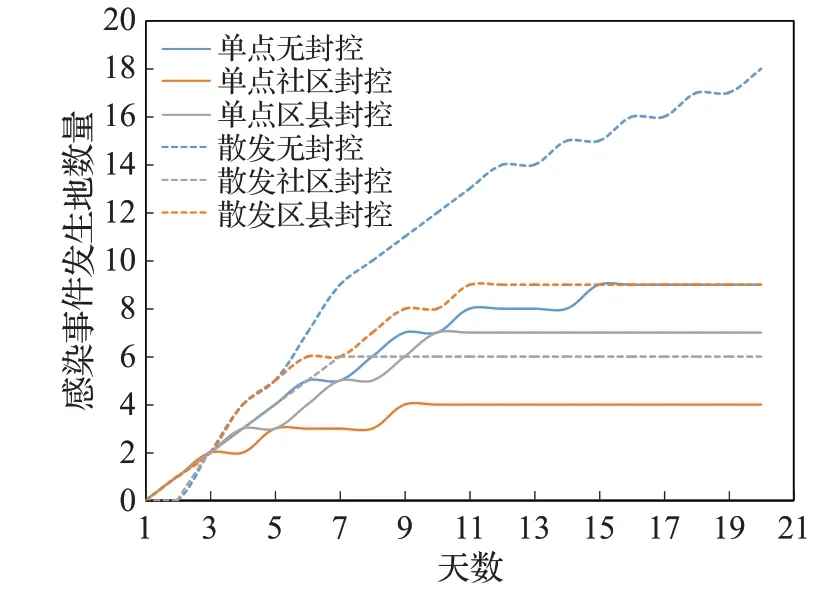
图8 三种措施下感染事件发生地增长情况Fig.8 Growth situation of infection incident locations under three measures
3.2.3 感染事件不确定性对实验结果的影响分析
由于模型为概率模型,每一次实验过程中被感染者传染的智能体编号具有不确定性,这一方面导致了感染地点的不确定性,另一方面导致了不同实验中确诊人数存在差异。因此本文对同一条件下多次模拟实验结果进行分析,并以单点无封控条件下模拟结果为例讨论这种不确定性对实验结果的影响。
对模型输出的确诊人数输入SPSS软件中绘制直方图(图9)和正态性检验(表10),可以看到模拟结果显著性P值均大于等于0.2,服从正态分布。实验结果95%置信区间为[28,33],平均值为31。

表10 正态性检验结果Table 10 Results of normality test
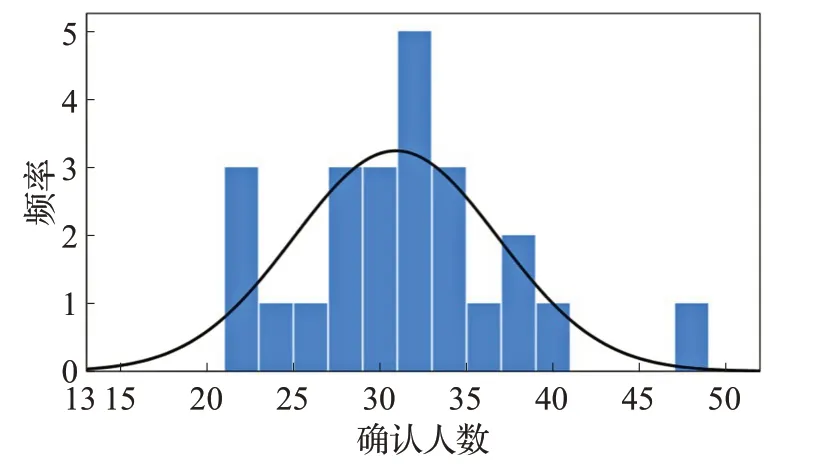
图9 模拟确诊人数分布直方图Fig.9 Histogram of distribution of simulated confirmed cases
鉴于上述分析,说明模型在率定参数后,感染过程的随机性会导致结果出现差异,这种结果跟所感染的智能体与其接触者有关。但模拟结果服从正态分布,因此在场景模拟时需要重复性模拟并确定结果置信区间以保证结果精确性。为探索合适的重复模拟次数,本文分别计算了实验中不同实验次数n下模拟结果y的平均值mn,并计算mn的总体标准差σ、样本标准差σn和95%置信区间范围c,以分析模拟结果平均值的敛散性,其中mn和σn的计算公式如下:
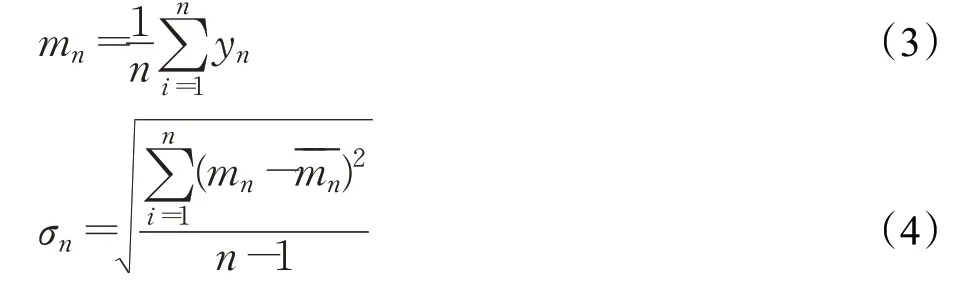
计算得出置信区间范围c后,根据总体标准差结果确定收敛区间范围为Δy=c+σ=0.64+1.56=2.20。对比模拟结果的样本标准差,平均值在第12次之后开始转为收敛,因此模拟次数可以设置在12次以上。
4 结束语
本文基于智能体建模与复杂网络模型,结合GIS技术构建了一个针对某市疫情的新冠肺炎疫情扩散模型。模型通过MCMC方法确定模型中关键参数。利用该模型,本文复现了该市2020年2月至3月疫情扩散情况,多次模拟的数值结果平均值与真实值较为吻合。
利用该模型,本文以单点爆发和多点散发两种模式为背景设计实验场景,探究不同尺度下的封控措施对感染者数值上增长与感染区域扩散的影响。研究发现:在不同尺度的封控措施中,社区封控的作用效果在两种疫情模式下基本接近,在单点爆发模式下遏制感染人数增长与空间扩散好于区县封控,在多点散发模式下劣于区县封控。同时,启动封控措施的最佳时机是出现病毒携带者后的前3~5天,但此时患者一般处于潜伏期或无症状状态不易被发现。结合相关传染病防治措施研究[22]与对国内一些聚集性疫情致因的研究[23],建议对高危地区定期组织筛查(如海鲜市场、海产品加工厂、冷库、渔港码头等地),要定期开展对人与物的核酸检测,及时筛查出无症状感染者与阳性环境标本。一旦发现核酸阳性标本后及时展开封控与消杀,防止疫情出现大规模扩散。实验结果中感染者数量增长主要在3~15天,建议出现少量感染者的地区在18~20天确认疫情增长情况稳定后可适当放宽封控措施。
模型考虑通过记录环境实体编号来描述智能体的运动,将计算与可视化分离,通过高性能计算资源参与计算,提升了模型的计算速度;同时模型的规则与参数调整更加灵活,适合模拟不同场景下疫情增长情况。但是智能体位置有空间随机性,因此模拟结果并不能在空间上如实反映疫情的真实扩散情况,同时模拟结果也具有一定程度的不确定性。因此在接下来的研究中,可以考虑更多的因素(例如短步长、室外短时活动人群交互、气象等)介入,提升运算的速度和模拟次数,使得模拟的结果更加稳定和精确,并设计更多的场景,为国内易接触病毒地区和国外疫情缓和后应对新一轮疫情反弹与其他传染病防治措施评价提供帮助。

