以降低洪水位为目标的河道疏浚规模与效果研究

郭庆超，陆 琴

（1.中国水利水电科学研究院 泥沙研究所，北京 100048；2.流域水循环模拟与调控国家重点实验室，北京 100038；3.水利部泥沙科学与北方河流治理重点实验室，北京 100048）

1 研究背景

疏浚作为一种清淤工程措施在河道治理、航道和港池维护、水库库容恢复、灌区引水渠运行、河湖污染物移除等方面得到广泛使用［1-6］。然而由于疏浚后往往会发生回淤，疏浚效果不能长期保持，需要重复进行疏浚才能使疏浚效果得以维持，清淤成本较高。因此对于许多疏浚工程而言，疏浚后的回淤问题是最受关注的。为此，不少研究者开展了疏浚回淤问题的研究，涉及到河道、湖泊、河口和海洋等场景，采用的方法包括现场监测、资料分析、模型试验、数学模型计算和经验公式等。方春明等采用数学模型，对河道挖槽疏浚后回淤过程的一般规律进行了模拟研究［7］，刘文博等对洞庭湖环保疏浚后的回淤速率进行了研究［8］，袁胜英等根据实测资料对伶仃洋河口湾航道试挖槽泥沙回淤问题进行了分析［9］，曹慧江等利用二维潮流及泥沙数学模型和回淤公式对港珠澳大桥岛隧工程沉管基槽开挖回淤强度进行过分析和估算［10］，GUO、王蒙等采用数学模型对河床局部挖坑的冲淤及再平衡过程进行了模拟［11-12］，刘家驹、罗肇森等通过建立基于一定物理机理的经验公式计算港池和引航道回淤［13-14］。这些研究为疏浚后的回淤强度评估和运行维护发挥了重要作用。

然而由于担心疏浚后发生回淤，疏浚效果不能长期保持，在冲积性河流进行以降低洪水位为目标的河道疏浚的案例很少，对于冲积性河流疏浚规模和效果论证的研究更少。事实上，对于某些河道，采用疏浚来降低洪水位，提高防洪能力是完全可能的。比如，对于冲刷型河道，由于其水流输沙能力大于含沙量，虽然疏浚后水流输沙能力有所降低，但只要保持疏浚后输沙能力不小于含沙量，疏浚后是不会发生回淤的，疏浚效果是可以长期保留的。对于微冲微淤型河道或者输沙总量较小或者低含沙量河流，只要疏浚以后水流输沙能力不明显小于含沙量，河道疏浚后即使有回淤，但是回淤总量很有限，疏浚效果仍然可以在较长时期内得以保持。目前，很多河流的流域水土流失治理效果显著，进入河道泥沙量大幅减少，再加上水利工程的拦沙作用，进入下游河道的沙量已明显小于河道冲淤平衡的临界值。比如近20年长江下游和黄河下游河道来沙量比2000年以前大幅度减少2/3 以上［15］，并可能在未来很长时期内维持很低水平［16-17］，河道发生了持续性冲刷。而松花江、淮河、珠江等河流本来总沙量就很少［15］，含沙量很低，再加上流域水土保持治理和水库拦沙的作用，使得这些河流的来沙更少，河道长期处于冲刷状态。对于这样的河道进行疏浚，以增加行洪能力，降低洪水位，不仅是可能的，而且因为不会发生严重回淤，效果可以长期保留［18］。

由此可见，在流域来沙大幅减少、河道普遍出现由淤积向冲刷转换的大背景下，利用河道疏浚来降低洪水位是可行的，河道疏浚必然成为未来河道防洪治理的一个新措施。然而，在实际运用中，至少需要回答以下三个科学技术难题：（1）如何确定疏浚对降低洪水位或增加过流能力的效果？（2）如何确定合理疏浚规模？（3）如何长期保留疏浚效果？对这三个问题的回答，即构成本文的主要研究内容。

2 河道水力因子关系推导

这里所说的水力因子主要包括流量、流速、比降、过流面积、水面宽（河宽）、平均水深等。对于宽浅的冲积性河流，其水力半径R可近似等于平均水深h，水流平均流速可以用曼宁公式表示如下：

式中：V为断面平均流速；C为谢才系数；n为曼宁糙率；J为水面比降。考虑到河相系数ζ=B1/2/h（B为水面宽），则由式（1）得：

而在天然河流中，根据实测水文资料，可以点绘上下游相邻两个水文站的水位流量关系，从而可以得到某一流量Q下的河段水面比降，进而点绘比降与流量关系，可以得到如下关系式：

式中k1和α1分别是系数和指数。

同样，根据水文站实测的水力要素和断面资料，可以计算不同水深的河相系数ζ，再点绘河相系数与水深关系，可以得到：

式中k2和α2分别是系数和指数。

将式（3）和（4）代入式（2）得到如下关系式：

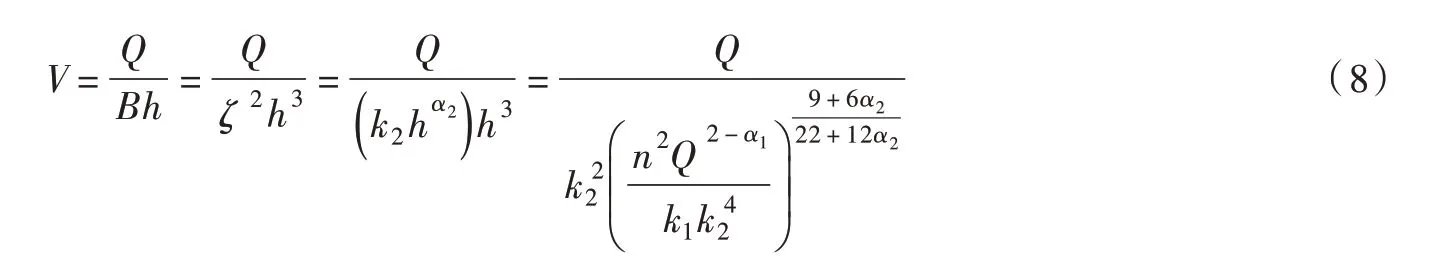
式（5）—式（8）给出了主要水力因子与流量或水深之间的关系，均成单因素关系，即只需要已知流量或水深，就可以求解其他所有主要水力因子，大大方便了应用，提高了解决实际问题的能力和效率。

3 疏浚对降低洪水位效果计算方法

疏浚对河道的防洪作用可以通过两个参数分别评价，一个是同流量水位的下降值ΔH，另外一个是平滩水位时行洪能力的增加值ΔQ，如何计算这两个变量，是本节需要解决的问题。

假定对某河道进行疏浚以降低洪水位，断面的疏浚面积为ΔA，疏浚深度为ΔZ，河道疏浚长度为L，其疏浚对降低水位的效果如示意图1 所示。需要说明的是，疏浚前后下端点的水位流量关系保持不变，上端点的ΔH为疏浚后同流量的水位下降值，上端点至下端点之间河段沿程水位的下降值可通过水面线计算或简单按照沿程线性插值确定。

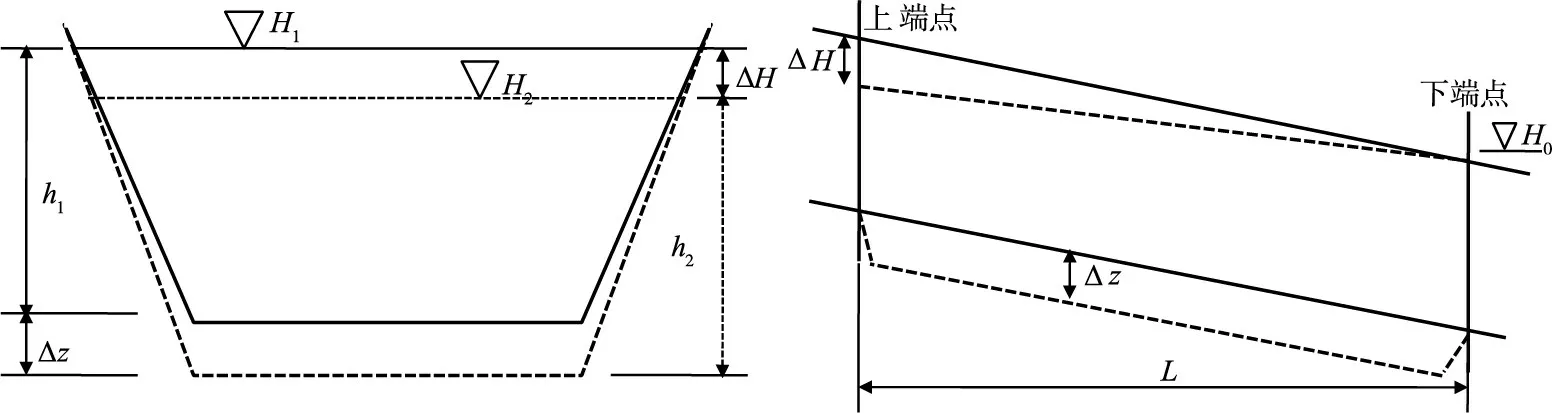
图1 河道疏浚及水位变化示意图

对于疏浚前，当洪水流量为Q时，由曼宁公式得：

式中：变量名下标“1”表示疏浚前；H0和H1分别为疏浚前流量为Q时疏浚河段上端点和下端点的水位；q为单宽流量，可表示为：

由于河道疏浚对河宽影响很小，因此可近似认为疏浚前后单宽流量是相同的。由式（9）得疏浚前流量为Q的上端点水位为：

式中h1为疏浚前上端点断面的平均水深，可由式（6）计算确定。同理，疏浚后洪水流量为Q时上端点水位H2的计算式与式（11）类似，即：

式中变量名下标“2”表示疏浚后，h2为疏浚后上端点断面的平均水深，可近似表示为：

用式（11）减去式（12）并利用式（13），即可得到疏浚后流量为Q时疏浚河段上端点洪水位的下降值ΔH：

当给定断面疏浚深度ΔZ和河道疏浚长度L，即可由式（14）结合式（6）和式（10）计算洪水流量为Q时，疏浚后洪水位的下降值ΔH。

疏浚后河道的最大过流能力的增加值ΔQ可以用疏浚后满槽时的平滩流量Qbf2与疏浚前的平滩流量Qbf1之差表示：

式中：Qbf1可由水文站实测资料确定；A1和Jbf1分别为疏浚前的平滩面积和满槽时的水面比降，可由式（3）（6）—（7）计算确定；ΔA为断面疏浚面积。

至此，在断面疏浚深度为ΔZ或疏浚面积为ΔA、河道疏浚长度为L时，推导了疏浚河段上端点的洪水位下降值和过流能力增加值的计算公式，可以直接用于疏浚对提高河道防洪能力的论证评估。

4 疏浚规模确定方法

这里所说的疏浚规模包括两方面的含义，一是断面疏浚面积或深度，其量值大小是由疏浚后回淤程度所决定的，确定原则是疏浚后水流输沙能力不小于含沙量，即以不发生回淤作为控制条件；二是河道疏浚长度，其量值大小是由降低洪水位程度所决定的。从防洪角度来看，疏浚规模越大越好。但是，由于疏浚后水流输沙能力会下降，如果断面扩大太多，势必会发生回淤，致使疏浚效果难以长期保留。这里以冲刷型河道为例，来阐述合理的断面疏浚规模的确定方法。

对于冲刷型河道，即水流输沙能力大于含沙量，比如松花江的哈尔滨江段、淮河蚌埠以下河段等，对这些河段实施一定规模疏浚来降低洪水位是可行的，只要满足疏浚后的水流输沙能力不小于含沙量S*≥S即可。这里，以疏浚后水流输沙能力恰好等于含沙量S*=S，即疏浚后恰好保持河床冲淤平衡，此时对应的断面疏浚面积或疏浚深度即为河道断面的疏浚规模，超过此规模，疏浚后必然回淤。至于河道的疏浚长度，由式（14）可知，疏浚河段越长洪水位下降越多，但是疏浚成本也越大，因此合理的河道疏浚长度是由希望达到的防洪标准（即疏浚河段上端点的洪水位下降值）所决定的。

河道疏浚后的水流挟沙能力公式为：

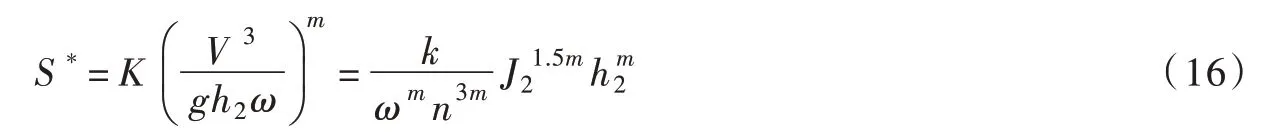
式中：k和m为挟沙能力系数和指数，可按照文献［19-20］来确定；ω为泥沙沉速，可由实测资料确定；h2为疏浚后流量为Q的断面平均水深，可由式（13）确定；J2是疏浚后流量为Q时的水面比降，可由下式计算：

对于少沙河流或者微冲微淤河道，也可以通过河道疏浚来降低洪水位，虽然疏浚后会发生回淤，但是完全可以把回淤总量控制在一定规模内。如此，疏浚效果也可以在一个较长的时期内得以保留，此时的合理疏浚规模可以按照疏浚后水流挟沙能力不小于0.8 倍的含沙量作为约束条件来确定，即S*≥0.8S。

5 应用范例

为了阐述该方法在实际中如何应用，本文以松花江哈尔滨江段和淮河蚌埠以下河段为参考对象，构建一个应用范例，详细说明合理疏浚规模的确定以及疏浚后洪水位下降值、过流能力增加值的计算过程。

5.1 数据准备在正式计算之前，需要根据相邻两个水文站的实测水文泥沙和断面资料，逐一确定基本参数的具体数值，这些参数包括河道糙率n、泥沙沉速ω、挟沙能力系数和指数，疏浚前的平滩流量Qbf1、比降与流量关系式中的系数和指数、河相系数与水深关系式中的系数和指数等。表1给出了某河段的上述基本参数的具体取值。表中Jbf1、Bbf1、hbf1和Vbf1分别由式（3）和（6）—（8）计算而得，A1=Bbf1hbf1。

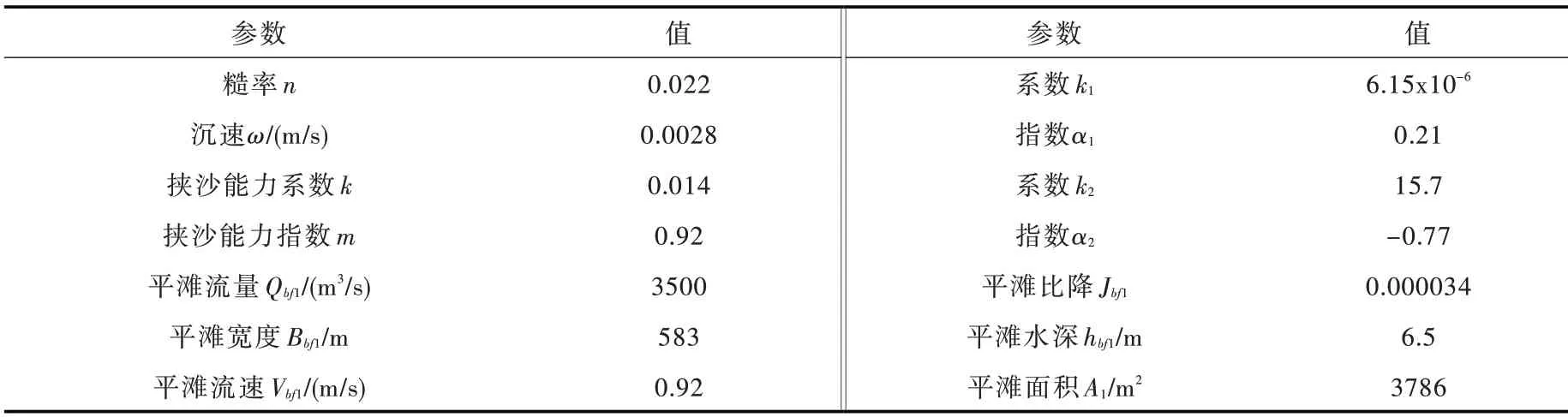
表1 河道疏浚前基本参数及其取值

5.2 防洪效果计算由式（14）知，只要给定疏浚河段长度L，断面疏浚深度ΔZ（或疏浚ΔA），就可以计算某一流量下疏浚后的水位下降值ΔH。下面以疏浚前的平滩流量Qbf1为例，说明不同疏浚深度ΔZ和长度L条件下，上端点水位下降值ΔH的计算步骤。

（1）假定断面疏浚深度ΔZ和河道疏浚长度L为某数值；

（2）根据式（6）（7）（10），计算出h1、B1和q；

（3）根据式（14）试算得到疏浚后水位下降值ΔH；

（4）改变疏浚长度L，重复步骤（2）和（3），得到不同疏浚长度的上端点水位下降值；

（5）改变疏浚深度ΔZ，重复步骤（2）—（4），得到不同疏浚深度的上端点水位下降值。

表2和图2 给出了以疏浚前平滩流量3500 m3/s 为例，不同疏浚深度和长度条件下，上端点水位下降值的计算成果。疏浚后平滩流量可由式（15）计算，结果也列于表2中，通过与疏浚前的平滩流量比较，可以评估疏浚对增加河道行洪能力的作用。从计算结果可以看出：

图2 不同规模疏浚后的洪水位下降值

表2 不同疏浚长度和深度的某流量下的上端点洪水位下降值（单位：m）

（1）在疏浚深度相同时，疏浚河段越长，洪水位下降越多，但是随着疏浚长度的增加，水位下降速率有减缓趋势。短距离疏浚对降低洪水位效果微弱，只有长距离疏浚才能明显降低水位，比如对于断面疏浚深度1.0 m 的情况，疏浚2 km 长的河道只能降低水位2.5 cm，但是如果疏浚长度为50 km，则可以降低水位42.2 cm。由此可见，要想通过河道疏浚来降低洪水位，必须采用长距离疏浚。

（2）在疏浚长度相同的情况下，断面疏浚越深，洪水位下降越明显，但是随着疏浚深度的增加，水位下降速率也有减缓趋势。

（3）断面疏浚越深，过流能力增加越大。以河道疏浚长度50 km 为例，按三种疏浚深度1.0 m、1.5 m 和2.0 m 疏浚后，河道平滩流量分别是4359 m3/s、4816 m3/s 和5291 m3/s，行洪能力比疏浚前的平滩流量3500 m3/s 分别增加24.5%、37.6%和51.2%。

5.3 合理疏浚规模计算合理的断面疏浚规模是根据疏浚后基本不回淤，即水流挟沙能力与含沙量基本相等的原则来确定的，而合理的河道疏浚长度是由上端点同流量水位下降值确定的。在本计算案例中，以河道疏浚长度50 km 为例，通过计算疏浚后的挟沙能力，并与实测的含沙量进行比较，给出合理的断面疏浚规模。

表3和图3 给出了利用式（16）计算的三种断面疏浚规模下不同流量的挟沙能力，以及与疏浚前的含沙量比较。从计算结果来看，对于断面疏浚深度1.0 m 和1.5 m，对应的疏浚面积分别是500 m2和750 m2的情况，疏浚后的挟沙能力仍然大于同流量的含沙量，说明这样规模的疏浚不会发生回淤。而当断面疏浚深度为2.0m 或疏浚面积达到1000 m2时，当流量小于3900 m3/s 时，疏浚后的挟沙能力已经小于含沙量，这时会发生一定的回淤；但当流量大于3900 m3/s 后，疏浚后的挟沙能力又大于含沙量，这时不仅不会发生回淤，反而可以把较小流量时的回淤泥沙冲走，从而可以基本保持疏浚后的冲淤平衡。因此，断面疏浚深度2.0 m 或疏浚面积1000 m2可以作为本案例的断面极限疏浚规模，此值可以作为河道疏浚设计的重要控制参数，也是河道疏浚效果能否长期保留的重要理论依据。当然，在河道实际疏浚工作中，疏浚规模可以小于此值，以保持不回淤；也可以略大于此值，此时虽然疏浚后有回淤，但是回淤强度很小，疏浚效果仍然能在较长时期内得以保留。

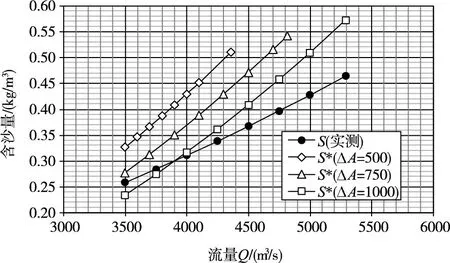
图3 不同规模疏浚后的水流挟沙能力与含沙量比较

表3 不同规模疏浚后水流挟沙能力计算结果

6 结论与建议

（1）根据河流动力学和泥沙运动力学的基本原理，并利用实测资料建立的比降与流量关系、河相系数与平均水深关系，推导了主要水力因子与流量或水深的单因素关系计算公式，只需已知流量或水深，就可以求解其他所有主要水力因子，大大方便了应用，提高了解决实际问题的能力和效率。

（2）推导了洪水位下降值与河道疏浚长度和断面疏浚规模之间关系的计算公式，给出了疏浚后河道行洪能力增加值的计算公式，为论证疏浚对提高河道防洪能力提供了理论依据。以疏浚后不发生回淤、疏浚效果可以长期保留为原则，将疏浚后挟沙能力不小于水流含沙量作为约束条件，建立了确定合理河道疏浚规模的技术方法。

（3）计算案例表明，疏浚河段越长，洪水位下降越多，但是随着疏浚长度的增加，水位下降速率有减缓趋势；短距离河道疏浚对降低洪水位效果不明显，只有长距离疏浚才能明显降低洪水位。

（4）本文建立的方法主要用于河道疏浚规模的确定和疏浚效果的评估，适用于长系列的平均水沙条件。但是对于某一年或短期水沙条件，疏浚河道会不会发生回淤？还需要借助水沙运动数学模型进行预测计算，以反映动床对疏浚效果的短期波动影响。