重力坝加高的应力和稳定计算方法及控制标准研究

张国新，钮新强，雒翔宇，颜天佑

（1.流域水循环模拟与调控国家重点实验室 中国水利水电科学研究院，北京 100038；2.长江勘测规划设计研究有限责任公司，湖北 武汉 430010）

1 研究背景

大坝加高是已建水库扩容增效的主要手段［1-3］，许多国家将大坝加高作为一种经济实用的水利工程再开发方式。文献［2］统计了截止2006年国外已建在建10 m 以上大坝加高工程91 座，涉及到22 个国家，其中加高工程较多的是美国、日本和西班牙，代表性工程有美国的罗斯福（Rooseuelt Dam）大坝（83.5 m/23.5 m：原坝高/加高），委内瑞拉的古里（Guri Dam）大坝（110 m/52 m），日本的黑部（Kurobe Dam）重力拱坝（120 m/68 m）。美国2013年完成的圣文森特大坝（San Vicent Dam）加高工程，将原高67 m 的重力坝加高36 m 至103 m，是美国加高幅度最大，且用RCC 施工的重力坝加高工程［4］。我国大坝加高始自1950年代［3，5］，以土石坝为主，文献［5］介绍的33 座大坝加高工程中22 座为土石坝，11 座为浆砌石坝或混凝土重力坝，其中丹江口大坝加高（97.0 m/14.6 m）是我国乃至世界上规模最大的大坝加高工程［1，6］。位于杭州的里畈重力坝加高一期将坝高从50 m 加高至72 m，计划进一步加高35 m 至107 m，目前正在进行大坝加高设计。

“后帮式”是重力坝加高的主要形式［4-8］，即在坝顶加高的同时，在老坝体的下游浇筑贴坡混凝土，加大坝体的断面厚度，提高大坝抗滑稳定性，以抵抗新增水压力。由于这种加高方式可不用放空水库，较大规模的重力坝加高大多采用这种方式，如委内瑞拉的古里、美国的圣文森特、我国丹江口均采用了这种加高方式。

后帮式加高重力坝的应力计算传统上采用材料力学法。日本的垣谷正道［7］推导了完整的计算公式，该方法在日本沿用至今。该算法假定：①新贴坡混凝土与老坝体完全结合；②新老混凝土的材料特性（弹性模量）相同；③新混凝土的自生体积变形忽略不计；④老坝自重和加高施工过程中的水沙压力由老坝独自承担，新坝块自重和加高后水沙压力的增量由新老混凝土块共同承担；⑤加高后的整体坝满足平截面假定；⑥不计温度荷载。在如上假定条件之下，按照平衡条件可以得到新老坝体的坝基应力分布，控制标准为基本荷载组合条件下：①坝踵不出现拉应力；②坝基混凝土压应力安全系数4.0；③加高后大坝的整体抗滑稳定安全系数按刚体极限平衡、摩尔-库伦准则计算，正常荷载组合下抗剪断稳定安全系数不小于4.0。

材料力学法同样是美国重力坝设计规范中的主要方法之一［4，9-10］，美国规范中称为重力法（Gravity Method），加高前的老坝和加高后的整坝应力进行分步计算，假定各截面的正应力分布为梯形、剪应力分布为抛物线形，利用上下游表面的边界条件和平衡方程求解各截面的应力分布。应力控制标准为基本荷载组合条件下：①坝基合力作用点位于中间1/3（坝踵无拉应力）；②最大压应力小于混凝土抗压强度的1/4，且不超过3.5 MPa；③整体抗滑稳定安全系数4.0。

我国重力坝加高设计目前没有独立的规范，仍采用常规的混凝土重力坝设计规范。设计阶段的应力和稳定分析虽然将有限元法作为重要手段之一，但体型设计时仍以材料力学法为主，应力和稳定的控制标准与新建重力坝相同，即基本荷载组合条件下：①坝踵无拉应力；②坝体压应力安全系数不小于4.0；③坝基压应力小于岩石抗压承载力；④沿建基面抗剪断稳定安全系数不小于3.0。

但是，“后帮式”重力坝加高有两个关键难题［1，7，11-16］：（1）新老坝块分载计算的问题。加高过程中老坝仍然处于挡水工作状态，且坝体随加高挡水断面不断变化，同时库水荷载和温度场动态变化，上述变化均对坝体应力计算方法提出了更高的要求；（2）新老混凝土结合的界面问题。在运行多年的老坝体加高培厚混凝土后，存在一个粘结强度较低的新老混凝土结合面，同时受到新老混凝土材料特性的差异、新混凝土水化热温升带来的温差及周期性变化气温等因素的影响，新老坝块结合面很容易脱开。丹江口大坝在加高设计阶段针对新老混凝土结合问题，自1994年11月—1999年3月在右5、右6 坝段先后进行了3 次现场原型试验研究，结果表明在经过一个完整的冬夏交替后结合面大部分脱开，且结合面随季节变化呈现出周期性开闭现象，即坝段两侧冬季张开、夏季闭合，中间区域夏季张开、冬季闭合的周期性变化。大坝加高施工过程中采取了一系列提高结合面强度的措施，结合面状况大为改善，但观测结果表明，结合面仍存在部分脱开现象。为解决如上难题，文献［1，6］提出了“后帮有限结合”加高结构设计新理论。

新老混凝土结合状态是影响加高后坝体受力和稳定性的关键因素之一，当结合面局部脱开后会改变新老坝体的分载状态［13］，进而影响到新老坝块的应力分布及稳定性，甚至会影响到大坝整体安全。根据分析可知，分载的比例取决于结合面的脱开比例及脱开部位。同时，新浇混凝土的水化热引起的新老混凝土温差也会影响结合面的开合状态、应力分布及稳定性［12］。但是新老坝体的脱开特性及新浇混凝土的温度变化均是材料力学法进行分析时无法考虑的。

有限单元法是复杂结构、复杂条件下应力计算、稳定分析及安全评估的优良方法，但是其计算结果具有网格敏感性，尤其是坝踵坝址等应力集中的部位，因此针对有限元结果往往难以给出统一的应力控制标准。美国将有限元法作为大坝加高细化设计与深化研究的基本方法［9-10］，为了避免坝踵等部位的应力集中，采用非线性有限元方法计算，成果应用时不分析坝踵拉应力，并且最大压应力控制标准与材料力学法相同。日本加高重力坝设计中有限单元法作为辅助方法用于校核设计方案，文献［7］以一个加高前后坝高分别为50 和65 m、下游坝坡0.85 的概化模型，研究了基础弹性模量、新老混凝土弹性模量、加高限制水位、新老结合面状况等对大坝整体应力和稳定的影响。可以看出，美国和日本在加高重力坝设计中均没有将新老混凝土结合面部分脱开作为一种设计状态来规定设计方法和标准，只是适当增大了坝体厚度。

有限元和材料力学法相结合的等效应力法，既可以考虑坝体的复杂结构又可以消除坝踵应力集中［17-18］，已是拱坝设计的规定方法［19］。对于常规重力坝，满足平截面假定的应力状态能够用平衡方程唯一求解［20］，但加高重力坝由于存在新老坝块分载和结合面局部脱开的情况，加高后的坝体不再是一个静定结构，坝基整体平截面假定将带来较大误差。基于上述问题本文提出新老混凝土有限结合的重力坝加高应力和稳定计算的等效内力法，以丹江口大坝加高工程为例，探讨不同工况条件下的应力和稳定控制标准。

2 加高重力坝的有限元分析

2.1 荷载分析后帮式重力坝加高前后受力状态如图1 所示，老坝坝高H1、底宽B1，加高后总坝高H2、总底宽B、新坝块底宽B2。图中①—⑥号荷载在加高前由老坝单独承担，①—④为加高限制水位及淤沙带来的水平荷载和竖向荷载，⑤为老坝自重，⑥为相应的扬压力荷载；⑦—⑪号为加高及抬高水位带来的水压、自重及温度荷载增量，由新、老坝块（即加高后的整坝）共同承担。新浇混凝土水化热导致的新老坝块温差⑪作为一个特殊工况计入永久荷载。

图1 新老坝受力示意

对图1 所示的加高重力坝进行有限元分析时，可以分简化计算和仿真计算两种。简化计算的步骤为：（1）老坝体及自重；（2）施加①—⑥号荷载；（3）新坝块及自重；（4）施加⑦—⑩荷载；（5）温差荷载。仿真计算则需要模拟新浇混凝土的分仓浇筑、浇筑过程中水位和温度的变化、水化热温升引起各项荷载的变化。

2.2 新老混凝土结合面的模拟后帮式重力坝加高后在老坝顶和下游面存在新老混凝土结合面，由于结合面两侧的混凝土存在材料特性差和温度差，使结合面上存在界面应力。同时结合面的强度一般小于混凝土本体强度，使得新老混凝土结合面容易张开成为一个实际存在的缝。实际工程中为了提高结合面的传剪能力，一般会设置键槽（见图2）。结合面的模拟有两种方式，即无厚度接缝单元和等效键槽单元。

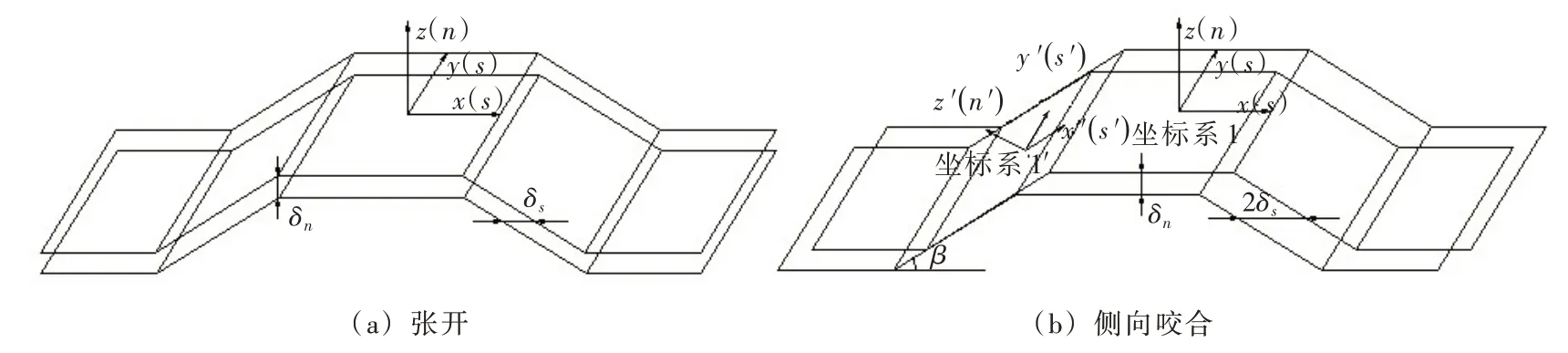
图2 键槽示意

2.2.1 无厚度接缝单元 对新老混凝土结合面的键槽进行精细网格剖分，图2（a）所示的键槽分成5个接缝单元。给定单元法向黏结强度和切向抗剪强度，当单元的法向应力大于其法向抗拉强度或剪应力大于抗剪强度时，接缝单元破坏，成为一条实际的缝。实际缝用接触单元模拟，接触单元可以传压，压紧之后可以传剪，但不能传拉。

计算中接缝单元有4种状态：粘结、接触锁定、接触滑移、张开。4种状态的弹性矩阵［D］定义如下：

式中Ks和Kn分别为缝单元的剪切刚度和法向刚度。张开时［D］的元素都为0。

2.2.2 等效键槽单元 当采用精细单元模拟键槽时需要大量单元和节点，影响计算效率，可以用等效概化的方式模拟，在本构关系上考虑键槽的影响。设缝的累积法向开度为δn，切向位移为δs，则缝的状态有如下3 种：

（a）δn≤0，闭合：αn=1，αs=1；

（b）δn＞0， |δs|＜δncotβ，张开：αn=0，αs=0；

（c）δn＞0，|δs| ≥δncotβ，张开：键槽侧面接触，αn =0，αs =1。

αn、αs为法向和切向接触刚度系数。当键槽侧面接触时需要考虑侧翼作用进行修正，即将局部坐标系下侧翼接触作用的法向刚度K n′和切向刚度K s′，转化成整体坐标系下法向刚度Kn和切向刚度Ks，且切向刚度又分为x和y两个方向，根据几何关系，有下式：

则法向和切向刚度修正系数：

式中ξ为键槽单边侧翼占单个键槽的面积比。对于弹性矩阵的修正如下：

2.3 有限元非线性分析的屈服准则非线性有限元法是分析大坝安全性态与极限承载能力的重要手段［21-23］，该方法已被纳入到《重力坝设计规范》（NB/T 35026-2014）中［20］，规定“在建基面屈服区全部贯通时，要求强度储备系数大于2.2”，但规范中未规定屈服准则，也未规定此K＞2.2所对应的作用（荷载）组合。

沿建基面的抗剪断抗滑稳定分析按下式［19］：

式中：f′、C′为坝基接触面抗剪断摩擦系数和黏聚力；∑W、∑P分别为滑动面的法向分力和切向分力之和；A为滑动面截面积。

在理想弹塑性有限元分析时，上式等价于给定滑动面的摩尔-库仑准则：

式中：τ、σn分别为沿滑动面的剪应力和法向应力；ϕ′、c′为沿滑动面的摩擦角和黏聚力。

数值计算和理论分析均可以证明，当按平面问题采用式（6）的屈服准则通过降强法进行有限元非线性计算时得到的抗滑稳定安全系数与式（5）的刚体极限平衡法一致。

有限元非线性分析一般按三维问题计算，三维应力状态下的摩尔-库仑准则为：

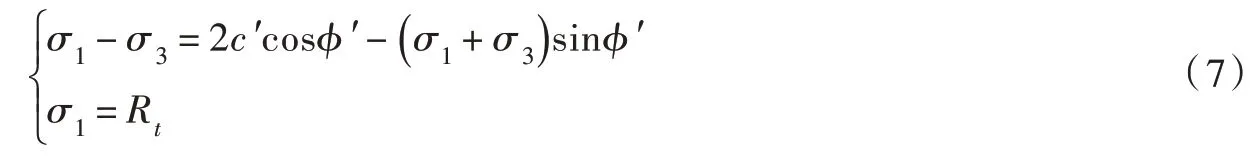
式中：σ1、σ3分别为第1、3 主应力；Rt为抗拉强度。

由于重力坝分坝段挡水，坝轴向自由，第一、三主应力往往出现在断面平面外，即最大剪应力τ不出现在断面平面内，且大于断面内剪应力，因此基于式（7）通过降强法进行非线性分析得到的安全系数往往小于刚体极限平衡结果。为便于与刚体极限平衡法结果比较，建议降强法计算抗滑稳定安全系数时：①给定滑动面；②取代表断面按平面问题计算；③屈服准则采用式（6）。

3 等效内力法

3.1 内力求解由于线弹性有限元应力结果具有网格依赖性，且在坝踵有应力集中现象，难以制定与有限元相适应的应力控制标准，可采用等效应力法解决上述问题。

等效应力法是基于有限元结果采用内力等效的方法求出沿指定断面（如建基面）的内力（见图3），进一步采用材料力学法求出应力，采用摩尔-库仑准则求抗滑稳定安全系数的方法。该方法可以发挥有限元和材料力学法两者的优势。等效内力的计算有两种方法，即应力积分法和直接内力法。

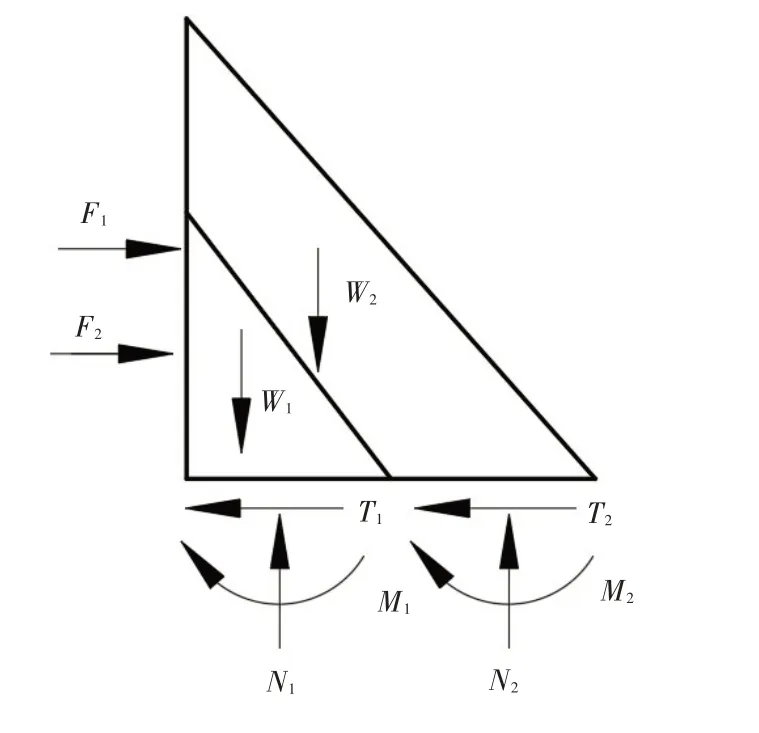
图3 新老坝块分载内力

应力积分法首先根据有限元结果求出建基面的法向和切向应力，再沿建基面进行积分求出内力。由于应力的精度比位移低一阶，应力积分法有时会有较大误差，本文采用文献［24］提出的直接反力法。

将老坝块、新坝块及基础看作3 个子域（图4），给定编号为1、2、3。设子域的子刚度为Kij、位移ui、外荷载为Pi；i，j=1，2，3；Fij为i、j子域之间相互作用力，则有限元方程为［24］：

图4 直接反力法的子域及相互作用力

求解方程（8）得到{ui}后，可用下式求出各子域之间的相互作用节点力：

式中：{F12}=-{F21}为新老坝块之间的相互作用力；{F31}、{F32}为基础对老坝块、新坝块的作用力。

新老坝块底部的局部内力按下式计算：

式中：{F31} |n，{F31} |T分别为{F31} 在老坝块底面法向和切向的分量；x为力的作用点。

3.2 新老坝块等效应力及局部安全系数已知新老坝块底部的局部内力后，可用内力求出建基面的等效应力：

式中σu、σm1、σm2、σd为加高后坝踵、老坝块坝址、新坝块上游、新坝块坝址的应力。

新老坝块的局部抗滑稳定安全系数为：

式中K1、K2分别为老、新坝块抗滑稳定安全系数。

4 算例

4.1 丹江口大坝加高典型坝段简介丹江口水库是南水北调中线的水源地，大坝加高是南水北调中线的龙头工程。初期工程竣工于1974年，坝顶高程162.0 m，正常蓄水位157.0 m，淤沙位115.0 m。大坝加高工程开工于2005年，2013年完工，坝顶高程提高至176.6 m，加高施工中限制水位145.0 m，加高后正常蓄水位抬升至170.0 m，设计洪水位172.2 m。丹江口大坝混凝土坝段分为右联坝段、右非坝段、深孔坝段、溢流坝段、厂房坝段、左联坝段，其中深孔、溢流、厂房各坝段的底宽在一期工程即按加高后建设，右联、右非、左联各坝段为完整的“后帮式”加高，7#坝段为最高的典型加高坝段，体型如图5。以7#坝段为代表，取新老混凝土结合面不同的状态，计算分析基本工况（正常蓄水位）条件下坝体应力和稳定的影响。主要计算参数如表1。有限元计算采用SapTis 程序［25］。

图5 丹江口重力坝典型坝段（单位：m）

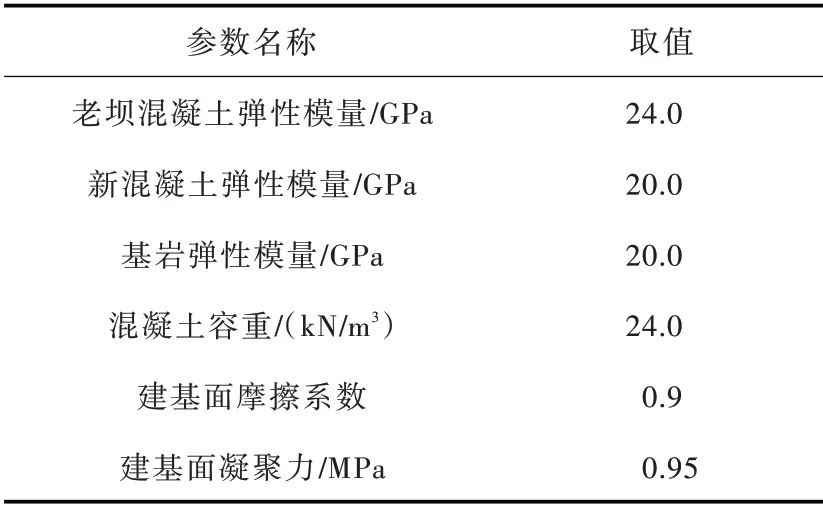
表1 丹江口大坝加高计算主要参数

4.2 结合面状态对坝基应力的影响将结合面顶部水平段、竖直段、倾斜段分为①—④段（如图6），模拟结合面不同部位不同的结合状态，其中水平段为粘结、接触两个状态，其余段为粘结、张开两个状态，取各段不同的状态组合，计算正常蓄水位170 m 时坝体应力和稳定，计算工况见表2，7 个工况中不计入新老混凝土温差作用。

图6 新老混凝土结合面分段

表2 结合面状态影响分析工况

各工况代表点的等效应力计算结果见表3，表中的应力拉为“-”。由表可见；（1）结合面状态对坝踵应力影响不明显，各工况坝踵均为压应力，最大压应力为0.9 MPa，最小0.58 MPa；（2）结合面上部（顶部、竖直段）的结合状态对坝基应力影响较小，顶部水平段由粘结变为接触、竖直段由粘结变为脱开，建基面各代表点应力变化小于5%；（3）贴坡段，尤其是贴坡下部的结合状态对建基面应力影响大，贴坡段全部脱开时可使建基面新建坝块的上游应力由0.7 增大至4.19 MPa，新坝块下游的竖向应力由压应力变为拉应力；（4）最大压应力出现在新老混凝土结合部位，老坝块下游最大值为1.35 MPa，新坝块上游最大值为4.19 MPa；（5）只要斜坡段最下部不脱开，全建基面即不会出现拉应力。

表3 各工况坝基代表点应力（应力拉为“-”）（单位：MPa）

图7为结合面全部粘结状态下（工况1）三种不同计算方法的建基面应力分布，即有限元法、有限元等效应力法（式（11））和基于加高后整坝平截面假定的材料力学法。可以看出，有限元法应力和等效应力法应力接近，而基于全坝平截面假定的材料力学法应力与有限元结果差距较大，表明“后帮式”加高重力坝的“加高后平截面”假定，与实际情况有较大出入。

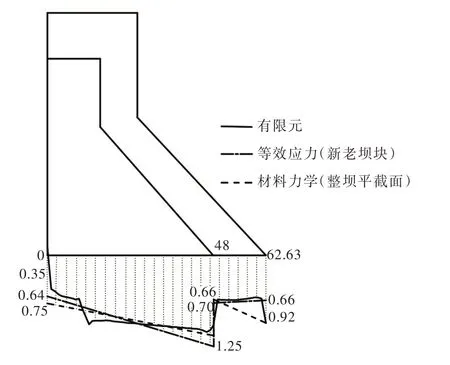
图7 不同方法建基面应力分布的比较（单位：MPa）

由表3所示的计算结果可见，新贴坡混凝土的强度等级为C20 以上，即可得保证建基面压应力安全系数4.0 以上。

4.3 整体和局部（新老坝块）抗滑稳定安全系数用式（5）和式（12）分别计算各工况的加高后大坝整体安全系数K及新老坝块局部安全系数K1、K2，计算结果如表4所示。算例中正常蓄水位条件下整体安全系数为4.37，且整体安全系数只与总竖向力和总推力有关，与结合面状态无关。新老坝块局部稳定安全系数与结合面状态相关，老坝块的最小值为竖直段和贴坡段均脱开的工况为3.74，其余工况均大于4.0。新坝块安全系数小于老坝块，最大值出现在贴坡段脱开工况，最小值出现在仅有贴坡下段粘结工况，最小值3.39。

表4 各工况整体和新老坝体局部抗滑稳定安全系数

基于计算结果发现，假定新老坝块结合完整，按整体平截面假定材料力学法计算新老坝块局部内力后的抗滑稳定结果，老坝块安全系数小于新坝块，规律与有限元等效内力法相反。分析有限元结果表明，自重荷载会产生上游坝体指向上游，下游坝体指向下游的剪应力，抵消了老坝体的水推力剪力，加大了新坝块的下游剪力，使老坝块安全系数增大，新坝块安全系数减小。

4.4 结合面粘结面积对局部抗滑稳定的影响计算分析表明，结合面粘结的部位直接影响到新老坝块的分载比例，相同粘结比例条件下粘结部位越靠近建基面，老坝块的安全系数越大，新坝块的安全系数越小。由表4可以看出新老坝块局部安全系数最小出现在贴坡段下段粘结，上部张开的工况，此时贴坡段下部粘结长度为24.3 m，占结合面总长度（含水平段）的27.2%，新坝块底部的抗滑稳定安全系数为3.39（170.0 m 水位），不断减小结合面长度，计算得到新坝块稳定安全系数如表5所示。根据计算结果，当贴坡段下部粘结比例达到17.5%，同时顶部结合面处于接触压紧状态时，最小局部抗滑稳定安全系数满足3.0 的规范要求，这个结果与文献［1，6］的“后帮有限结合理论”中的“结合面20%以上粘结即可保证大坝安全”的结论一致。建成运行8年以来，丹江口大坝已经受正常蓄水位的考验，实测最小结合度大于42%，表明大坝是安全的。

计算中未计入温度荷载，当计入新老坝块的水化热温差后，新坝块降温，会减小建基面法向应力，将进一步降低局部安全系数。

4.5 弹塑性有限元强度折减法为了便于和刚体极限平衡法及有限元等效内力法结果比较，此处的弹塑性有限元法取沿建基面的摩尔-库仑准则作为屈服准则（式（6））。

强度折减按下式进行：

式中：C n′、f n′为第n步计算折减后的抗剪参数；K n′为第n次强度折减系数，位移-折减系数曲线上的拐点对应的折减系数即为安全系数（见图8）。

由表2、表4、表5可以看出，新坝体最小安全系数出现在贴坡段下部粘结的工况，粘结面积占结合面积的17.5%以上时安全系数满足3.0 要求。以此为条件采用弹塑性力学法按式（13）进行强度折减，可得到老坝顶位移与强度折减倍数的关系，如图8 所示。从图中可以看出，折减系数小于3 时变形基本呈线性状态，当折减系数增大至3 时变形斜率发生变化，说明屈服区贯穿新坝块是在K=2.8 ～3.0 之间。随着强度折减倍数的加大，在K=4.2 ～4.5 时变形曲线发生第二次转折，变形急剧增大直至失稳，此处所对应的即是屈服区贯穿全坝。由计算结果还可以看出，水位170.0 m未进行强度折减时坝踵部位即出现由于应力集中而屈服的现象，当强度折减倍数达到3.25 时屈服区贯穿防渗帷幕。对比有限元强度折减的计算结果和表4、表5可以看出，弹塑性有限元法得到的新老坝块及整体安全系数与等效内力刚体极限平衡法一致。说明只要用相同的计算假定和屈服准则，刚体极限平衡法和非线性有限元法的抗滑稳定分析结果是一致的。

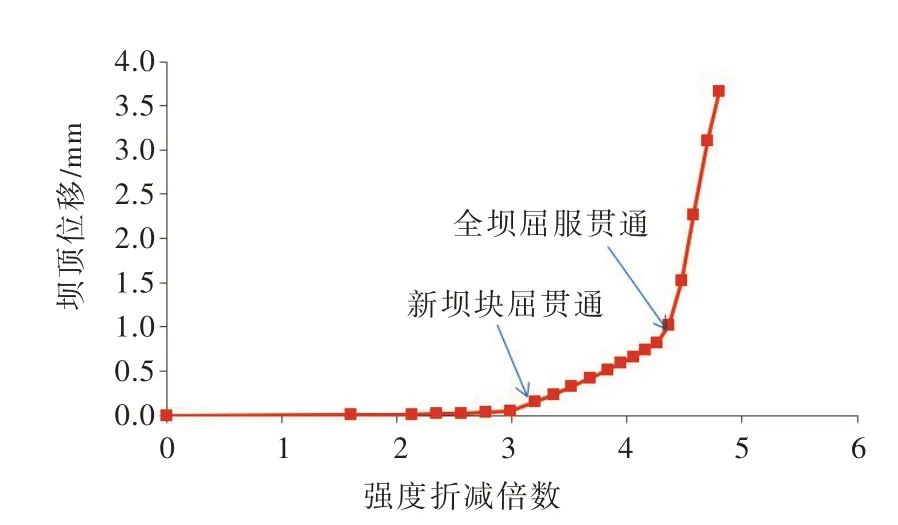
图8 老坝顶位移与强度折减倍数（沿滑动面的摩尔-库仑准则）

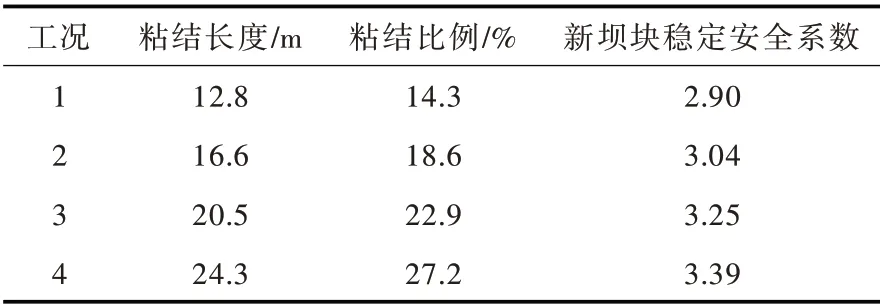
表5 贴坡段下部粘结比例对抗滑稳定安全系数的影响

4.6 丹江口35#坝段及里畈重力坝加高工程的计算结果

4.6.1 丹江口35#坝段 35#坝段为丹江口左联转弯坝段，是大坝左岸最高的典型非溢流坝段。其右侧连接厂房坝段，平面上为上游宽下游窄的梯形，上游宽度21.74 m，圆心角8°1′4″。加高前老坝下游坝坡1∶0.9，加高后下游坝坡1∶0.95。特征高程、水位，计算参数，计算工况等同7#坝段。采用有限元直接反力法计算新老坝块底部的等效内力，进一步求出等效应力法和抗滑稳定安全系数。斜坡段下部结合范围20%时的应力和稳定计算结果见表6。

表6 丹江口35#坝段应力和稳定计算结果

4.6.2 杭州里畈大坝加高 位于杭州的里畈重力坝目前坝高72.0 m，计划加高35.0 m 至坝高107 m。坝顶高程由目前的242 m 提升至277 m，正常蓄水位由234.7 m 提升至265 m，设计洪水位由239.26 m 提升至275.8 m。大坝加高拟采用后帮式，加高前下游坝坡为1∶0.73，加高后坡度为1∶0.75。采用与丹江口35#坝段相同的计算方法得到的典型坝段应力和稳定安全系数见表7。

表7 杭州里畈大坝加高应力和稳定计算结果

由丹江口和里畈两个工程的典型坝段的计算结果可以看出，当新老混凝土结合面的结合状态处于较恶劣状态，即仅斜坡段下部粘结且比例达到20%时，坝体应力和局部及大坝整体抗滑稳定安全系数均满足现行重力坝规范的规定。

5 结论和建议

后帮式加高重力坝，由于新老混凝土材料特性差异、温度变化等因素影响新老混凝土结合面的粘结状态，坝体的应力和稳定如仍按与整体一次浇筑大坝的相同方法计算将会带来较大误差。本文介绍了考虑不同结合面状态的坝体应力分析的有限单元法和稳定分析的强度折减法，提出了新老坝体应力和稳定计算的等效内力法，以丹江口7#坝段为例计算了不同结合面粘结状态时的应力分布和稳定安全系数，得到如下几点结论：（1）有限元等效应力法可以考虑结合面脱开、新老混凝土材料差异、基础非均质性等复杂条件，同时可消除坝踵、新老坝趾处的应力集中，具有有限单元法和材料力学法双方的优势。等效内力的计算可通过应力积分法和直接反力法实现，由于直接反力法从平衡方程得到内力，可以避免网格剖分、应力集中点、应力跳跃点等带来的误差，是大坝加高应力和稳定分析的优选方法。（2）新老结合面粘结不良时会影响新老坝体的分载，稳定分析时除了需要计算整体抗滑稳定安全系数，还应复核新老坝块的局部安全系数，分析方法可用有限元等效内力与刚体极限平衡相结合的方法。（3）弹塑性有限元强度折减法可用于加高重力坝的整体和局部抗滑稳定分析，局部和整体安全系数的取值可通过滑动面贯通和位移曲线拐点对应的折减系数确定。为了便于和刚体极限平衡法比较，采用的计算模型和屈服准则应尽量和刚体极限平衡分析一致。（4）丹江口大坝7#坝段的计算分析结果表明，结合面状态对坝踵应力影响较小，但对建基面新老混凝土结合处的应力影响较大，当斜坡段下部粘结时建基面不会出现拉应力且压应力满足规范要求，粘结比例大于17.5%时抗滑稳定安全系数满足规范要求。丹江口大坝已蓄水运行8年，实测结合面粘结比例大于42%，安全是有保障的。（5）采用如上方法进行应力和稳定分析时，坝体及坝基应力、整体和新老坝块的局部抗滑稳定安全系数的控制标准应与现行《混凝土重力坝设计规范》（SL 319—2018）一致。三维弹塑性有限元的屈服准则及抗滑稳定控制标准、自重作用下的剪应力影响、新老混凝土温差作用等问题仍有待进一步研究。