耦合ALO-LSTM和特征注意力机制的土石坝渗压预测模型

王晓玲，李 克，张宗亮，余红玲，孔令学，陈文龙

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650051）

1 研究背景

大坝渗流安全监测是保证大坝安全稳定运行的重要手段，渗压实时监测数据是大坝运行性态的直接表征［1-2］。目前常用的大坝渗压预测模型主要注重渗压效应量和影响因子之间的非线性映射关系，缺乏对渗压效应量内在影响机制的挖掘。因此，建立精确的渗压预测模型并且探究渗压变化的内在原因，对于深入研究大坝渗流安全状态具有重要的理论和现实意义。

近年来，随着人工智能技术的不断发展，越来越多的机器学习模型应用到大坝渗流预测模型的研究中［3-4］。例如，Chen 等［5］建立了基于最小二乘支持向量机的大坝渗流预警模型。Qiu 等［6］利用小波神经网络和最大熵原理对某土石坝在暴雨影响下的渗流状态进行了研究。Roushangar 等［7］建立了基于小波互信息和高斯过程回归的组合模型来预测土石坝的渗流流量值。Fernando 等［8］将回归树模型应用到大坝异常检测中去。缪长健等［9］、Zhang 等［10］和黄振东［11］针对传统的统计模型难以反映大坝渗流与影响因子之间的非线性关系的缺点，将反向传播神经网络应用于渗流预测模型，提高了模型的非线性映射能力。Chen 等［12］提出了基于核极限学习机渗流预测的数据挖掘与监测框架。冯春燕等［13］建立了卡尔曼滤波回归模型对测压管水位进行预测。Li 等［14］等基于灰色聚类分析方法对用于大坝健康监测。

上述研究在大坝渗流安全监控中发挥了重要的作用。随着人工智能的快速发展，将深度学习模型应用于大坝监测领域已成为研究热点［15-16］。与传统的机器学习方法相比，深度学习模型可对渗流监测数据进行深度挖掘，能得到更加准确的预测结果。在时序预测研究中，循环神经网络（Recurrent Neural Networks，RNN）是一种常用的深度学习模型。然而，RNN 存在梯度消失和爆炸的问题，导致对长时间序列数据的预测精度不足［17］。LSTM 的提出解决了传统循环神经网络（RNN）的缺陷，它在RNN 的隐含层中引入“门”的概念来增强模型的长期记忆能力，可以有效避免时间序列中长期依赖的问题［18］。与其他神经网络模型一样，LSTM 具有众多超参数且难以通过人为选择确定最优超参数。此外，不同的超参数对模型的拟合优度、收敛速度等都存在较大的差异性。蚁狮优化算法（Ant Lion Optimizer，ALO）因其具有调节参数少、收敛速度快、鲁棒性高等特点，在工程领域应用广泛［19-20］。因此，本文采用ALO 算法对LSTM 的参数进行自动寻优。

在大坝服役期间，坝体渗流压力受到上下游水位、温度、降雨以及坝体材料的时变特性等多种变量的耦合影响［2］。由于LSTM 为黑箱模型，故其对坝体渗流压力与影响因子之间的可解释性不高［21-22］。注意力机制是从人类视觉研究中衍生出来的智能算法，通过在关键信息上分配注意力权重来突出重要的特征信息［23］。本文在渗压预测模型中引入一种特征注意力机制以增强模型对各个影响因子的可解释性。值得注意的是，当影响因子维数较多时，会存在多重共线性，不仅会造成信息的冗余［5，24］，还会影响注意力机制进行特征学习时的准确性。因此，在渗压预测研究中需要对影响因子进行降维处理以消除其多重共线性。常用的降维方法有皮尔逊相关分析法、主成分分析（Principal Component Analysis，PCA）、逐步回归、关联度分析方法等［25-26］。其中，PCA 方法是一种通过线性空间变换将多个输入向量进行降维的统计分析方法，其降维效果显著，故本文选择PCA 方法来对各影响因子数据进行降维处理。

综上所述，为深入探究渗压效应量变化的内在影响机制，本文提出了一种耦合ALO-LSTM 和特征注意力机制的土石坝渗压预测模型。首先，为了消除影响因子之间的多重共线性，采用PCA 方法对影响因子进行降维；其次，由于渗压监测数据为时间序列数据，为挖掘其在时间维度上的关联性，构建基于LSTM 的土石坝渗压预测模型，并采用ALO 算法对LSTM 模型的超参数进行自动寻优；最后，采用特征注意力机制量化各个影响因子对渗流压力的影响程度以增强模型的可解释性。

2 耦合ALO-LSTM 和特征注意力机制的土石坝渗压预测模型

2.1 ALO-LSTM 模型与传统的神经网络不同，传统循环神经网络（RNN）借助其循环模块可以帮助模型记忆历史信息，这样网络可以更好地挖掘渗压输入变量和其影响因子中的时间信息。LSTM 模型是对传统循环神经网络的一种改进，它通过将门控制函数引入状态动力学，解决了传统循环神经网络中常见的梯度消失和爆炸问题［27］。LSTM 模型先通过遗忘门从记忆单元细胞中筛选渗压输入变量；其中重要信息的存储由输入门来确定；最后通过输出门来输出渗压变量。LSTM 神经网络的结构示意图如图1 所示。

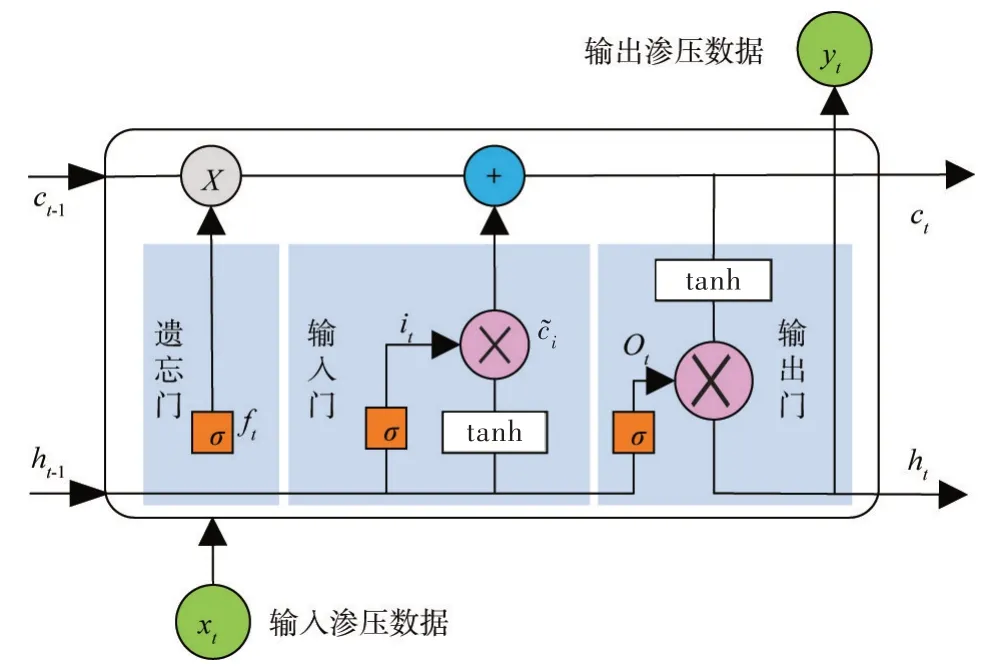
图1 LSTM 神经网络结构示意图

LSTM 结构单元内部的遗忘门、输入门和输出门的建模流程如下：

（1）遗忘门控制从前一刻的记忆细胞中可以积累多少渗压监测数据到当前时刻的记忆细胞中，表达式如下式：

（2）输入门将LSTM 的当前记忆和长期记忆结合起来，形成一个新的单元状态用来挖掘渗压监测数据中的时序特征：

当前时刻单元Ct的状态如下式所示：

（3）LSTM 的最终输出由输出门和单元状态决定：

式（1）至式（6）中：ht-1和ht分别为上一时刻单元的输出和当前细胞的输出；ft、it、、Ct、ot分别为遗忘门、输入门、当前时刻初始细胞状态、当前时刻细胞状态以及输出门的值；σ为Sigmoid 函数；W和b分别为相应的权重系数和偏置项。

由于LSTM 的超参数众多，超参数的选取影响到模型的精度，因此需要合理选择这些超参数。蚁狮优化算法（Ant Lion Optimizer，ALO）是2015年澳大利亚学者Mirjalili Seyedali 受蚁狮捕食行为关系的启发而提出的一种新型群智能优化算法。相关研究表明蚁狮优化算法具有比遗传算法（Genetic Algorithm，GA）、花朵授粉算法（Flower Pollination Algorithm，FPA）和蝙蝠算法（Bat Algorithm，BA）等算法更优的寻优精度和更快的收敛速度［28］。

ALO 算法具体的操作流程如下：

（1）蚂蚁随机游走。在自然界，蚂蚁通过随机游走的方式来寻找食物，如式（7）所示：

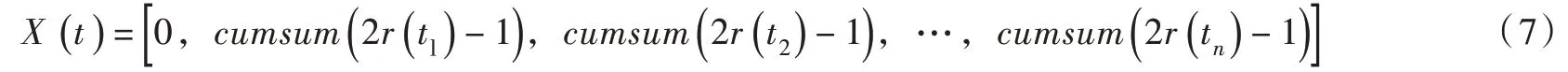
式中：cumsum为累积和；t为蚂蚁在随机游走时的位置；n为最大迭代次数；r(t)为蚂蚁在游走过程中产生的随机数，可由下式生成：

（2）蚂蚁游走范围。蚁狮构造的陷阱会影响蚂蚁的随机行走，其数学模型表示如下：

式中：Antlionjt为蚁狮在第t次迭代时第j只的位置；d it为所有输入向量在第i个蚂蚁中的最大值；c it为所有输入向量在第i个蚂蚁中的最小值；d t为所有输入向量在第t次迭代时的最大值；ct为所有输入向量在第t次迭代时的最小值。

（3）蚂蚁掉落陷阱

式中I为比率。

（4）蚁狮重构陷阱。为了使捕捉新蚂蚁的机会增加，蚁狮需要通过改变自己的位置来适应被捕食蚂蚁所在的位置，由下式表示：

式中Ant it为第i只蚂蚁在第t次迭代时的位置。

（5）精英化蚁狮。在每一次迭代的过程中，适应度最好的蚁狮所在的位置会被留下来当做精英蚁狮，精英蚁狮在迭代过程中能影响蚂蚁的位置。可根据下式得到蚂蚁的位置：

式中：R At是在第t次迭代中根据轮盘赌机制选择蚁狮的随机游走策略；R Et是第t次迭代中围绕精英蚁狮的随机游走策略。

ALO 算法具有调节参数少、收敛速度快、鲁棒性高等特点，该算法采用随机游走以及轮盘赌方式等策略可有效避免陷入局部最优等问题。本文使用ALO 算法优化LSTM 模型超参数，可以快速找到最优超参数的组合，避免手动调参带来的不便，提高模型训练效率。

2.2 特征注意力机制特征注意力机制作为一种增强局部特征学习的思想，它不是一种固定的神经网络结构［29］。引入特征注意力机制目的在于通过调整注意力权重，从输入向量的大量信息中快速提取有效信息。由于特征注意力机制能够自适应地集中于特征的有效部分，因此被广泛应用于图像分类［30］、神经机器翻译［29，31］、时间序列预测［32］等研究领域。本文中引入特征注意力量化渗压效应量与各输入变量之间的关联关系。特征注意力机制的表达式如下：

式中：Wa为注意机制的权值矩阵，表示需要强调的信息；et为第一次加权计算结果；b为注意力机制的偏置项；[X1，X2，…，XT]为输入项；at为输入项得到的最终权重。

对于渗压预测模型，通常的手段是选用高精度的机器学习或深度学习模型进行预测，但是却忽略了哪些影响因素对渗压效应量的影响程度最大。本文所提的渗压预测模型引入特征注意力机制计算隐含层单元状态的特征权重，根据权重分配原则计算不同单元状态的特征权重参数来表征渗压效应量与各个影响因子之间的相关关系，并通过softmax 函数得到和为1 的权重分布矩阵。

2.3 耦合ALO-LSTM 和特征注意力机制的土石坝渗压预测模型建模流程本文所提模型的建模流程如图2 所示，主要包括以下4 个步骤：

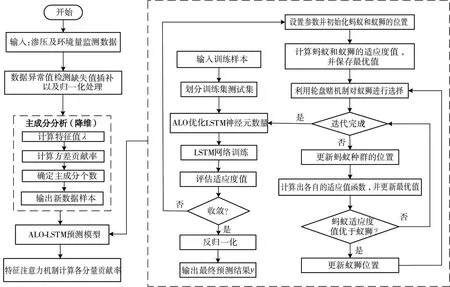
图2 耦合ALO-LSTM 和特征注意力机制的土石坝渗压预测模型建模流程

（1）将获取的渗压监测数据和环境量监测数据进行异常数值检测、缺失值插补和归一化处理；

（2）对输入变量进行降维处理，并划分训练集和测试集；

（3）通过LSTM 网络构建预测模型，其中输入层和输出层的神经元数量使用ALO 优化算法来自动寻优；

（4）通过特征注意力机制对输入变量赋予不同的权重量化渗压与影响因子的关联关系，并将输出向量进行反归一化处理获得渗压最终预测结果。

3 案例研究

本研究选用澜沧江下游某砾石土心墙堆石坝工程的渗压计监测数据为研究对象，该工程坝顶高程821.5 m，建基面高程为560 m，具有防洪、发电等综合效益。在本文中，选取渗压计DB-C-P-01 处监测点建立预测模型进行分析，建模序列选取2014年7月15日至2018年7月31日，取值频率为天。

图3 表示该处测点在该时间段中渗压观测值，以及对应的上游水位、降雨量的历时过程线。

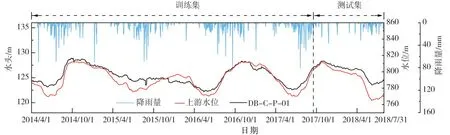
图3 渗压观测时间历程

3.1 初始输入变量选择大坝渗压水头主要受上下游水位、温度、降雨以及坝体材料的时变特性等影响。大坝渗压效应量表示如下：

式中δ、δH、δT、δp、δθ分别为渗压效应量、水位分量、温度分量、降雨分量和时效分量。

（1）水库水位变化对坝体渗流影响较大，并有一定的滞后效应，其中等效水位可按照平均水位的方法计算，以表示渗流的滞后效应［2，33］。水位分量可表示如下：

式中：hu为当天的上游水位，m；为前1 ～3 天上游水位均值，m；为前4 ～7 天上游水位均值，m；hd为当天的下游水位，m。

（2）温度分量是指基岩和大坝坝体的温度变化从而引起的渗流变化。坝体和基岩的温度随大气温度呈周期性变化，一般采用周期函数表示。本文中选择多周期谐波函数作为温度的表征因子，如下式所示：

式中：i=1，2；t为从起始日到实测日的累计天数，d。

（3）降雨分量也是影响大坝渗流的一个主要因素，其对渗压水头的影响机制较为复杂。一部分由降雨入渗直接影响；一部分降雨直接形成地表径流汇入河道使库水位升高从而影响渗压的变化［34］。本文中采用主成分分析方法进行降维避免了降雨分量和水位分量之间的相互影响，所以这里的降雨分量主要集中在降雨入渗的影响上。降雨分量可由下式表示：

式中：p为当天的降雨量， mm；为前1 ～3 天降雨量均值， mm；为前4 ～7 天降雨量均值， mm。

（4）时间分量是一个不可逆的分量，随着时间的推移，它以不可逆的方向发展。主要反映了坝体材料蠕变、坝基岩石蠕变、岩体节理裂缝、软弱结构对渗压的影响。一般情况下，时间分量的变化在开始时变化剧烈，在后期逐渐趋于稳定。时效分量的一般变化规律可以用下式表示［2，35］：

式中θ为模型起始日至实测日的天数除以100。

综上所述确定土石坝渗压预测模型的初始影响变量为：

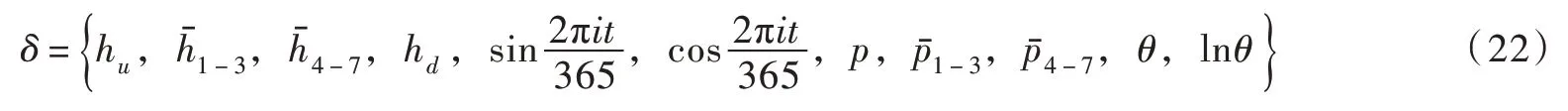
3.2 主成分降维PCA 通过空间变换将一组含有相关性的数据重构成n个几乎线性不相关的向量，可以解决大坝渗流预测中由于输入向量维数过多而存在的多重共线性问题，进而提高模型的预测精度。对3.1 节提到的影响因子进行降维处理，得到如表1所示的方差累积贡献率。方差累计贡献率达到85%以上就可以认为所得到的主成分可以解释原始影响因子的大部分信息。

表1 方差累积贡献率

经PCA 计算得到表1的方差累积贡献率，从表1可以看出前五个主成分的累积方差达到了87%，因此通过计算将原始数据为11 维的向量重构成5 个主成分，即消除了多重共线性又大大降低了输入向量的维度。表2为各主成分分量的得分系数矩阵。

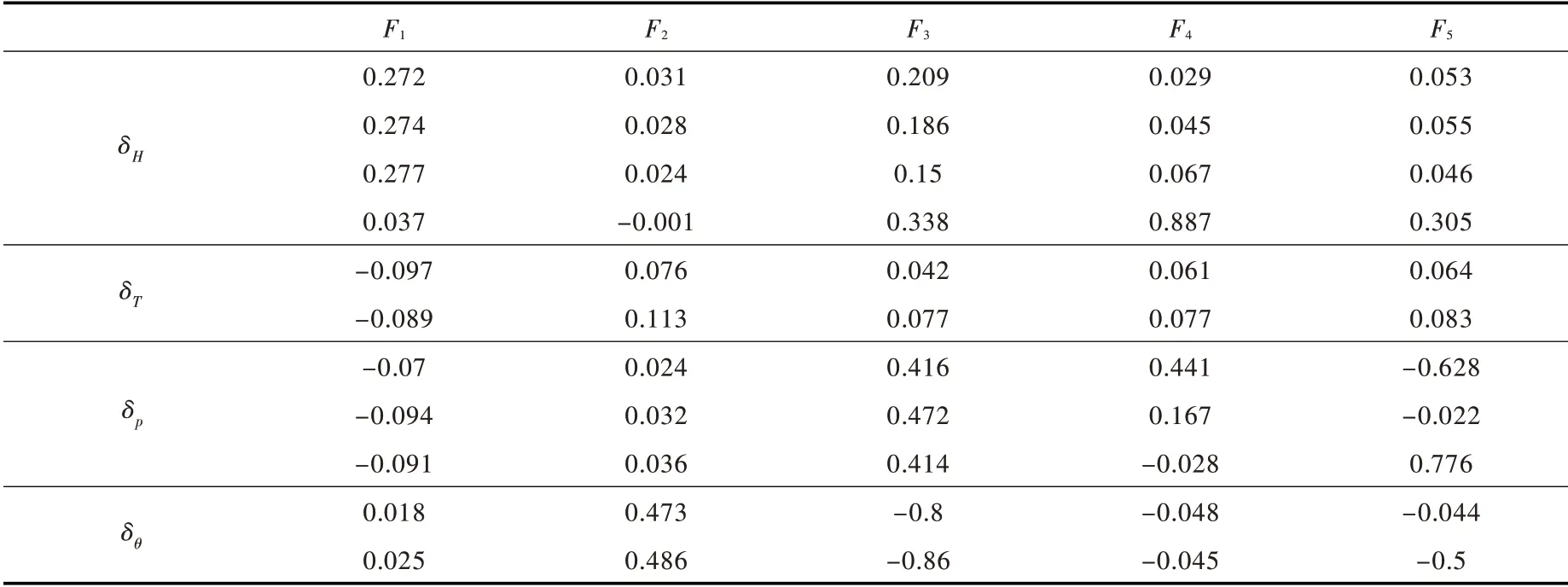
表2 主成分分量得分系数表

3.3 ALO-LSTM 和特征注意力机制算法的土石坝渗压预测

3.3.1 模型参数和预测性能指标确定 首先LSTM 本身的参数有输入层神经元个数L1、输出层神经元个数L2、学习率ε、最大批数E、时间步长T，这些参数对模型的精度有重要的影响。其中ALO 算法对两层的神经元个数L1和L2进行自动参数寻优，其中ALO 算法种群规模设为50，最大迭代次数设为100，另外学习率设为0.01，时间步长设为6，最大批数设为32。

在本文中，引入平均绝对百分比误差（MAPE）、均方根误差（RMSE）、平均绝对误差（MAE）来反映模型的预测效果，以上三个指标参数越小，表明模型的预测效果越好：

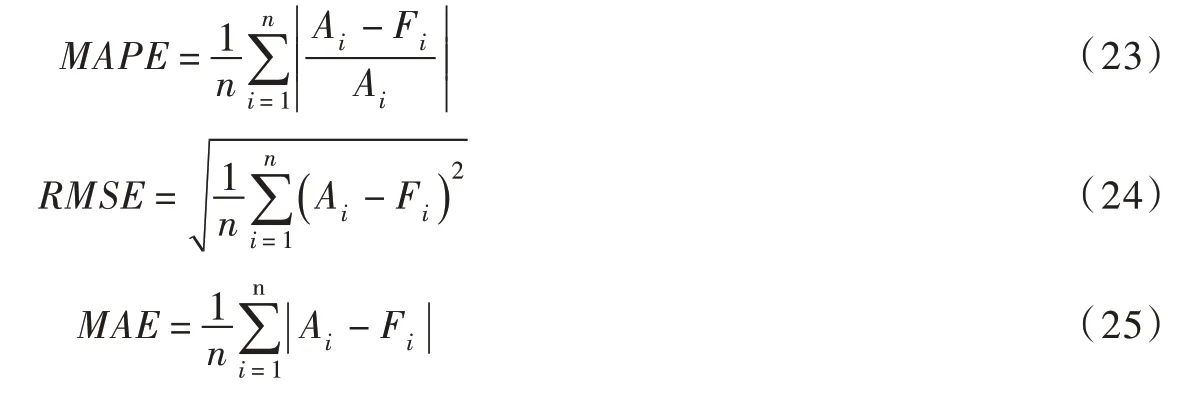
式中：n为样本个数；Ai为监测值；Fi为预测值。

3.3.2 大坝渗压预测结果和影响机制分析 运用本文模型对坝体渗压计DB-C-P-01 处监测点进行预测，模型拟定测试集为2017年9月18日至2018年7月31日，预测结果如图4 所示。

从图4 中可以看出，预测值与实测值的拟合程度较高，其R2达到了0.98 以上。进一步地，测试集的预测性能指标MAPE、RMSE和MAE分别为0.28%、0.022 m、0.17 m。由此可见，本文所提模型的精度较高。

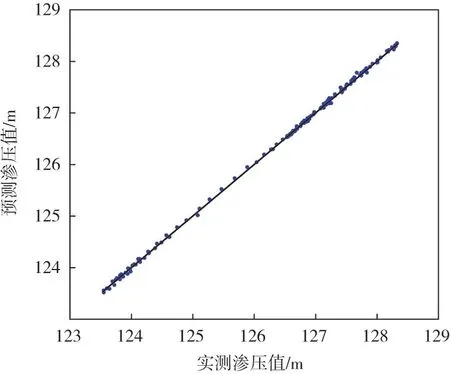
图4 测点DB-C-P-01 实测值与预测值关系图

通过特征注意力机制可以得到各个输入向量即主成分分量的影响程度占比，结果如图5 所示。

从图5 可以看出，F1占比最大，为41.1%，F2占比最小，为6.31%。主成分分量是通过原始影响变量的线性变换得到的，所以可以通过主成分得分系数矩阵进行归一化计算得到各个分量的贡献率。各影响分量的权重如图6 所示。

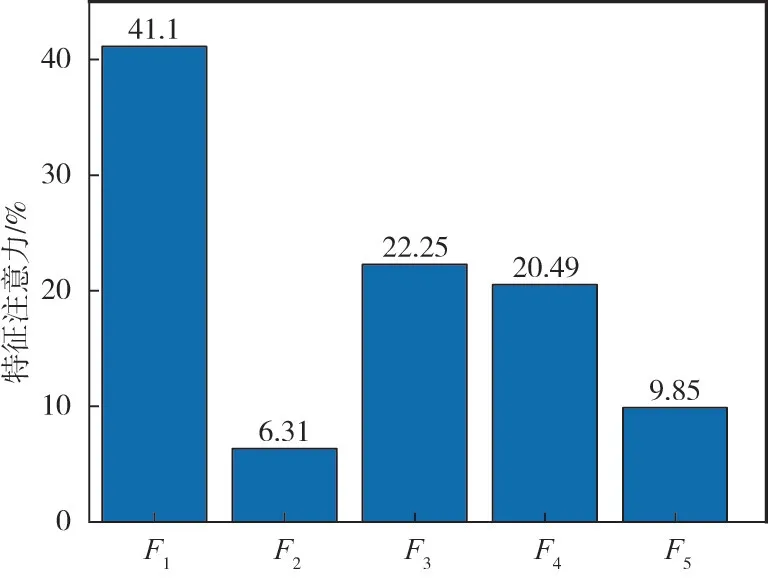
图5 各主成分权重计算结果

从图6 中可以看出，该测点的渗压水位分量影响较大，占比达到47.9%，其次是降雨分量，占比达到33.5%。温度分量和时效分量对坝体渗压水位的影响程度较小，比重都在10%以下。

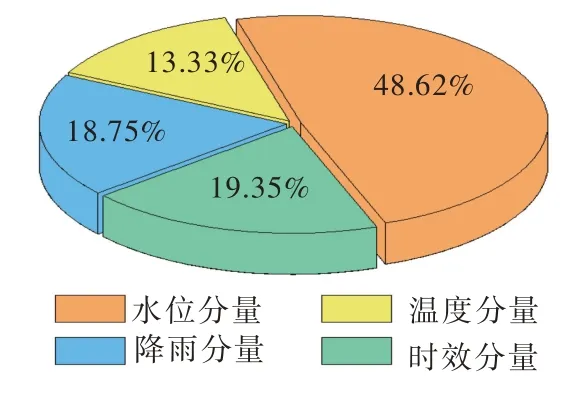
图6 各个影响分量的权重

4 模型对比分析

为验证本文所提模型的优越性，本文选择BP 神经网络、LSTM 、LSTM-Attention 与本文所提模型进行对比分析。图7 显示了上述4 个模型在DB-C-P-01 测点的预测结果。从图7 中可以看出，本文所提模型预测结果更接近渗压实测值。相比于其他三种基于LSTM 的预测模型，BP 神经网络的拟合精度较差，说明LSTM 算法更能挖掘渗压监测数据的时序信息。LSTM 模型在2018年4月到7月期间的精度要劣于其他模型，这是由于LSTM 模型本身为深度学习模型需要大量数据支持，当数据量过少时会出现模型过拟合的现象。LSTM-Attention 和本文模型的稳定性较高，由此可以看出加入注意力机制可以加强对局部特征信息的挖掘。

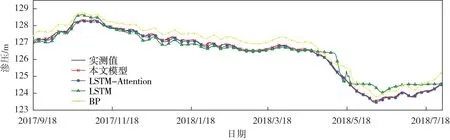
图7 4 种模型的预测结果对比

图8 所示的是4 种模型的预测性能指标统计结果。从图8 可以看出，本文提出的模型具有更高的预测精度，RMSE、MAE、MAPE值分别为0.28%、0.022 m、0.17 m。相比于LSTM-Attention、LSTM和BP 三种模型，其RMSE分别提高62.67%、91.36%和93.32%；MAE分别提高64.52%、91.06%和94.57%；MAPE分别提高62.5%、91.05%和94.69%。

图8 4 种模型的预测性能指标

5 结论

大坝渗压预测对大坝安全管控具有重要意义。本文综合考虑大坝渗压效应量存在的时序特性和多因子影响特性，构建了耦合ALO-LSTM 和特征注意力机制的土石坝渗压预测模型，得到了如下成果：

（1）针对目前输入向量构建复杂，且存在严重的多重共线性，采用PCA 算法对影响因子进行降维，将原始11 维输入向量重构成5 维向量，从而消除了原始输入向量中存在的多重共线性。

（2）提出了耦合ALO-LSTM 和特征注意力机制的预测模型，通过ALO 算法对LSTM 的超参数进行优化有效解决了人工调参困难的问题，并通过特征注意力机制计算各个主成分分量的权重，增强了模型对输入向量的可解释性。

（3）以西南某土石坝为案例研究，预测结果显示渗压测点的水位分量占比最大，降雨分量次之，符合工程实际。对比分析表明，本文所提模型相比于LSTM-Attention、LSTM、BP 神经网络具有更高的预测精度，其RMSE、MAE、MAPE值分别为0.28%、0.022 m 和0.17 m。