基于IGBT选型的整流器、逆变器损耗计算新方法研究

张成明，陈德志，赵文良

（1.沈阳工业大学，辽宁沈阳 110870；2.山东大学，山东济南 250100）

0 引言

随着社会对于环境问题的日益关注，以风能、光伏为代表的可再生清洁能源受到重视，在此基础上，近年来我国关停了一些小型火电站，并积极推进新能源的发展和使用，实现“双碳”目标[1]。电机生产过程中耗电量大，变频器可以帮助企业节能减排。绝缘栅双极型晶体管（Insulate Gate Bipolar Transistor，IGBT）具有电力场效应管（MOSFET）和电力双极型晶体管（GTR）的优点，一经问世就迅速成为主流的控制器件。目前将多个IGBT 芯片按一定的电路连接起来，使用绝缘树脂封装，成为IGBT 模块的主流发展方向。IGBT 模块向着功率密度更大、体积更小、高频化和集成化不断发展[2]。在这个趋势中IGBT 模块需要承受更大的温度及应力，将加速材料的疲劳、失效。引起器件失效的原因很多且复杂，在这些原因中占比重较大的有环境应力、长时间过载、系统暂态、制造工艺的瑕疵和功率/温度冲击[3-9]。

IGBT 器件的热失效根本原因为器件在工作过程中热量累积使温度到达非安全工作区，导致器件的永久性损伤[10-14]。所以，损耗和散热一直是影响IGBT 选择和合理设计并优化散热器的重要基础[15]。

通常情况下，IGBT 模块制造厂商会为用户提供损耗计算软件，但是这些损耗计算软件大多采用简单的热电路模型来绘制损耗曲线和结温曲线，用于计算指定工况下功率器件的平均损耗和功率器件的结温时存在着一些缺陷，例如拓扑结构不完整、产品数据不全、设计的算法与实际工况匹配度差等情况。文献[16]利用Simplorer/Simulink 联合仿真计算出IGBT 损耗，模型符合实际，误差更小。文献[17]中提出了基于较少参数简化计算IGBT 损耗的方案，虽然有效性得到一定保证，但是准确性较差。文献[18]根据IGBT 基本损耗计算公式，利用热阻计算IGBT 的温度，但是这种计算方法只考虑导通损耗和开关损耗，并没有考虑到栅极电阻和直流母线电压对计算的影响，导致计算值和实际温度存在较大误差。文献[19]中提出一种基于热传导模型的IGBT 结温计算方案，可以实现IGBT 芯片结温的快速计算。文献[20]中提出了一种抛物线插值法来计算逆变器IGBT 损耗的方法，经实验验证，计算结果和实际情况贴合，误差在4%以内。

文献[21-23]对IGBT 的损耗进行了详细计算，分析了损耗、结温和输出电流的关系并得出相关结论。本文在分析IGBT 基本损耗的同时，综合考虑栅极电阻、直流母线电压对功率器件损耗和温度的影响，准确计算了可控整流和逆变器中的IGBT 损耗、结温和散热器温度，为IGBT 的选择和散热器的设计提供了依据。通过仿真及实验验证了该方法在IGBT 损耗计算、选择以及散热器设计中的正确性。

1 IGBT模块选型

可控整流和逆变器IGBT 模块的选择主要取决于电压等级、电流和发热情况。由于发热量与IGBT型号有关，因此必须对IGBT 进行预选择。

通常，在IGBT 模块选型中忽略电源模块的结温和散热器温升。本文所述方法综合考虑了电源电压、电流、过载、散热器温升、功率模块结温等因素，可在一定程度上提高计算的精度与器件选择的合理性。变频调速系统的拓扑结构如图1 所示，其基本参数见表1。图1 中，S1—S6代表6 个整流用IGBT，SA，SB，SC，Sa，Sb，Sc为逆变器用IGBT，C 为直流母线电容。

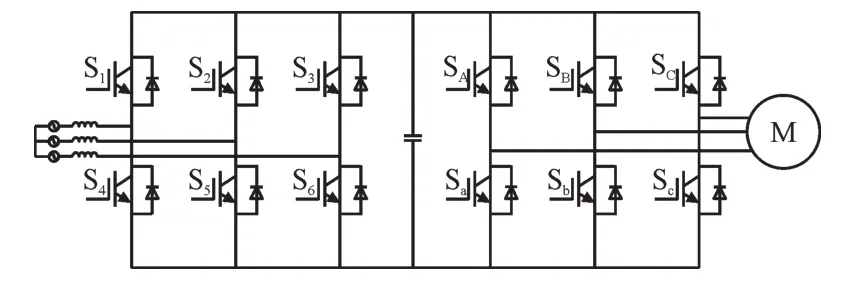
图1 调速系统拓扑Fig.1 Topology of speed control system

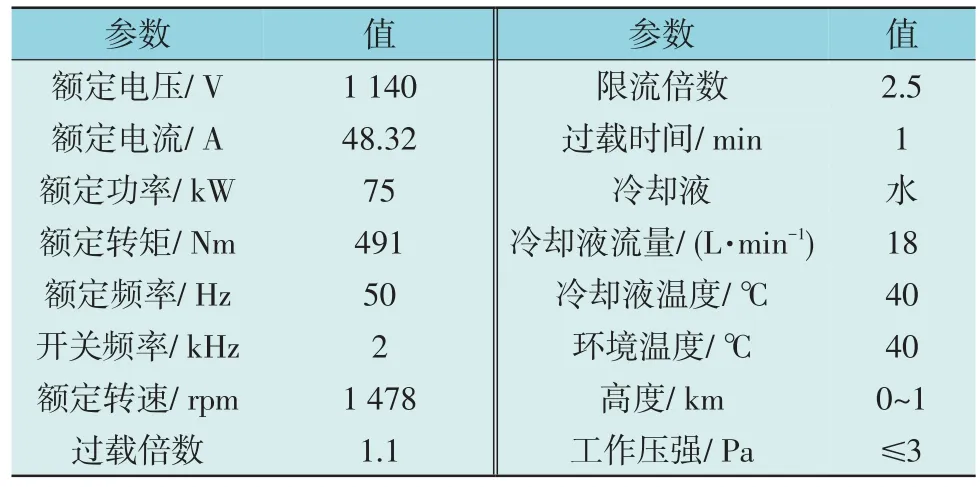
表1 调速系统基本参数Table 1 Basic parameters of speed control system

流过IGBT 模块的过载峰值电流和最大峰值电流可以表示为：

式中：Iovd_peak，Iovc_peak分别为流过IGBT 模块的过载峰值电流和最大峰值电流；Kovd，Klim分别为过载倍数和最大极限电流倍数；IN为额定电流。

为保证功率模块满足温升要求，根据经验，通常要求长时间的过载电流峰值低于IGBT 的额定集电极电流，短时过载电流低于IGBT 重复峰值集电极电流，即：

式中：IC，ICRM分别为额定集电极电流和重复峰值集电极电流；Iovd_peak_longtime，Iovd_peak_shorttime分别是长期和短期过载峰值电流。

同时，电流的最大峰值不应超过IGBT 的集电极电流峰值，以免发生意外。

当工作在逆变器中时，可以计算出母线电压的最大值VDC_inv_max为：

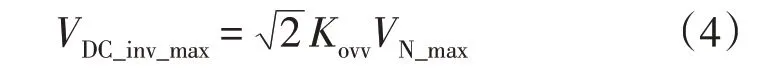
式中：Kovv为波动系数；VN_max为最大输入电压。

当逆变器处于制动状态时，逆变器回馈的能量使得母线电压升高，制动电压准位会高于逆变时的工作电压，由于不需要电能回馈所以直流母线电压过压点必须高于制动电压准位，二者的关系为：

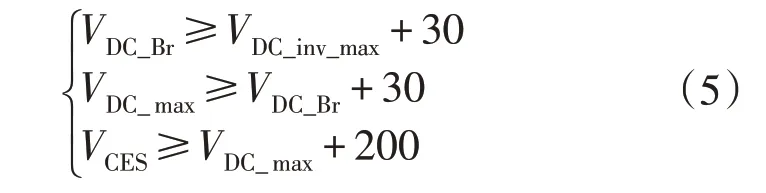
式中：VDC_Br为制动电压准位；VDC_max为直流母线过压点；VCES为IGBT 的额定电压。

根据式（5），IGBT 的电压选择条件为VCES≥2 307.2 V。查询IGBT 手册，IGBT 功率模块型号可以初步选定为Infineon 公司的FF200R33KF2C。

2 散热器热阻、可控整流器损耗和温升的计算

2.1 散热器热阻计算

热阻表征导热过程中的阻力，是反映阻碍热量传递的综合参量，为了简化计算，认为散热器在冷却过程中只存在对流换热和导热换热2 种传热过程，忽略热辐射[24]。即散热器只存在对流换热热阻和导热热阻。水冷板导热热阻Rnd计算公式为：

式中：K为散热器材料的热导率；L为散热器的厚度；A 为散热器垂直热流方向的面积。

散热片与散热器内水之间的对流换热热阻Rnv为：

式中：Dh为传热面的几何特征长度即管道直径；Nu为努塞尔数；λf为流体导热系数；As表示总的有效对流换热面积。

散热器总热阻R计算公式如下：

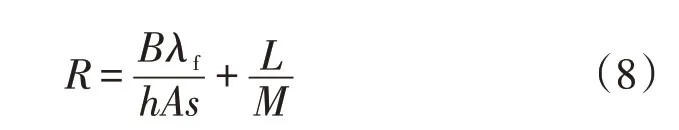
式中：B为散热器的宽度；h为液体强制对流换热系数，它和努塞尔数有关；M为散热器的长度。

2.2 可控整流器损耗计算

可控整流器主要由IGBT 和反向并联整流二极管组成。整流器的损耗主要是由IGBT 和二极管的导通损耗和开关损耗组成，如（10）所示。

式中：Pcon_IGBT为IGBT 导通时产生损耗；Pcon_Diode为二极管导通过程中的损耗；VF(t)为二极管的导通电压；VCE(t)为IGBT 的导通电压；IC(t)为IGBT 的电流；IF(t)为二极管的电流；DQ(t)为IGBT 的占空比；DD(t)为二极管的占空比；T为调制波的周期；PSW_IGBT为IGBT开关过程产生的损耗；PSW_Diode为二极管开关过程产生的损耗；Eon(ti)和Eoff(ti)分别为在ti时刻器件产生的开通损耗、关断损耗；fSW为开关频率；Erec(ti)为二极管在ti时的反向恢复损耗。

研究表明，IGBT 开关损耗和并联整流二极管的恢复损耗与功率模块采用的开关频率、栅极驱动电阻以及变频器直流母线电压和器件的结温有关。式（11）是开通、关断过程产生的损耗以及Diode 的反向恢复损耗的修正系数，式（12）是计算IGBT 的开关损耗以及二极管在关断过程中产生损耗的修正函数。

式中：KEon_Tmp为结温的导通损耗修正系数；KErec_Tmp为整流二极管恢复损失的修正系数；KEoff_Tmp为器件结温的关断损耗修正系数；Regress()为Matlab 软件下的曲线拟合函数；Tj为结温；Eon为开通能量损耗；Eoff为关断能量损耗；Erec为反向恢复损耗。

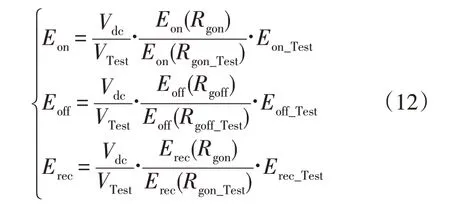
式中：Vdc为母线电压；VTest为IGBT 集-射极电压的测试值；Eon(Rgon_Test)，Eoff(Rgoff_Test)分别为测试过程中IGBT额定电流时门极电阻对应的开通损耗和关断损耗；Eon(Rgon)，Eoff(Rgoff)分别为实际额定电流时门极电阻对应的导通和关断损耗；Eon_Test，Eoff_Test，Erec_Test分别为在测试条件下的开通损耗、关断损耗以及反向恢复损耗；Eon，Eoff，Erec分别为导通一次的损耗、关断一次的损耗和二极管的反向恢复损耗；VTest，Rgon_Test，Rgoff_Test，Eon(Rgon_Test)，Erec_Test和Eoff(Rgoff_Test)可以从功率模块的规格中找到[10]。

在特定结温下可以计算出VCE0（t）0，VCE0（t）1，VF0（t）0，VF0（t）1，Tj_Inv0（t）和Tj_Inv1（t）的值。通过基于导通压降函数和开关损耗函数的插值算法，能够计算出在不同结温下VCE（t），Eon（t），VF（t），Eoff（t）和Erec（t）的函数表达式：

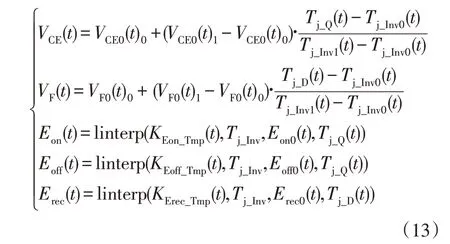
式中：linterp()为Matlab 软件中线性插值函数；VCE(t)是t时刻的集射极电压；Tj_Q(t)，Tj_D(t)分别为IGBT 和二极管的结温；Tj_Inv(t)是逆变器温度。

2.3 温升计算

可以通过热路模型和损耗来计算结温，其中功率损耗相当于电流源，热阻产生的温差相当于电压。图2 是IGBT 的结构和热电路模型。图2 中，Tj，Tc，Th和Tamb分别为芯片的结温、壳温、散热器温度和环境温度；Tjc，Tch，Tha分别为芯片和壳的温差、壳和散热器的温差、散热器和环境的温差；Rthjc，Rthch，Rthha分别为结-壳热阻、壳-散热器热阻和散热器-环境的热阻，PIGBT，PDiode分别为IGBT损耗和Diode损耗。

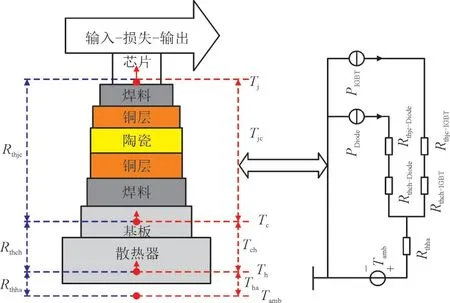
图2 IGBT结构和热路模型Fig.2 IGBT structure and thermal circuit model

式（14）为热量在传递的过程中，热阻、损耗和温差的关系：

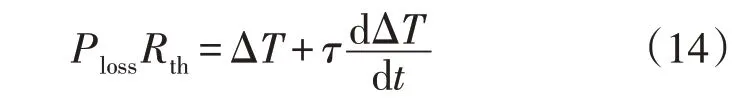
式中：Ploss为能量损耗；Rth为热阻；ΔT为温差；τ为时间常数。

由于损耗函数一般不是规则的曲线，给计算结温造成一定的困难。为了简化计算，将损耗函数假设成理想半正弦波，理想损失可以表示为：

式中：Ploss_tot，Ploss_IGBT和Ploss_Diode分别为一个周期内模块总损耗、IGBT损耗和Diode损耗；TM为开关周期。

将（15）代入（14），微分方程求解如下：

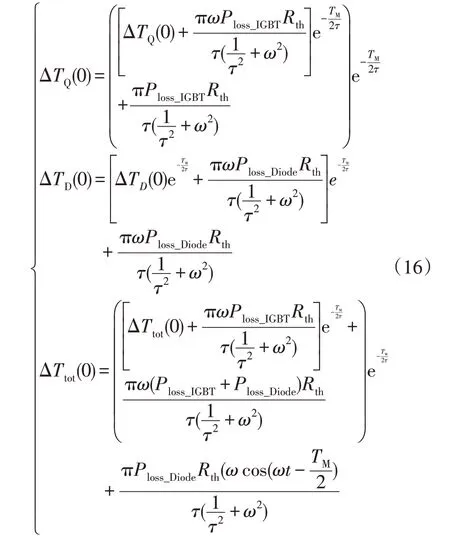
式中：ΔTQ，ΔTD，ΔTtot分别为IGBT 温差、Diode 温差和总温差。

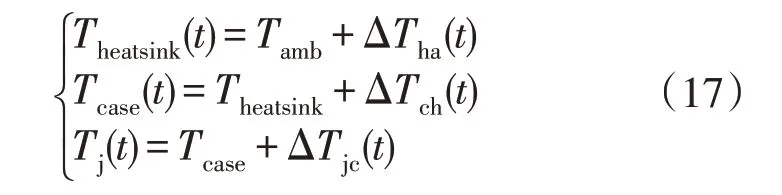
式中：ΔTha（t）为散热器温度和工作环境温度之间的温差；Tcase（t）为IGBT 的外壳温度；ΔTjc（t）为IGBT 芯片的温度和模块外壳温度之间的温差；ΔTch（t）为IGBT 模块的表面温度和散热器温度之间的温差；Theatsink（t）为散热器的温度；Tj（t）为IGBT 的结温。

IGBT 模块的损耗以及结温这2 个变量在计算的过程中相互作用，因此在结温未知的情况下不能准确地计算损耗。为此在计算时假设在初始条件下每个点的温度和环境的温度相等，然后循环迭代计算，得到稳定的器件损耗和结温。最高结温是Tj（t）的最大值。具体损耗计算流程如图3 所示。

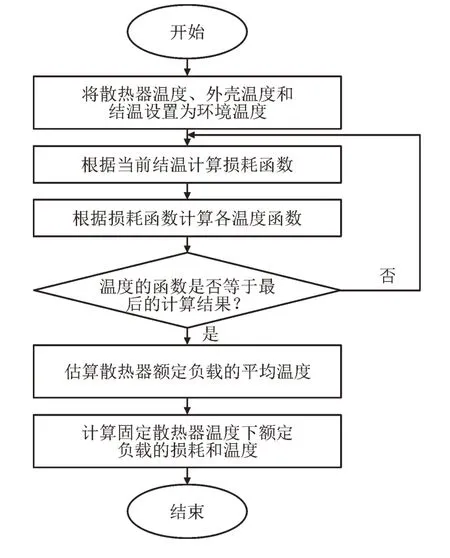
图3 损耗和温度计算流程Fig.3 Process of loss and temperature calculation

IGBT 与反向并联的整流二极管的总损耗均为导通损耗加上开关损耗[12]。

式中：Ptot_IGBT和Ptot_Diode分别为IGBT 和二极管的总损耗。

整流器由3 个桥臂组成，每个桥臂上有2 个开关。每个开关包括1 个IGBT 和1 个反向并联二极管，因此整流器的总损耗PRectifier为：

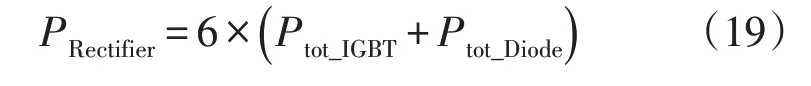
由于IGBT 和二极管的损耗会随着结温的变化而变化，因此在损耗计算中需要对IGBT 和二极管的结温进行计算。IGBT 结温Tvj_IGBT、二极管结温Tvj_Diode、散热器温度Theatsink为：

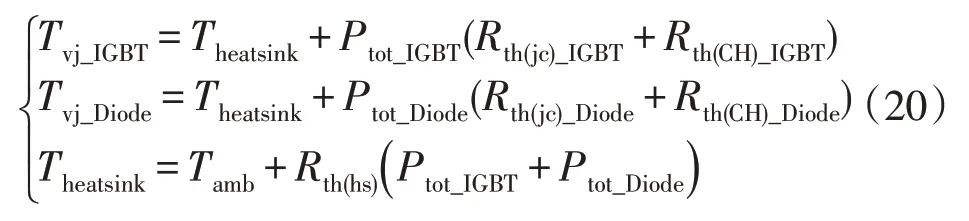
式中：Rth（jc）_IGBT为IGBT 芯片和铜基板之间的热阻；Rth（jc）_Diode为二极管和铜基板之间的热阻；Rth（CH）_IGBT为IGBT 铜基板和散热器之间的热阻；Rth（CH）_Diode为二极管铜基板和散热器之间的热阻；Rth（hs）是散热器和环境之间的热阻。

IGBT 器件的结温和损耗在实际和计算中是相互影响的，因此在IGBT 的损耗计算时，需要先根据式（6）、式（18）、式（19）求出相关损耗。然后，将相关损耗代入到式（20）中，计算出结温和散热器的温度，根据这个温度计算损耗，最后根据重新计算得来损耗修正结温。经过这个计算流程，得到稳定的器件结温以及损耗。计算结果见表2。表2 中Theatsink，Tcase_IGBT,TJ_IGBT,Tcase_Diode和TJ_Diode分别为散热器温度、IGBT 壳温、结温，Diode 壳温、Diode 结温，PRectifier为整流器总损耗。图4 显示了PWM 整流器的温度曲线。

表2 PWM整流器中IGBT温度及损耗计算结果Table 2 IGBT temperature and loss calculation results of PWM rectifier

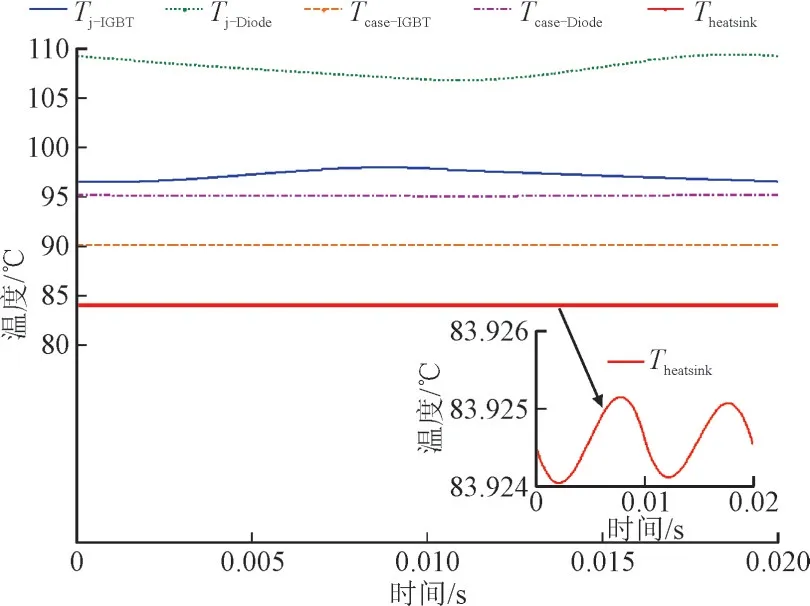
图4 整流器的IGBT温度曲线Fig.4 IGBT temperature curves of rectifier

3 直流母线电压和栅极驱动电阻对损耗计算的影响

考虑到直流母线电压和栅极驱动电阻对计算结果有影响，本文采用的栅极导通电阻为5.6 Ω，栅极关断电阻7.5 Ω。

3.1 直流母线电压对损耗计算的影响

直流母线电压一般控制在1 300～1 760 V，受供电电压波动影响，系统其它的参数无变化。图5 显示了整流器温度和损耗随不同直流母线电压的变化趋势。

图5 整流器温度和损耗随母线电压变化的趋势Fig.5 Variation trend of rectifier temperature and loss with bus voltage

随着母线电压的不断升高，IGBT 模块和并联整流二极管的外壳温度和结温升高，散热器温度升高，但是并联二极管的通态损耗增加较慢。同时，IGBT 和二极管的开关损耗增大，IGBT 的通态损耗增大，整流器的总体损耗增大。

3.2 栅极电阻对损耗计算的影响

栅极导通电阻和栅极关断电阻对功率模块的损耗、温升的计算结果有影响。栅极电阻影响IGBT的开关时间、开关损耗、短路电流安全运行区域、dv/dt、di/dt和二极管的反向恢复电流。因此，栅极电阻必须按照各个应用参数仔细选择和优化。

考虑到1 140 V/75 kW 功率等级用IGBT 的栅极开启电阻经验值一般为2.2～15 Ω，图6 显示了不同栅极导通电阻下整流器温度和损耗的趋势，本文栅极导通电阻设为5.6 Ω。结果表明，栅极导通电阻的选取对于IGBT 模块的损耗和温升有较大影响。

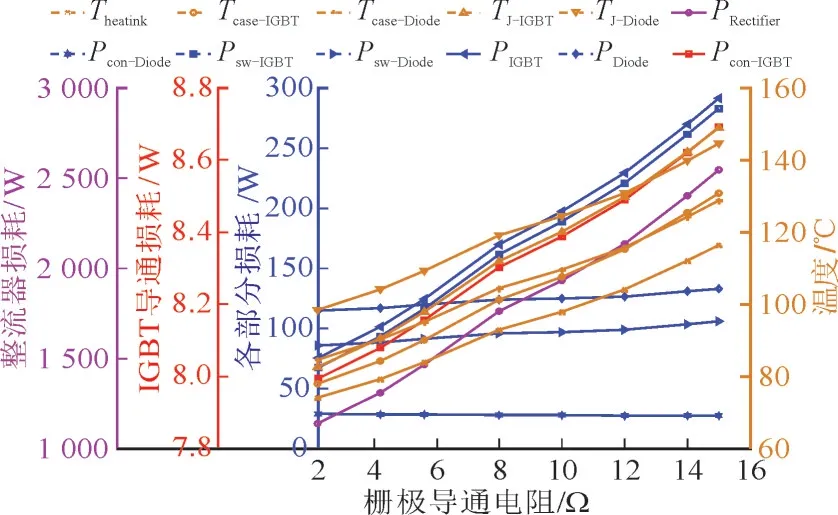
图6 整流器温度和损耗随栅极导通电阻变化的趋势Fig.6 Variation trend of rectifier temperature and loss with gate on-resistance

3.3 栅极关断电阻对损耗计算的影响

考虑到本文使用IGBT 栅极关断电阻经验值为3.7～30 Ω，图7 显示了整流器温度以及损耗在各个栅极关断电阻下的变化。栅极关断电阻对于整流器中IGBT 的损耗以及温升计算结果也有很大影响。

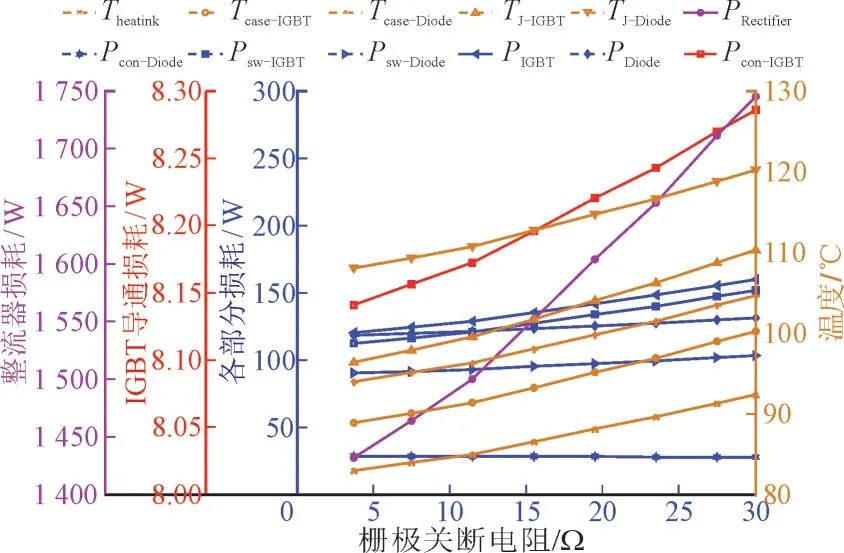
图7 整流器温度和损耗随栅极关断电阻变化的趋势Fig.7 Variation trend of rectifier temperature and loss with gate turn-off resistance

从图7 可知当栅极关断电阻增大时，器件的外壳温度、IGBT 及反向并联二极管的结温都在升高，而并联整流二极管的导通损耗增加得较慢。IGBT芯片以及二极管的开关损耗增加，IGBT 的通态损耗增加，整流器的总损耗升高。

4 逆变器损耗及温升计算

计算逆变器的损耗和温升，其原理与整流器的原理是基本一致的。只是需要将计算程序的功率因数设置为相应的功率因数，并将电流设置为负值。计算结果如表3 所示，表3 中PInverter为逆变器总损耗。图8 为逆变器在1.2 倍额定负载下的结温曲线。

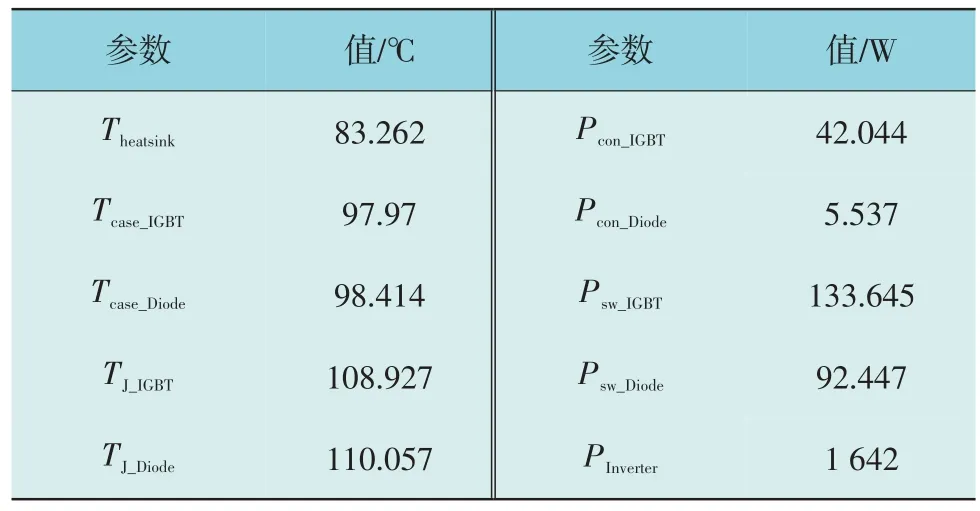
表3 PWM逆变器IGBT温度及损耗计算结果Table 3 IGBT temperature and loss calculation results of PWM inverter

图8 逆变器温度曲线Fig.8 Temperature curve of inverter

通过对PWM 整流器和逆变器的损耗和温升的计算，可以对散热器系统展开设计。

5 整流器和逆变器温升实验

根据整流器和逆变器的损耗计算，设计散热器。调速系统功率部分的结构如图9 所示。使用多通道温度记录设备对测试点进行测试。表4 为分别通过商业软件模拟、解析法和实验得到的结果。

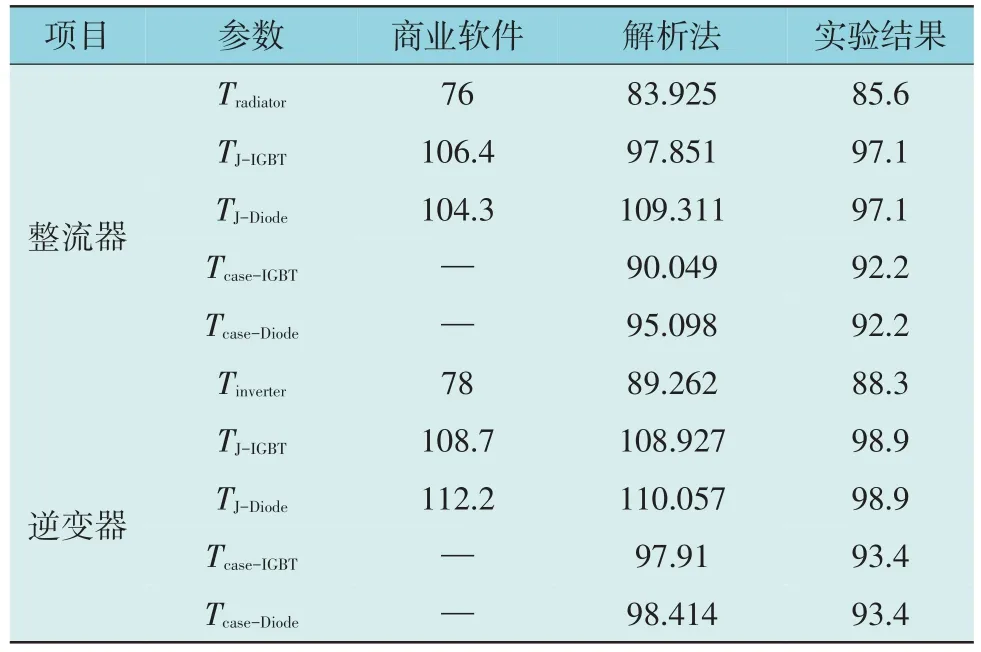
表4 商业软件仿真、解析法和实验测量结果的比较Table 4 Comparison results of commercial software simulation，analytical calculation and experimental measurement ℃

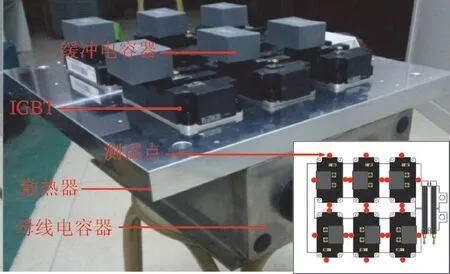
图9 调速系统主电路部分的三维结构Fig.9 Three-dimensional structure of speed control system main circuit

利用Solidworks 对散热器进行建模，同时采用workbench 进行固液耦合仿真，结果如图10 所示。将结果作为边界条件利用Steady-state Thermal 模块仿真，结果如图11。IGBT 底部和散热器接触位置最大温度为91.5 度，模块最大温度为108.6 度。图12为温升实验结果，可以看出仿真分析和实验结果比较符合，验证了本文所提损耗计算法的准确性。

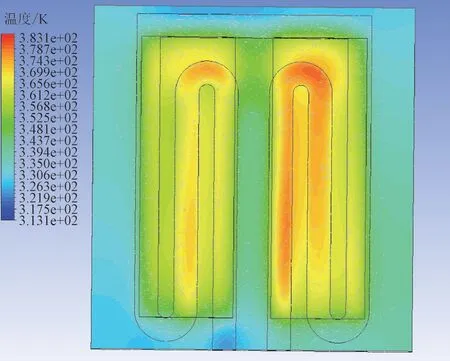
图10 Fluid Flow仿真结果Fig.10 Fluid Flow simulation result

图11 散热器温度分布Fig.11 Temperature distribution of radiator

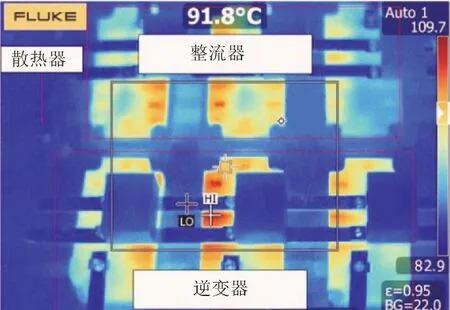
图12 温升试验Fig.12 Temperature rise test

如表4 所示，散热器温度的实测结果与所提出的解析法的结果吻合较好，而商业软件估算的温度值与实验结果存在一定的误差。与实验值吻合较好，验证了所提出解析法的正确性。

同时，所提出的解析法在过载情况下IGBT 的结温不超过额定值，满足系统要求。集电极电流、温度要求和逆变器选型合理。利用所提出的解析解的精确温度预测，变频调速系统中的功率器件可以采用3 300 V/200 A 级等级的IGBT。

6 结论

1）本文提出了一种基于栅极驱动电阻、直流母线电压以及环境温度和器件结温的解析法计算整流器及逆变器IGBT 的损耗和温度的方法。

2）提出了一种考虑电压、电流和器件结温的IGBT 模块选择方案。

3）采用的解析法损耗计算方案解决了商用软件中主电路拓扑和功率模块数据不完整、与实际不一致的问题。该计算方案能较好地反映结温、壳温和温升，与商用软件计算结果相比，在保证系统性能的前提下，能够减小水冷散热器的体积。