基于KL散度的配电网高阻抗故障检测研究

冯 楠，贺晋宏，魏 鑫，连 华，程树英，刘友波

（1.国网山西省电力公司，山西太原 030021；2.国网长治供电公司，山西长治 046011；3.福建网能科技开发有限责任公司，福建福州 350003；4.四川大学电气信息学院，四川成都 610000）

0 引言

为保障供电可靠性和企业收益，供电企业希望尽量减少短路故障引起的运行成本和停电时间[1]。研究有效的保护系统对于满足这些要求至关重要。其中，高阻抗故障（High-Impedance Fault，HIF）检测对配电网保护很重要。HIF 故障分为未破裂故障和破裂故障[2]。

HIF 主要与电弧现象有关，其主要特征是低电流、随机性、非线性和不对称性[3]。传统的过流保护装置不能快速、可靠地检测出故障电流。切换（投切）事件和非线性负载出现相似的结果，使得HIF检测更加困难。未检测到的HIF 可能会在馈线上持续很长时间，导致功率损失，由此产生的电弧可能引起火灾和触电[4]。

HIF 检测技术主要分为4 类：时域方法、频域方法、混合（时频）方法和启发式方法。时域方法基于时域电压/电流测量值实现。文献[5]采用电压测量值进行HIF 检测。当HIF 的故障电流低或HIF 位置到继电器的距离过大时，可能会降低由此产生的电压降，影响方法性能。文献[6]利用保护线路两端的电流测量值，基于差动保护原理检测HIF，但这种方法需要良好的通信基础设施和同步数据。文献[7]提出了基于数学形态学的HIF 检测工具，但是不能区分HIF 和非线性负载。文献[8]提出了一种利用基波和低次谐波附近的突发噪声信号进行HIF检测的方法，缺点是需要快速傅立叶变换（Fast Fourier Transform，FFT）和灵敏度低。同时，基于频域的技术在非线性负载下通常会出现误动作。在混合（时频）技术方面，文献[9]采用离散小波变换提取了HIF 特征。但是，这种方法计算量很大，且没有能力区分HIF 和非线性负载。启发式方法包括基于人工神经网络[10]、决策树[11]、支持向量机[12]、自适应神经模糊推理系统[13]和遗传算法[14]的方法。这种方法的主要缺点是处理训练数据集。

本文提出了一种基于电流波形的HIF 检测技术。HIF 特性导致前后半周期的电流波形不同。所提方法利用Kullback-Leibler（KL）散度量化了两个“半周期”电流之间的差异。首先阐述了研究所用的测试系统和HIF 检测的挑战，然后介绍了所提出的HIF 检测算法的原理，接着采用不同算例评估所提方法的性能，分析方法优越性。本文提出的HIF检测方法只需要测量变电站的电流，不需要对谐波分量进行任何变换和计算，可以将HIF 与非线性负载和切换事件区分开来，不仅具有较高灵敏度，而且不存在处理训练数据集的问题。

1 测试系统和HIF检测

1.1 测试系统

本文采用IEEE13 节点测试馈线作为研究测试对象，其工作电压为4.16 kV。图1 为该测试系统的单线图，变电站位于节点650，斜杠和黑色线表示电缆，2 个并联电容器组安装在节点611 和675 处，有1 个电压调节器和1 个在线变压器，线路有电缆和架空线。此系统馈线很短，负荷相对较高。此外，它还包括平衡和不平衡（单相和两相）负载。IEEE 13 节点测试馈线的参数见文献[15]。

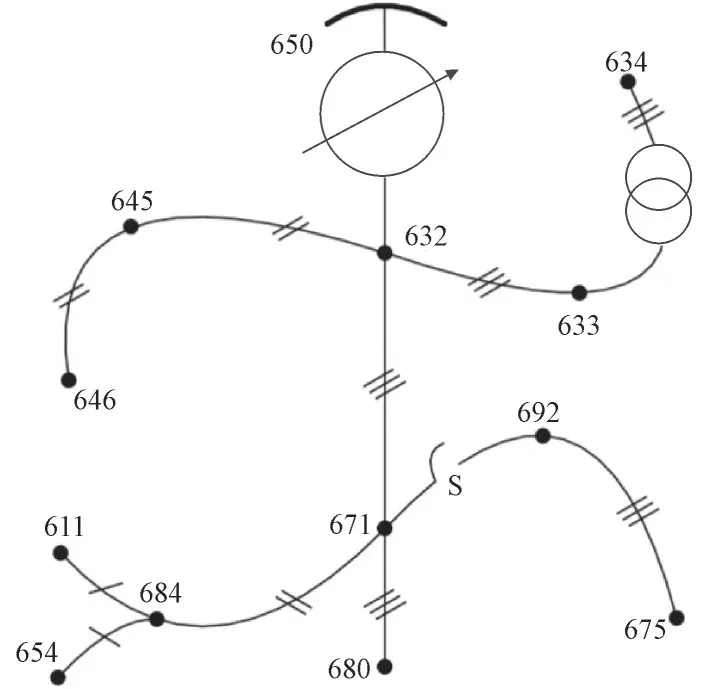
图1 IEEE13节点测试馈线单线图Fig.1 Single-line diagram of the IEEE 13 node test feeder

1.2 HIF建模

HIF 建模的精确性影响故障检测算法的高效性。HIF 的主要特征是与高阻抗表面接触产生的低故障电流、快速放电，地表漂浮导体产生的随机性，接触表面二氧化硅导致的不对称性，以及由各种电阻率引起的非线性[16]。文献[16]提出一种通过智能电表辅助配电网高阻抗故障检测的方法区分HIF与负荷、电容器、馈线和分布式能源投切事件、电压骤降和浪涌事件说明所提故障检测算法的有效性。在保证科学性前提下，采用了同一HIF 模型验证所提配电网高阻抗故障检测方法。图2 给出了HIF 模型[16]，包括两个二极管、两个可变直流电源和两个反并联可变电阻。

图2 HIF模型Fig.2 Model of HIF

图2 中Vp为模拟故障电流不对称的可变直流电源电压，Vn为模拟中间电弧熄灭可变直流电源电压，可变电阻Rp模拟故障电流不对称的电弧电阻，Rn为模拟中间电弧熄灭的电弧电阻，Vph为HIF 位置的相对地电压，Dp和Dn分别是等效二极管，Vn电流方向取决于馈线和直流电源电压的瞬时值。当Vph＞Vp时，故障电流流向地；当Vph＜Vn时，故障电流方向相反。如果Vn＜Vph＜Vp，则不存在故障电流。Vp和Vn的值大约设置为Vph的1/2 和1/4，随机变化为±10%，而Rp和Rn的值在200 Ω到300 Ω之间随机变化。

图3 给出了测试系统中单相接地故障的HIF模型电压和电流。HIF 的电压-电流特性如图4 所示。不对称的正负半周显示了HIF 的随机性，而灭弧导致电流波形在过零点附近中断。

图3 单相接地故障时HIF的电压电流波形Fig.3 HIF voltage and current waveforms

图4 HIF的电压-电流特性Fig.4 Voltage-current characteristic of HIF

1.3 HIF检测

现有的HIF 检测技术通常采用电压/电流测量实现[16]。图5 所示为变电站电压和电流波形。

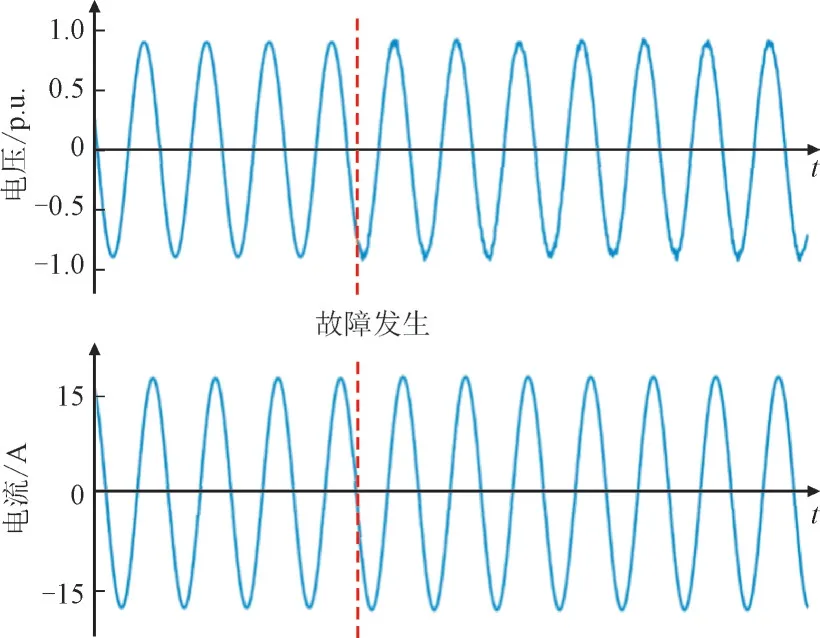
图5 HIF期间的电压电流波形Fig.5 Voltage and current waveforms during HIF

电压和电流幅值没有显著变化，这使得传统的保护继电器无法检测HIF。因此，现有的HIF 检测算法都试图揭示HIF 的独特特性。然而，负载和电容器组的切换会在波形中产生类似的特征，这使得HIF 检测有一定困难。另一方面，馈线连有非线性负载。与切换事件类似，非线性负载对波形的影响可能导致HIF 检测算法的误操作。因此，除了快速检测故障状态外，一个有效的HIF 检测方案应该能够将HIF 与切换事件和非线性负载区分开来。

2 HIF检测方法

2.1 HIF检测指标

由于HIF 故障电流低，传统的过电流继电器无法检测到HIF。需要对HIF 检测中的电压/电流波形进行分析。HIF 的非线性和不对称性使得每半周的电流波形与前半周不同。为了量化差异，提出使用KL（Kullback-Leibler，KL）散度相似性度量[17]。KL 散度又称相对熵，是信息论领域中著名的相似性度量，用于测量2 个概率分布之间的距离[18]。

首先，需要测量每相的电流。智能电子设备（Intelligent Electronic Device，IED）以4.8 kHz 对这些信号进行采样，每个周期的相位j处的电流测量矢量Mj为：

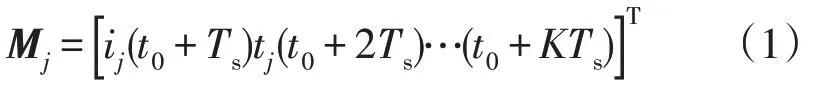
式中：t0为初始时刻；ij为相位j处的电流；Ts为采样周期；tj是相位j对应的时间；K为1 个周期内的样本数。

式中：M1,j为上半周期测量矢量；M2,j为下半周期测量矢量。

为了使正常工作条件下2 个后续半周期之间的差值为零，在式（3）中计算每个电流样本绝对值。2 个后续电流测量向量之间的KL 散度定义为：

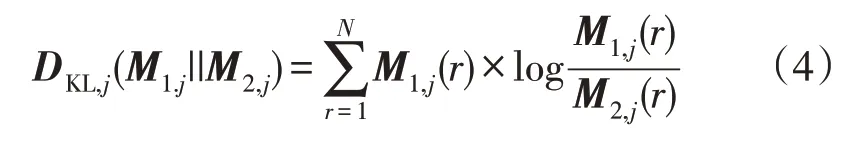
式中：N为半个周期的电流样本数；r为周期序号，即N=K/2。

当且仅当M1,j=M2,j时，KL 散度为零，DKL,j(M1.j||M2,j)为相位j处的KL 散度。

在正常运行期间，2 个随后半周期内的电流波形相似，因此，DKL,j=0。然而，当HIF 发生时，电流波形的非线性和不对称性使DKL改变。取a，b，c 三相DKL绝对值的最大值作为HIF 检测指标ξ（无量纲）：

当发生扰动时，有：

式中：ξth为干扰检测阈值。

2.2 HIF与切换事件的区别

切换事件也增加ξ，但其引起的失真只会持续几个周期，而HIF 会改变电流波形，直到它被清除。因此，另一个标准定义为：

式中:tξ为满足式（6）的持续时间；tw为等待时间。

由于非线性负载在每个半周期内产生相似的瞬态，ξ不会显著增加。因此，切换事件和非线性负载不会导致HIF 检测算法出错。

2.3 阈值选择

阈值的选取影响算法的性能。阈值小会降低该算法的精度，而阈值大会降低HIF 检测的速度。干扰检测阈值和等待时间计算如下：

式中：ξnormal和tw.normal为正常工作条件下HIF 检测指数的最大值，以及切换事件ξ＞ξth持续时间的最大值；SFξ和SFt为安全系数，用于保持所提方法的可靠性。

图6 给出了HIF 检测方案的流程图。

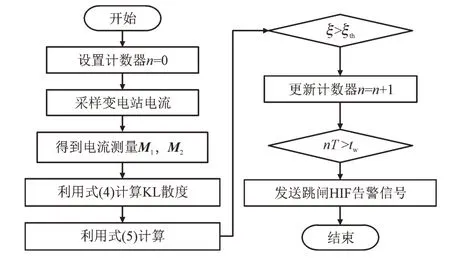
图6 HIF检测算法流程图Fig.6 Flowchart of proposed HIF detection algorithm

3 性能评估

采用Matlab/Simulink 对图2 中的HIF 模型进行仿真研究。变电站变压器中性点可靠接地。案例研究包括：HIF、平衡和不平衡负载切换、单相和三相电容器组切换、馈线供电、分布式能源（Distributed Energy Resource，DER）切换以及电压骤降和浪涌。ξnormal和tw.normal分别为2.5 和4 个周期，安全系数SFξ和SFt分别等于1.4 和1.5，干扰检测阈值（无量纲）和等待时间分别为3.5 和100 ms。

3.1 HIF的性能评估

为了评估所提HIF 检测算法的性能，在变电站附近（节点632）t=0.3 s 时模拟a 相的HIF。图7 给出了这种情况下的变电站电流和HIF 检测指数ξ（无量纲）。在故障开始前，M1，M2的第一和第二周期的电流波形是相同的，因此KL 散度DKL为零。当发生HIF 时，变电站电流无显著变化。然而，HIF的非对称性和非线性特性导致M1≠M2，DKL增加到90.38，超过了阈值。由于ξ＞ξth直到故障持续，该算法将该扰动正确地判定为HIF。

图7 632和652节点HIF期间变电站电流和HIF检测指标Fig.7 Substation current and HIF detection index duringHIF at nodes 632 and 652

为了验证所提HIF 检测指标的灵敏度，在节点652 处模拟a 相的HIF 作为距离测量点的远故障点。利用变电站电流计算出的HIF 检测指数如图8所示。ξ增加到4.25 并超过其阈值。ξ632，ξ652分别为节点632和652处的KL检测指标。在消除HIF之前，HIF 检测指标将保持在其阈值以上，此情况被验证为HIF。

3.2 负载切换

研究的第一个场景如下：具有最大负载的节点671 的三相负载在t=0.3 s 时接通。图8 给出了该场景的HIF 检测指标。ξ增加到5512，这是因为大负载切换的严重性远远大于HIF。在负载切换后的第一个周期内，M1≠M2；但是，在几个周期后，电流波形中的变化减小，并且在2 个半周期内对称，没有任何非线性特征。因此，ξ降低到其阈值以下。满足式（6）的持续时间为3 个周期，小于tw。因此，算法没有将这种情况归类为HIF。

在第二种情况下，针对非对称负载切换，评估了该算法的性能。为此，节点646 的两相负载（在相位b 和c 之间）在t=0.3 s 时断开，结果如图8 所示，HIF 检测指标增加到1193，ξ＞ξth的条件只满足3 个周期，tξ＜tw，可见所提算法不会错误诊断。ξ646，ξ671分别为节点646和671处的KL检测指标。

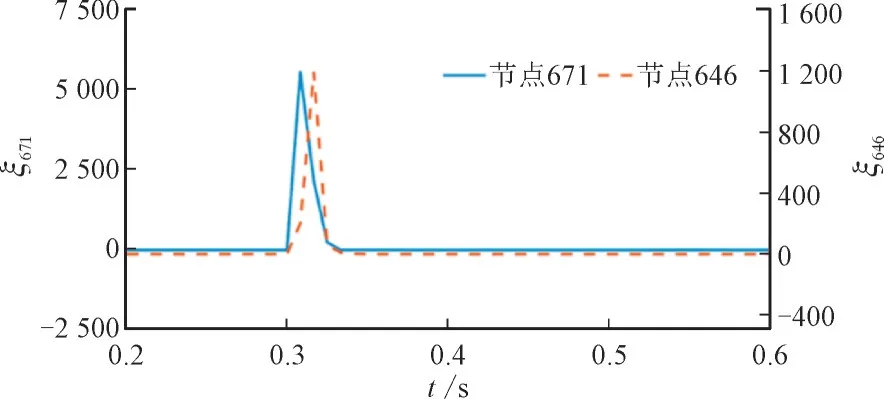
图8 在节点671处接入负荷和节点646处断开负荷的情况下所提HIF检测算法的性能Fig.8 Performance of proposed HIF detection algorithm during load energisation at node 671 and load deenergization at node 646

3.3 电容器投切

该案例研究证明了所提算法在电容器切换过程中的有效性。第一种情况是接通安装在节点671处的单相电容器，第二种情况是在t=0.3 s 时断开安装在节点646 处的三相电容器。图9 给出了仿真结果。ξ646，ξ671分别是节点646 和671 处的KL 检测指标。前者的HIF 检测指数增加到71.3，而后者增加到181.3。ξ在2 个周期后回到阈值以下，且式（7）不满足。因此，所提算法在电容器投切过程不会错误诊断。

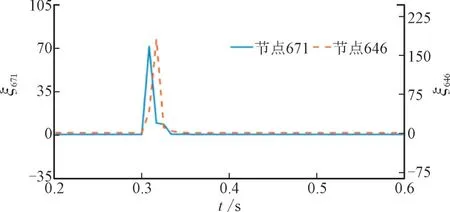
图9 节点611处电容器连通和节点675处电容器断开情况下所提HIF检测算法的性能Fig.9 Performance of proposed HIF detection algorithm during capacitor connection at node 611 and capacitor disconnection at node 675

3.4 馈线通电

开关S 在t=0.3 s 时闭合，以使节点692 和675通电。图10 给出了在这种情况下算法的性能。馈线通电导致ξ增加到1 234，这种瞬间跳跃的持续时间是3 个周期。因此，所提算法认定其为无HIF 情况。ξk，ξd分别是馈线切换和DER 的KL 检测指标。本节研究测试系统中存在DER 情况下所提算法的性能。为此，在t＝0.3 s 处将栅极连接的电耦合DER 单元连至节点634。HIF 检测指数增加到8.7，如图10 所示。然而，由于ξ在一个周期后返回到阈值以下，因此该算法不会对DER 切换产生误操作。

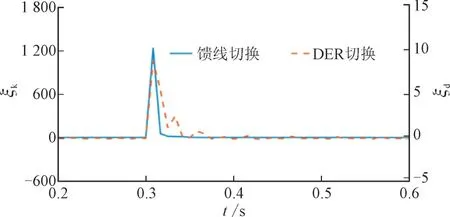
图10 配电馈线通电和DER切换过程中所提算法的性能Fig.10 Performance of proposed HIF detection algorithm for distribution feeder energisation and DER switching

3.5 电压骤降与浪涌

设定在0.3～0.375 s 之间发生电压骤降（额定电压的85%），然后在t=0.45 s 时出现电压浪涌（额定电压的110%），持续时间为0.075 s。图11 给出了此情况下的变电站电压波形和HIF 检测指标。当电压骤降发生时，ξ增加到1 686，当电压骤降被清除后，它再次跳到阈值以上。电压浪涌发生和间隙的ξ最大值分别为1 546 和1 210。然而，这些瞬间跳跃的持续时间小于3 个周期。因此，所提HIF 检测方法在电压骤降和电压浪涌时不会错误诊断。

图11 电压骤降和浪涌时变电站电压波形及HIF检测指标Fig.11 Substation voltage waveform and HIF detection index during voltage sag and swell

4 算例分析

4.1 不同接地方式对HIF检测的影响

本节评估所提HIF 算法在直接接地、阻抗接地、谐振接地和隔离接地四种接地方式的性能。为了模拟阻抗接地，变压器中性点通过4 Ω电阻接地。测试系统的等效电纳约为30 μs，模拟谐振接地所需的中性点与接地之间的感应电抗约为10 kΩ。为了实现高阻抗，消弧线圈与中性点接地变压器一起使用。模拟结果如图12 所示。实验结果验证了算法在不同接地方式下的有效性。

图12 不同接地方式下所提算法的性能Fig.12 Performance of proposed algorithm under various grounding modes

4.2 算法可扩展性研究

为了验证所提HIF 检测算法的可扩展性，本节采用IEEE 34 节点测试馈线。图13 给出测试馈线的单线图，是一条具有轻负载的长馈线。变电站位于节点800 处。IEEE 34 节点测试馈线的工作电压为24.9 kV。在第一个场景中，HIF 在节点816（相位a）处，第二个场景是在节点844 处连接三相电容器，第三个场景在节点810 处断开单相负载（相位b）。所有事件发生在t=0.3 s 时，仿真结果如图14 所示。虽然HIF 检测指标在所有模拟条件下都有所增加，但在切换事件3 个周期后仍保持在HIF 条件下的阈值以上，验证了该算法对各种测试馈线的有效性。

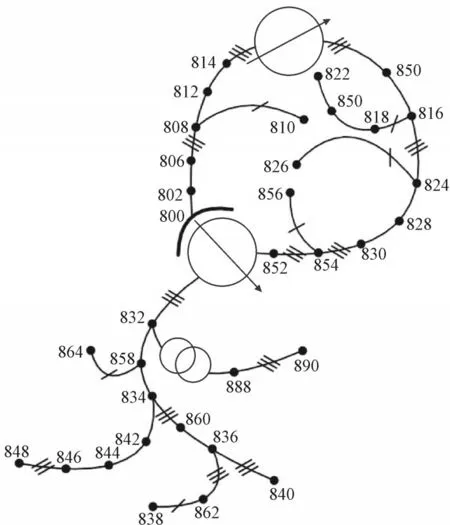
图13 IEEE 34节点试验馈线单线图Fig.13 Single-line diagram of IEEE 34 node test feeder

图14 IEEE 34节点测试馈线HIF检测算法的性能Fig.14 Performance of proposed HIF detection algorithm for IEEE 34 node test feeder

4.3 比较评估

4.3.1 与现有算法的比较

本节比较所提出算法与基于谐波、小波和MM的HIF 检测方案的有效性。采用IEEE 13 节点测试馈线作为测试对象。在非线性负载和HIF 存在的情况下，研究了每种算法的性能。非线性负载是一个650 kW，3.6 kV 的直流负载，该负载使用六脉冲转换器电桥连接到节点632。t=0.3 s，模拟的HIF发生在节点632（a 相）。文献[19]提出的基于谐波的HIF 检测算法指出，在HIF 过程中，3 次谐波电流大于5 次谐波电流。图15 给出了HIF 期间存在非线性负载时的变电站电流波形及其3 次和5 次谐波分量。非线性负载的存在导致3 次谐波（2.8 A）低于第5 次谐波电流（30.8 A），导致检测HIF 失败。

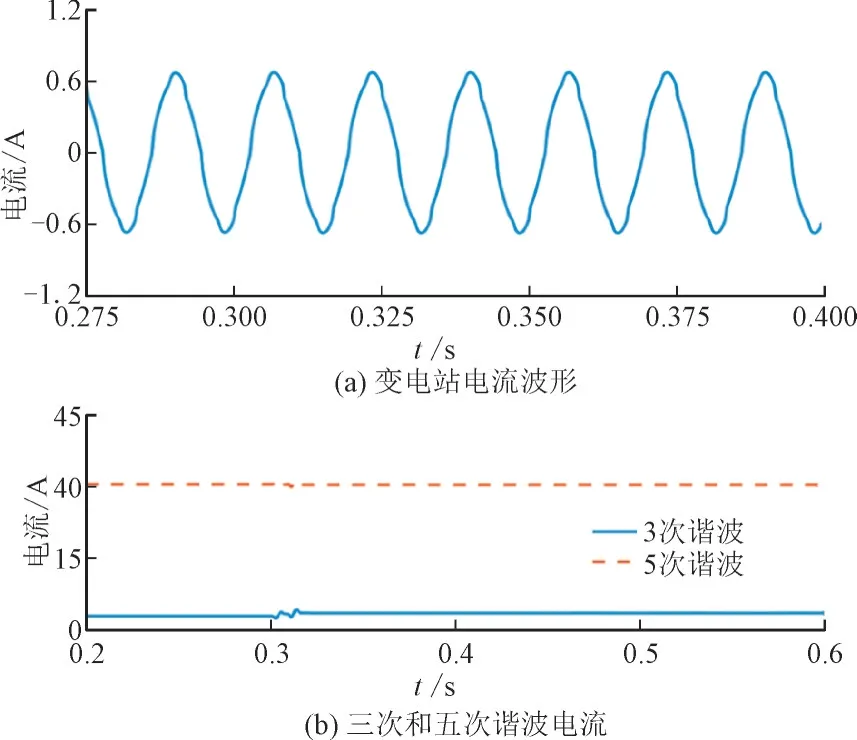
图15 基于谐波的HIF检测算法的性能Fig.15 Performance of harmonic-based HIF detection algorithms

文献[20]中提出的算法通过计算小波系数能量（wavelet coefficient energy，WCE）来检测由HIF 引起的瞬态变化，ζ为其检测指标，无量纲。而文献[21]中提出的方法使用MM（Multi-Model，MM）技术通过开闭差分运算（Close-open Difference Operation，CODO）来检测HIF。τ是其检测指数，无量纲。为了评估这些方法的性能，本文研究了非线性负载切换和HIF 2 种情况。2 种情况均发生在t=0.3 s 时，仿真结果如图16 所示。这些方法在非线性负载切换时不能正常工作。

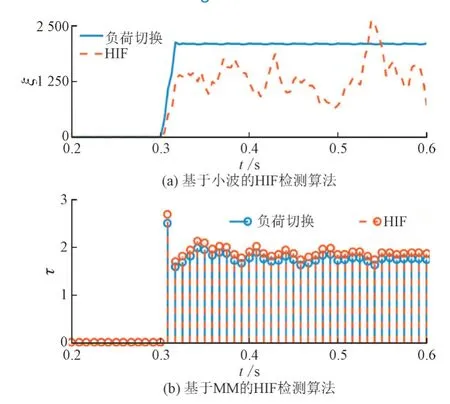
图16 HIF和非线性负载切换的HIF检测算法性能Fig.16 Performance of HIF detection algorithms during non-linear load switching and HIF

图17 给出了所提算法在有非线性负载情况下的性能。

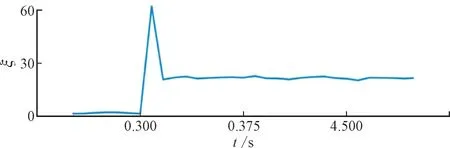
图17 非线性负载下HIF检测算法的性能分析Fig.17 Performance of proposed HIF detection algorithm under non-linear load

在t=0.3 s 发生HIF 前，所提出的HIF 检测指标接近于零，验证了非线性负载的存在不会导致所提算法出错。当HIF 发生时，ξ跳变并保持在阈值以上；因此，根据所提算法，这种情况被归类为HIF[22-25]。

4.3.2 相似性测度的比较

本文采用KL 散度相似性度量作为HIF 检测指标，将其与相关系数、余弦相似性和Jaccard 系数[17]3 种相似性度量进行比较。在t=0.3 s 时，在节点671（相位a）出现HIF，用不同相似性度量来计算式（5）的HIF 检测指数。图18 给出了仿真结果。由图18 可见，相关系数、余弦相似性和Jaccard 系数的值很小。由于降低HIF 检测阈值可能会导致干扰跳闸，这些很小的值可能无法检测到。然而，基于KL 散度的HIF 检测指标达到了15.8，即远高于ξth的HIF 检测阈值，验证了该方法的有效性。

图18 不同相似性度量在检测HIF时的灵敏度比较Fig.18 Comparison between the sensitivities of various similarity measures in detecting HIF

5 结论

本文提出了一种时域方法来解决HIF 检测问题。该方法将电流波形的每个周期分为2 个半周期，并用KL 散度来量化它们的差异性。在正常工作条件下，该测量值为零；HIF 的非线性和不对称特性会改变KL 散度，使其成为有效的HIF 检测指标。该方法不需要计算谐波分量和训练数据集就能够检测出HIF。为了区分HIF 和切换事件，计算保持所提指标超过阈值的持续时间。所提方法在切换负载、电容器、DER、馈线通电、电压骤降和浪涌方面均无误动作。通过与现有的HIF 检测方案的比较，证明了该算法在非线性负载下的优越性。通过在IEEE13 节点和IEEE34 节点测试馈线上进行的多个HIF 和无故障场景测试，验证了所提HIF 检测算法的有效性。