高等几何背景下的解析几何试题探究

⦿北京市第四十三中学 柏任俊

⦿北京市育才学校 贾春花

⦿湖北大学数学与统计学学院 毛 井

1 引言

高等几何背景下的解析几何问题一直是高考命题的热点，例如2020年北京卷第20题，既有高等几何的背景，又重点考查了先猜后证、化归与转化的数学思想，是一道非常难得的优秀题目．下面笔者对这道题目进行深入探究．

2 试题呈现

(Ⅰ)求椭圆C的方程；

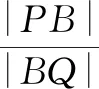
3 分析与思考

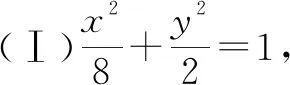
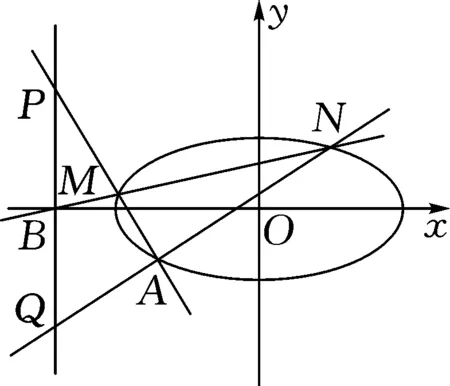
图1

(4k2+1)x2+32k2x+(64k2-8)=0.

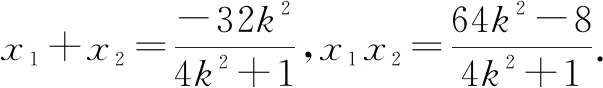
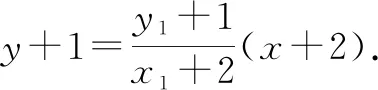
令x=-4，可得

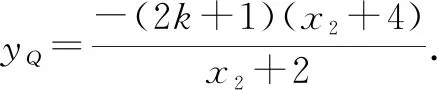
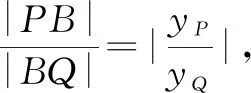
又(x1+4)(x2+2)+(x2+4)(x1+2)

=2[x1x2+3(x1+x2)+8]

=0.

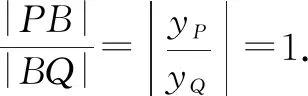
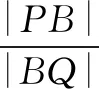
很多学生不难得到以上结论，但是再往下学生该怎么做呢？在这里，先猜后证的研究方法就显得尤为重要了．

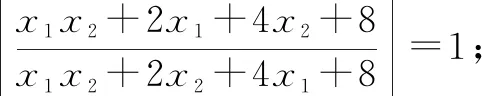
第二步，他还要知道要证明

成立，就只需证明

(x1x2+2x1+4x2+8)+(x1x2+2x2+4x1+8)

=2x1x2+6(x1+x2)+16=0

成立．即证x1x2+3(x1+x2)+8=0成立.此后的问题就非常容易了．

由此可见，高考数学北京卷解析几何题的落脚点还是在“能力”上.就此题而言，考查学生“先猜后证”的研究方法和数学运算的基本素养，这是非常重要的．

4 背景分析

本题的选题来源于高等几何中的极点极线理论，当然它不是高中数学课程标准中的学习内容，也不在高考考查的范围内，但由于该理论体现了圆锥曲线的基本性质，经常会成为命制解析几何试题的背景．如果中学教师能够了解该理论，熟悉有关性质，那么我们就能够站在比较高的观点下去看待这些试题，就能够“看透”试题中蕴含的有关极点极线的知识背景.下面给出高等几何中有关二次曲线的极点极线的概念及相关理论．

4.1 极点与极线的几何定义与性质

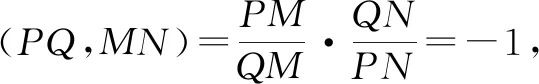
定义1[2]不在二次曲线Γ上的点P关于一条二次曲线的调和共轭点的轨迹是一条直线，这条直线叫做点P关于此二次曲线Γ的极线，点P称为这条直线关于此Γ的极点．一般我们把这个定义称为极点极线的几何定义．

图2

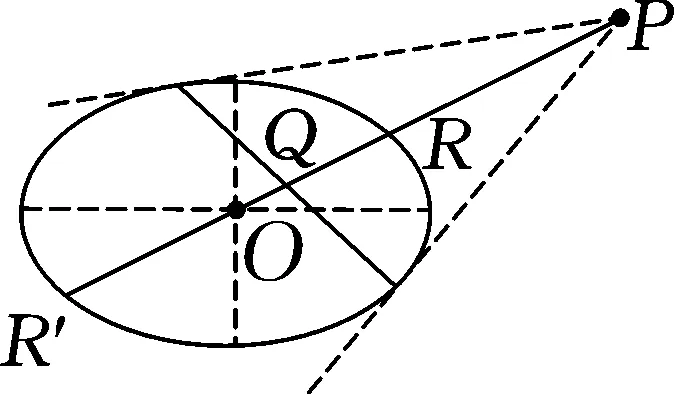
图3

推论2[2]如图3，设点P关于有心圆锥曲线G的调和共轭点为点Q，PQ连线经过圆锥曲线的中心O，且与G交于两点R,R′，则有OR2=OP·OQ.反之若有此式成立，则点P与Q关于G调和共轭．

4.2 极点与极线的代数定义

定义2[3]已知圆锥曲线Γ:Ax2+Cy2+2Dx+2Ey+F=0(A2+C2≠0)，则称点P(x0,y0)和直线l:Ax0x+Cy0y+D(x+x0)+E(y+y0)+F=0是圆锥曲线Γ的一对极点和极线，一般我们把这个定义称为极点极线的代数定义．

5 高等几何背景下的解法探究

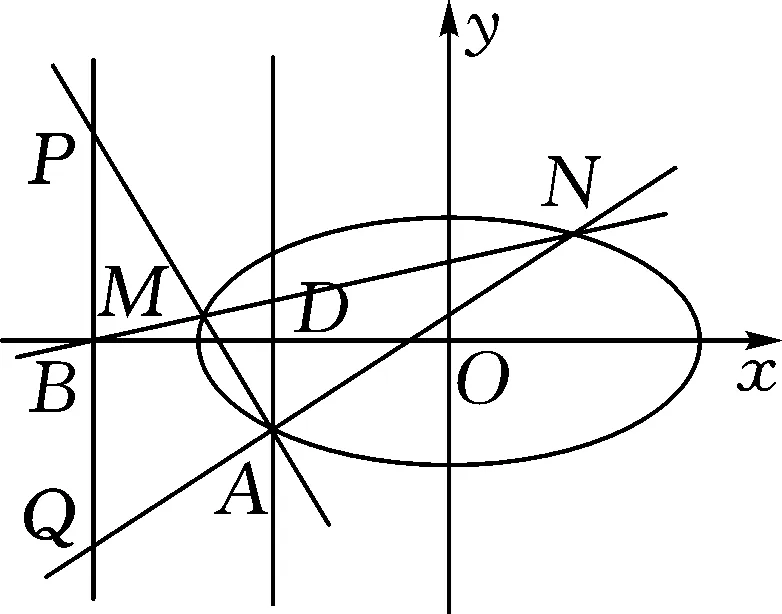
图4

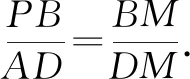
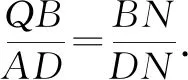
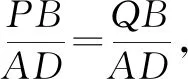
继续探究这道题，点A(-2,-1)与B(-4,0)有没有关联呢？A,B两点满足什么关系结论成立呢？有没有更一般的结论呢？我想这些都是值得我们去研究的．

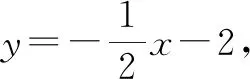
那我们可以大胆地猜想，如果保持点B固定，切线AB进化为割线，直线MF,NE分别交直线x=-4于点P,Q，|PB|=|BQ|还成立吗？

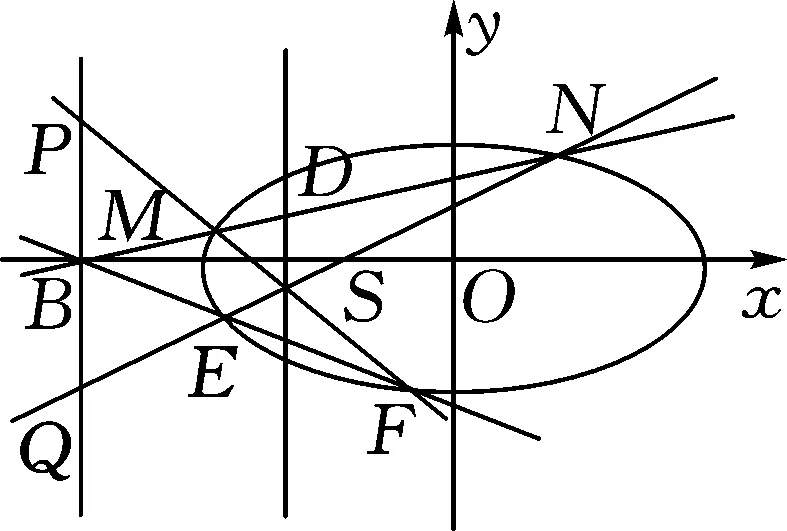
图5

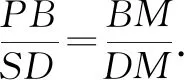
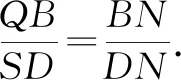
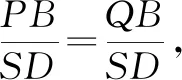
其实从证明的过程可以看出，如果点B是x轴上任意一点(t,0)，上述结论也成立．于是从这道高考题中得到下面的推广结论：

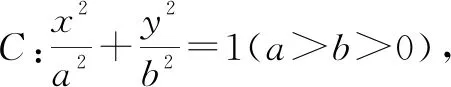
当然这个一般结论让学生做的话，计算量会非常大，所以可以把题目难度降低，这道北京高考题就是上述结论的一个简单特殊情形．我们可以把上面结论中过点B的一条割线BEF设定为x轴，这样E(-a,0),F(a,0)为椭圆的两个顶点，这个问题的计算量就小了很多，也非常适合学生来做．

6 其他考题的相同几何背景

以高等几何中的极点极线为背景的解析几何题目非常多，2020年全国1卷理科压轴题就是其中一个．

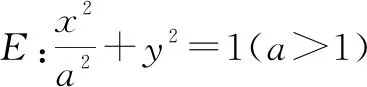
(1)求E的方程；(2)证明：直线CD过定点．

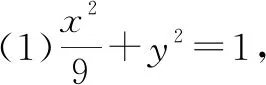
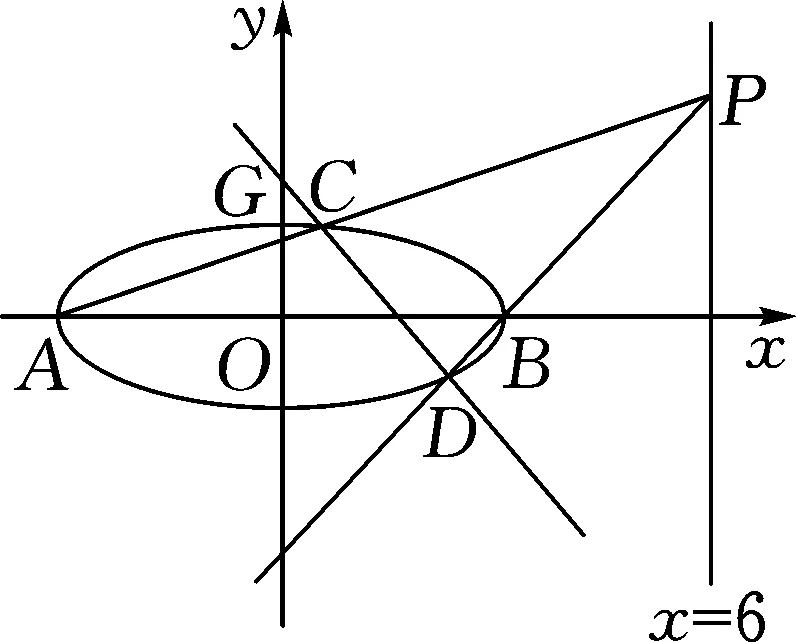
图6

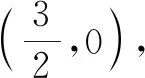
7 结束语

高等几何下的极点极线理论蕴含着非常丰富的内容，它是解析几何命题的内在背景．作为中学一线教师，掌握一些极点极线理论，从高等几何的角度去研究高中解析几何题目，有助于我们深层次地理解高等几何与初等几何之间的内在联系．