回热型S-CO2布雷顿循环的效率分析与优化

夏少军 金晴龙 吴志祥

(海军工程大学 动力工程学院,湖北 武汉 430033)

现代燃气轮机由于启动快、体积小、功率密度高等优点而被广泛应用于舰艇和船舶领域，但燃气轮机的排烟温度较高，若直接排放到环境中将导致大量的余热资源浪费。为了提高能源利用效率，有必要加强对燃气轮机烟气余热的回收利用[1- 4]。超临界二氧化碳(Supercritical Carbon Dioxide，S-CO2)由于其化学性质稳定、流体流动性好、传热效果好等优良特性，可在接近室温的条件下达到超临界状态，是理想的热力循环工质。以S-CO2为工质的布雷顿动力循环在船舶余热回收利用领域具有光明、广阔的应用前景[5- 8]。

应用经典热力学理论，诸多学者对S-CO2布雷顿循环展开了研究。王喜军等[9]提出一种由S-CO2布雷顿循环和有机闪蒸循环组成的新型联合循环，研究了压比、蒸发器蒸发温度对效率的影响。Deng等[10]以再压缩S-CO2布雷顿循环为研究对象，研究了不同透平进口温度下循环压比对效率的影响。Wu等[11]提出一种回热型S-CO2布雷顿循环和氨水吸收式制冷循环组成的新型联合冷却和动力系统，研究了关键参数(包括压缩机出口压力、透平入口温度等)对循环性能的影响，并采用NSGA-Ⅱ算法对其进行了多目标优化。

上述工作采用经典热力学理论研究了不同类型的S-CO2布雷顿循环性能，但均未详细考虑实际工程循环中工质与热源间有限温差传热等不可逆性因素对循环性能的影响。有限时间热力学[12- 14]是现代热力学理论的一个重要分支，它实现了热力学、传热学、流体力学和化学反应动力学等多个基础学科理论的交叉融合，着重研究在“有限时间”或“有限尺寸”约束下的各类过程、循环和装置的最优性能或最优构型[15- 18]。陈林根等[19- 21]将有限时间热力学与热经济学相结合，提出了有限时间经济分析法，在以理想气体为工质的布雷顿循环研究中取得了大量研究成果。杨博等[22- 23]分别以恒温热源闭式内可逆回热布雷顿热电冷联产装置和不可逆中冷回热布雷顿热电联产装置为研究对象，分析了回热器热导率、热电比等设计参数对输出率和效率的影响。王俊华等[24]以高炉余能余热驱动内可逆中冷回热Brayton热电联产循环为研究对象，分析了总压比、中间压比等设计参数对性能的影响。陈林根等[25]研究了回热器热导率、循环压比等设计参数对高炉余能余热驱动的闭式回热布雷顿循环热电冷联产装置性能的影响。齐伟等[26]以等温加热修正的双布雷顿循环为研究对象，分析了底循环压比和换热器有效度等参数对系统输出率和效率的影响。而在S-CO2布雷顿循环的有限时间热力学研究中，Na等[27]针对预热型S-CO2布雷顿循环回收LM-2500PE型和G4型燃气轮机的余热，分析了透平进口温度、工质质量流率和透平进口压力对循环效率和输出功率的影响。

文中应用有限时间热力学理论，建立考虑热源与循环工质间以及回热器中高低温工质间有限温差传热、不可逆压缩、不可逆膨胀等不可逆性的回热型S-CO2动力循环模型，首先对循环性能进行分析，然后在总热导率一定的约束下，以效率最大为目标，对循环压比、工质质量流率以及各个换热器的热导率分配比进行优化。

1 回热型S-CO2布雷顿循环的物理模型

回热型S-CO2布雷顿循环装置的流程图和T-s图(T为温度，s为比熵)分别如图1和图2所示。回热型超临界S-CO2布雷顿循环装置主要由压缩机、回热器、加热器、透平、冷却器等设备组成。图2中，过程1—2s为压缩机中的理想可逆绝热压缩过程，过程1—2为压缩机中的实际不可逆绝热压缩过程[26,28]，2—3为回热器中的吸热过程，3—4为从高温热源的吸热过程[26,28]，4—5为透平中的实际不可逆绝热膨胀过程，4—5s为透平中的理想可逆绝热膨胀过程，5—6为回热器的放热过程，6—1为向低温热源的放热过程[26,28]。

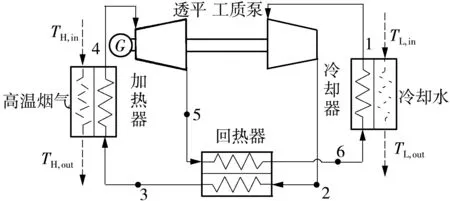
图1 回热型S-CO2布雷顿循环的流程Fig.1 Flow chart of recuperative S-CO2 Brayton cycle

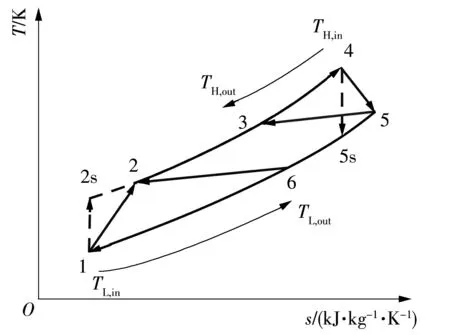
图2 回热型S-CO2布雷顿循环的T-s图Fig.2 T-s diagram of recuperative S-CO2 Brayton cycle

压缩机和透平的效率用ηc和ηt来表示：

ηc=(h2s-h1)/(h2-h1)

(1)

ηt=(h4-h5)/(h4-h5s)

(2)

式中，h1为进入压缩机前S-CO2的比焓，h2s为经过可逆绝热压缩过程后S-CO2的比焓，h2为不可逆压缩过程后S-CO2的比焓,h4为进入透平前S-CO2的比焓，h5s为经过可逆绝热膨胀过程后S-CO2的比焓，h5为不可逆膨胀过程后S-CO2的比焓。

设TH,in和TH,out分别为高温烟气的进口温度和出口温度，K；TL,in和TL,out分别为冷却水的进口温度和出口温度，K；mH、mL和mwf分别为热源、冷源和工质的质量流率，kg/s；cp,L和cp,H分别为冷、热流体的比定压热容，kJ/(kg·K)。根据文献[26,28]，定义热导率为换热器传热面积与总传热系数之积，表征换热器换热能力的强弱，加热器、冷却器和回热器的热导率分别用UH、UL和UR表示。考虑到加热器、冷却器和回热器均为逆流式换热器，根据工质与热源间的换热和热源性质可得吸热率QH、放热率QL、回热率QR分别为[26,28]

cp,HmH(TH,in-TH,out)

(3)

cp,LmL(TL,out-TL,in)

(4)

(5)

由工质的热力性质得QH、QL和QR分别为

QH=mwf(h4-h3)

(6)

QL=mwf(h6-h1)

(7)

QR=mwf(h3-h2)=mwf(h5-h6)

(8)

式中，h3为经过回热器预热后S-CO2的比焓，h6为经过回热器预冷后S-CO2的比焓。

定义循环的总热导率UT为各个换热器热导率之和：

UH+UR+UL=UT

(9)

总热导率与循环装置中加热器、冷却器和回热器所采用的材料、几何结构以及工作流体的热物理性质等因素有关，在工程上代表了循环装置建造的初始投资成本。在实际工程应用中，受限于应用环境空间和装置建造成本，循环装置的尺寸并不具备无限放大的可能，因此换热器的总热导率是有限的。文中考虑这一约束，假设总热导率为定值。由上述分析可知，虽然热导率是与热量、温度等参数相关联的，但与热量、温度等参数相比，热导率与装置初始投资成本直接关联，且直接反映了对应的换热器换热能力的强弱，因此以热导率为变量的优化结果在工程上更为清晰直观，同时一旦各换热器热导率确定，则循环的相应状态点温度和过程热量也可确定，所以，文中采用热导率来表征模型。定义热导率分配比Ψ为各个换热器热导率与总热导率之比，用以表征各换热器热导率在总热导率中的占比，则回热器热导率与循环装置总热导率之比ΨR=UR/UT，加热器热导率与循环装置总热导率之比ΨH=UH/UT，冷却器热导率与循环装置的总热导率之比ΨL=UL/UT，并存在如下关系：

ΨH+ΨL+ΨR=1

(10)

对于回热型S-CO2布雷顿循环，其循环净功率Wnet定义为透平功率与压缩机功率之差：

Wnet=mwf(h4-h5)-mwf(h2-h1)

(11)

eH=cp,HmH[(TH,in-TH,out)-T0ln(TH,in/TH,out)]-

cp,LmL[(TL,out-TL,in)-T0ln(TL,out/TL,in)]

(12)

式中，T0为环境温度。

在实际工程领域，单纯以输出功率最大为目标来评价各种形态的能量相互转换过程具有一定的局限性，作为评价能量“量”和“质”的参数，无法通过通常的能量平衡计算和能量转换效率反映出其利用程度，而通过计算效率可以更好地反映能量利用的合理性。对于整个循环，循环效率ηex定义为输出与输入之比，其中输出为循环的净输出功率Wnet，而输入为循环净输入的热量eH。效率定义式为

ηex=Wnet/eH

(13)

文中采用Matlab软件编写了回热型S-CO2循环的有限时间热力学分析与优化程序。对于循环性能分析，通过给定的边界条件(TH,in、TL,in、UH、UL、UR、ηt、ηc)，应用fsolve函数可求解各个状态点的温度与比焓，分析不同工质质量流率、压缩机、透平内效率以及总热导率下该循环效率与压比之间的关系。对于循环性能优化，以式(13)中效率ηex最大为优化目标，在ΨH+ΨL+ΨR=1(总热导率UT为定值)约束下，以压比、质量流率mwf和3个换热器的热导率分配比ΨH、ΨL、ΨR为决策变量，按以下3个步骤进行优化：①在给定的压比与工质质量流率下求效率ηex最大时ΨH、ΨL、ΨR之间的最优分配；②进一步释放压比，在压比3～7的范围内求最大效率ηex,max所对应的压比以及各个换热器热导率分配比；③释放工质质量流率，求解不同工质质量流率下ηex,max随工质质量流率的变化关系，以及ηex,max所对应的工质质量流率、压比以及各个换热器的热导率分配比，具体循环性能优化计算流程如图3所示。S-CO2的热力学物性采用 REFPROP 物性库进行查询，该物性库中嵌入了专门为CO2所建立的Span-Wang EOS模型，在超临界区域具有非常高的预测精度。

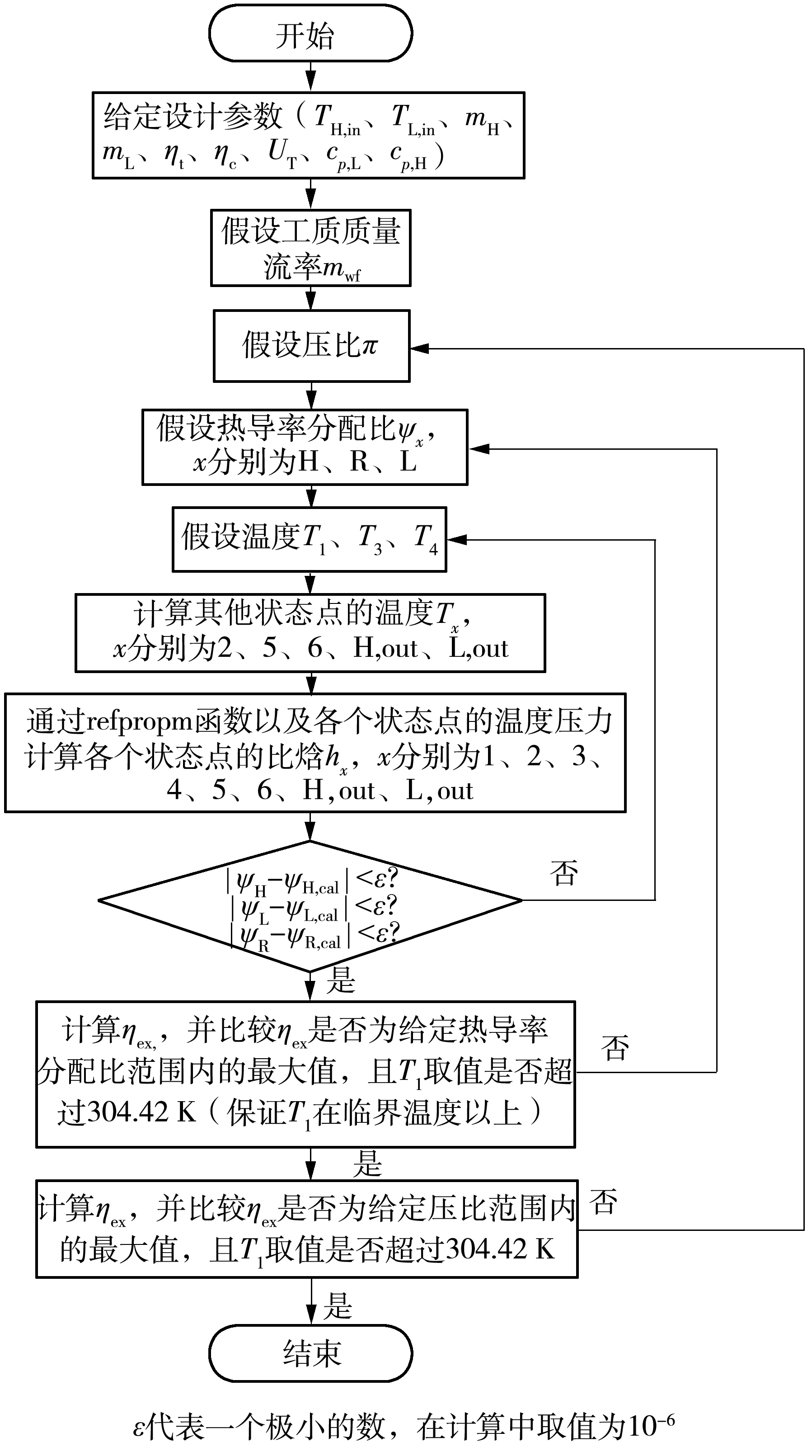
图3 循环性能优化计算流程图Fig.3 Calculation flow chart of cycle performance optimization

2 数值算例与讨论

2.1 模型验证

文献[11]应用经典热力学和能量系统技术经济学理论对高温烟气驱动的回热型S-CO2布雷顿循环与氨水吸收式制冷机联合装置进行了分析与优化。回热型S-CO2布雷顿循环热效率定义为循环净功率与从高温烟气中的吸热量之比，即热力学第一定律效率。文中在与文献[11]中回热型S-CO2布雷顿循环工质各状态点温度、压缩机和透平内效率等参数均相同的条件下，经计算得到的热效率与文献[11]所得的热效率数值相差0.053%，这验证了文中循环参数计算方法的正确性。文献[11]中的计算模型是基于经典热力学理论构建的回热型S-CO2布雷顿循环模型，主要考虑联合装置的整体投资、运行、收益和维护费用，从技术经济角度对联合装置进行了分析与优化，未考虑S-CO2布雷顿循环内部加热器、冷却器和回热器间的热导率最优匹配。文中模型较为详细地考虑了热源与工质间有限温差传热的不可逆性，更为贴合工程实际，同时从纯热力学角度对S-CO2布雷顿循环效率性能进行分析，并以效率最大为目标，对循环内部加热器、冷却器和回热器间的热导率最优匹配进行了优化，是对文献[11]研究内容的进一步拓展与深化。

文献[29]应用计算流体动力学(CFD)软件对回热型S-CO2布雷顿循环中的涡轮机循环参数进行了优化设计，相比于文献[11]，文献[29]中的循环数据是基于成熟的GateCycle软件进行模拟的[30]，同时透平参数部分有实验数据的支撑，更加真实可靠。为了更好地验证文中模型的准确性，本研究进一步以文献[29]中的循环数据为参照，运用Matlab软件仿真计算，并与文献[29]中的结果进行比较，其中η代表热效率，为净功率与吸热量之积，ηex=Wnet/QH。表1给出了模型验证计算选取的参数初值，除热导率UH、UR和UL的取值为文中设定之外，其他参数的取值均与文献[29]中相同。表2给出了文献[29]和文中计算的回热型S-CO2布雷顿循环各状态点温度、循环热效率和循环净功率的比较结果。由表2可知，应用文中模型计算出来的循环状态点温度与文

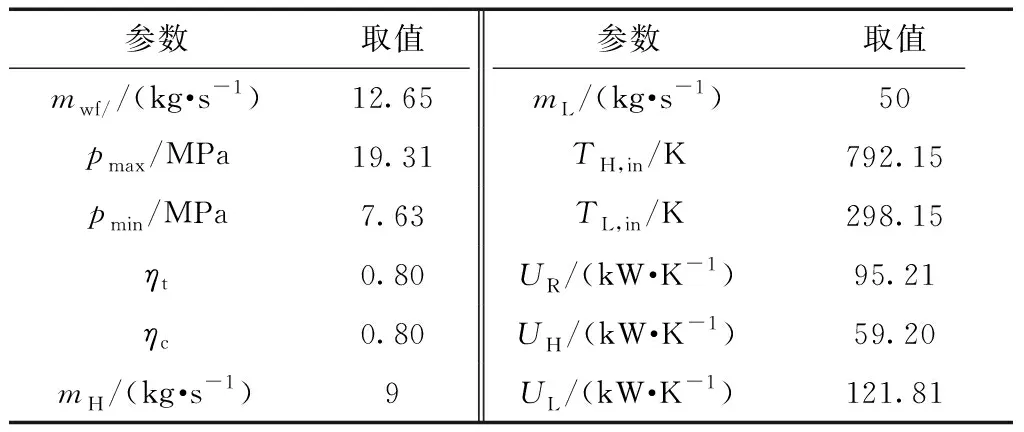
表1 模型验证计算选取的参数初值Table 1 Initial parameter values for model verification calculation

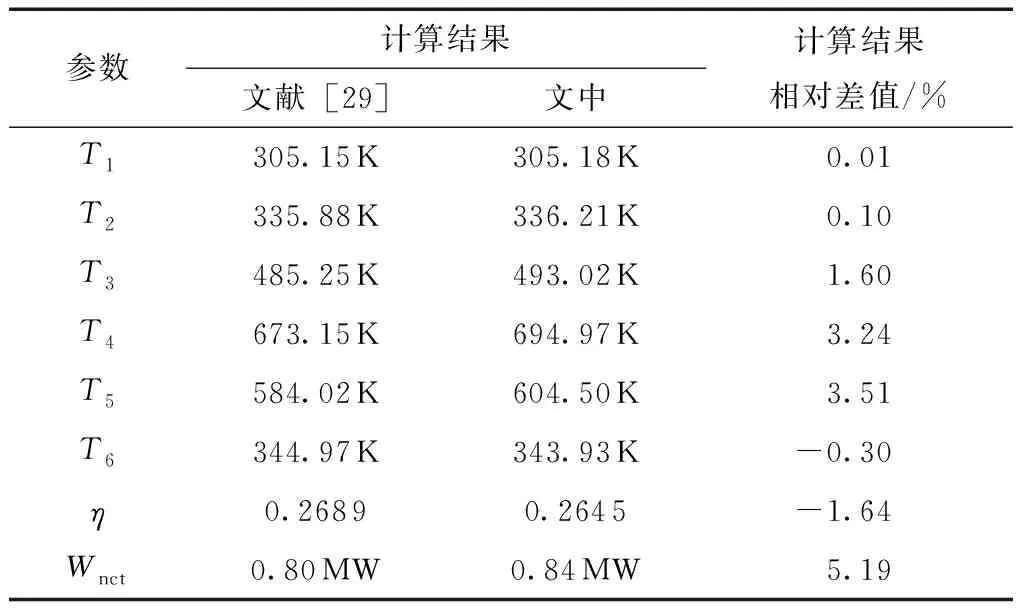
表2 模型验证计算结果比较Table 2 Comparison of calculation results for model validation

献[29]中结果的误差最高为3.51%，热效率误差为-1.64%，循环净功率误差为5.19%。可见，除循环净功率误差相差略大之外，主要状态参数和性能参数的计算结果与文献[29]结果均比较吻合。计算误差的产生主要是因为文献[29]中额外考虑了换热器以及流动过程中压降的影响，而文中模拟计算暂未考虑部件内部压降的影响。上述参数计算结果及分析充分说明，文中模型具有良好的可靠性。

2.2 循环性能分析

根据文献[27]，设定热源为高温烟气(其组分的质量分配占比分别为：N2，78.12%；O2，20.96%；Ar，0.92%)，冷源为冷水，其中热源和冷源的比定压热容由Matlab调用REFPROP计算获得，具体的初始设计参数如表3所示。

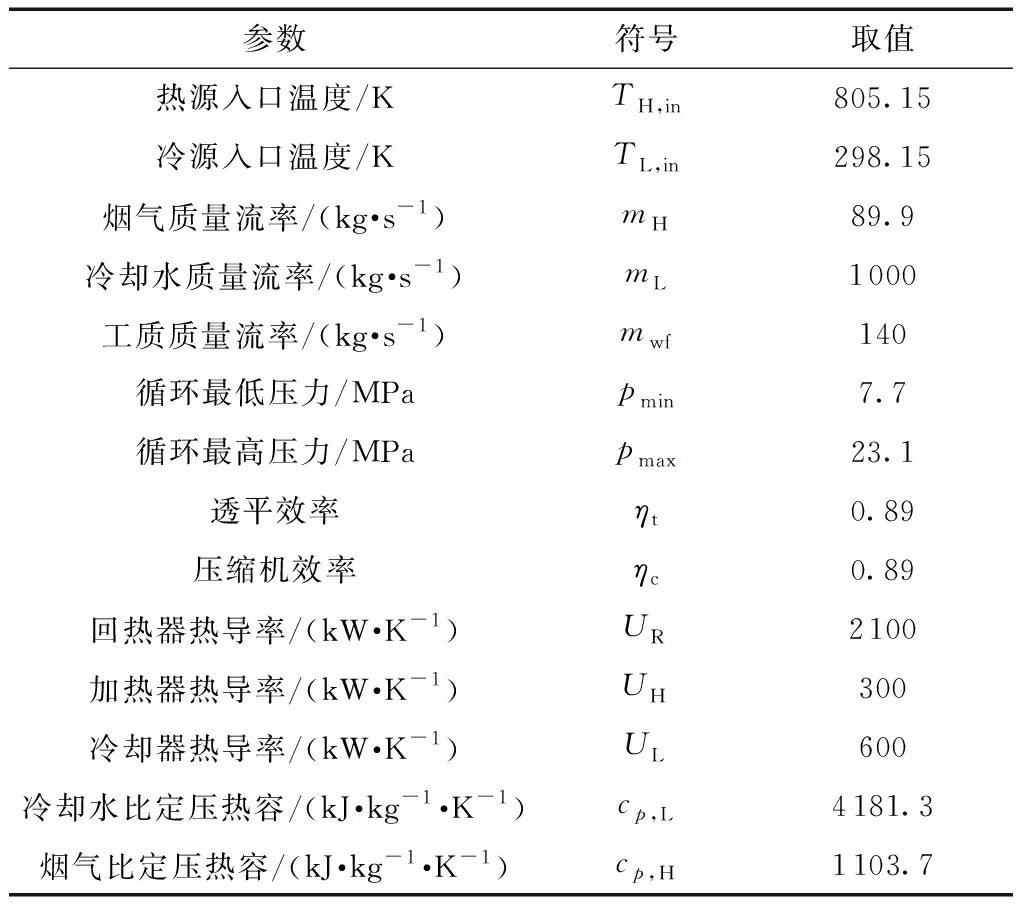
表3 初始设计参数Table 3 Initial design parameters

为了分析工质质量流率mwf、压缩机效率ηc、透平效率ηt、总热导率UT对循环效率ηex及相应的最佳压比maxη的影响规律，统一以压比为横坐标、效率ηex为纵坐标作图，并分别分析mwf、ηc、ηt、UT等参数变化对ηex-特性曲线的影响。

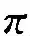
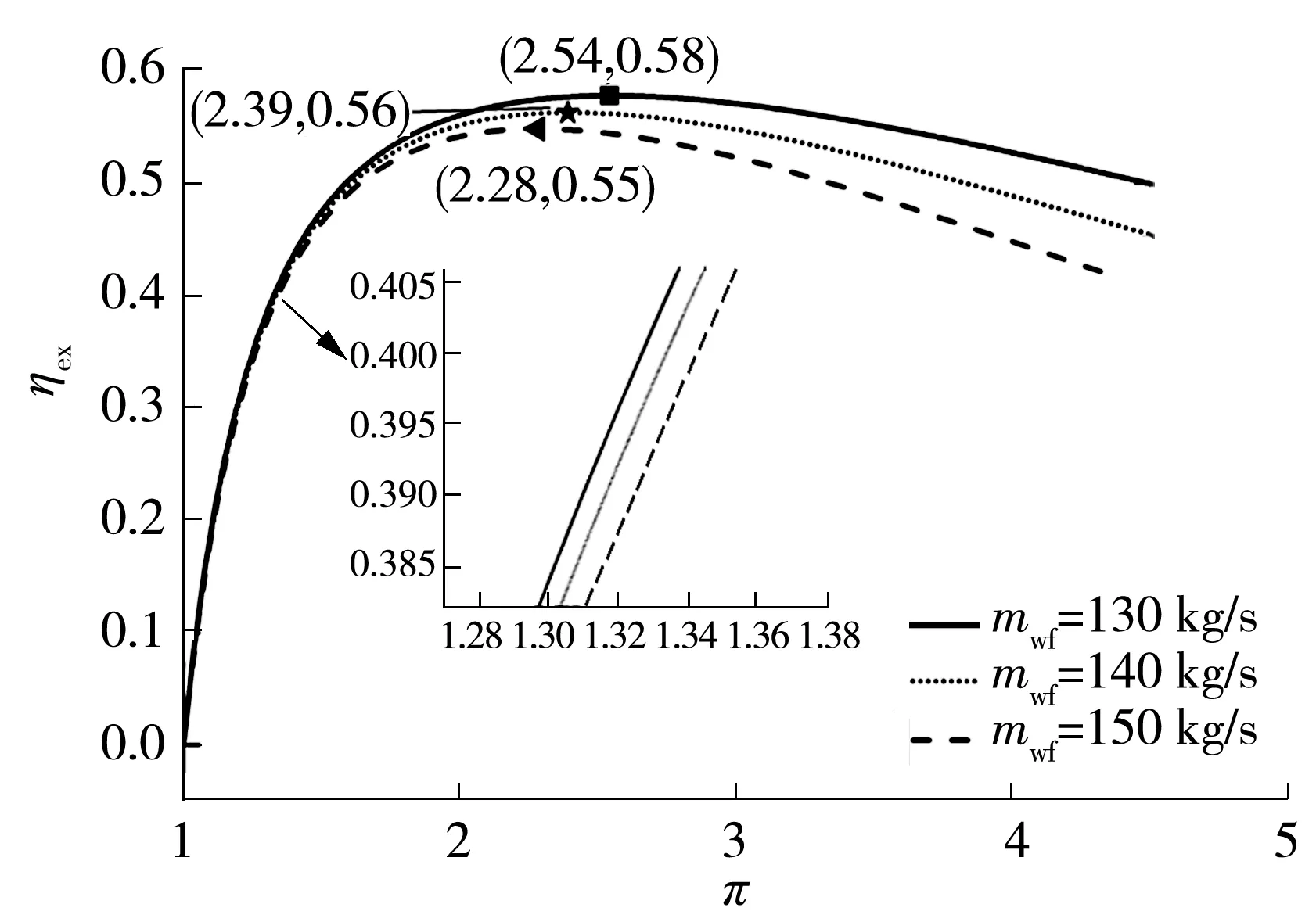
图4 mwf对ηex-关系的影响Fig.4 Effect of mwf on ηex- relation

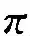
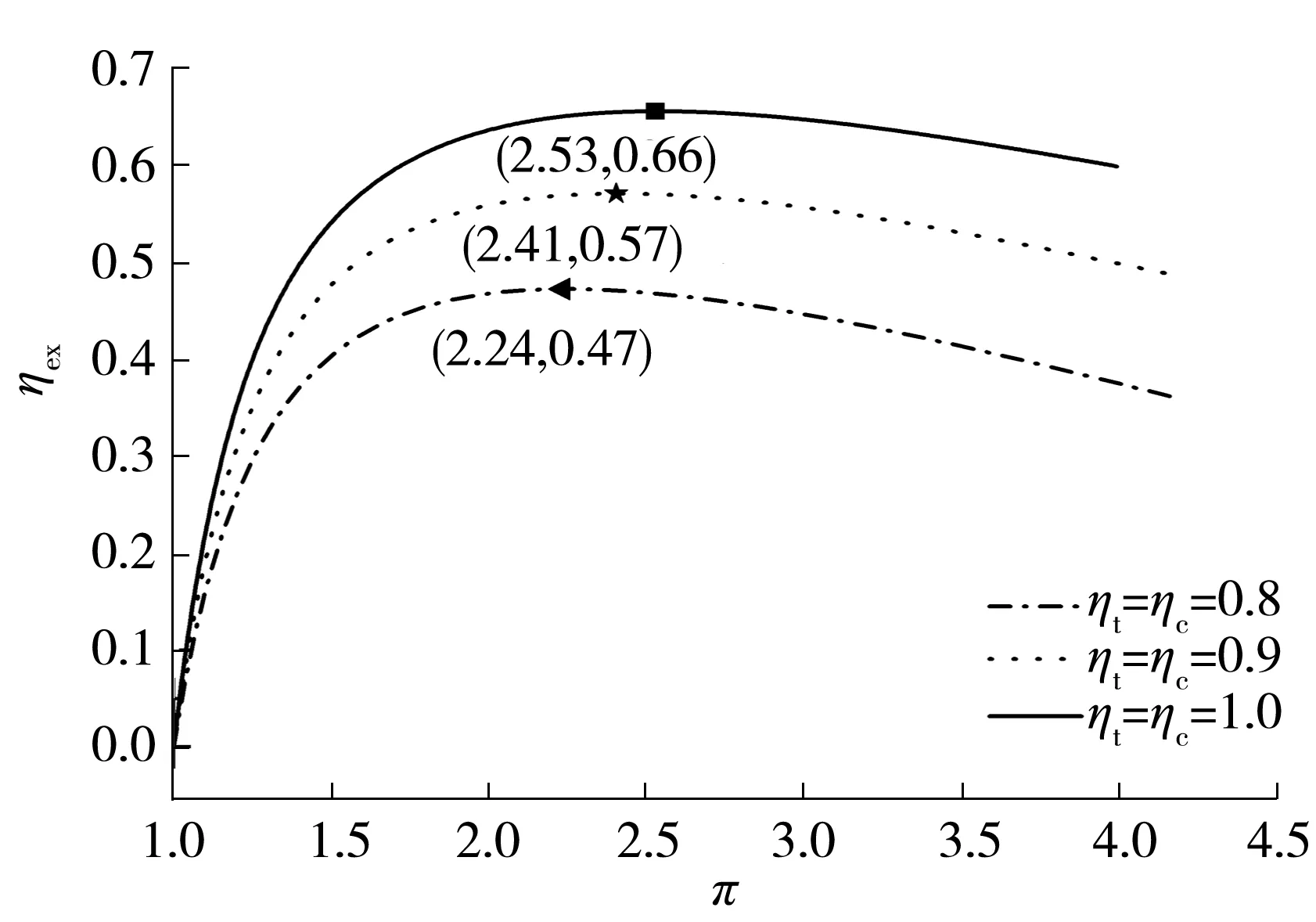
图5 ηt、ηc对ηex-关系的影响Fig.5 Effects of ηt and ηc on ηex- relation

图6 UT对ηex-关系的影响Fig.6 Effect of UT on ηex- relation

2.3 循环性能优化

根据文献[27- 28]对于以理想气体为工质的闭式布雷顿循环的研究结果，可进一步优化S-CO2布雷顿循环换热器的热导率分配以及热源与工质之间热容率的匹配关系。本节将以表3中相关参数为计算的初始设计点，其中ΨR、ΨH、ΨL分别为0.7、0.1、0.2，在给定约束UT=3 000 kW/K的条件下，以式(13)中效率ηex为目标进行优化。图7给出了工质质量流率为100 kg/s、压比为4.9时，循环效率ηex与加热器热导率分配比ΨH、回热器热导率分配比ΨR的三维关系。由图7可见：随着回热器热导率分配比的增大，效率呈先增大后减小的变化趋势；随着加热器热导率的增大，效率呈先增大后减小的变化趋势。上述变化趋势表明，在工质质量流率和压比一定时，存在最佳的加热器、回热器、冷却器的热导率分配比，使循环效率最大。图8给出了循环效率与压比、工质质量流率的三维关系。由图8可见，若进一步释放工质质量流率和压比的取值约束，还可以进一步提升循环效率，并且存在最佳工质质量流率和压比，使效率达到极大值。

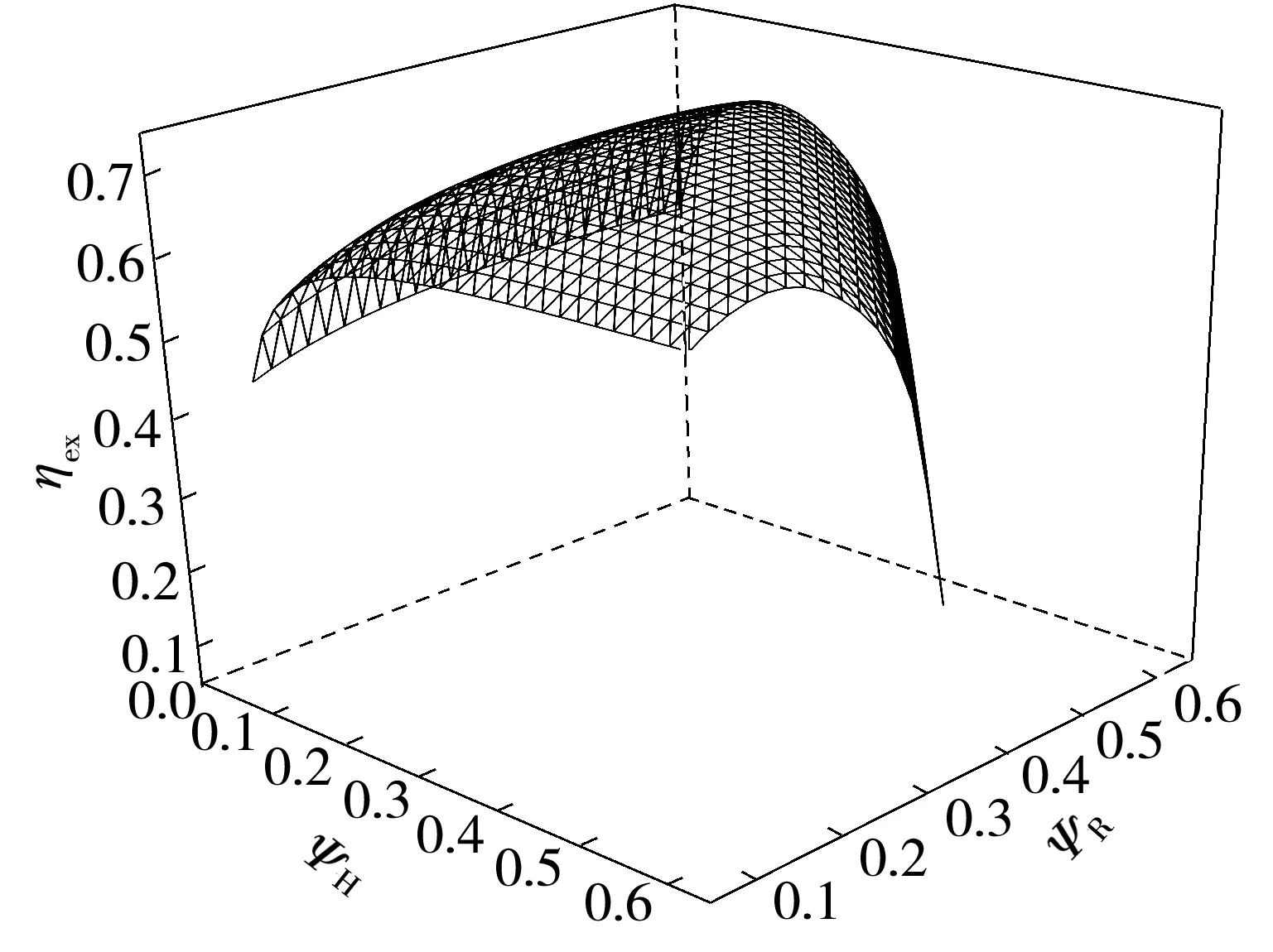
图7 ηex与ΨH和ΨR的三维关系Fig.7 Three-dimension relationship among ηex, ΨH and ΨR

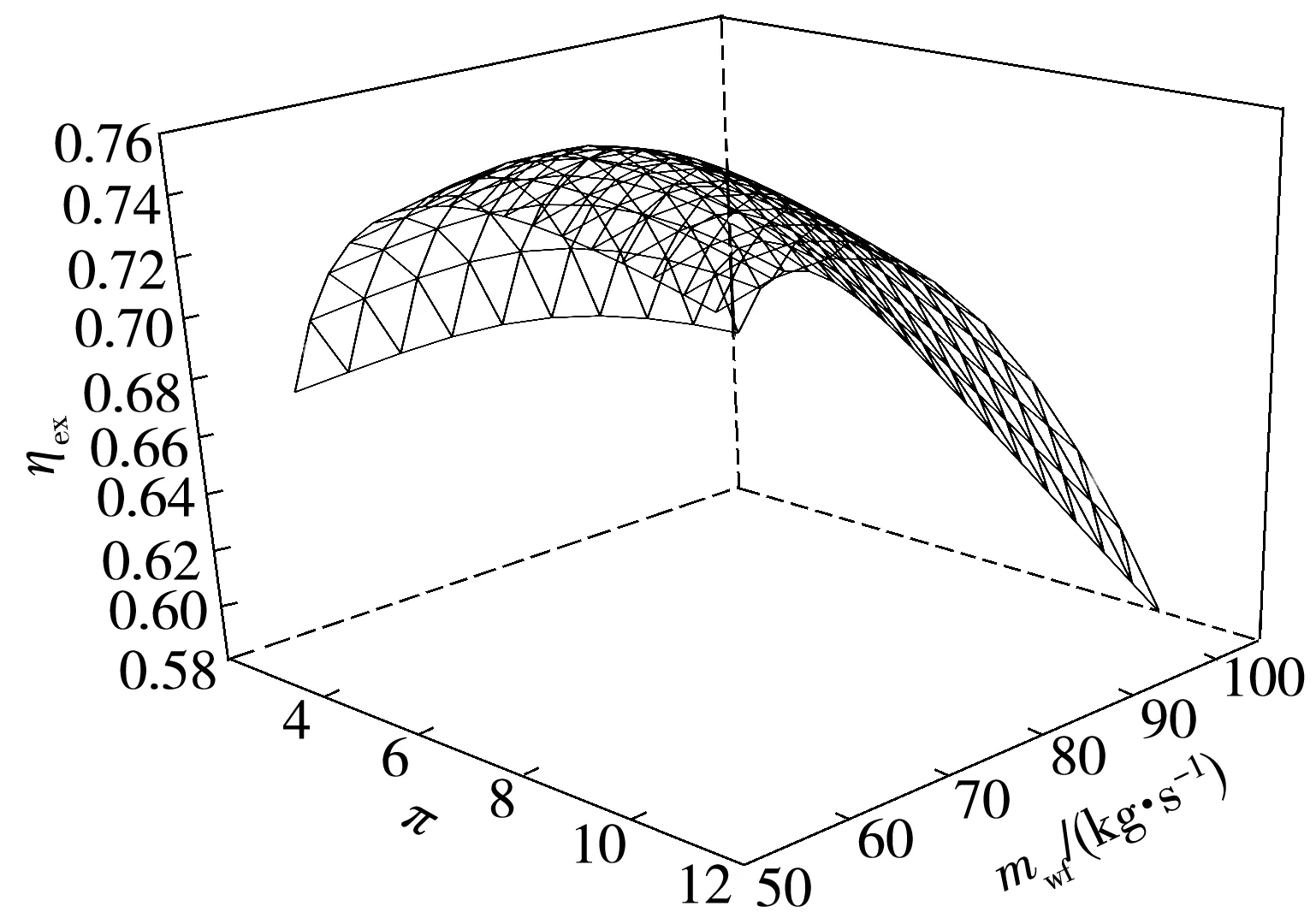
图8 ηex与mwf和的三维关系

表4给出了基于初始设计点得到的优化计算结果。由表4可知，在压比与工质质量流率不变的情况下，对换热器热导率分配比优化后，效率相比初始设计点提高了11.47%，且与初始设计点所给定的热导率分配比相比，加热器热导率分配比增大，回热器热导率分配比减小，这说明初始设计点的热导率分配比存在较大的优化提升空间。进一步释放压比取值约束，同时对压比和热导率分配比进行优化后，循环最大效率所对应的最佳压比增大为3.2，效率相比初始设计点提高了11.70%。由上可见，热导率分配比以及压比均为影响循环性能的重要参数。接下来，根据图8的结果，为获得循环效率的进一步提升，在已释放热导率与压比取值约束的基础上，进一步释放工质质量流率取值约束，求解循环效率最大值及相应的工质质量流率、压比以及热导率分配比。

表4 基于设计点的优化计算结果Table 4 Optimization calculation results based on design point

图9和表5给出了以ηex,max为优化目标，以工质质量流率、循环压比、各换热器热导率为优化变量的优化结果。图10给出了ηex,max优化后，其所对应的压缩机入口温度、循环最高温度以及热源出口温度随工质质量流率的变化关系。

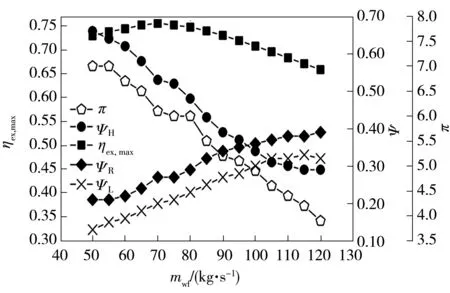
图9 ηex,max及相应的ΨH、ΨL、ΨR和随mwf的变化规律

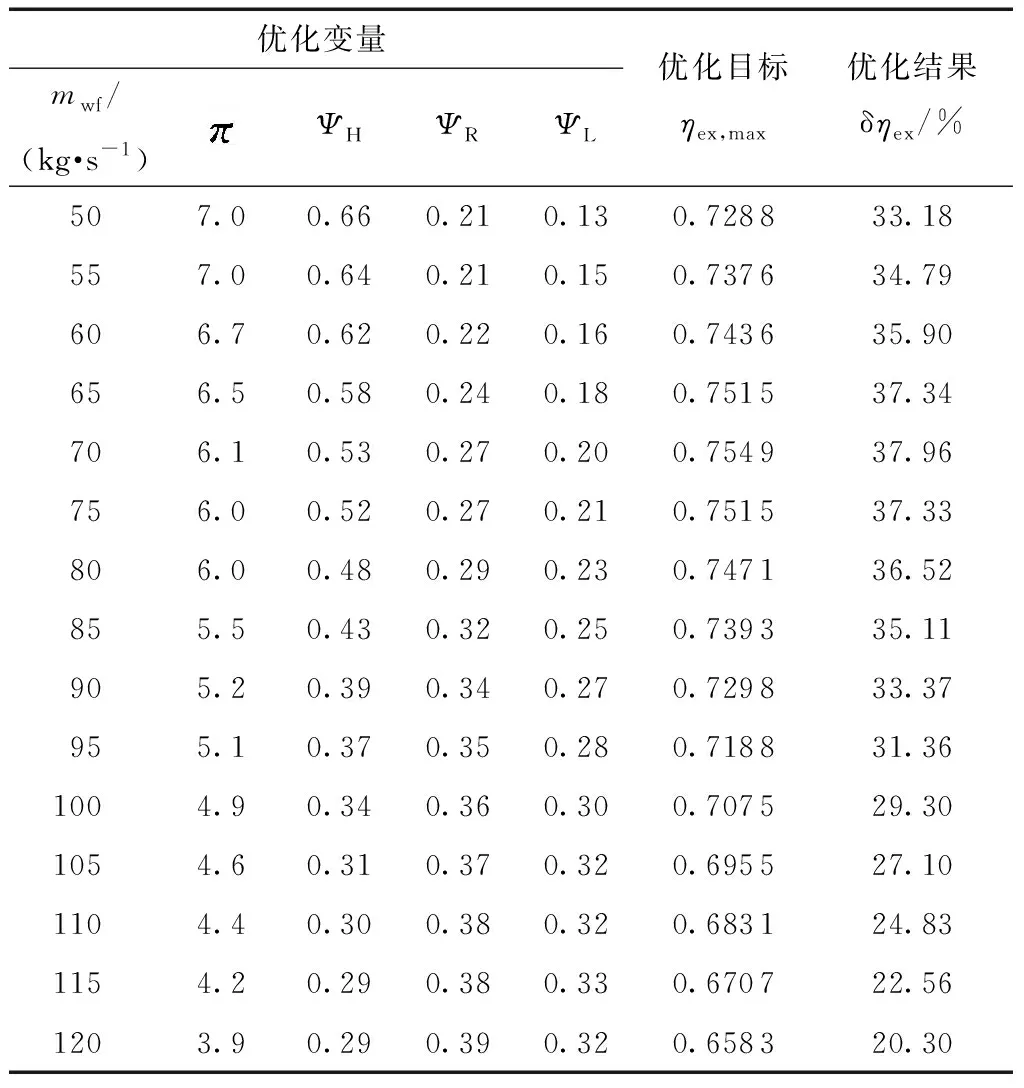
表5 以ηex,max为优化目标的计算结果

由图10可见，随着工质质量流率mwf的增大，ηex,max所对应的循环最高温度和热源出口温度呈减小的趋势，压缩机入口温度则保持在二氧化碳的临界点附近，这表明随着mwf的增大，高温烟气出口温度不断降低，循环从热源处的吸热量增大；虽然循环吸热量在增大，但mwf的增大使得工质温度提升同等温度区间所需要的热量也增大，循环最高温度的降低是吸热量增大与工质质量流率增大两者相互作用的结果。

图10 ηex,max所对应的T1、T4和TH,out随mwf的变化规律

3 结论

文中应用有限时间热力学理论建立了变温热源条件下的不可逆回热型S-CO2布雷顿循环模型，分析了工质质量流率、压比、总热导率、压缩机效率和透平效率对效率的影响，并在总热导率一定的条件下，以换热器热导率分配比、工质质量流率、循环压比为优化变量，以效率最大为目标进行了优化，进一步分析了工质质量流率对循环最高温度、热源出口温度的影响。

1)对于回热型S-CO2布雷顿循环，工质质量流率、总热导率、压缩机效率和透平效率对循环效率和压比的特性关系有较大影响。在工质质量流率、总热导率、压缩机效率和透平效率均一定时，存在最佳的循环压比，使循环效率取最大值；随着压缩机和透平效率的增大，循环中压缩机和透平的能量转换过程不可逆性均降低，循环最大效率及相应的最佳压比均增大；循环总热导率增大，循环中加热器、冷却器和回热器的传热不可逆性均降低，循环最大效率及相应的最佳压比均增大。

2)文中参数取值范围内，在压比与工质质量流率取值均不变的情况下对换热器热导率分配比进行优化后，效率相比于初始设计点可以提高11.47%；进一步释放压比取值约束，同时对压比和换热器热导率分配比进行优化后，循环最大效率相比于初始设计点提高了11.70%；若进一步释放工质质量流率取值约束，同时对工质质量流率、压比和换热器热导率分配比进行优化，循环最大效率可比初始设计点提高37.96%。

3)相比于传统的热力学分析方法，有限时间热力学方法以减少系统不可逆性为目标，反映了不可逆性对实际热力系统的影响，这主要表现在换热器热导率以及换热面积的最优分配上，以基于此理论所构建的模型进行数值模拟，相比于经典热力学分析方法更加贴近实际，更具有工程意义。优化结果表明：存在最佳的换热器热导率分配比、循环压比和工质质量流率，使得回热型S-CO2布雷顿循环的效率达到最大；随着工质质量流率的增大，可通过降低循环压比、降低加热器热导率、增大回热器热导率、增大冷却器热导率等方式来提升循环的效率。

除去增添了传热不可逆性、有限温差传热的影响外，文中模型同其他现行的动力工程循环模型一样具有较强的普适性，所得到的定性和定量研究结果可为实际S-CO2布雷顿循环的最优设计与运行提供理论指导。