基于干扰观测器的状态受限多缸同步控制策略

王云飞 赵继云 满家祥 丁海港

(1.中国矿业大学 安全工程学院，江苏 徐州 221116；2.中国矿业大学 机电工程学院，江苏 徐州 221116；3.徐州工程机械集团有限公司，江苏 徐州 221116)

随着社会的发展，工业设备朝着大型化和重型化方向发展以提高生产效率，但受制造工艺的限制，单执行器的尺寸往往无法满足大型设备的工作要求，因此多执行器协同系统在近几年得到了越来越多的关注[1- 3]。电液系统由于单位质量输出功率大和布置空间灵活的优点，经常被用于多执行器系统的驱动系统中。当前多执行器系统的电液控制系统主要采用同步控制，包括位置同步控制、速度同步控制和力同步控制，并已广泛应用于压铸机、盾构机等大型工程机械中[4- 5]。

最初的同步控制采用机械刚性连接的方法，但是存在精度差、安装困难的缺点。采用分流集流阀等液压元件实现同步控制具有安装方便的优点，但是抗扰能力差、执行器数量少[6]。随着控制理论的发展，众多学者开始利用电液控制策略来提高多执行器系统的轨迹跟踪精度和同步精度。根据Lorenz等[7]和Koren[8]提出的两大同步控制理论，多执行器系统同步控制技术一般被划分为基于单通道模型的同步控制技术和基于多通道模型的同步控制技术。基于单通道的同步控制技术主要有“等同方式”和“主从方式”,其中“等同方式”是指多个需要同步控制的执行元件同时跟踪同一理想输入，具有结构简单、控制方便的特点，在实际中得到了推广及广泛应用[9- 10]。基于多通道模型的同步控制技术可以分为多通道解耦同步技术和交叉耦合同步技术，具有同步精度高的优点，但由于要对多执行器进行解耦分析，因此控制器设计复杂，不适合应用在执行器数量较多的系统中[11- 12]。

此外，电液系统自身的强非线性、多执行器系统的偏载问题和外来干扰也给系统的精确控制带来了困难。目前，处理不确定问题和外干扰问题应用较多的是自适应鲁棒控制和干扰观测器控制[13- 14]。自适应鲁棒控制通过对系统参数进行实时调节，并利用鲁棒项来补偿外干扰，从而提高系统的控制精度。干扰观测器则将系统的参数不确定性和外干扰视为一个集成扰动项，通过设计观测器对其进行估计和补偿，具有结构简单、控制精度高的优点。为了进一步提高控制精度，学者们提出了对最大输出误差进行限制的输出受限控制方法[15- 16]。

结合以上分析，文中针对一类多缸同步控制系统，提出了基于等同控制的同步控制策略，设计了干扰观测器对每一路执行器回路的集成力扰动进行估计和补偿，通过对每个液压缸的输出位置误差和速度误差进行限制来提高多缸之间的运动同步度和整体的跟踪精度，利用鲁棒项来补偿系统中的压力-流量扰动，并利用障碍李雅普诺夫理论对系统的稳定性进行验证。

1 系统模型

文中以液压支架群同步拉架过程为模型，其原理如图1所示。液压支架的推移油缸系统实质为阀控非对称缸，由于其在同步拉架过程中不存在相互耦合关系，而且每个液压缸的尺寸型号都相同，因此可以一起对其进行讨论。系统无杆腔的油液压力p1、有杆腔的油液压力p2和输出位移y通过信号传感器进行测量，并反馈到控制器中。控制器通过输出电压u来改变伺服阀的主阀芯位移，从而使得质量块(其质量为m)的轨迹尽可能地跟随期望轨迹。

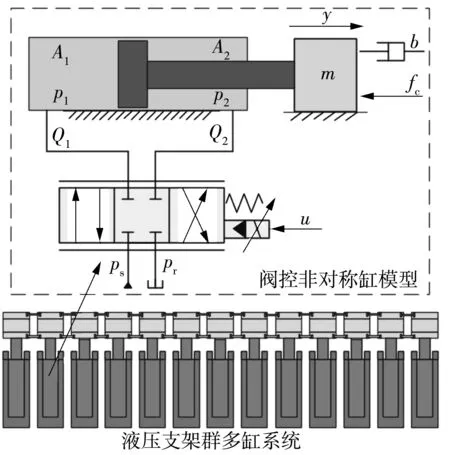
图1 液压支架群同步拉架示意图

非对称缸的力学方程为

(1)

式中，A1和A2分别为非对称缸无杆腔和有杆腔的作用面积，b为黏性阻尼系数，fc为外负载力，Fd为系统的建模误差(包括不确定参数、未建模摩擦力等)。

比例伺服阀的流量方程为

(2)

式中，Q1和Q2分别为非对称缸无杆腔和有杆腔的流量，kq为比例伺服阀的流量增益系数，xv为比例伺服阀的主阀芯位移，ps为系统供液压力，符号函数sgn(*)可以进一步表示成

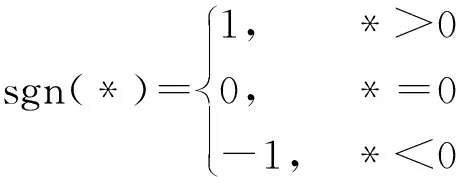
(3)

由于比例伺服阀的响应频率比整个电液伺服系统的响应频率快得多，因此将比例伺服阀的主阀芯位移与控制器的输入电压视为一阶比例关系：

xv=kvu

(4)

式中，kv为伺服阀主阀芯的位移-电压增益系数。

随着密封技术的提高，外泄漏系数在建模时通常可以被忽略，因此非对称缸的流量连续性方程为

(5)

式中，βe为液压油的体积弹性模量，V01和V02分别为非对称缸无杆腔和有杆腔的初始体积，Ct为系统内泄露系数，Qe1和Qe2为非对称缸无杆腔和有杆腔流量的建模误差(包括不确定参数、未建模动态等)。

将系统的状态变量定义为

则式(1)-(5)可以重新整理成以下形式：

(6)

式中，

2 控制器设计

控制器的设计原理如图2所示。首先设计干扰观测器对系统的集成力扰动进行估计和补偿，然后利用障碍李雅普诺夫函数对系统的位置误差和速度误差进行限制，并引入动态面对整个控制器的设计过程进行简化，最后对系统的稳定性进行验证。

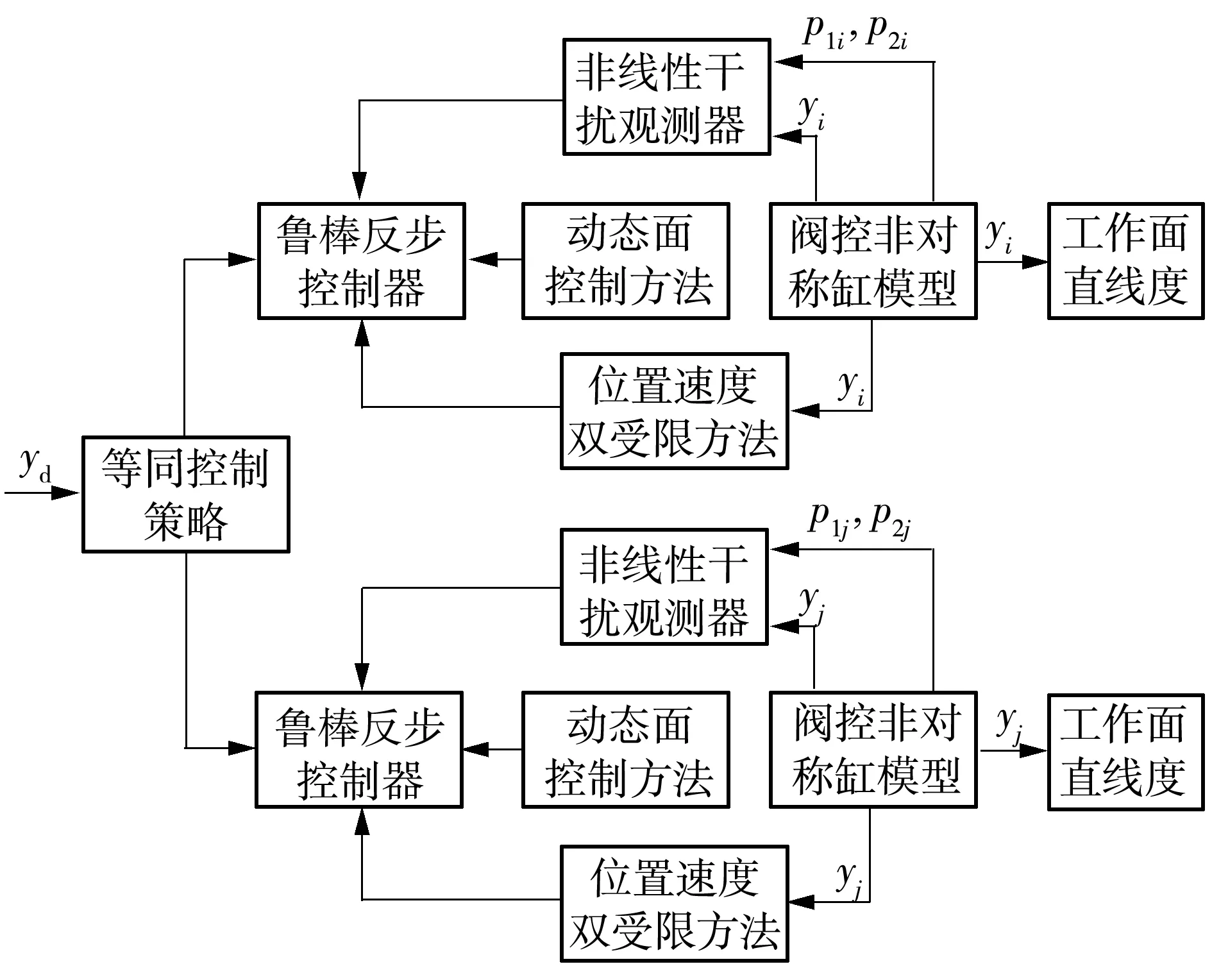
图2 同步拉架时多缸位置控制器的设计原理示意图

2.1 干扰观测器

定义文中所设计的非线性干扰观测器的估计误差为

(7)

设计非线性干扰观测器为[17]

(8)

式中，ε1为干扰观测器的增益。

由式(8)可知，若想抑制干扰观测器的变化，需要为其设计一个相对高的增益，但由于式(8)中存在系统状态的导数，较大的增益同时放大了传感器的测量噪音。为了降低测量噪音的影响，引入如下辅助变量：

(9)

对式(9)求导，则有

(10)

由式(10)可以看出，引入辅助变量后，在计算辅助变量的导数时可以避免对状态量进行求导，从而降低了放大测量噪音的风险。

对干扰观测器的估计误差求导，则有

(11)

可以将式(11)视为一个典型的一阶线性非齐次微分方程，其通解可以表示成

(12)

式中，d1(0)为扰动的初始值，d1max为扰动的最大值。

可以发现，ε1的值越小，扰动最终值的界值就越小，因此可以通过适当选取干扰观测器的参数来改变其观测性能。

2.2 动态面控制器

由于液压支架的数量众多，而且多缸拉架过程中并无耦合作用，所以多缸系统的同步控制采用同等控制。此外，多缸拉架是典型的多阀控多缸系统，因此仍可以以其中第j号缸为例进行动态面控制器的设计。

步骤1定义位置/输出跟踪误差e1j为

e1j=x1j-yd

(13)

式中，yd为多缸系统同步运动的期望轨迹。对式(13)求导，则有

(14)

为了保证多缸系统与期望轨迹之间的准确跟踪，设置最大位置跟踪误差值为kb1j，且有|e1j|≤kb1。

定义障碍李雅普诺夫函数为

(15)

对式(15)求导，则有

(16)

为了保证式(16)的负定性，选取x2j的虚拟输入α1j为

(17)

式中，k1j为正常数增益。

(18)

定义滤波器的输出值和原始虚拟输出值之间的误差为

(19)

该误差的动态方程为

(20)

步骤2定义第2个动态面的误差为

(21)

求e2j的时间导数，则有

(22)

为了进一步提高多缸系统的位置跟踪精度，并提高其速度的控制精度，对速度跟踪误差也引入1个最大误差限制kb2，选取障碍李雅普诺夫函数V2j为

(23)

对式(23)求导，则有

(24)

与步骤1相似，为了保证式(24)的负定性，选取x3j的虚拟输入α2j为

(25)

式中，k2j为正常数增益。

(26)

定义两者之间的误差为z2j，则

(27)

误差的动态方程可以表示成

(28)

步骤3定义动态面的最后一个误差为e3j，则有

(29)

式(29)的时间导数为

(30)

选取李雅普诺夫函数V3j为

(31)

选取整个系统的实际输入为

(32)

式中，d2jmax为系统压力-流量扰动的最大值。

根据液压系统的实际工况，反步控制中的各项虚拟输入α1j和α2j都是有界的，而且其经过一阶滤波器的输出同样有界。此外，它们的各项微分也是有界的。

2.3 稳定性证明

为了保证整个系统的稳定性，选取第j号缸的李雅普诺夫函数为

(33)

结合上述公式，对式(33)求导，则有

(34)

根据式(20)，有以下不等式成立：

(35)

所以，有下式成立：

(36)

根据杨不等式，可以推导出以下不等式成立：

(37)

式中，M1j和M2j分别为虚拟输入导数的最大值。

此外，根据杨不等式，由式(34)中的其他各项可以推导出以下不等式：

(38)

又因为

e3jd2j-d2jmax|e3j|≤|d2j|·|e3j|-d2jmax|e3j|≤0

(39)

式(34)可以重新整理成

(40)

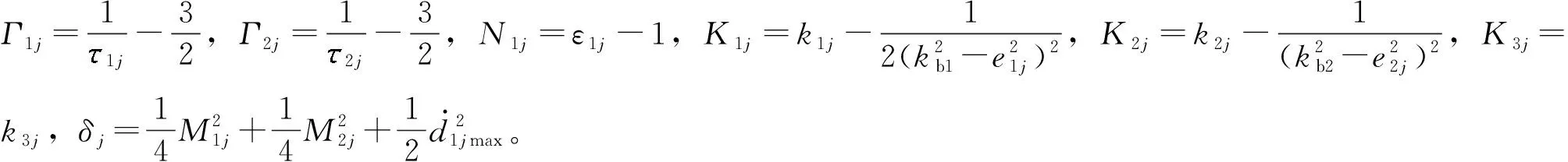
式(40)可以写成标准的一阶线性非齐次微分方程的形式：

(41)

式(41)中，各项的详细表述为

aj=min{K1j,K2j,K3j,Γ1j,Γ2j,N1j}

(42)

式(42)的通解可以表示成

(43)

由式(43)可以看出，随着时间的延长，Vj将收敛于一较小值μj，而μj的值取决于δj/(2aj)。如果选取aj≥δj/(2μj)，则式(41)为负定的，也就说明整个系统是渐进稳定的。因此，通过合理地选取干扰观测器及动态面控制器的各项参数，可以保证多缸同步拉架系统的稳定性。

3 仿真验证

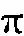
表1 仿真模型的主要参数Table 1 Main parameters of the simulation model

C1控制器(对比控制器1)：比例-积分控制器，比例增益kp=300，积分增益ki=10。

C3控制器：基于非线性干扰观测器的位置速度受限鲁棒动态面控制器，其控制参数与C2控制器完全相同，额外的位置最大误差kb1=0.005，速度最大误差kb2=0.2。

图3示出了在C1控制器控制下，不同负载力时运动双缸的轨迹跟踪情况和跟踪误差情况。可以看出：C1控制器控制下，两个推移油缸的最大跟踪误差都在25 mm左右，而且两个缸的最大跟踪误差都出现在运动速度最快的时候，此时产生了略微的抖动；此外，不同的负载力对液压缸的控制精度会产生影响。

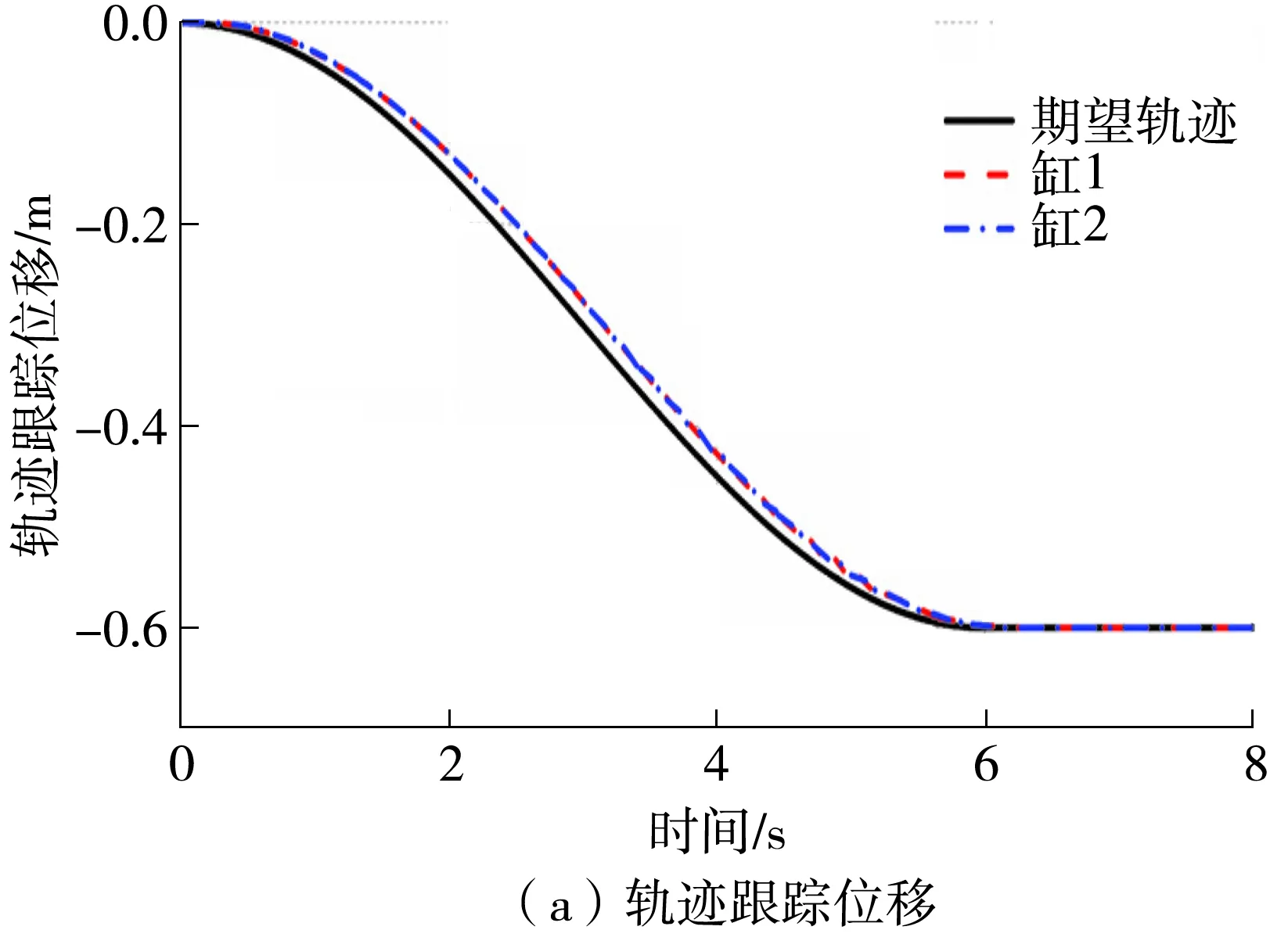
图4和图5分别示出了C2和C3控制器的控制情况。C2和C3控制器具有非线性干扰观测器，它们对未知负载力进行实时估计并反馈给主控制器进行补偿，因此最大跟踪误差较小。C2控制器控制下，两个缸的跟踪误差都在3 mm左右，不仅跟踪曲线在整体上与期望轨迹的曲线相重合，而且误差曲线也十分接近，说明同步运动的两个推移油缸的同步精度较高。而加了位置限制和速度限制的鲁棒动态面控制器C3的跟踪误差进一步减小，两个缸的跟踪误差都仅有0.04 mm，位置控制精度进一步提高，而且由于运动速度误差受到限制，同样提高了两个缸的运动同步度，但是误差曲线略有抖动，这是由位置速度的受限控制引起的。

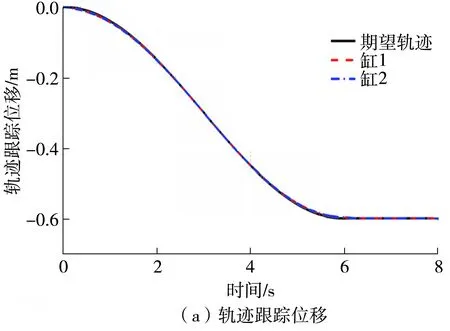
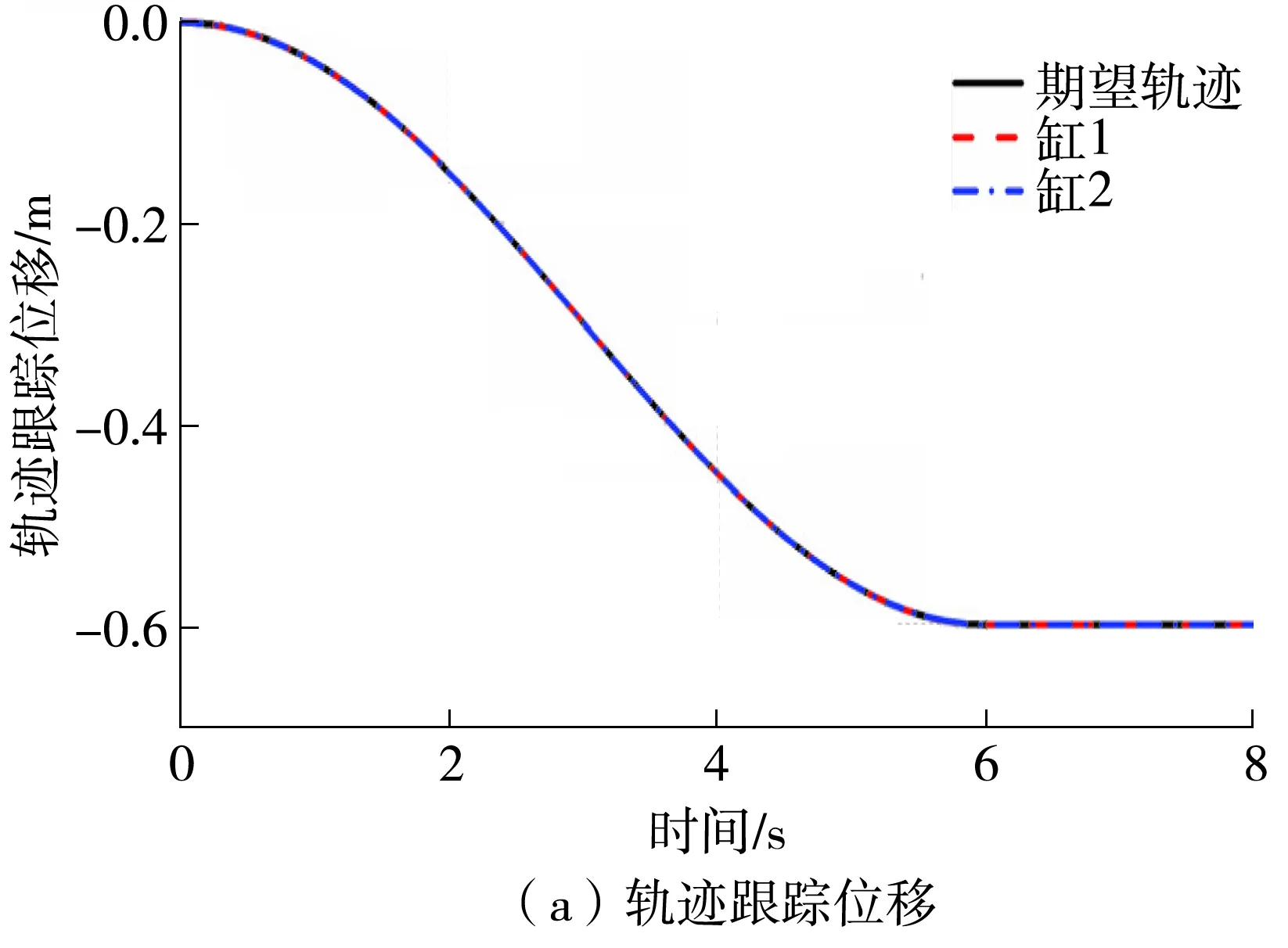
图6示出了不同控制器下两个缸的同步误差。从图中可以看出：C1控制器的同步误差最大，约为5 mm，而且整体的震荡很大。C2控制器的同步误差约为0.4 mm，而C3控制器的同步误差约为0.06 mm。这是因为运动双缸不仅位置误差受到限制，运动速度也受到了限制，这保证了运动双缸的一致性。通过分析运动双缸的轨迹跟踪误差图和同步误差图可见，在所提出的同等控制策略下，基于非线性干扰观测器的位置速度双受限动态面控制器是有效的，它不仅大大简化了控制器的设计，而且提高了单缸的位置控制精度和两个缸的同步控制精度，同时提高了系统的抗扰能力和鲁棒性。

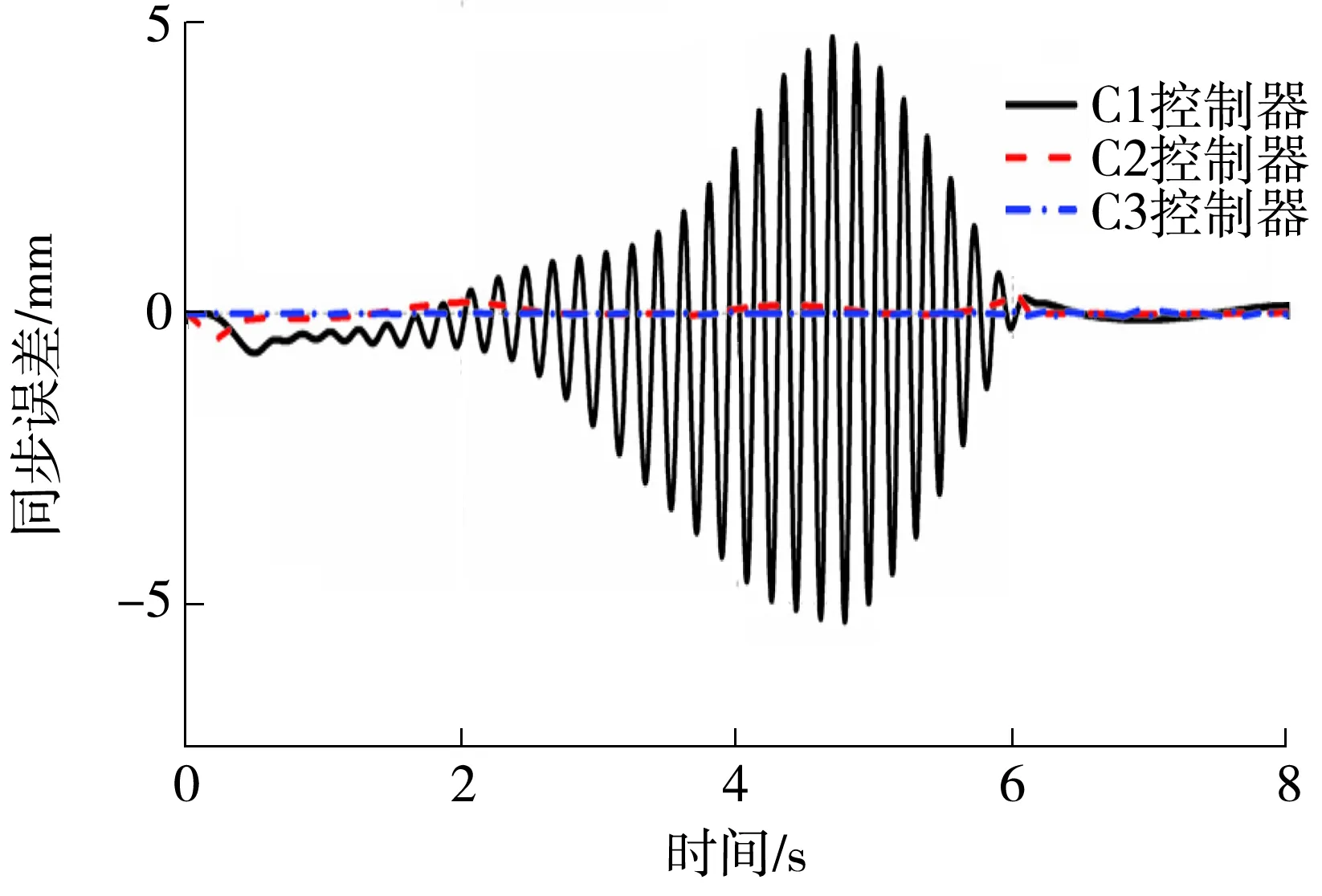
图6 不同控制器的同步误差Fig.6 Synchronization error of different controllers

图7示出了运动双缸的干扰观测器观测结果。可以看出，虽然不同推移油缸受到的负载力不同，但是非线性干扰观测器都能比较准确地对其进行估计，进而反馈给控制器进行补偿，从而提高了系统的抗扰能力，并提高了推移油缸的位置控制精度。

4 实验验证

为了进一步说明文中提出的多缸拉架控制算法的优越性，搭建了图8所示的多缸系统实验台(具体参数如表2所示)，设计了2个对比控制器来进行对比试验。下文给出了控制器的参数设置。

图8 多缸系统模拟实验台Fig.8 Simulation test bench of multi-cylinder system

PI控制器(对比控制器1)：比例-积分控制器，比例增益kp=150，积分增益ki=20。比例增益影响PI控制器的响应速度，虽然比例增益越大系统响应越迅速，但是过大的比例增益会导致系统的震荡，积分增益有助于调节、改善系统的稳态误差。

NOBR控制器(对比控制器2)：基于非线性干扰观测器的鲁棒控制器，其中非线性干扰观测器的观测增益ε1=200，鲁棒控制器的控制参数k1=100、k2=60、k3=60，鲁棒项幅值d2max=5。

表2 试验台的主要物理参数Table 2 Main physical parameters of the test bench

由于实际系统的动作较慢，因此选择低频信号作为期望轨迹，这样即使在动态情况下，由于干扰观测器对外来干扰的实时估计和补偿作用，也能提高系统的抗扰能力和控制精度。图9分别示出了在PI控制器控制下，不同负载力时运动双缸的轨迹跟踪情况和跟踪误差情况。可以看出，PI控制器控制下，两个缸的最大跟踪误差均约为7 mm，都出现在运动速度最快的时候，而且不同的负载力对液压缸的控制精度影响较大。

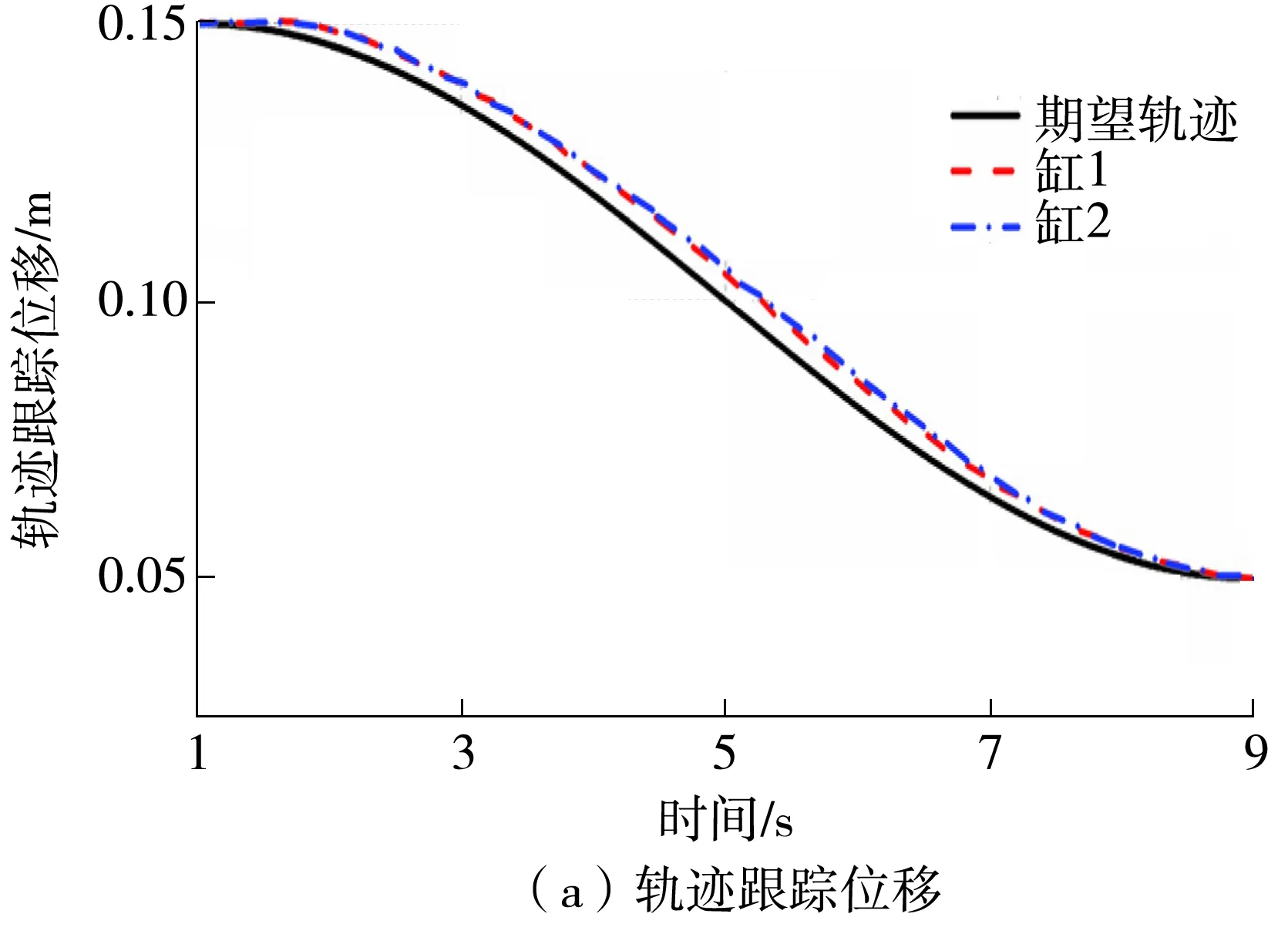
图10和图11分别示出了NOBR和NOBECR控制器的控制情况。NOBR和NOBECR控制器具有非线性干扰观测器，它们对未知负载力进行实时估计并反馈给主控制器进行补偿，因此最大跟踪误差较小。NOBR控制器控制下，两个缸的跟踪误差均约为6 mm，跟踪曲线整体上与期望轨迹的曲线相重合。而加了位置限制和速度限制的鲁棒动态面控制器NOBECR的跟踪误差仅约2 mm，位置控制精度进一步提高，而且由于运动速度误差受到限制，同样提高了两个缸的运动同步度。

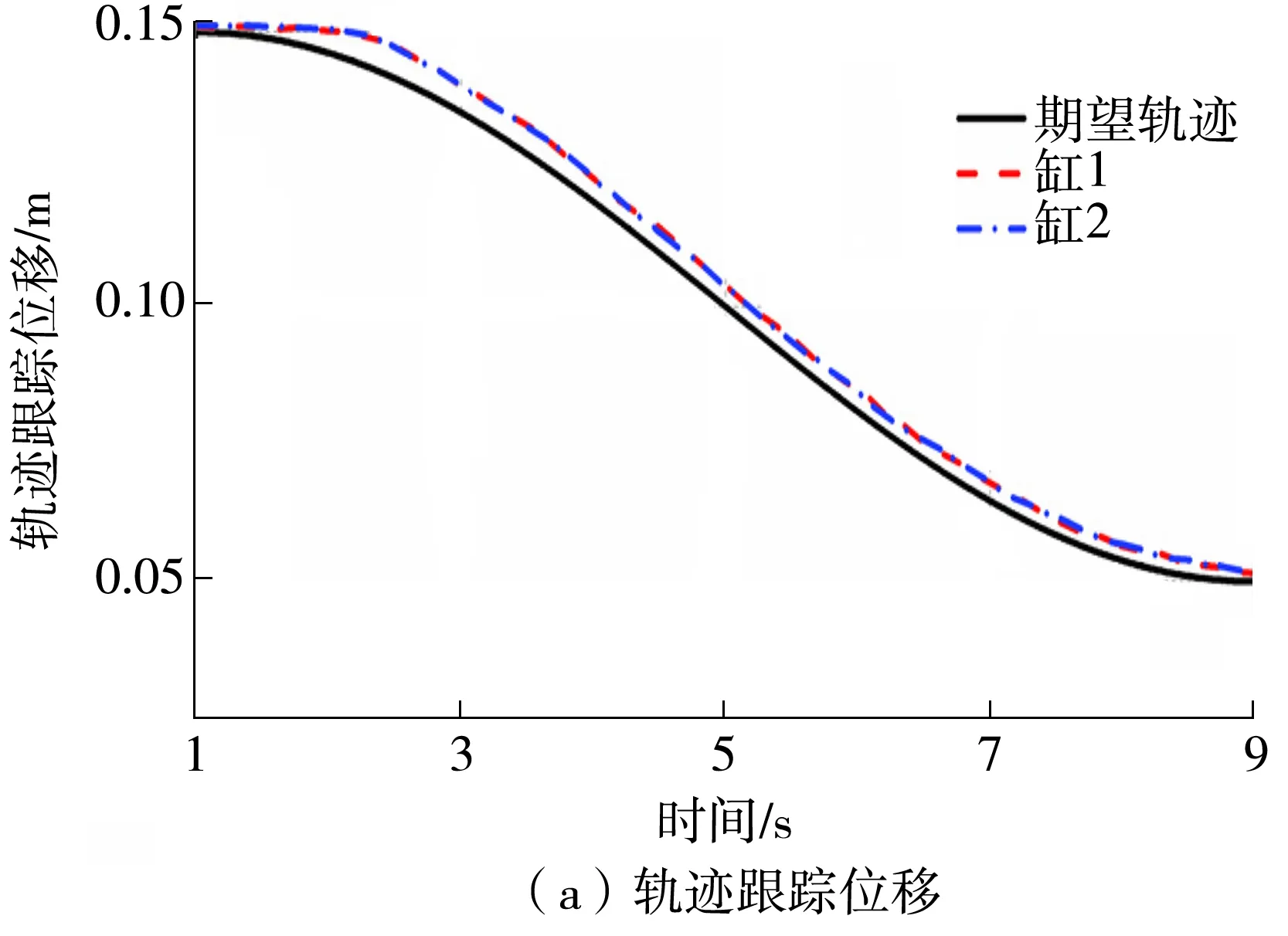
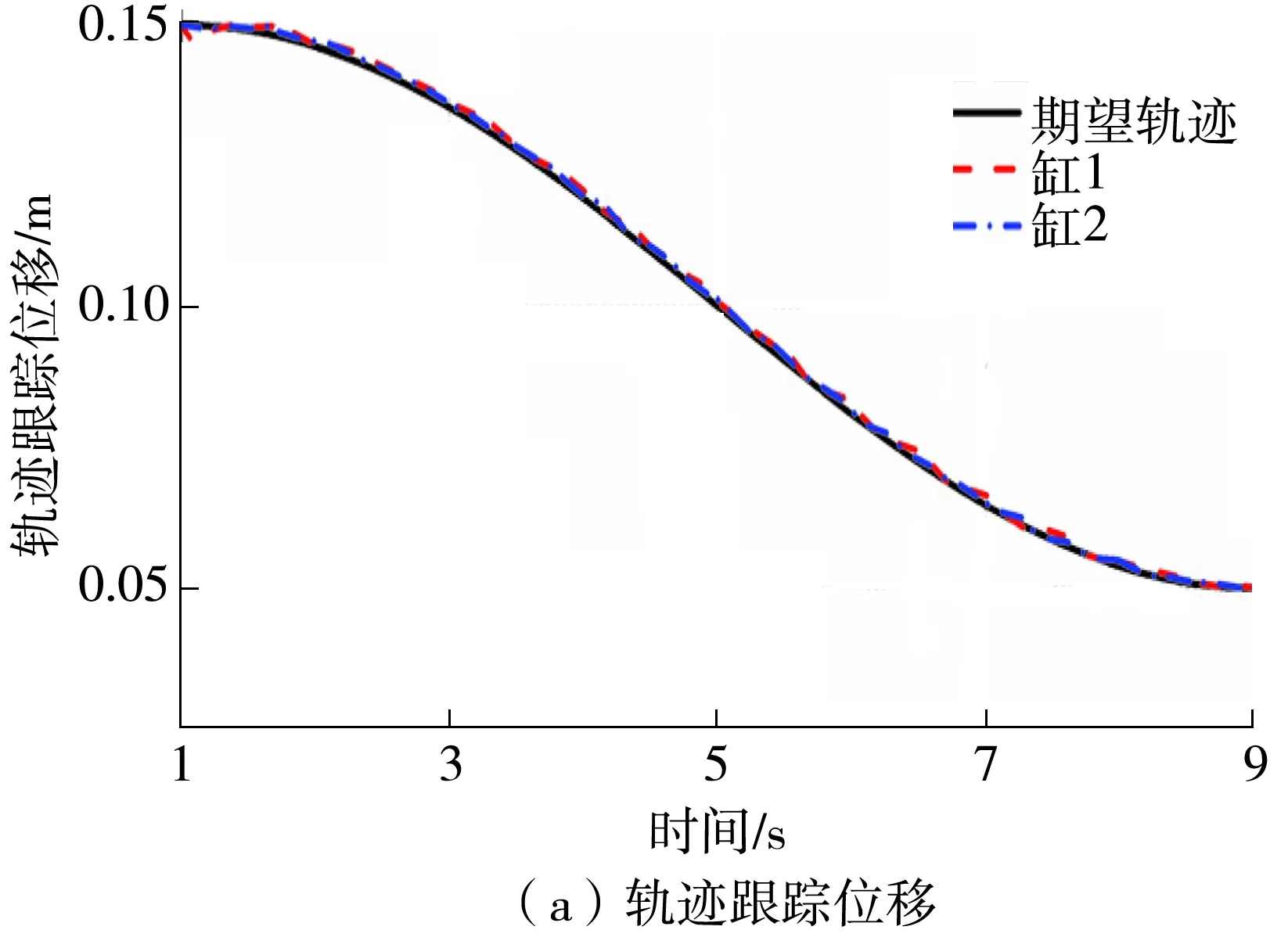
图12显示的是3种控制器下运动双缸的同步误差。可以清楚地看出，两个缸的同步误差相差不大，其中PI控制器下的同步误差最大约为2.2 mm，NOBR控制器下的同步误差约为1.4 mm，NOBECR控制器下的同步误差约为0.8 mm。虽然同步误差的数值相差不大，但是采用NOBECR控制器时具有更小的波动，因此跟踪效果更好，精确度更高。图13所示为非线性干扰观测器对双缸系统的力扰动估计，由于缸1的加载力稍大，因此在运动初始时有个较大的跳跃性，之后的估计值较为平稳。

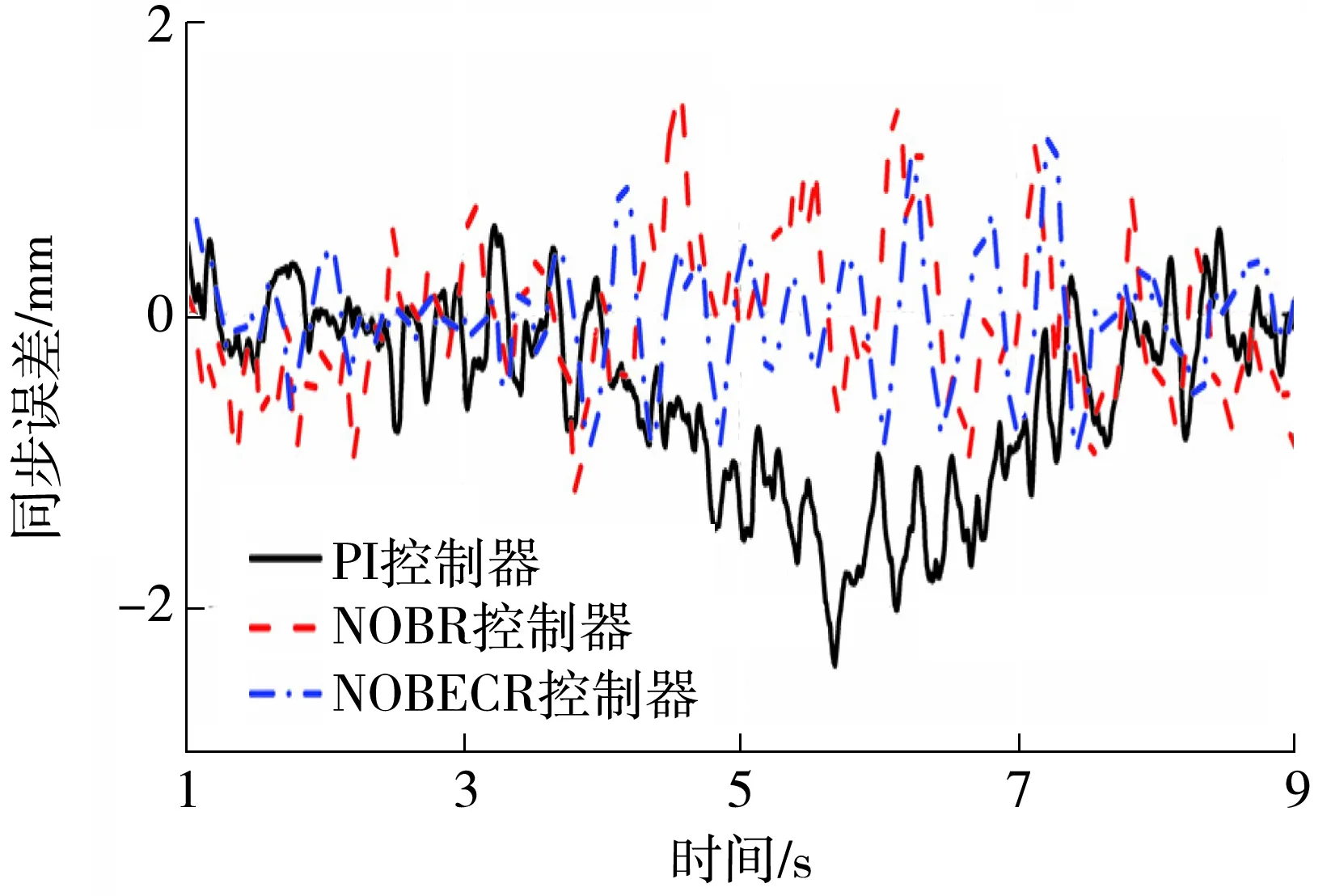
图12 运动双缸的同步误差Fig.12 Synchronization errors of the two pulling cylinders

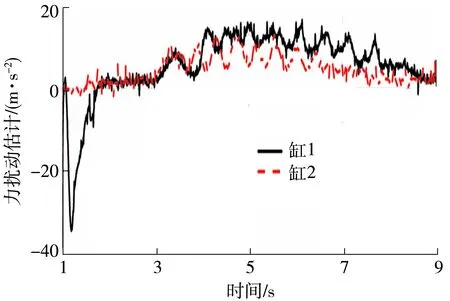
图13 运动双缸对集成扰动力的估计

5 结语

针对多缸同步控制系统，文中提出了一种基于干扰观测器的位置速度双受限鲁棒动态面等同控制方法；利用干扰观测器对集成力干扰进行估计和补偿，采用障碍李雅普诺夫函数对系统的位置和速度误差进行限制，并验证控制器的稳定性。实验结果证明，文中所设计的多缸同步控制器的系统波动更小，两个缸的同步误差约为0.8 mm，具有更强的抗扰能力和更高的控制精度。文中研究了一类多执行器的同步控制问题，在许多场合均有应用。下一步的研究将集中在改善控制器的性能和加强控制器的实际应用方面。