结合在线随机张量分解和全变分的运动目标检测*
喻丁玲, 杨国亮, 龚家仁
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
0 引 言
近年来,移动摄像机在生活中应用的非常普遍,在现代智能家居或安全防范中起着很重要的作用,所以高精度检测目标是非常必要的。移动摄像机由于镜头的移动,视频背景每一帧背景之间的相关性不是那么强,所以运动目标检测的准确性产生影响。
鲁棒主成分分析(robust principal component anahysis,RPCA)[1]由于其本身的优势在计算机视觉的很多工作中得到了应用。然而,它只在静态背景下能充分发挥其优势,考虑到现实环境的背景在本质上并不总是静态的,物体的运动也不匀速。为了克服传统RPCA模型中的不足,许多研究[2~4]都在RPCA模型的基础上进行修改,并取得了较好的效果。在此基础上,文献[5~8]将全变分(total variation,TV)正则化引入到稀疏性约束中,可以对视频的前景空间进行更有效的建模。随着视频检测的数据量越来越大,大量的研究[9~13]从二维转向三维,在张量模型上进行优化求解并取得了较好的效果。但上述采用张量的分解方法都是基于矩阵分解问题的泛化,此外,大多数增量张量子空间学习方法都将矩阵奇异值分解应用于展开矩阵,这无疑增大了计算复杂度。低秩矩阵恢复模型在处理视频序列时通常将三维数据排列为二维观测矩阵再进行分解,这种压缩[14]形式可能会破坏数据的原始结构。
张量可以更全面地表示数据各维度之间存在的结构联系信息,所以本文用向量和矩阵的高阶推广来表示数据,从而达到比RPCA模型更好的恢复效果。考虑到运动目标检测对检测实时性的要求很高,所以,采用在线随机张量分解(online stochastic tensor decomposition,OSTD)的优化方法实时更新,结合小样本批处理初始化缩小基矩阵大小,从而提高初始化效率,达到提升检测效率的目的。
1 基于OSTD的运动目标检测
假设Y=RI1×I2×I3是一个输入的三阶张量,Y中含有外部干扰,将张量数据分为低秩张量部分(背景)X和稀疏前景E之和,Y=X+E,所以,张量数据通过凸优化可写成如式(1)的形式
(1)

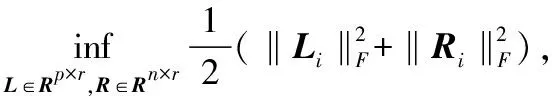
(2)
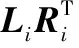
(3)
2 基于OSTD和TV的运动目标检测
2.1 问题建模
视频前景中的移动物体在连续帧之间是连续的,并且每帧的移动物体在空间域的局部区域也是平滑的,这种先验称为视频前景的时空连续性,将各向异性全变分正则化施加于U,可以实现对前景平滑度的正则化,各向异性TV[14]正则化的定义为
(4)
式中 (Dhu,Dvu,Dtu)T为l1或l2,1范数,本文用‖Du‖2,1为U的各向异性TV范数。由于本文研究环境复杂,要充分考虑到稀疏前景矩阵不仅包含运动目标,而且还包含动态背景,故在稀疏前景部分令E=U。结合前文所述,使用TV正则化约束稀疏前景部分,所以,本文的运动目标检测模型如下
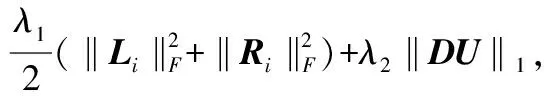
(5)
式中λ1,λ2为平衡参数因子,通过引入辅助变量M,式(5)可以等价地重新表示为
(6)
文献[9] 选用的初始化策略是手动定义初始化矩阵L0的大小,然后通过随机生成的方法来初始化,但这样的初始化会根据不同的场景进行改变,导致算法精度降低和运行时间长。通过研究L的性质发现,可以利用同样大小的张量数据子矩阵的低秩张量部分代替低维子空间的基来解决上述问题,所以,本文选用的初始化策略是将张量数据的前q帧作为一个子矩阵,然后通过小样本批处理方法求解L0来达到精确初始化的目的。具体的求解可以通过2.2节中的算法实现。
2.2 问题求解
首先对基矩阵进行初始化,选取部分帧作为初始化样本,再对基矩阵进行批处理初始化,本文选用的初始化方法是非精确增广拉格朗日乘子法
(7)
式中M∈Rp×q为由视频序列Y的前q张图片组成的,q为样本维数,M可分为低秩张量T和稀疏张量H之和,采用增广拉格朗日函数法求解如下
Lμ(T,H,Y,μ)=‖T‖*+λ‖H‖1+
(8)
利用交替方向法(ADMM),固定其它变量值为常数,每次只求出一个变量的最小值,从而得到近似解
(9)
通过求解式(8)和式(9)就可以得到低秩张量T,这里T被近似看成L0。接下来求解式(10)就可以得到本文的最优化解
(10)
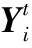

(11)
最后,给出了在t时刻更新的多维子空间张量X的i阶基Li矩阵的目标函数lt(L)

(12)
在这个过程中,对基矩阵部分系数r和稀疏前景部分的系数m进行优化,使损失最小化。求解式(6)、式(10)~式(12)便能获得张量数据序列的低秩张量部分和前景部分。
本文算法流程如下:
算法1OSTD和TV正则化算入:N阶张量数据Y=RI1×I2…IN

fort=1︰ndo(访问每个样本)
fori=1︰ndo

λ2‖m‖1
(13)
R(︰,t)←rt.计算每第i阶下At和Bt的累加矩阵
(14)
调用算法3更新Lt
(15)
End
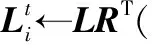
算法2基矩阵初始入:初始化基矩阵M∈Rp×r,
H0=0,μ0>0,ρ>1,k=0,λ
While not convergence do
(16)
Dk+1=USμ-k(∑)VT
(17)
(18)
Yk+1=Y+μk(M-Dk+1-Hk+1]
(19)
将μk更新到μk+1,k←k+1
End while
L0=Dk
输出:L0
算法3基矩阵更入L=[L1,…,Lr]∈Rp×r,A=[a1,…,ar]∈Rr×r
B=[m1,…,mr]∈Rp×r,←A+λ1I
forj=1︰rdo(访问L的每一列)
更新基矩阵L
(20)
End for
输出:L
通过算法1所示的方法使目标函数最小化;通过算法2进行基矩阵初始化操作,得到初始化基矩阵L0;按算法3对基矩阵L进行更新;最后重复算法迭代直到达到迭代次数或者所有样本完成计算。
3 实验结果与分析
实验在MATLAB 2018环境下实现,所选用的计算机为64位操作系统的笔记本电脑,8GB RAM,电脑处理器为Intel®CoreTMi5—8250U CPU@1.60 GHz 四核。选用了DAVIS数据集,DAVIS 数据集是典型的移动相机拍摄画面,包含50个不同的视频序列,每帧分辨率为854×480,每个序列都有给出了前景真实值。为了避免数据覆盖或丢失所有测试视频选用连续的20~40帧图像进行检测。
图1对比了三种其他算法和本文算法的检测效果图,选用的是DAVIS 数据集上4种不同序列,在相同条件下,将本文算法与近期其他三种同类方法(DNLRL1TV[8],OSTD[12],TUCKER[11])进行对比。第一行(a)是kite序列上的2th,第二行(b)是carround序列上的10th,第三行(c)是paragliding序列上的16th,第四行(d)为tennis序列上的26th,最后一行(e)是BMX-bumps序列上的29th;第一列到最后一列分别为:当前帧、Ground Truth、本文算法、DNLRL1TV算法、OSTD算法、TUCKER算法检测结果。从检测图1中可以看出,本文提出的方法检测出的运动目标更加完整,与真实前景值较为接近,在采用在线优化方法后能有效对背景变化实时更新,结合全变分正则化,始终能从移动的视频中对动态场景进行准确的目标检测。DNLRL1TV算法也能检测出较为完整的运动目标,但去噪性能较差,其他两种算法均错误地将一定的背景部分检测为前景目标,准确性和去噪性能差。

图1 不同算法检测效果
为了证明本文采用的初始化策略能有效提高检测速度,分别比较了上述4种算法在不同的5个序列上每帧的运行时间,如表1所示。本文方法、OSTD、DNLRL1TV、TUCKER算法的平均每帧处理时间分别为1.97,2.16,4.20,4.43 s。从每帧处理时间上分析本算法基本能满足检测类算法对运行速度的要求,而且检测的效果更佳。
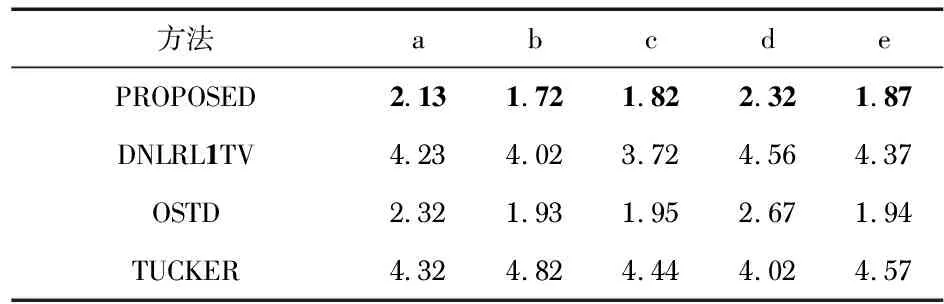
表1 每帧处理时间 s
用召回率、准确率和F-measure值来定量分析,令TP为准确检测出的前景部分的像素数目,TN为检测结果中正确检测出的背景部分像素,FN为被误检为前景的背景像素数目,FP为被误检的前景点像素数目,TP+FP为检测目标中的所有前景像素数目,TP+FN为真实前景像素数目。则本文采用的值指标表示为:召回率R=TP/(TP+FN);F-measure值F=2×P×R/(P+R);准确率P=TP/(TP+FP)。
表2为几种算法基于F-measure、召回率、准确率这三项指标来定量分析本文算法的性能,表中分别用F,R,P表示。F值越大,表明检测到的前景区域与地面真实前景区域越接近。

表2 各种算法的P,R,F值
4 结 论
本文通过采用初始化策略提高了初始化效率的同时还缩小了基矩阵大小,达到提高检测精度的目的。采用在线优化方法实现实时优化,能有效解决移动摄像机拍摄的视频背景帧变化的问题。在稀疏前景部分利用TV正则化约束目标的空间性和保持边缘的完整,再不断更新,直到达到设定的迭代次数或所有样本计算已经完成。并在移动摄像机视频序列DAVIS上进行了实验,实验结果表明:本文方法不仅能有效检测出运动目标,而且保持了较快的运行速度,为移动视频的实时处理提供了参考。

