基于改进MCKF的UWB/IMU室内组合定位算法*
廖天睿, 吴向东, 赵林惠, 金晓明, 贾之阳, 戴亚平
(1.北京联合大学 机器人学院,北京 100101;2.北京理工大学 自动化学院,北京 100081)
0 引 言
随着移动终端与移动互联网业务在国内的普及,越来越多的个性化需求应运而生,其中室内定位的需求越来越强烈[1,2]。为实现高精度室内定位,Xu Y等人[3]利用卡尔曼滤波(Kalman filtering,KF)结合了超带宽(ultra wideband,UWB)与惯性测量单元(inertial measurement unit,IMU),实现了室内环境下的高精度定位。Xu Y等人[4]进一步采用联邦卡尔曼滤波进行融合定位,使得定位系统精度进一步提升。Shi Q等人[5]在定位过程中引入了回环检测,抑制了组合定位系统静止时的漂移问题。
目前,基于KF的组合定位算法已具有较高的精度,但在复杂室内环境下,UWB传感器易受复杂室内环境的干扰且IMU存在误差累积,导致观测量上存在较大的非高斯噪声[6~9]。采用KF作为框架的融合定位算法难以处理观测量上的非高斯噪声,导致定位精度严重下降[10]。近年来,Chen B等人[7]提出了最大相关熵卡尔曼滤波(maximum correntropy Kalman filtering,MCKF)算法,可有效处理观测量上的非高斯噪声。但MCKF在噪声类型不单一时,滤波精度以及鲁棒性会大幅下降,难以应用于噪声类型多变的室内定位系统。
本文针对MCKF存在的上述问题进行了改进,提出了改进最大相关熵卡尔曼滤波(improved MCKF,I-MCKF),利用新息对MCKF的观测噪声协方差矩阵进行先验修正,提高了MCKF在噪声类型不单一时的滤波精度及鲁棒性。将I-MKCF应用于室内组合定位系统中,提出了基于I-MCKF的UWB/IMU室内组合定位算法。并在实际室内环境下,进行动态实验,以验证基于I-MCKF的UWB与IMU的组合定位算法的精度与可行性。
1 基于UWB与IMU的定位算法
1.1 基于飞行时间定位算法
UWB定位坐标利用基于飞行时间(time of flight,TOF)定位算法进行解算。TOF定位算法利用双面双向测距法测量标签到各个基站的距离[11],使用三角定位法计算出标签的坐标[6]。r1,r2,r3为测量出的标签与基站的距离,基站坐标已知,其横坐标分别为xA,xB,xC,纵坐标分别为yA,yB,yC,则标签xD,yD的坐标可通过解方程组(1)得到,将第k次采样获得的标签坐标记为(xUWB(k),yUWB(k))
(1)
1.2 惯导解算
将IMU载体静置,参数初始化后根据测得的加速度、角速度与姿态矩阵即可计算出速度[7],进而计算出第k次采样时IMU定位坐标(xIMU(k),yIMU(k))。
虽然利用上述定位方法获得的(xUWB(k),yUWB(k))与(xIMU(k),yIMU(k))通过卡尔曼滤波即可得到传感器融合定位后的坐标。但在实际应用中,由于UWB易受复杂室内环境的影响以及IMU受误差累积等影响,卡尔曼滤波难以对噪声准确建模,使得系统的定位精度大幅下降。采用MCKF算法对测量出的坐标进行滤波处理可一定程度降低上述噪声对定位精度的影响,提升定位精度。
2 MCKF
MCKF将最大熵准则与卡尔曼滤波结合,具有更高的鲁棒性,可较好地处理观测量上的非高斯噪声[12]。MCKF在传感器的每一次采样后利用不动点迭代至最大熵点,其具体计算过程如下所示:
1)确定最大熵的核函数Gσ以及核函数带宽σ,通常核函数选为高斯核函数。同时设定初始状态估计值(0|0)以及初始误差协方差矩阵P(0|0),取采样次数k=1。
2)更新估计状态以及误差协方差矩阵,并对先验误差协方差矩阵P(k|k-1)与过程噪声协方差矩阵R(k)进行Cholesky分解得到Bp(k|k-1)与Br(k),取迭代次数t=1,并且取(k|k)0=(k|k-1)。根据系统模型,构造相关熵模型的先验值D(k)、后验值W(k)以及D(k)与W(k)(k|k)的残差E(k),需计算D(k)与W(k)(k|k)相关熵最大时的(k|k)t。
3)使用不动点迭代算法,根据式(2)~式(8)计算出相关熵最大时的(k|k)t,不动点迭代算法如下所示
(2)
(3)
(4)
(5)
(6)
(7)
H(k)(k|k-1)]
(8)

4)当第t次迭代后(k|k)t的变化小于误差限ε,则停止迭代并输出(k|k)t,否则重复步骤(3)。
5)更新误差协方差矩阵
P(k)=[I-(k)H(k)]P(k|k-1)[I-(k)H(k)]T
(9)
3 基于I-MCKF的组合定位算法
3.1 I-MCKF
本文提出了I-MCKF,利用新息对观测噪声协方差矩阵进行动态修正,从而提升MCKF在噪声类型不单一时的滤波精度。
I-MCKF在MCKF的步骤(2)后加入观测噪声协方差矩阵修正环节。首先计算新息z(k)及其协方差估计值(k),通常取遗忘因子λ=0.95,则
z(k)=y(k)-H(k)X(k|k-1)
(10)
(11)
(12)
但当噪声类型不单一时,单一估值的观测噪声协方差矩阵R(k)并不能使式(12)成立,故须校正R(k),使其满足式(12)。校正R(k)时,首先构造中间变量N(k)
N(k)=(k)-H(k)P(k|k-1)HT(k)
(13)
(14)
β1|kβ2|kr21β2|kr22…β2|kβn|kr2n
⋮⋮⋮
β1|kβn|krn1β2|kβn|krn2…βn|krnm)
(15)
式中nij与rij分别为矩阵N(k)与(k)的第i行第j列元素。将式(10)~式(15)插入式(3)、式(4)之间,即可代到I-MCKF。I-MCKF将修正后的(k)用于MCKF的剩余步骤,即可提升MCKF的滤波精度,保证其在噪声类型不单一时的性能。
3.2 基于I-MCKF室内组合定位算法


(16)
(17)
式中μ为过程噪声,η为观测噪声。
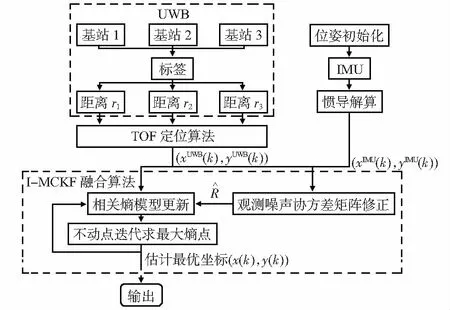
图1 基于I-MCKF的组合定位算法
建立状态方程与观测方程后,对噪声协方差矩阵初始化,保证在使用最大熵原理进行定点迭代时可以收敛,并加快定点迭代的收敛速度。噪声协方差矩阵的值可利用经验进行估计,也可通过实验测量得出。
根据计算出的噪声协方差矩阵构造相关熵模型为

(18)
D(k)=B(k)-1[(k|k-1)Y(k)]
(19)
(20)
式中Y(k)为第k次采样时的采样值,chol(x)为Cholesky算子,表示对x进行Cholesky分解。将式(16)~式(20)代入I-MKCF算法中,利用不动点迭代算法计算出熵最大时标签坐标的估计值(x(k),y(k)),即融合定位结果。
4 室内动态定位实验与结果分析
本文的实验场景设计如图2所示,其中三个基站的坐标分别为(0,0),(4.45,7.40),(8.90,0),运动轨迹选择绕室内行进一周。
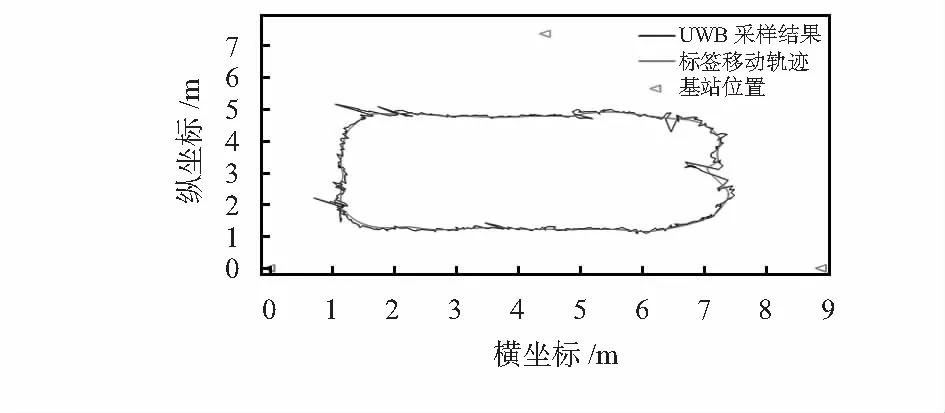
图2 实验场景示意
初始化IMU参数后,手持标签沿着上述路径移动,并将无KF组合定位算法、MCKF组合定位算法与I-MCKF组合定位算法的输出进行对比,结果如图3、图4以及表1所示。
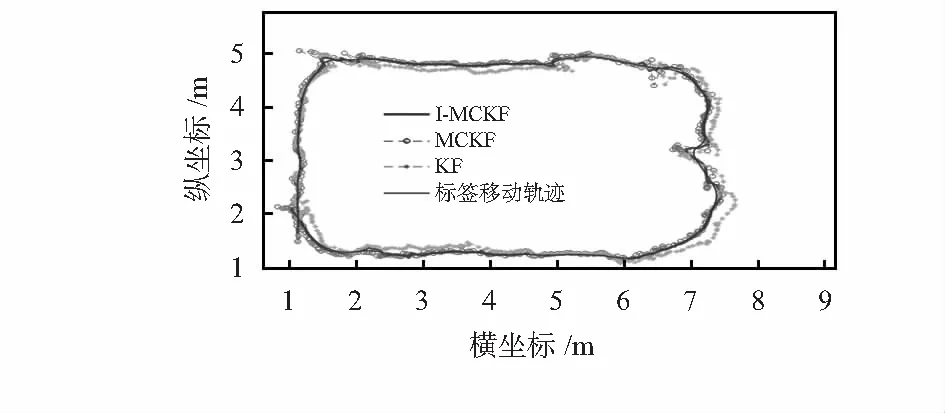
图3 三种组合定位算法定位结果
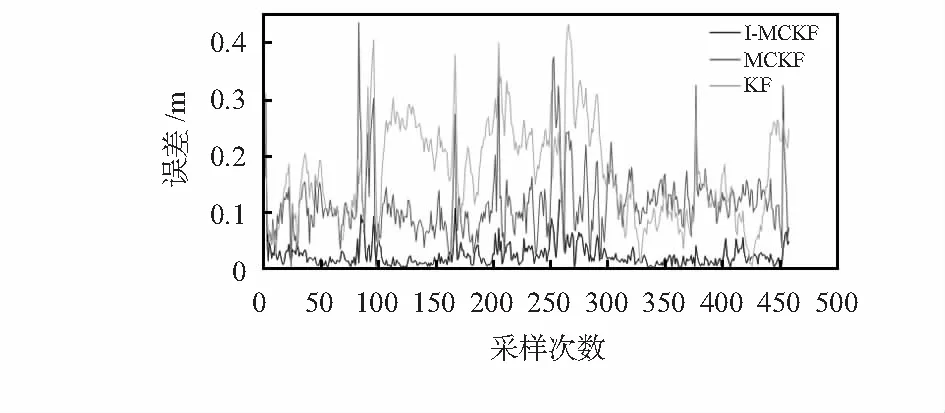
图4 三种定位算法误差对比结果
实验结果表明:KF组合定位算法的均方根误差(root mean square error,RMSE)最大,为0.091 m,最大误差为0.433 m;MCKF组合定位算法的RMSE为0.062 m,相较于KF组合定位算法降低了31.9 %;I-MCKF组合定位算法的RMSE为0.023 m,相较于MCKF组合定位算法进一步降低了62.9 %。

表1 三种定位方法在室内环境下的误差
5 结 论
实验结果表明:KF组合定位算法受复杂室内环境的干扰以及误差累积的影响较大,故定位精度较低。MCKF虽然可以一定程度上抑制复杂室内环境的干扰以及误差累积的影响,但由于室内环境中观测噪声多变,使得MCKF的滤波精度降低。I-MCKF通过对MCKF的观测噪声协方差矩阵进行实时修正,显著提升了MCKF在噪声类型不单一时的性能,故I-MCKF组合定位算法具有最高的定位精度,可实现高精度室内定位。此外,I-MCKF组合定位算法的更新频率可达100 Hz,满足室内定位系统实时定位需求。

