基于CEEMDAN-LSSVM-ARIMA模型的短期光伏功率预测*

王 瑞， 高 强， 逯 静

(1.河南理工大学 电气工程与自动化学院,河南 焦作 454000；2.河南理工大学 计算机科学与技术学院,河南 焦作 454000)

0 引 言

随着光伏发电的迅速发展,大规模的光伏并网对电力系统的冲击越来越明显,准确的短期光伏功率预测,能够有效地缓解光伏并网对电力系统造成的压力,对确保电网稳定运行和资源合理分配有重要的意义[1,2]。

目前,人们通常分析光伏发电功率数据历史规律与外部影响因素之间的关联,建立预测模型,对短期光伏功率进行预测[3～14]。文献[6]利用智能优化算法改进最小二乘支持向量机(least squares support vector machine,LSSVM),优化了光伏功率预测效果,但忽略了输入特征对预测效果的影响。文献[4,7]利用差分自回归移动平均(autoregressive integrated moving average,ARIMA)模型分别进行光伏功率与风功率预测，ARIMA模型表现出优越的时间序列预测性能。文献[8,9]分别采用小波包和经验模态分解(empirical mode decomposition,EMD)将光伏功率序列分解,降低光伏功率序列的非平稳特征。EMD克服了小波分解需预先人为经验选择基函数与分解层数的缺陷,但分解过程存在模态混叠现象。集成经验模态分解(EEMD)、完备集成经验模态分解(CEEMD)和CEEMDAN为EMD的改进方法,采用不同的方式消除模态混叠现象,其中CEEMDAN表现出良好的性能,被广泛应用于多个领域[10～12]。一些学者在预测过程中引入误差修正机制,有效地提升了光伏功率的预测精度[13,14]。

本文提出一种基于CEEMDAN-LSSVM-ARIMA模型的短期光伏功率预测方法。通过CEEMDAN将光伏功率序列分解成相对平稳的不同子序列;考虑到子序列频率特征变化对模型输入特征的影响,利用增量搜索法改进LSSVM，增加其自适应选择适合输入特征的能力,对各子序列分别建立改进LSSVM预测模型，求和重构各子序列预测结果得初步预测值；分析误差序列特征,发现误差序列的变化呈现一定的规律,视误差序列为时间序列,建立ARIMA误差修正模型,将误差预测值与初步预测值叠加得到最终预测结果。

1 光伏功率CEEMDAN原理与方法

CEEMDAN在EMD的基础上,通过自适应添加高斯白噪声,克服了模态混叠现象,有效地分解非平稳的序列。采用CEEMDAN分解光伏功率序列的具体步骤如下：

设Y为历史光伏功率序列，Ej(*)为经EMD产生的第j阶模态分量算子，ωn(t)为第n次添加的高斯白噪声序列，IMFk为经CEEMDAN得到的第k阶本征模态分量序列，δk-1为求解IMFk的自适应系数。

1)向原始序列Y中添加自适应高斯白噪声δ0ωn(t)，n=1,2,…,N为添加的次数，即

Yn=Y+δ0ωn(t)

(1)

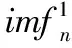
(2)

r1=Y-IMF1

(3)

2)向余量序列r1中添加自适应高斯白噪声δ1E1(ωn(t))，n=1,2,…,N,即

r1n=r1+δ1E1(ωn(t))

(4)

对r1n分别进行EMD分解，则CEEMDAN分解的二阶本征模态分量序列IMF2为

(5)

3)对k=2,3,…，K,重复步骤(2)，得到第k+1阶本征模态分量序列和第k个残余分量序列,即

(6)

rk=rk-1-IMFk

(7)

4)直到残余分量序列的极值点个数不超过2个为止，最终残余分量序列R为

(8)

历史光伏功率序列Y经CEEMDAN分解成K个本征模态分量序列IMFk和一个残余分量序列R,共K+1个子序列。

2 光伏功率LSSVM模型原理与改进

2.1 LSSVM模型原理

LSSVM遵循结构风险最小化原则,在SVM的基础上,将损失函数构造成最小二乘函数,不等式约束转成等式约束,进而将二次规划问题的求解转换成了求解线性方程组。LSSVM目标优化函数为

s.t.yi=ωTφ(xi)+b+ξi,i=1,2,…,n

(9)

式中c为正则化参数;ξi为误差变量;ω为法向量;b为偏置量。

引入拉格朗日算子,根据KKT条件和Mercer条件,最终得到的回归函数为

(10)

式中k(xi,xj)为核函数，通常采用径向基核函数，根据式(10)进行回归预测。

2.2 改进LSSVM的光伏功率预测

客观自适应选择适合的输入特征,是确保LSSVM预测效果的关键。文中考虑的影响因素包括太阳直射辐照度、散射辐照度、总辐射辐照度、气温、板温、温差、湿度和气压，8个特征，可能的组合数为(2m-1),m=8,即255个,因此通过遍历所有的组合选择适合的输入特征是不可取的。

增量搜索法[15]的核心思想是,从剩余的特征中每次选择一个特征,添加到现有的输入特征中,使其目标变量相比上一次变化最多。由增量搜索法获得适合的输入特征,最多只需筛查m(m+1)/2,m=8,即36个组合。

因此，文中以训练误差为目标变量,采用增量搜索法改进LSSVM,使其自适应选择适合的输入特征。改进LSSVM自适应选择适合输入特征,进行光伏功率预测的步骤如下：

1)设初始输入特征集D为空集，初始训练误差e为0；

2)将原始特征集Sm=(x1,x2,…,xm)中每个特征按顺序保留在D中，得候选特征集D1,D2,…,Dm；

3)将对应Dm的样本数据输入到LSSVM中，由粒子群优化(particle swarm optimization,PSO)算法优化正则化参数和核函数参数,并行法[16]得训练误差e1,e2,…,em;

4)将对应min{e1,e2,…,em}的特征保存在D中,保存e=min{e1,e2,…,em};

5)对剩余特征P={Sm-D}执行步骤(2)和步骤(3)，由式(11)保存对应特征到D中，对应误差赋值给e

(11)

式中ea为候选特征集训练误差，τ>0为终止条件,文中设定τ=e/10;

6)继续对P={Sm-D}执行步骤(5),直到式(11)不成立或Sm为空集;

7)获得模型的适合输入特征D，输入预测样本数据，进行光伏功率预测。

3 ARIMA预测误差修正

由于分解模型和预测模型的自身限制,由初步预测结果和实际值构造误差序列,分析发现其变化呈现一定的规律[17]。将误差序列视为随机时间序列,利用ARIMA模型进行误差修正，ARIMA模型可表示为

(12)

式中L为滞后算子,d为差分阶数,φi为自适应系数,θi为移动平均系数,p为自回归阶数,q为移动平均阶数,εt为残差序列。

建立ARIMA误差修正模型的步骤如下[7]：1)由ADF单根检验误差序列是否平稳，若不平稳，对误差序列d次差分后继续检验，确定差分阶数d；2)根据误差序列自相关和偏自相关,由赤池信息准则(Akaike information criterion,AIC)选择p和q的阶数,以AIC值最小确定p和q；3)利用最小二乘法估计模型的参数，通过参数显著性检验和残差白噪声检验判断、选定参数;4)建立ARIMA误差修正模型并预测。

4 短期光伏功率预测建模

提出基于CEEMDAN-LSSVM-ARIMA模型的短期光伏功率预测方法,预测未来1 h(4个节点)光伏发电功率。光伏功率预测模型如图1。

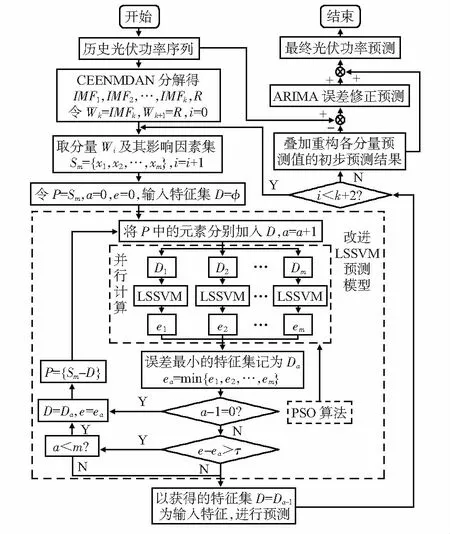
图1 光伏功率预测模型

光伏功率预测模型的步骤如下：

1) 获取目标光伏电站实际数据,取采样点前后3～6个时间节点的平均值补全缺失数据。记Y为历史光伏功率序列,由CEEMDAN将Y分解为K+1个子序列,分别记为W1，W2，…,Wk+1,其中,前K个为本征模态序列IMFk,第K+1个为残余序列R。

2)对各子序列分别建立改进LSSVM模型,并输入影响因素；预测模型自适应选择适合的输入影响因素特征进行预测,各子序列预测结果为u1,u2,…,uk,uk+1。

3)由式(13)对各子序列预测结果求和重构，得光伏功率初步预测结果Y′,由式(14)得到误差时间序列e

(13)

e=Y-Y′

(14)

4)分析误差特性,建立ARIMA误差修正模型,输入误差数据序列e,进行训练和预测,误差预测结果为e′。

5)叠加初步预测结果和误差预测结果得最终光伏功率预测结果

(15)

6)预测结果评价,文中采用平均绝对误差(MAE)和均方根误差(RMSE)衡量模型的预测性能,其值越小,模型性能越好

(16)

(17)

式中n为预测总数;Yi为第i个节点实际光伏发电功率值,i为第i个节点预测光伏发电功率值。

5 算例分析

从江苏某地区光伏电站2015—2016年实测数据中,多次随机按顺序选100天数据进行仿真实验,从中随机选一组(2016年5月23日～8月30日)对最后5天(8月26日～30日)的光伏功率进行预测分析。总装机容量为100 MW,数据采样周期为15 min,时间为每天06︰00—18︰00。光伏功率序列和经CEEMDAN分解序列分别如图2和图3。由图2和图3可看出，光伏功率序列具有非平稳性，被CEEMDAN分解成11个子序列，IMF1～10为本征模态子序列,R为剩余子序列,降低了非平稳性的影响。

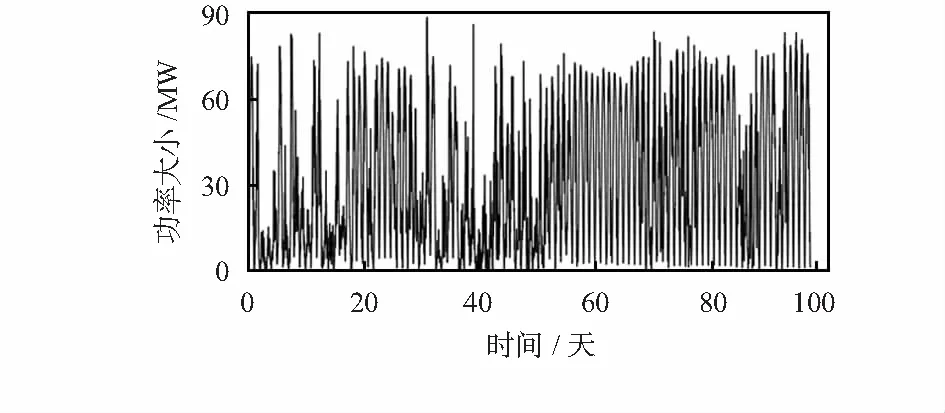
图2 光伏功率序列

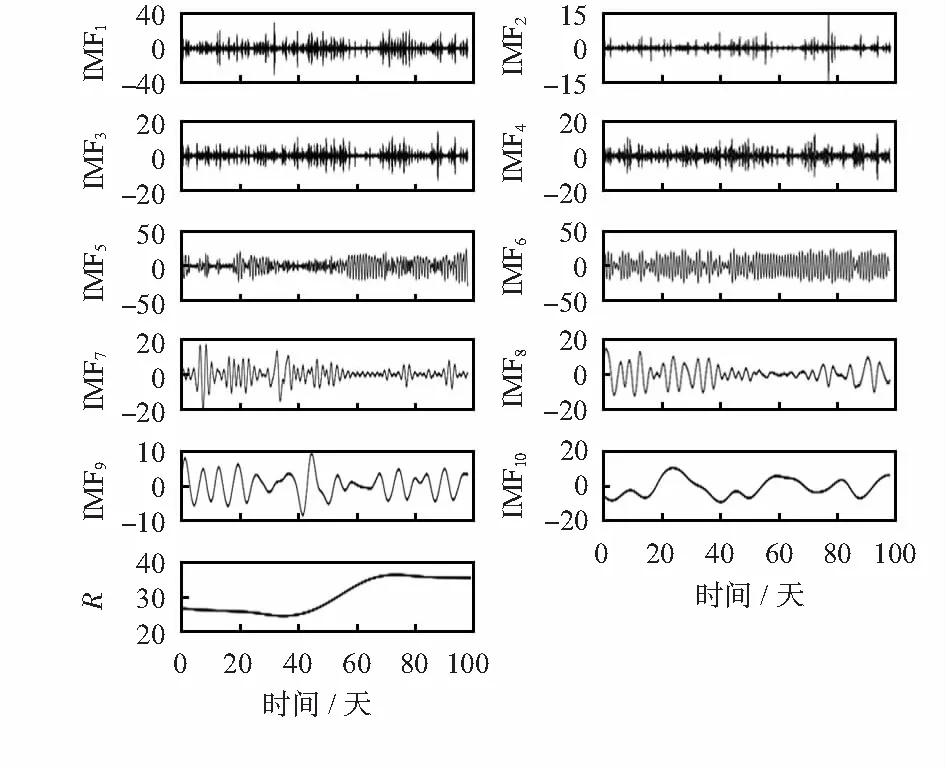
图3 光伏功率分解序列

对子序列分别建立改进LSSVM预测模型, 模型根据输入的子序列数据和影响因素特征数据,自适应选择适合的输入影响因素特征进行子序列预测；为弱化偶然性的影响，连续运行20次取平均值作为预测结果。PSO算法中,进化次数N=200,种群规模M=20,学习因子c1=1.5,c2=1.7,惯性权重w=0.5。

求和重构子序列预测结果得光伏功率初步预测结果,由初步预测结果和功率实际值构造误差时间序列,并进行分析,误差时间序列和误差的自相关和偏自相关如图4,图5所示。

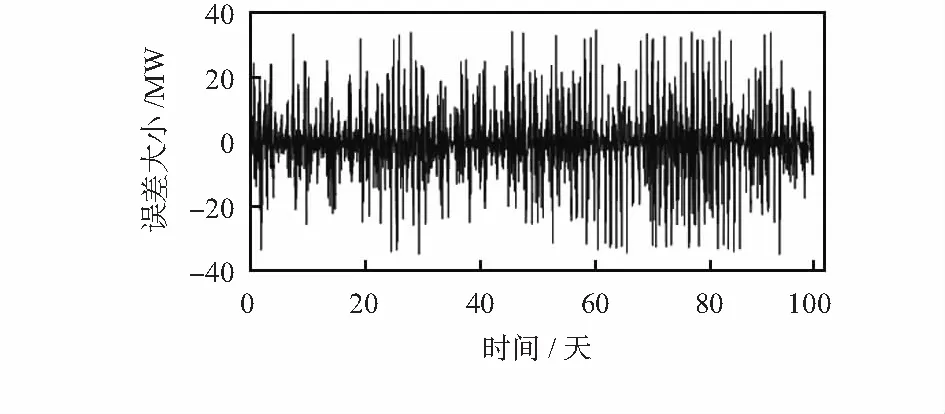
图4 误差序列

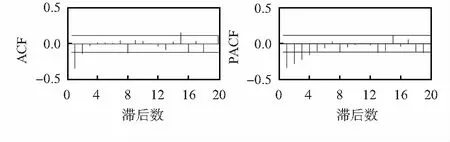
图5 误差的自相关和偏自相关

由图4，图5可看出,误差时间序列的变化呈现一定规律,存在一定程度的自相关和偏自相关。为进一步提高预测精度,采用 ARIMA模型对误差进行修正预测,经多次实验分析,设定差分次数、自回归和移动平均阶数上限dmax=5,pmax=8,qmax=8,具体参数组合根据ADF单根检验和由AIC准则自适应选定。连续5天的误差预测结果如图6所示,从图中可看出，通过ARIMA模型能够有效地进行误差修正预测。将误差预测结果与初步预测结果叠加，以修正初步预测结果得到最终的预测结果，提升模型的预测精度。

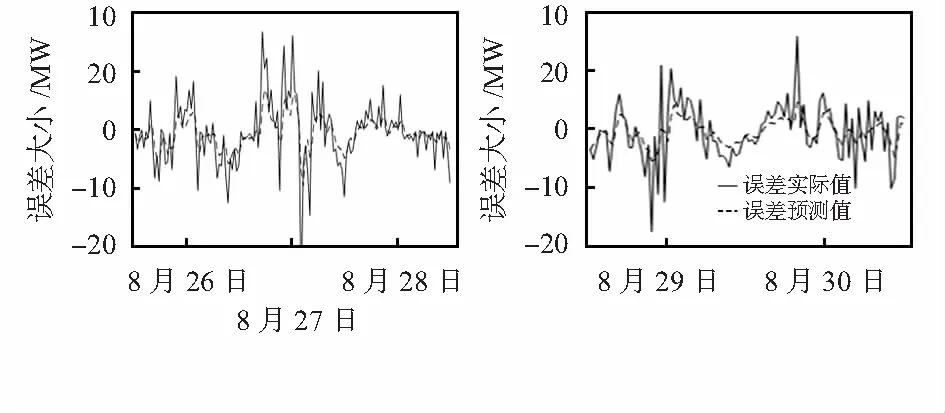
图6 误差修正预测结果

记P为皮尔森相关性分析,分别建立CEEMDAN-P-BP模型(方法一),CEEMDAN-P-LSSVM模型(方法二),CEEMDAN—改进LSSVM模型(方法三)和CEEMDAN—改进LSSVM-ARIMA模型(本文方法)对8月26～30日连续5天的光伏功率进行预测。其中，BP，LSSVM中的重要参数均采用PSO进行寻优。各方法预测结果曲线如图7所示,各方法预测误差如表1所示。

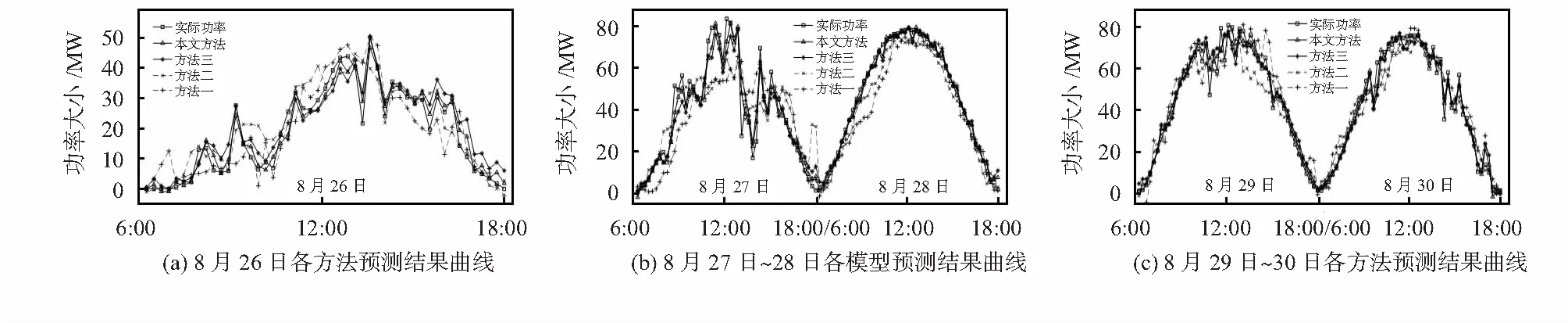
图7 8月26～30日各种方法预测结果

分析图7中预测结果,可得出,方法一和方法二在一定程度上能够预测出功率的整体趋势,但预测结果曲线与实际曲线拟合度差,局部偏差较大；方法三和本文方法因其采用的改进LSSVM模型能够自适应选择输入特征进行预测,预测结果与实际值拟合度高,波动性小,曲线相似度高,表明改进LSSVM模型的性能优于传统的LSSVM模型。

在图7(b)光伏功率由较大波动序列(8月27日)转换为较稳定序列(8月28日)，及图7(c)光伏功率稳定序列的局部突变情况下,方法一和方法二的预测结果都出现了局部明显的偏离；方法三和本文方法预测结果仅有短暂轻微的波动,仍能较好地预测光伏功率的变化趋势,表现出较好的预测效果。

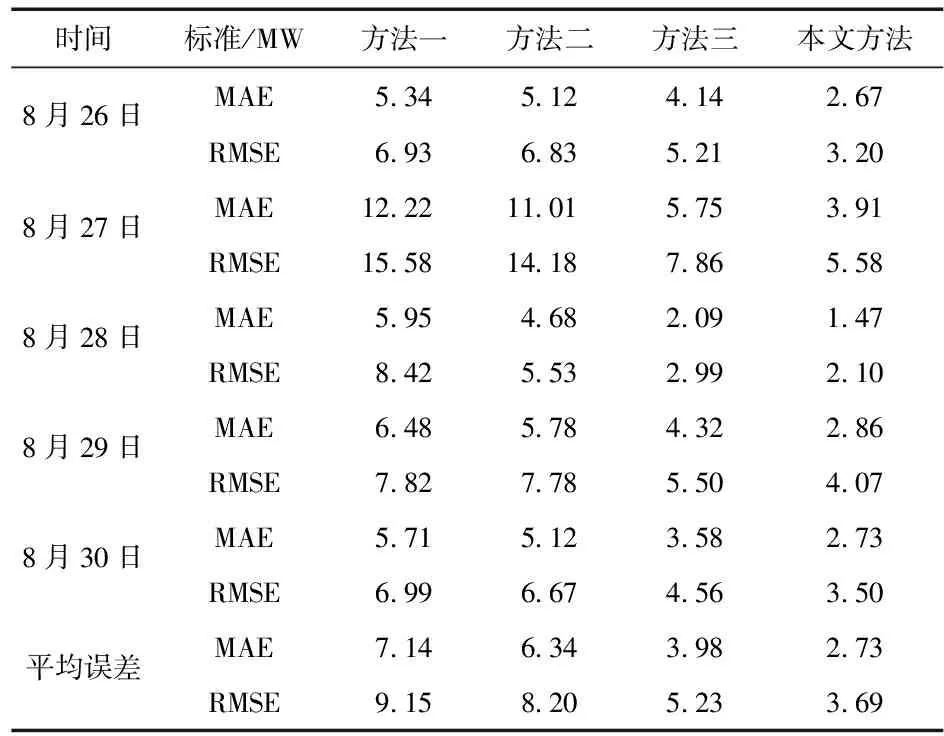
表1 各中方法预测误差

结合图7和表1,分析得出,本文方法和方法三在整体上都能较好地预测短期光伏功率的变化趋势,预测误差较小；方法三的预测平均误差MAE值为3.98 MW，RMSE值为5.23 MW，明显低于方法一和方法二；由于利用ARIMA模型进行误差修正补偿,本文方法预测误差进一步降低，预测平均误差MAE值为2.73 MW，RMSE值为3.69 MW；在光伏功率波动程度相似(8月29日～30日)情况下,本文方法预测误差基本保持稳定，验证了本文方法的有效性。

6 结 论

1) 光伏功率序列经CEEMDAN分解为不同频率的子序列能够降低光伏功率的复杂度,有利于功率特性分析和建模预测。2) 改进的LSSVM模型加强了自适应选择适合输入特征的能力,其性能优于传统的LSSVM,能提升光伏功率预测精度。3) 分析光伏功率预测误差序列特性,发现误差变化存在一定的规律,ARIMA模型能够有效的修正误差,进一步提高光伏功率的预测精度。

光伏功率的分解子序列具有不同的特征变化,对其更高性能的预测方式还需深入研究，同时可以分析误差序列特征,通过误差修正进一步提高预测精度，今后将从这两方面进一步对光伏功率预测进行研究。