改进粒子滤波的无人机航迹预测方法*

曾 润， 田 杰， 江 虹， 王智宁

(1.西南科技大学 信息工程学院，四川 绵阳 621010；2.中国工程物理研究院 电子工程研究所，四川 绵阳 621900)

0 引 言

随着无人机(unmanned aerial vehicle,UAV)技术与应用的快速发展，无人机正成为很多场景执行任务的最佳选择[1,2]。对无人机航迹的准确预测是保障无人机安全、有效飞行的重要基础，无人机航迹预测在无人机跟踪[3]、事故预警[4]、航迹规划[5]等方面发挥着重要的作用。

模型滤波是无人机航迹预测的重要方法。文献[6]指出，在现有状态估计算法中，粒子滤波(particle filtering,PF)算法是基于递推贝叶斯(Bayes)滤波估计的一种近似最优估计方法，更适用于无人机这类具有非线性运动特征的系统模型。如文献[7]基于粒子滤波通过对无人机的俯仰角、横滚角、偏航角的预测间接实现对无人机的航迹预测；文献[8]提出一种结合粒子滤波与长短期记忆(long short-term memory,LSTM)网络的AGV(automated guided vehicle)位置持续估计算法。但传统粒子滤波算法存在权值退化、样本贫化等问题[9]。为此文献[10]使用无迹卡尔曼滤波(unscented Kalman filtering,UKF)产生建议密度函数，提出一种改进的无迹卡尔曼粒子滤波(unscented Kalman particle filtering)算法，一定程度上提高了预测精度。但由于UKF算法的无迹变换(unscented transform,UT)需要对协方差矩阵做Cholesky分解，这要求矩阵必须是正定的，对于无人机这类多维状态模型在矩阵计算中很有可能迭代为非正定，导致算法在运行过程中极易崩溃。文献[11]将粒子滤波与神经网络相结合，一定程度上增加了粒子的多样性。但算法复杂度太高达不到实时性要求，不适用于无人机航迹预测。

针对以上问题，本文基于扩展卡尔曼滤波(extended Kalman filtering,EKF)结合权重优化思想[12]与数据融合思想，提出一种基于数据融合的扩展粒子滤波(data-fusioned extended particle filtering,DFEPF)算法，建立航迹预测模型，并仿真对比三种常用非线性滤波方法，验证本文改进方法对无人机航迹预测的有效性。

1 航迹预测系统模型

获取到每个观测站传感器的预测结果后，本文使用标准线性最小方差加权融合规则来计算最佳融合估计值，如式(1)所示

(1)

式中ai为权重系数，计算公式为式(2)

(2)

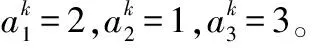
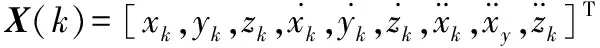
X(k+1)=φX(k)+w(k)

(3)

其中，φ为状态转移矩阵。假设观测站SN的坐标位置为(xN,yN,zN)，则可得到该观测站相对于无人机的距离dN和该观测站相对于无人机的俯仰角α与横向角β，建立系统观测方程

Z(k)=h(X(k))+v(k)

(4)

h(X(k))=

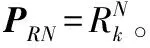
2 改进粒子滤波算法分析

2.1 改进粒子滤波算法原理

粒子滤波是非线性递推Bayes估计问题的一种实现方法，其存在严重的粒子退化问题，若干次迭代之后大部分粒子的权值小到可忽略不计，使权重更新失效。本文分别从推荐密度函数、重采样两个步骤对传统粒子滤波算法进行改进。

首先,在重要性采样阶段中采用EKF算法融合最新的观测值Zk为每个粒子计算其均值与协方差，通过以该均值与方差为参数的正态分布来近似建议密度函数，即式(5)。建议密度函数生成详细步骤见2.2节。式(5)如下

(5)

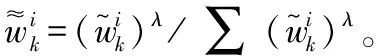
(6)

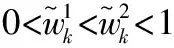
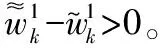
2.2 改进粒子滤波算法步骤

2)重要性采样：使用EKF算法计算粒子均值与协方差(包含预测步)：

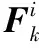
(7)

(8)

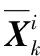
(9)

4)求粒子期望得到k时刻预测结果，返回步骤(2)直到完成所有迭代采样。

3 仿真分析

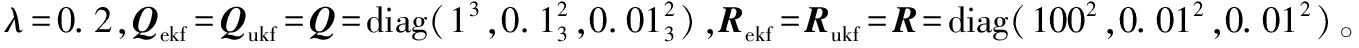
3.1 航迹预测性能分析

设粒子数N=200，观测站SA(100,200,0),SB(800,800,0),SC(100,900,0)。观测噪声协方差PR1=diag(1002,0.12,0.12)，PR2=diag(1102,0.12,0.12)，PR3=diag(1202,0.12,0.12)。由式(1)、式(2)得多观测站DFEPF算法的预测结果

(10)

采用式(11)所示均方根(root mean squre,RMS)误差衡量预测偏差。对比传统算法单观测站预测结果、每个采样点RMS偏差、无人机多个预测状态与真实值的偏差均值得到如图1～图3所示结果。式(11)如下

Xreal(2,i))2+(Xfilter(3,i)-Xreal(3,i))2)-1/2/M

(11)

图1 预测偏差(粒子数N=200)

图2 预测参数偏差对比(粒子数N=200)

图3 不同噪声方差预测误差对比

图4可看出，DFEPF相比其它算法能够更好地预测出无人机真实状态；由图1可看出，DFEPF相比其它算法每个采样点的预测偏差更小；由图2可看出，DFEPF算法比EKF、UKF、PF算法多个参数的预测偏差均值都要小。对比4种算法的不同滤波参数如表1所示。

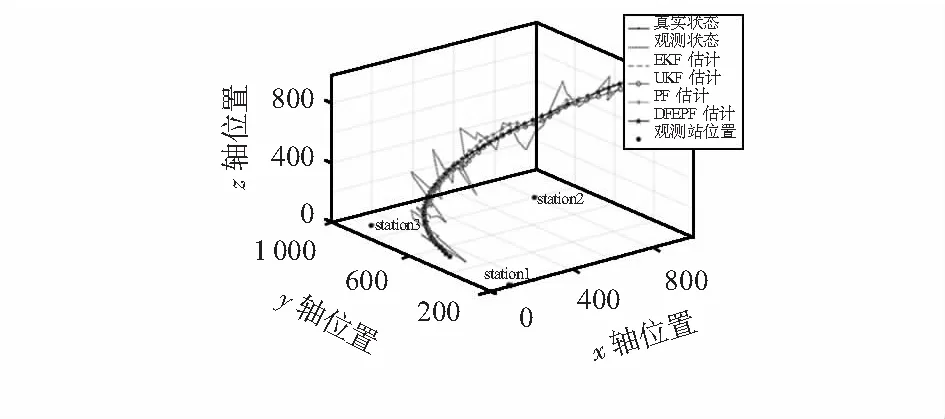
图4 多种算法预测结果对比(粒子数N=200)

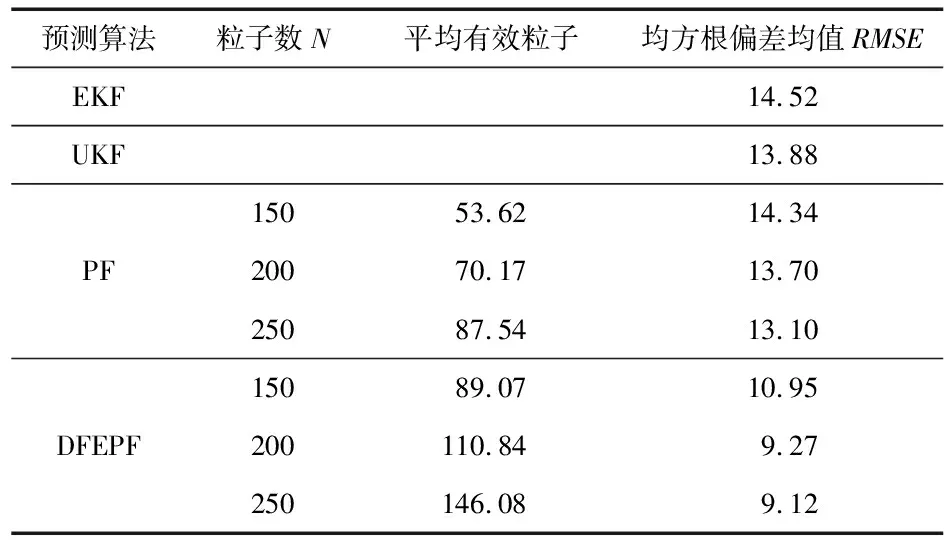
表1 多种算法不同滤波参数对比

从表1不难看出，通过EKF算法协助重要性采样，并引入权重漂移思想的DFEPF算法的有效粒子Neff数相比基本粒子滤波的有所提高，有效削弱了粒子退化，提高了预测精度。由仿真结果可粗略统计出：DFEPF算法比EKF、UKF、PF的均方根偏差均值整体上分别减小了48.46 %,41.92 %,40.22 %；平均有效粒子Neff相比基本粒子滤波算法增多63.72 %。

3.2 航迹预测算法稳定性与时间复杂度分析

设置不同的噪声方差Rc，粒子数N，将采样次数增大到M=400。计算RMS预测误差如图3所示。记录粒子数N=200时，各种滤波算法的单步预测时间如图5所示。

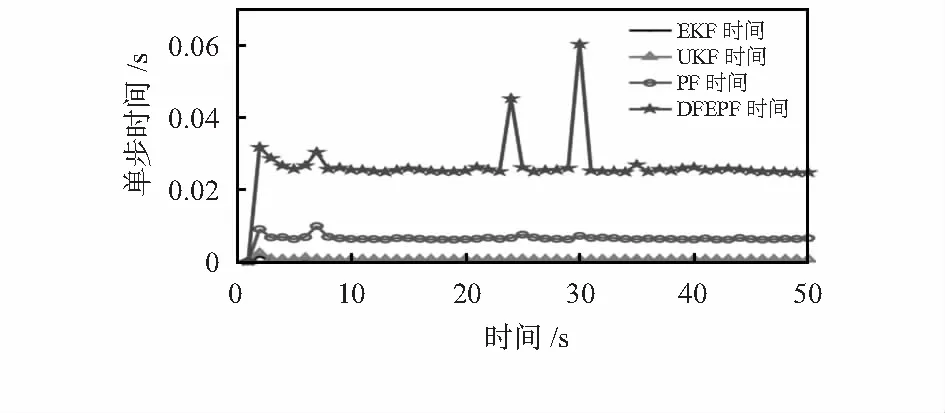
图5 单步预测时间对比

由图3可看出：当N=200，Rc=5R或Rc=8R时，当Rc=5R，N=200或N=400时，基本PF算法均会在不同的时间开始发散，而DFEPF算法始终处于收敛的状态。多次取不同噪声方差Rc与粒子数目N实验，总结出本文提出的DFEPF相比基本PF算法更加稳定；DFEPF算法由于涉及生成建议密度函数、重采样、数据融合等步骤，相比传统非线性滤波算法时间复杂度略高，但整体上仍可达到无人机状态监测的实时性要求[15]。

4 结 论

本文针对无人机非线性航迹难以预测的问题，提出数据融合的改进粒子滤波航迹预测方法。仿真试验表明：改进算法较EKF、UKF、PF算法的均方根偏差均值整体上分别减小48.46 %,41.92 %,40.22 %；平均有效粒子较基本PF算法增多63.72 %；较基本PF算法更加稳定；较传统非线性滤波算法更耗时，但能够满足航迹预测实时性要求，可为三维航迹预测研究提供参考。未来的工作将针对重采样与重要性采样等步骤进一步优化。