一类多重积分蒙特卡罗近似求解及其局部加权回归拟合

许昌林，舒洪铭

(1.北方民族大学 数学与信息科学学院，宁夏 银川 750021;2.北方民族大学 宁夏智能信息与大数据处理重点实验室，宁夏 银川 750021)

0 引言

对于多重积分的计算问题，若利用传统的将多重积分化为累次积分方法进行求解，则有时会受到如积分区域的形状、维数、被积函数的复杂程度等因素的影响，使多重积分求解变得复杂甚至无法得到解。为此，许多学者从概率论的角度出发，寻求多重积分的概率求解方法，如通过积分区域的投影、依概率收敛、控制收敛定理以及勒贝格积分控制收敛定理等方法进行多重积分的求解［1-4］。还有学者从数值计算的角度出发，通过随机模拟法寻求多重积分的近似求解，如随机均匀数法［5］、蒙特卡罗方法［6］、利用抽样技术改进重积分的蒙特卡罗计算［7］、平均值估计计算法［8］、数论网格法［9］等。

多重积分在社会各个领域有重要应用，如利用地震多重积分对储层位置和厚度进行识别与表示，从而对地震阻抗反演进行建模研究［10-11］，以反映地震剖面上的地质层位和构造特征;在计及光伏发电相关性的研究方面，利用多重积分法和Gram-Charlier 级数解决计及光伏出力相关性概率潮流的输入和输出变量之间非线性关系带来的计算复杂性［12］;在稠密稀疏N 体问题解析函数近似计算方面，利用多重积分表示粒子间相互作用径向分布函数的解析表达式，从而得到稀疏区域到稠密球域的分析解，以计算蛋白质的径向函数［13］;非线性弱奇异多重积分不等式中未知参数的估计和应用［14-15］。

本文中，首先，对文献［3］提出的闭区域上一类复杂n 重积分在n→∞时的极限问题，通过构造适当的概率分布，利用辛钦大数定律和依概率收敛理论，对该n 重积分的极限问题给出了新的证明方法和思路，并该证明方法简洁易懂;其次，利用随机变量函数的数学期望与重积分之间的关系，对n 重积分进行离散化处理，通过蒙特卡罗法对n 重积分进行模拟仿真，并在蒙特卡罗法近似计算结果的基础上利用局部加权回归法对计算结果进行拟合，利用R 软件给出计算过程的可视化，进行近似计算和曲线拟合;然后，结合模拟计算和文献［3-4］的结论对文献［3］给出的一种n 重积分极限中的参数取值范围进行修正，将文献［3-4］给出的固定区域［0，1］×［0，1］×…×［0，1］上的n 重积分极限的结论推广至一般区域［0，u］×［0，u］×…×［0，u］上，并利用本文所提出的证明方法对该结论进行了证明;最后，结合蒙特卡罗算法对一般区域［0，u］×［0，u］×…×［0，u］上n 重积分进行模拟计算，并利用局部加权回归法对其进行拟合，从而进一步验证推广结论的合理性。

1 基于概率分布的一类多重积分极限问题的求解

文献［3］应用依概率收敛和控制收敛定理及其相关结论，对式(1)的n 重积分的极限进行证明，证明过程复杂且抽象，不容易理解。本文中借助概率论中随机变量的概率分布，给出一种新的证明方法。

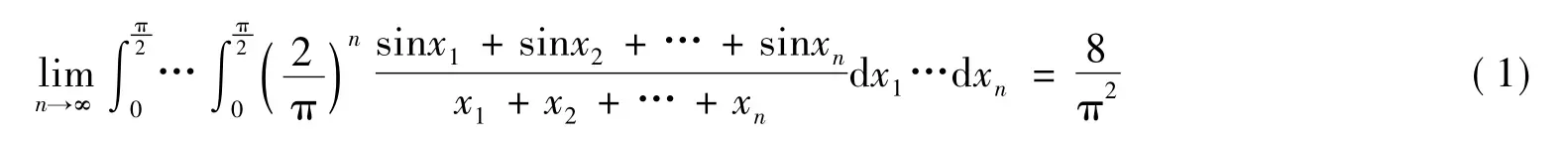
针对式(1)，下面给出具体证明过程。

为了证明和表示方便，令

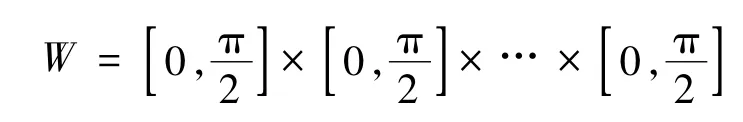
并将W 划分为

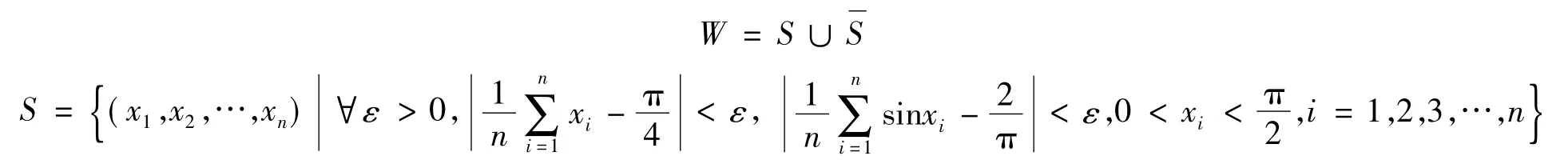
由于

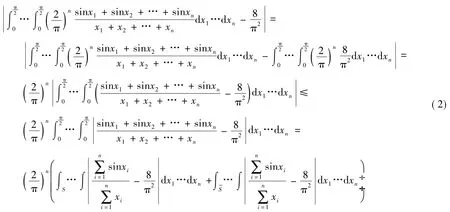
为了求解式(2)中的解，根据概率知识，假设连续性随机变量序列{Xi}(i=1，2，3，…，n)独立且同分布于上的均匀分布，则随机变量序列{Xi}的联合密度函数为:

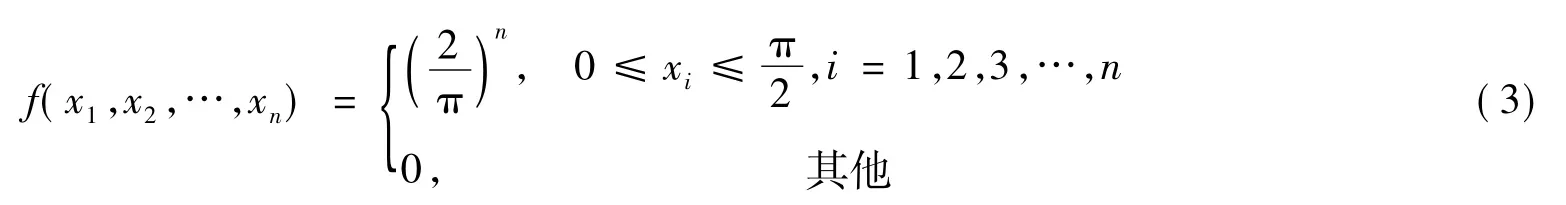
基于上述概率分布以及连续性随机变量在某区域上的概率与积分的关系，首先考虑式(2)在积分区域上的解。

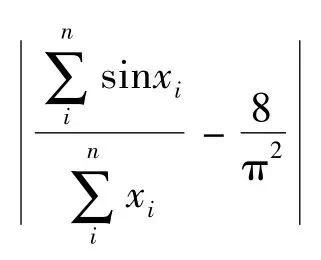
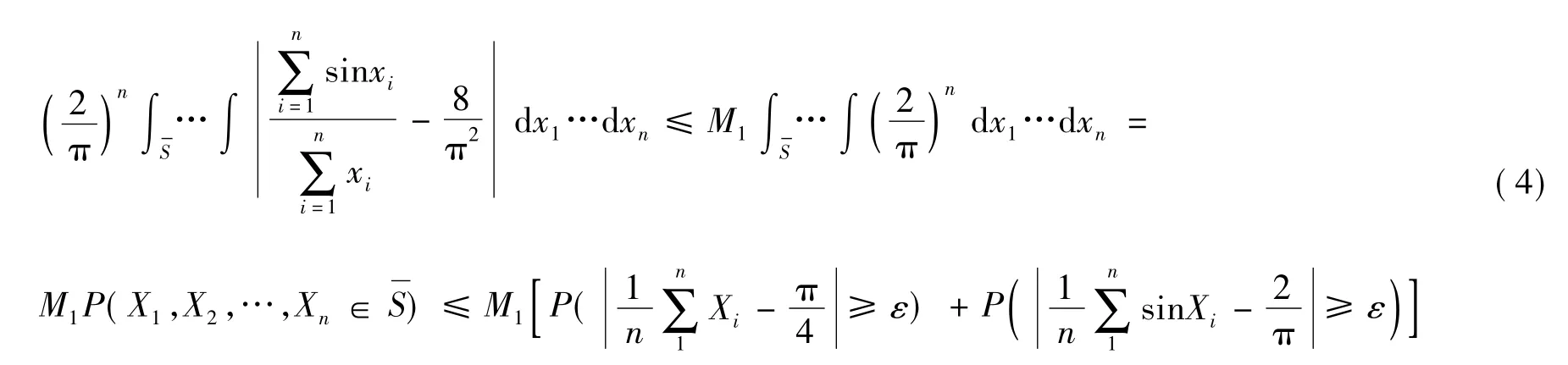
其次，考虑式(2)在区域S 上的积分情况。

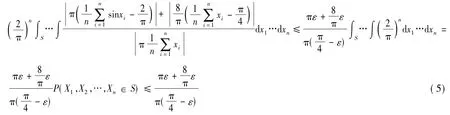
由式(4)和式(5)知:

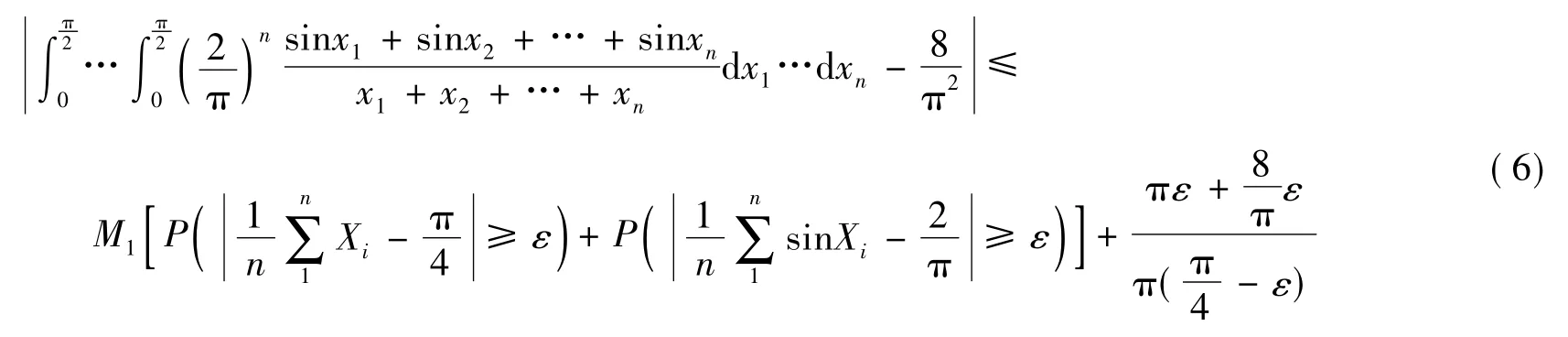
另外，由于随机变量Xi与sin Xi的期望存在，且分别为

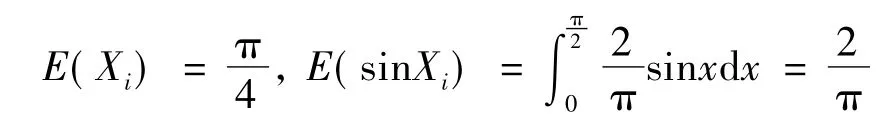
故由辛钦大数定律以及依概率收敛可知［16］，对任意ε＞0 有

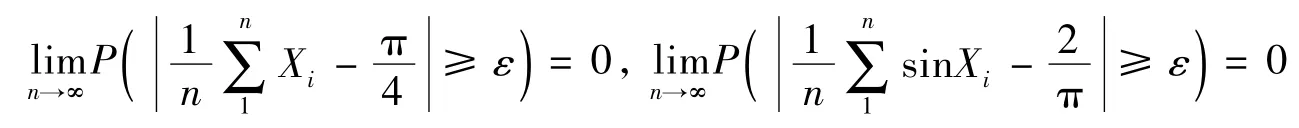
因此，对于式(6)由极限的夹迫性定理［17］可得

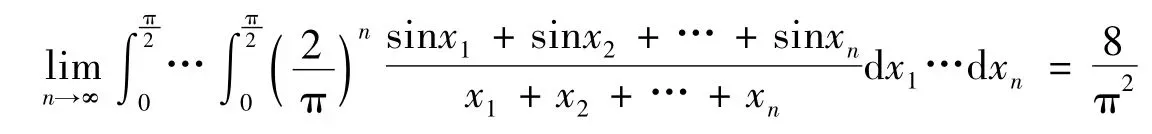
综上，式(1)得证。

2 一类多重积分近似求解的蒙特卡罗法及其局部加权回归拟合

2.1 n 重积分离散化

为了给出式(1)n 重积分在n→∞时的近似求解过程，首先基于多维连续性随机变量函数的数学期望与重积分之间的关系，将式(1)n 重积分离散化处理。由式(3)知，式(1)n 重积分表示为随机变量{Xi}(i=1，2，3，…，n)的函数的数学期望，即

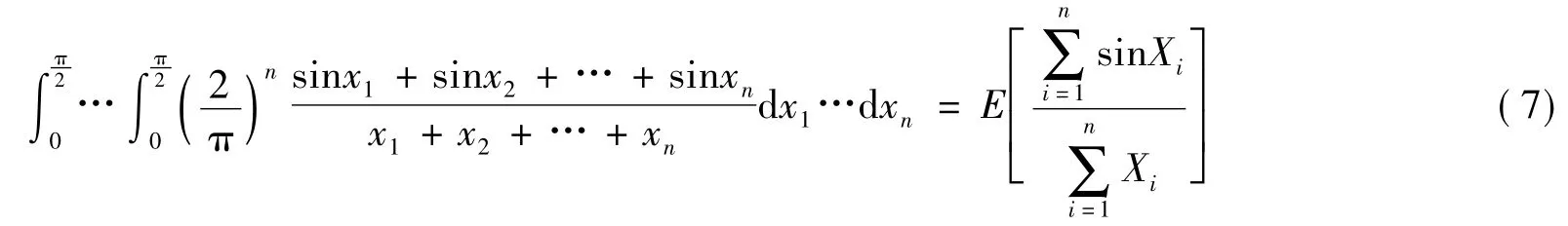
从而根据数学期望的性质，将式(7)进一步离散化为

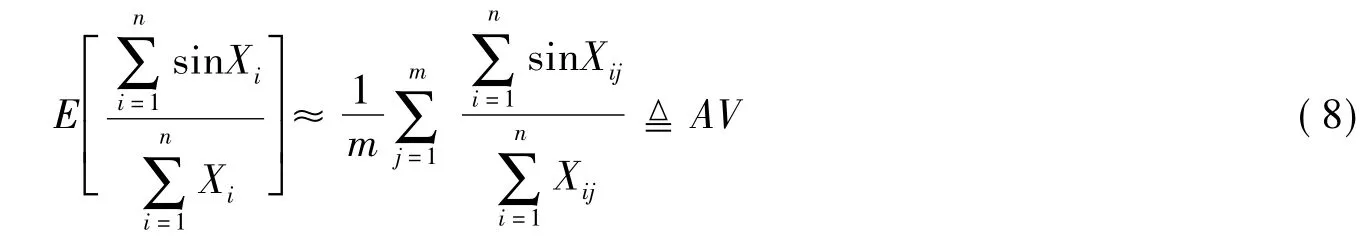
其中，式(8)右端随机变量{Xi}(i=1，2，3，…，n)独立同分布于上的离散均匀分布。

2.2 基于蒙特卡罗法的近似模拟算法

根据式(3)、式(7)和式(8)，得到计算式(1)n 重积分在n→∞时的蒙特卡罗算法，具体表述如算法1。

算法1:式(1)中n 重积分近似求解的蒙特卡罗算法

利用算法1，通过R 软件，对不同的m 值(m=2 000，m=5 000)，当n 重积分的重数n 从100 以步长100 增加至10 000 时，式(1)的n 重积分的近似值AV 与n→∞时极限值的仿真散点图如图1 所示。通过图1 可以发现，随着重积分重数n 的不断增大，近似值AV 越来越接近n→∞时的极限值LV，并在极限值LV 附近随机波动。由此可以看出，式(8)的离散化结果能更好地反映n 重积分当n→∞时的极限过程。

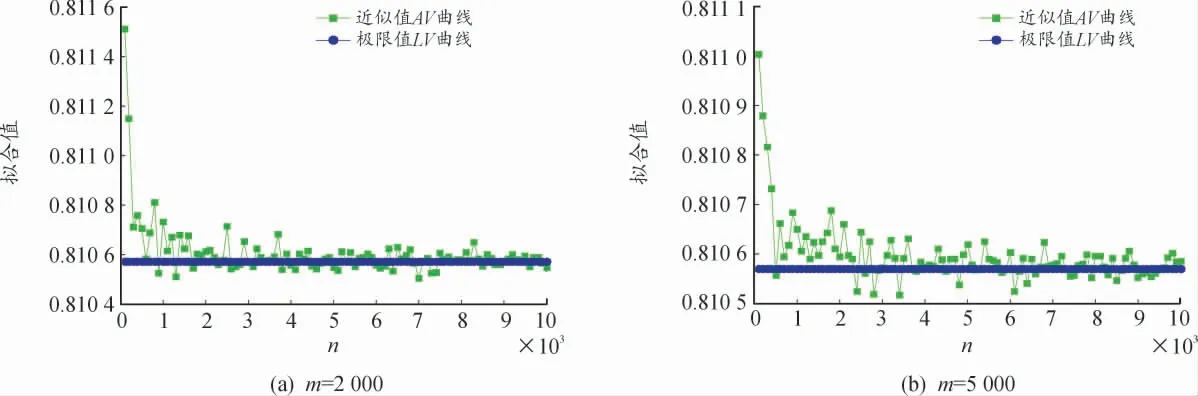
图1 不同m 值下式(1)n 重积分n 增加时AV 和LV 的变化趋势

2.3 基于局部加权回归的曲线拟合

图1 仿真结果是根据蒙特卡洛算法随机模拟计算得到。从图1 中可以看出，当重积分重数n 增加时，近似值AV 在其极限值LV 附近具有一定的波动性。为了能更好地反映式(1)的n 重积分当n→∞时的近似值AV 与其极限值LV 的逼近过程，在图1 相应条件下的散点图(数据)基础上，利用非参数回归的方法对其进行拟合。其中，局部加权回归(Lowess)是一种非参数回归方法［18-20］，能很好地处理这种问题，它主要是把样本划分成一个个小区间，并对区间中的样本进行多项式拟合，不断重复这个过程得到在不同区间的加权回归曲线，最后再把这些回归曲线的中心连在一起合成完整的回归曲线，具体过程如下:①决定拟合点的数量和位置;②以拟合点为中心，确定k 个最接近的点;③通过权重函数计算这k 个点的权重;④通过加权线性回归进行多项式拟合，确定k 个平滑点;⑤对所有拟合点重复以上步骤;⑥将所有平滑点连接起来得出拟合曲线。

基于上述Lowess 拟合过程，分别对图1 中m=2 000 和m=5 000 的条件下，重积分重数n 从100 以步长100 增加至10 000 时的随机模拟计算结果进一步进行Lowess 拟合，拟合结果如图2 所示。从图2可以看出，对于不同m 取值，当重积分重数n 不断增加时，Lowess 拟合曲线LWRV 逐步逼近重积分的极限值LV。由此看出，Lowess 拟合曲线能较好地反映出n 重积分收敛的可视化过程。

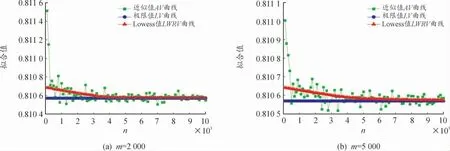
图2 不同m 值下(1)式n 重积分n 增加时AV、LV 与LWRV 的变化趋势

通过蒙特卡罗法和局部加权回归拟合对n 重积分的收敛过程进行可视化，一方面可以验证重积分的收敛性，另一方面可以利用蒙特卡罗法对复杂重积分进行近似求解，这为求解多重积分又提供了一种新的思路和方法。为此，进一步对文献［3-4］中给出的n 重积分极限及其相关结论进行研究和推广，并采用蒙特卡罗法对其进行近似计算，同时利用局部加权回归拟合对其进行模拟。

3 一类推广的多重积分极限的概率方法求解与模拟计算

3.1 已有结论的修正与模拟计算

根据上述式(1)的n 重积分极限的概率求解过程，类似地可应用于对文献［3］给出的如式(9)所示的n 重积分极限的证明。

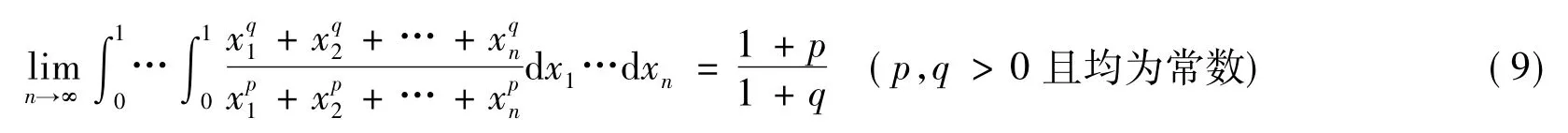
其中:文献［3］针对式(9)中参数p，q 的要求是q＞p 且q≠-1。显然，当(1+p)(1+q)＜0 时，式(9)中的结论不成立，所以结合文献［3-4］如定理1 所示的结论，参数p，q 的要求修正为p，q＞0 且均为常数。

定理1［3-4］设f(x)与g(x)都是［0，1］上的实值连续函数，若存在某个常数c＞0，有不等式0≤f(x)＜cg(x)成立，则有

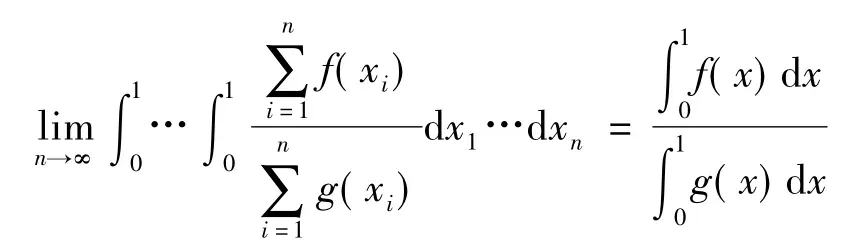
为了对式(9)的n 重积分极限过程进行模拟计算，类似式(7)、(8)的离散化过程，式(9)的n 重积分离散化为

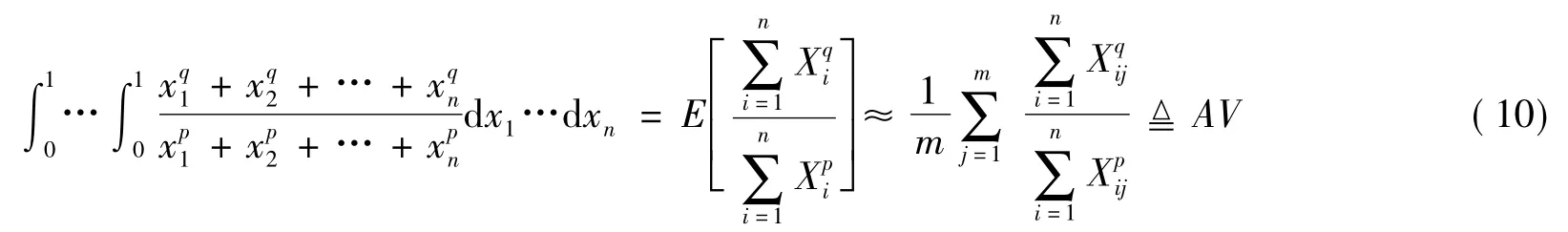
其中，连续性随机变量序列{Xi}(i=1，2，3，…，n)独立且同分布于［0，1］上的均匀分布。基于式(10)，得到如算法2 所示的蒙特卡罗模拟算法。

算法2:式(9)n 重积分近似求解的蒙特卡罗算法

利用算法2 和Lowess 拟合过程，对不同m 值(m=2 000，m=5 000)，当n 重积分的重数n 从100 以步长100 增加至10 000 时，式(9)的n 重积分的近似值AV、n→∞时极限值与Lowess 值LWRV的仿真散点图如图3 所示，这里p、q 分别取2 组不同值。通过图3 可以发现，随着重积分重数n 的不断增大，近似值AV 越来越接近n→∞时的极限值LV，并在极限值LV 附近随机波动，Lowess 拟合曲线也逐步逼近重积分的极限值LV，并且能看出参数p、q 修正为p，q＞0 是合理的。

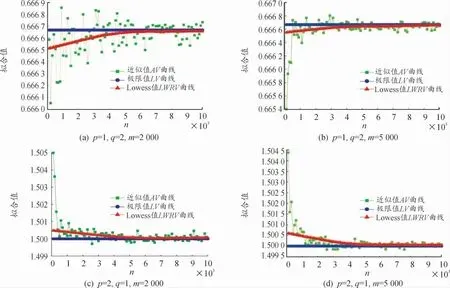
图3 不同m，p，q 值下(9)式n 重积分n 增加时AV、LV 与LWRV 的变化趋势

3.2 一类推广的多重积分的极限

定理1 是在［0，1］×［0，1］×…×［0，1］区域上n 重积的极限，该结论可进一步推广到区域［0，u］×［0，u］×…×［0，u］上，得到下列n 重积分的极限。

定理2设a(x)与b(x)为［0，u］上的实值连续函数，若存在某常数c＞0，使得0＜a(x)＜cb(x)成立，则有

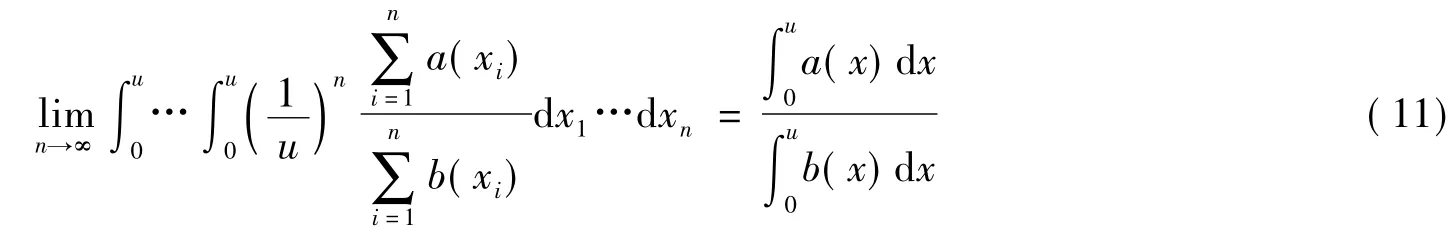
证明类似地，引入概率相关知识进行证明。假设连续性随机变量序列{Xi}(i=1，2，3，…，n)独立且同分布于［0，u］上的均匀分布，则随机变量序列{Xi}的联合密度函数为

记随机变量函数a(Xi)与b(Xi)的期望分别为

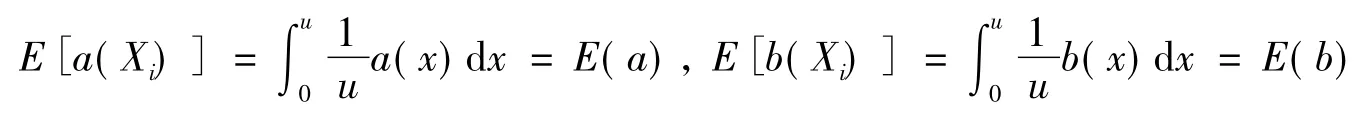
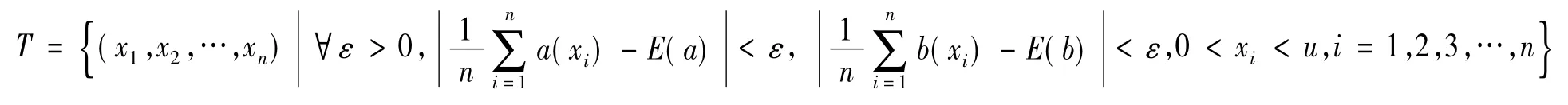
由于

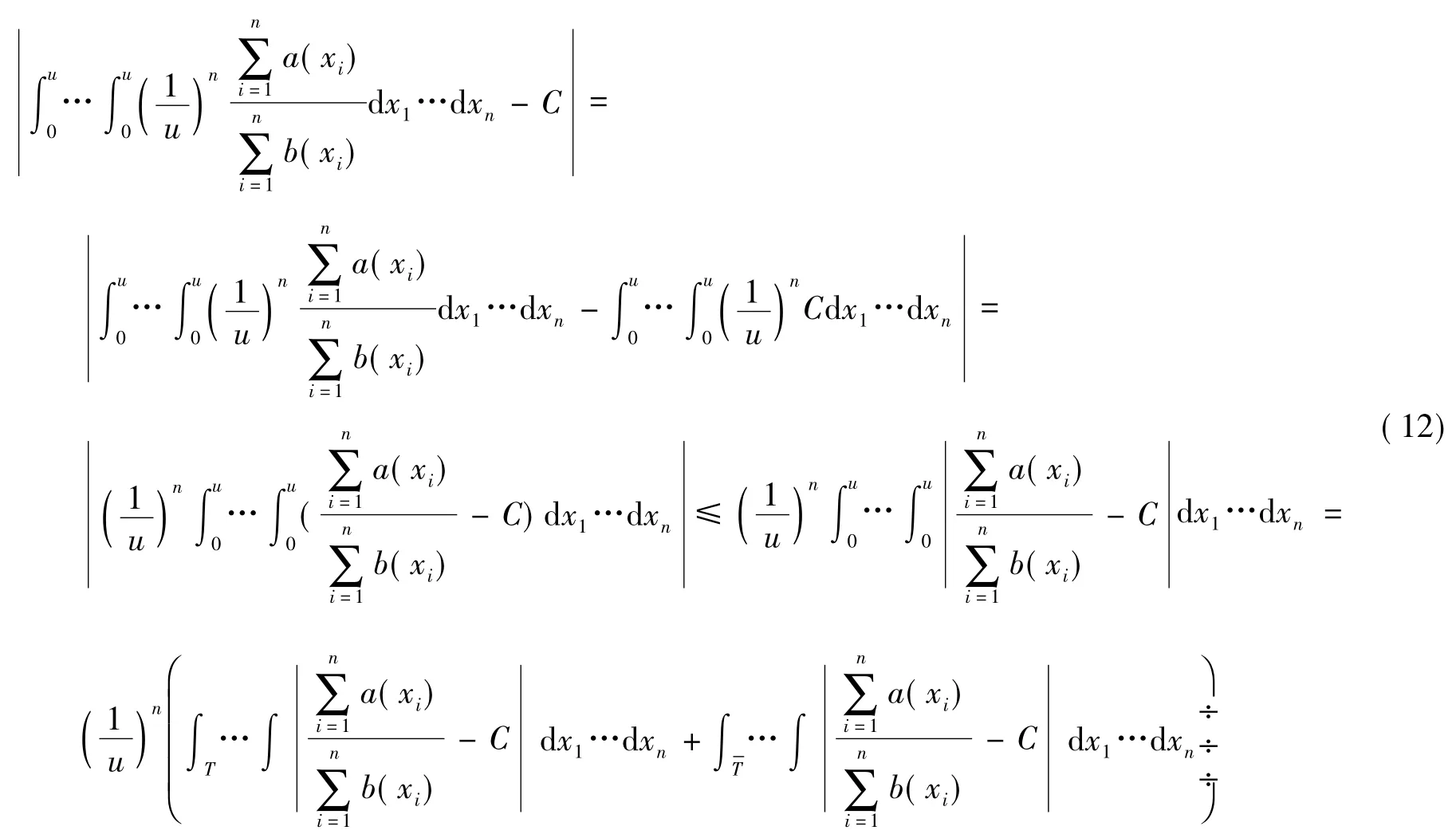
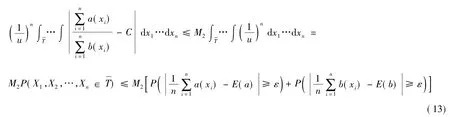
再考虑式(12)在积分区域T 上的情况。由于E(a)=CE(b)，所以

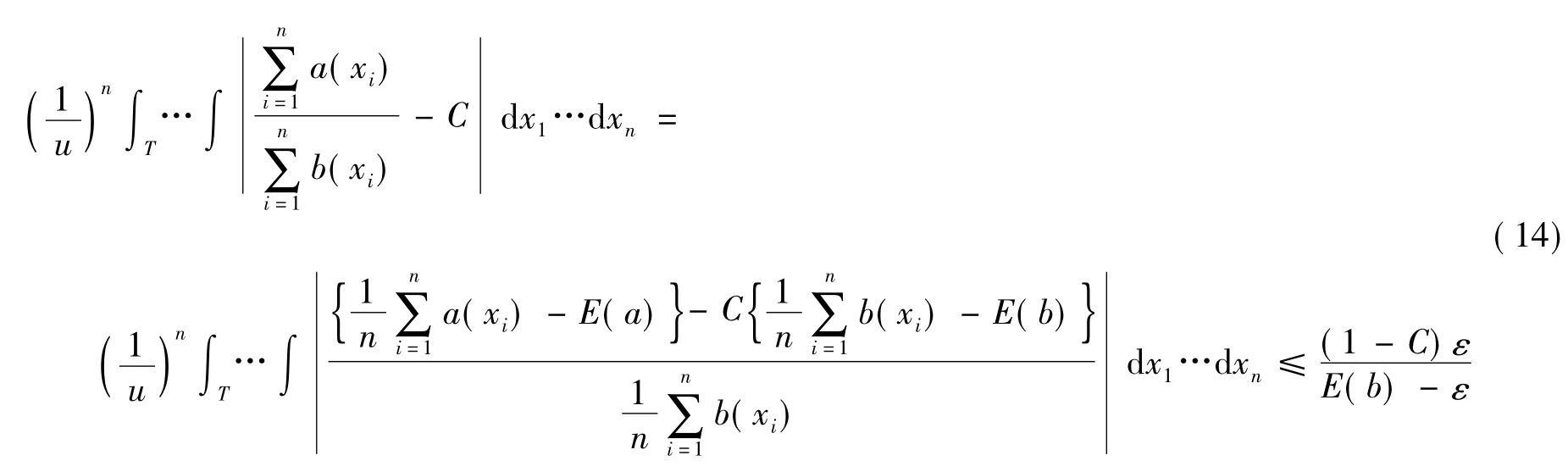
综合式(13)(14)，可得

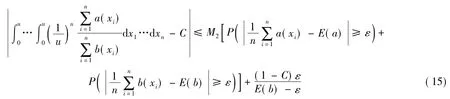
由辛钦大数定律以及依概率收敛可知［16］，对任意ε＞0 有

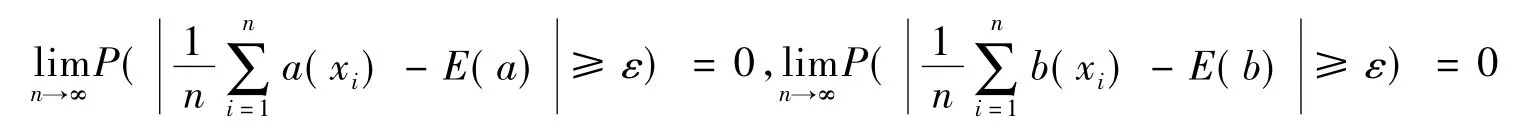
所以，对式(15)由极限的夹迫性定理［17］，可得

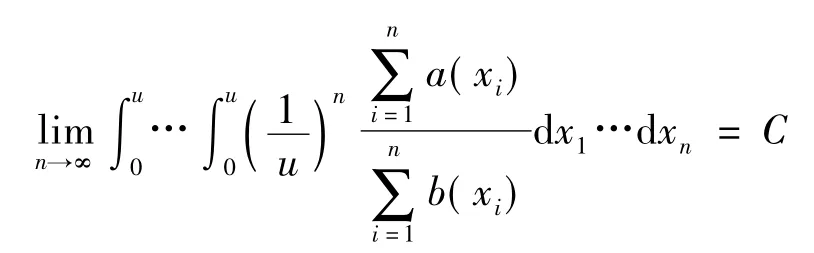
综上，式(11)得证。

3.3 推广的一类多重积分极限的模拟计算

根据定理2，结合式(9)的n 重积分极限，对式(16)的n 重积分及其极限利用蒙特卡罗法进行近似求解，并利用Lowess 曲线拟合进行模拟。

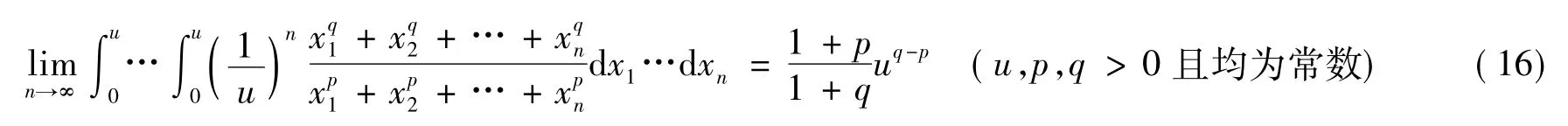
首先将(16)式n 重积分极限离散化为

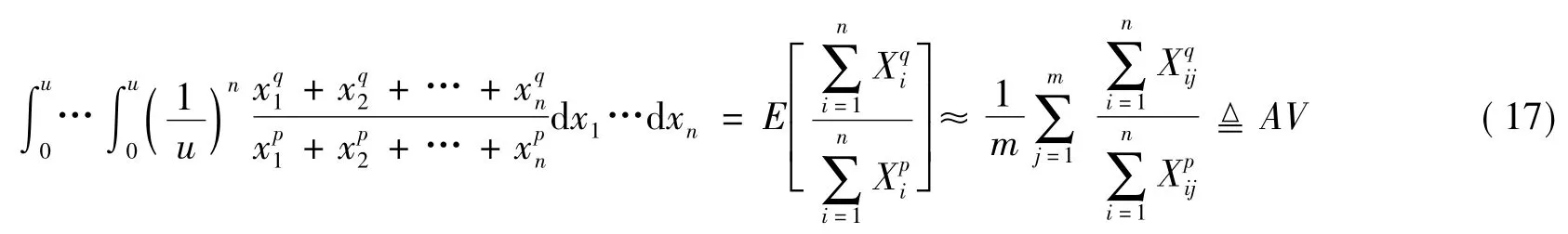
其中，连续性随机变量序列{Xi}(i=1，2，3，…，n)独立且同分布于［0，u］上的均匀分布。基于式(17)，得到如算法3 所示的蒙特卡罗模拟算法。

算法3:式(16)n 重积分近似求解的蒙特卡罗算法

为了对式(16)的n 重积分的极限过程利用算法3 和Lowess 拟合过程进行模拟计算，将积分区域中的参数u 按照0＜u＜1 和u＞1 两种情况取值，被积函数中的参数p，q 按照p＞q＞0 和0＜p＜q 两种情况取值，参数u，p，q 取值情况如表1 所示。当n 重积分的重数n 从100 以步长100 增加至10 000 时，式(16)n 重积分的近似值AV、n→∞时极限值与Lowess 值LWRV 的仿真散点图分别如图4、图5 所示。从图4 和图5 显示的结果中可以看出，当0＜u＜1 以及u＞1 时，在不同参数p，q 取值下，式(16)相应重积分的近似模拟值(AV 曲线)都能随着n 的增大逐渐逼近其极限值(LV 曲线)，数值计算结果表明，定理2 的结论是合理的。

表1 参数u，p，q 取值与n→∞时(16)式n 重积分的极限值

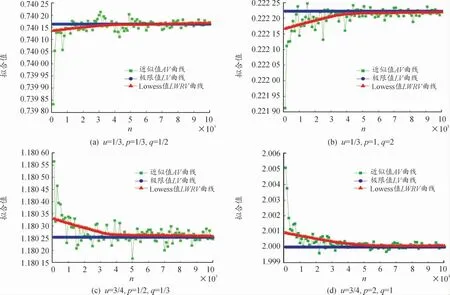
图4 当m=5 000，0＜u＜1，不同p，q 值式(16)n 重积分n 增加时AV、LV 与LWRV 的变化趋势

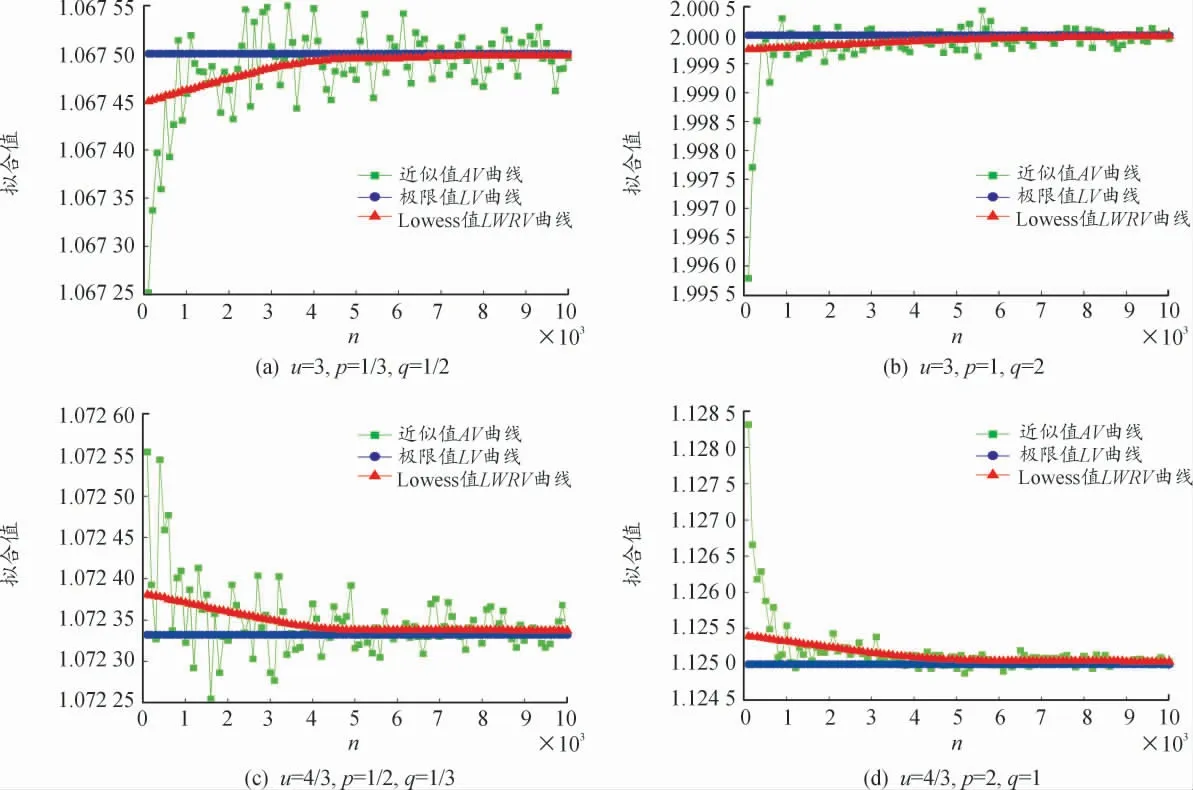
图5 当m=5 000，u＞1，不同p，q 值式(16)n 重积分n 增加时AV、LV 与LWRV 的变化趋势

4 结论

从概率论角度出发，通过构造适当概率论分布，在利用辛钦大数定律和依概率收敛定理等相关概率知识的基础上，对一类复杂n 重积分当n→∞时的极限问题进行了详细证明。基于多维连续性随机变量的数学期望与重积分之间的关系，对n 重积分进行离散化处理，并利用蒙特卡罗算法对离散化结果在n→∞时的极限过程进行近似计算和可视化。同时，利用一种非参数回归方法——Lowess 法对n→∞时的近似计算结果进行曲线拟合，发现Lowess 拟合曲线能较好地反映n 重积分收敛的可视化过程。