采用正交试验与RSM 的车辆冷却风扇降噪研究

朱茂桃，唐 杰，李 娜，田春虎

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

0 引言

轴流式冷却风扇是发动机冷却系统的关键部件，对保证发动机稳定运行意义重大。对于一款制造精准、装配合理的冷却风扇，噪声形式主要为气动噪声［1］。气动噪声一直是发动机冷却风扇设计时的制约因素，控制和降低风扇气动噪声对汽车降噪工程意义重大。

在国内外学者的风扇单体降噪研究中，张伟光等［2］运用三维升力面理论求解风扇噪声，详细研究了扇叶弯掠改型对风扇降噪的积极作用。李作伟［3］建立了多组吸风风扇对比模型，详细论证了通过优化动静叶片数量与安装角以改善噪声性能的可能性。李杨［4］通过CFD 仿真对风扇的周向倾角展开研究，并借助遗传算法实现了降噪设计。刘家成等［5］通过非光滑表面技术，发现叶片表面的凹坑结构对气动性能、绕流流场和噪声特性具有积极作用。叶紫阳［6］借助CFD 仿真，结合单一变量法对不同结构的非光滑叶片风扇进行计算对比，分析了不同结构参数对风扇的气动性能和气动噪声性能的作用。同航等［7］通过数值模拟发现波浪形前缘静子叶片能够使高速轴流风扇的离散噪声得到一定抑制。袁宏伟［8］发现拥有耦合仿生结构的叶片降噪效果明显，且能够保证风扇原有的气动性能。Park 等［9］通过研究叶片表面上的压力信息，分析了由模型和尾流相互作用引起的宽频噪声的来源。Biedermann 等［10］通过试验的方法发现风扇叶片引入前缘锯齿结构可以对2 000 Hz 以下的宽频噪声起到一定的抑制作用。王宽等［11］验证了考虑风扇风架的影响可提高气动噪声预测准确性。但这些研究仿真中较少考虑风架的气动作用，且缺少对平面叶型具体参数的优化研究。

为实现风扇平面叶型参数优化，达到降噪目的，充分考虑响应曲面法在风扇降噪问题中的适用性，针对冷却风扇平面叶型基本参数进行正交试验设计，得到噪声性能的敏感参数及最优参数水平潜在区间。在此基础上，经Box-Behnken 试验拟合出响应曲面代理模型并求解得到最优平面叶型参数组合。经CFD/CAA 耦合仿真验证了优化后风扇的声场与流场，为冷却风扇平面叶型参数优化设计建立了一套完整的分析流程。

1 涡声理论

涡声理论［12］认为，风扇在旋转过程中，叶片冲击气流使空气呈现涡状分布，而在气流发展过程中，涡流逐渐溃散消失造成能量变化，进而引发气动噪声。涡声理论改善了FW-H 方程和Lowson方程无法求解非周期性噪声的局限性，可有效提高风扇宽频涡声的计算精度。涡声方程为:

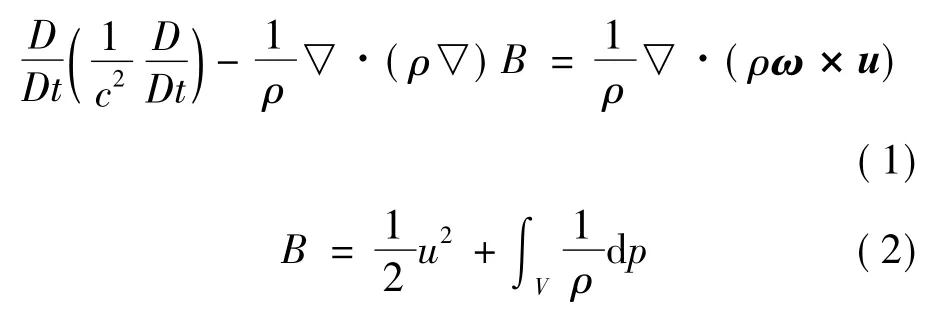
式中:B 为空气流总焓，c 为声速，D 为湍动能，ω 为涡矢量，u 为速度矢量，ρ 为空气密度。为去除对计算精度影响较小的冗杂因素，将空气视为不可压缩的恒温流体［13］。则式(2)可简化为:

等式(3)左侧项描述声场传播过程，右侧项为气流涡声源。不难发现，若涡量为0，则噪声值也为0，可直观表明噪声与空气涡量的紧密联系。

2 CFD/CAA 联合仿真

2.1 流场计算

研究对象为某款8 叶片轴流吸风式风扇，其风扇外径为390 mm，轮毂直径为158 mm，轮毂比为0.4，导风罩内径为400 mm，宽为95 mm。以满足计算精度要求为前提，建立仅保留电机主体结构、风架以及风扇的简化模型。模拟真实试验状态，建立直径为396 mm 的圆柱形包络体包裹环形叶片模型以模拟扇叶近壁面处的气流状态。建立横截面与试验风门截面一致(1 000 mm ×1 000 mm)、长度为4 000 mm 的长方体，并进行布尔求差，即得风洞模拟模型，如图1 所示。该模型可有效避免仿真计算时回流现象的产生。

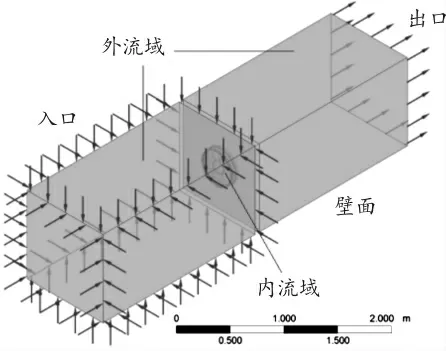
图1 风扇流场计算模型示意图

为在保证计算精度的同时控制计算量，经网格无关性验证，对风扇流场计算模型的内流域与外流域分别定义不同的网格密度及合适的相关度，均选用自适应强的四面体网格单元，对扇叶附近网格进行加密处理［14］。最终，将内、外流域的网格尺寸分别设置成2 mm 与20 mm，网格总数约260 万。

进行冷却风扇稳态流场计算，各项设置如下:空气入口设为相对静压为0 Pa 的速度入口，出口设为与试验静压一致的压力出口，除了入口处的5个面、出口处的1 个面以及内外流域的交界面，其余壁面为无滑移绝热壁面(如图1 所示);湍流模型选用标准k-ε 模型，方程离散格式为二阶迎风差分格式。在求解稳态流场结束之后，将求解的结果作为初场再进行瞬态计算，从而求解出叶片表面的压力脉动值。借助LES 大涡模拟，在内外流域交界面选用瞬态转子定子插值方法，采样频率与时间步长遵循保证计算准确性且节约计算资源的原则，根据下式确定［15］:

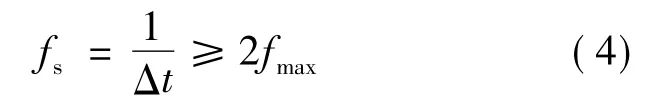
式中:fs为采样频率;Δt 为时间步长;fmax为采样信号截止频率，据试验可知噪声分析的fmax值为2 500 Hz。

2.2 声场计算

待冷却风扇的气动性能分析结束后，依据式(1)计算出涡声源分布，利用涡声理论定性分析涡量与噪声的关联。将风扇视为紧致声源，截取残差曲线中稳定转动5r 区间内脉动平稳的流场数据并导入LMS Virtual.lab 软件，经积分变换得到各坐标轴方向的等效旋转偶极子声源。导入风架孔网格作为风扇噪声边界以模拟风架孔对风扇声场的作用。采用间接边界元法建立半径为1 m、球心为风扇中心点的球形场点网格，并将风扇轴线与球面交汇点作为声压级监测点，最终建立的声场计算模型如图2 所示。按照试验工况(实测转速2 471 r/min，出口静压0.8 Pa)，依据涡声理论及Lowson 方程，同时求解时域条件下的宽频噪声及离散噪声，并记录两监测点处的声压级。

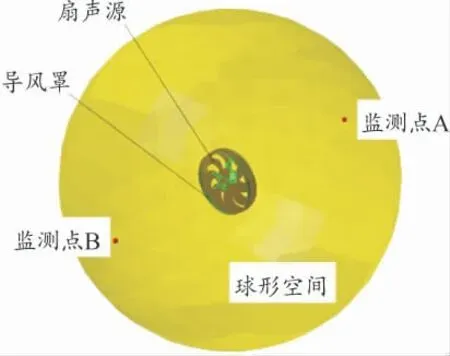
图2 声场计算模型示意图

2.3 噪声试验验证

为验证气动声学的仿真结果，在半消音室环境中完成风扇噪声性能试验，进出口噪声监测点布置位置与声学仿真模型相同，采用B＆K PULSE 3 560 B 多分析仪采集风扇噪声数值，具体噪声性能试验布置及试验场景如图3 所示。

图3 冷却风扇噪声性能试验布置及试验环境

图4 为风扇进气侧A 点处的声压级频谱试验值与仿真值。可以发现:监测点A 处的数值计算结果与试验结果具有一致的波动趋势，风扇噪声以低频离散噪声为主导，且均在二阶谐频处达到最大峰值;A 点处的声压级仿真结果较试验值略低，且宽频噪声仿真误差大于离散噪声仿真误差，误差原因总结如下:①数值仿真结果存在偏差，如未精确模拟风架附近因空气涡流引起的噪声;②因风扇噪声试验环境为半消音室环境，该环境下会出现声波反射及折射现象，造成试验误差;③风扇实际工作时产生的扇叶振动噪声及电机电磁噪声会增大噪声试验监测值。声压级离散趋势与数值均符合试验结果，可凭此CFD/CAA 耦合仿真方法对风扇噪声做进一步研究。

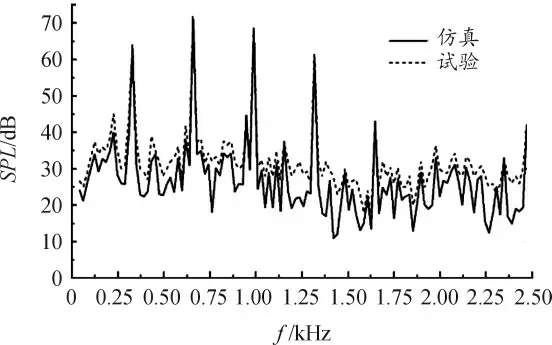
图4 A 点处声压级频谱

3 正交试验设计

3.1 试验目的

为明确风扇噪声的敏感平面叶型参数，以实测转速2 471 r/min、出口静压0.8 Pa 工况为例对风扇平面叶型参数进行正交试验设计，并借助试验结果分析各变量对风扇气动噪声性能与气动性能的作用趋势。

3.2 方案确定

图5 为轴流冷却风扇叶片平面叶型示意图。其中，叶背、前缘、叶盆和后缘共4 条曲线封闭构成平面叶型，参数对冷却风扇整体造型及气动噪声性能作用明显。以原型冷却风扇模型为优化对象，选用双多项式模型［16］拟合中弧线和厚度曲线，对叶片参数进行参数化表达。

图5 平面叶型示意图

对冷却风扇进行参数化建模时，确定对平面叶型作用较强的7 个独立参数，即中弧线上的内弦长(B0)、最大相对挠度(Fmax)、最大挠度相对位置(Pmax)、厚度曲线上的最大相对半径(Rmax)、最大半径相对位置(Tmax)、相对前缘半径(R1)和相对后缘半径(R2)。利用正交试验研究平面叶型参数对风扇结构及性能的影响，为尽量避免其他因素对分析优化结果产生影响，依然将原型风扇的风架模型装配到参数化模型中。综合考虑各参数的相关性及风扇内流场分布特点，最终确定的试验因素与试验水平数据如表1 表示。

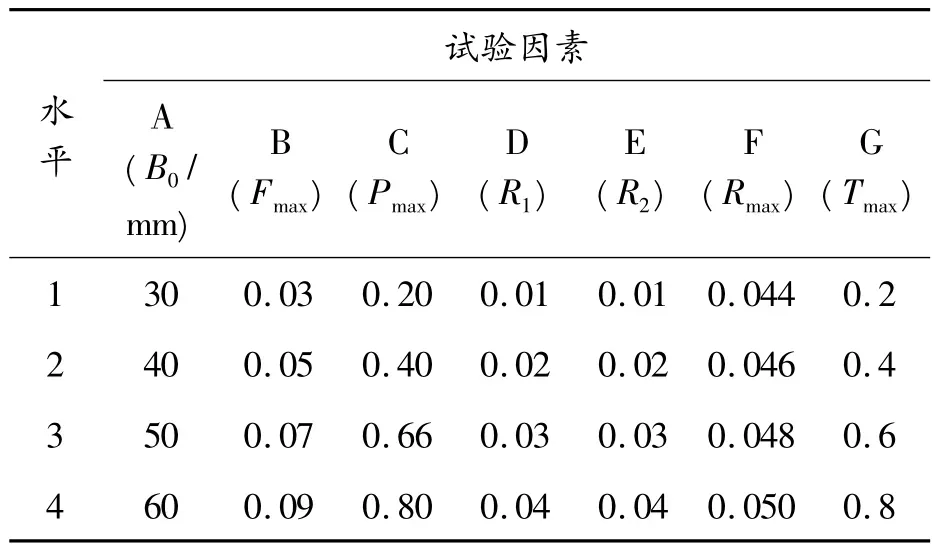
表1 试验因素及水平数据

为探究各试验因素对冷却风扇的标准风量及进风口噪声总声压级的作用效果，在不降低风扇气动性能的前提下改善其噪声性能，参照L32(49)标准正交试验表可得32 种平面叶型设计方案，如表2 所示，其中:A～G 为各试验因素代号，H、I 为空列。

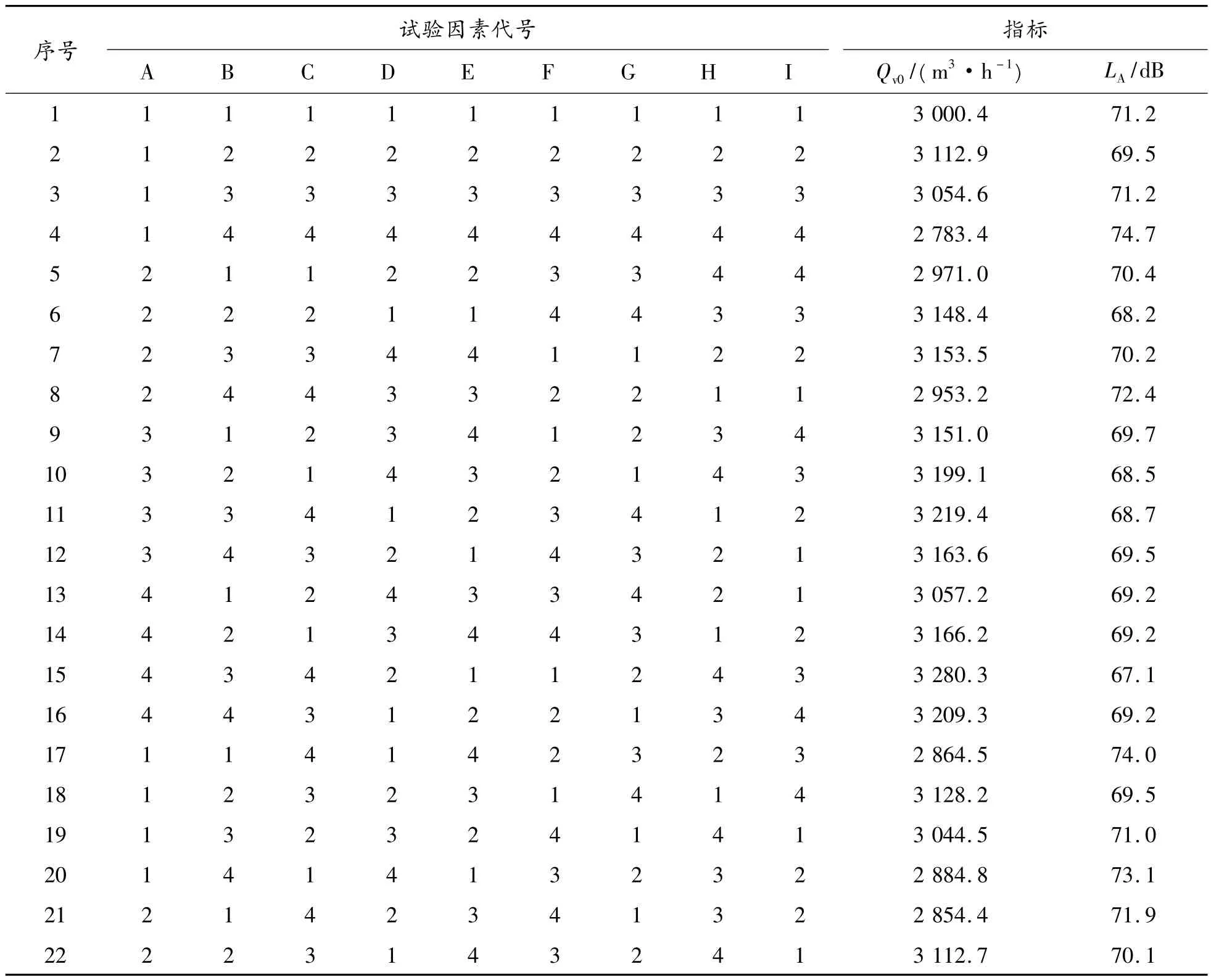
表2 正交试验方案和结果

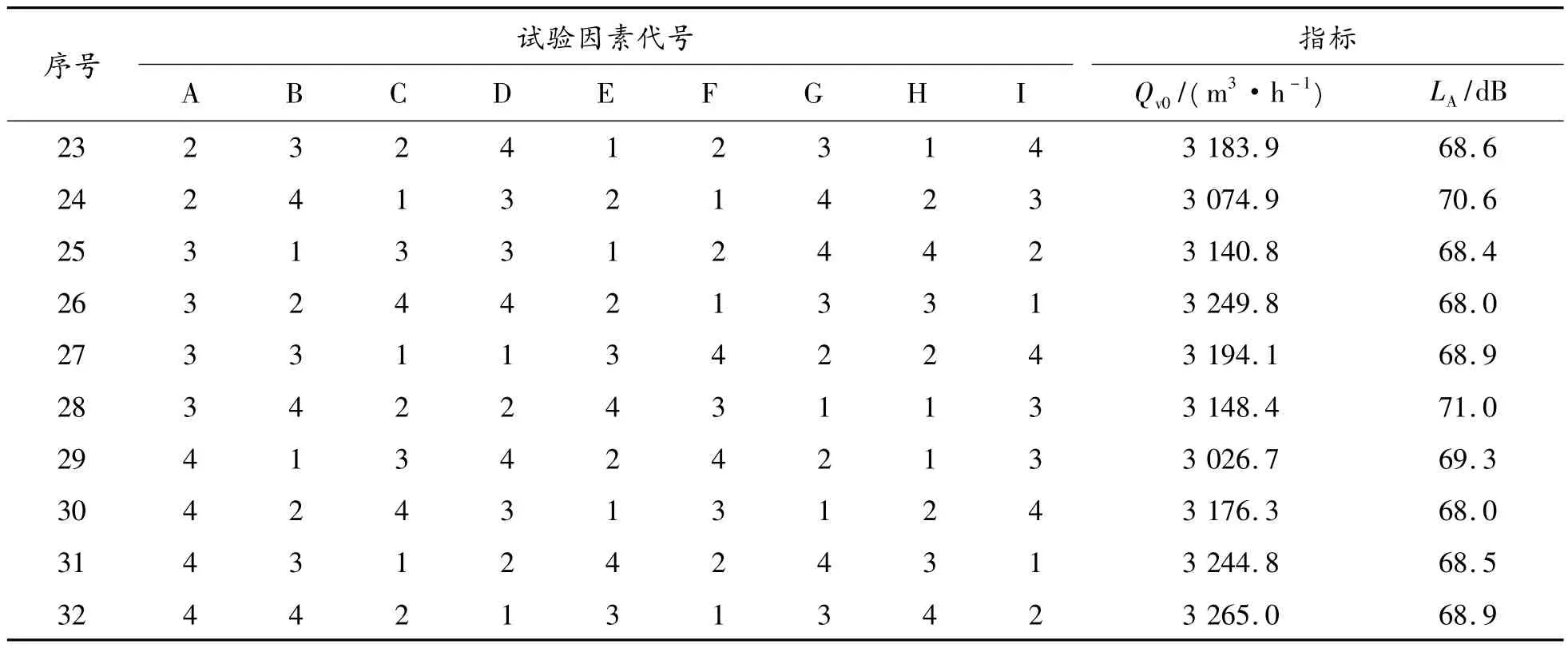
续表(表2)

3.3 极差分析

将表2 中各平面叶型参数组合导入三维风扇参数化模型，并应用前述的CFD/CAA 联合仿真方法对32 款风扇模型进行求解，标准风量Qv0、进风口噪声总声压级LA的数值仿真结果如表2 所示。为进一步明确各因素水平的作用效果，通过极差分析法对平面叶型正交试验结果进行更为直观的表达，分析结果见表3。其中，H 列与I 列2 个空列对标准风量的极差值仅为3.70 与3.67，对进风口噪声的极差值仅为0.10 与0.11，相较于其他参数所对应的极差值显得很小，由此表明试验中偶然误差较小。

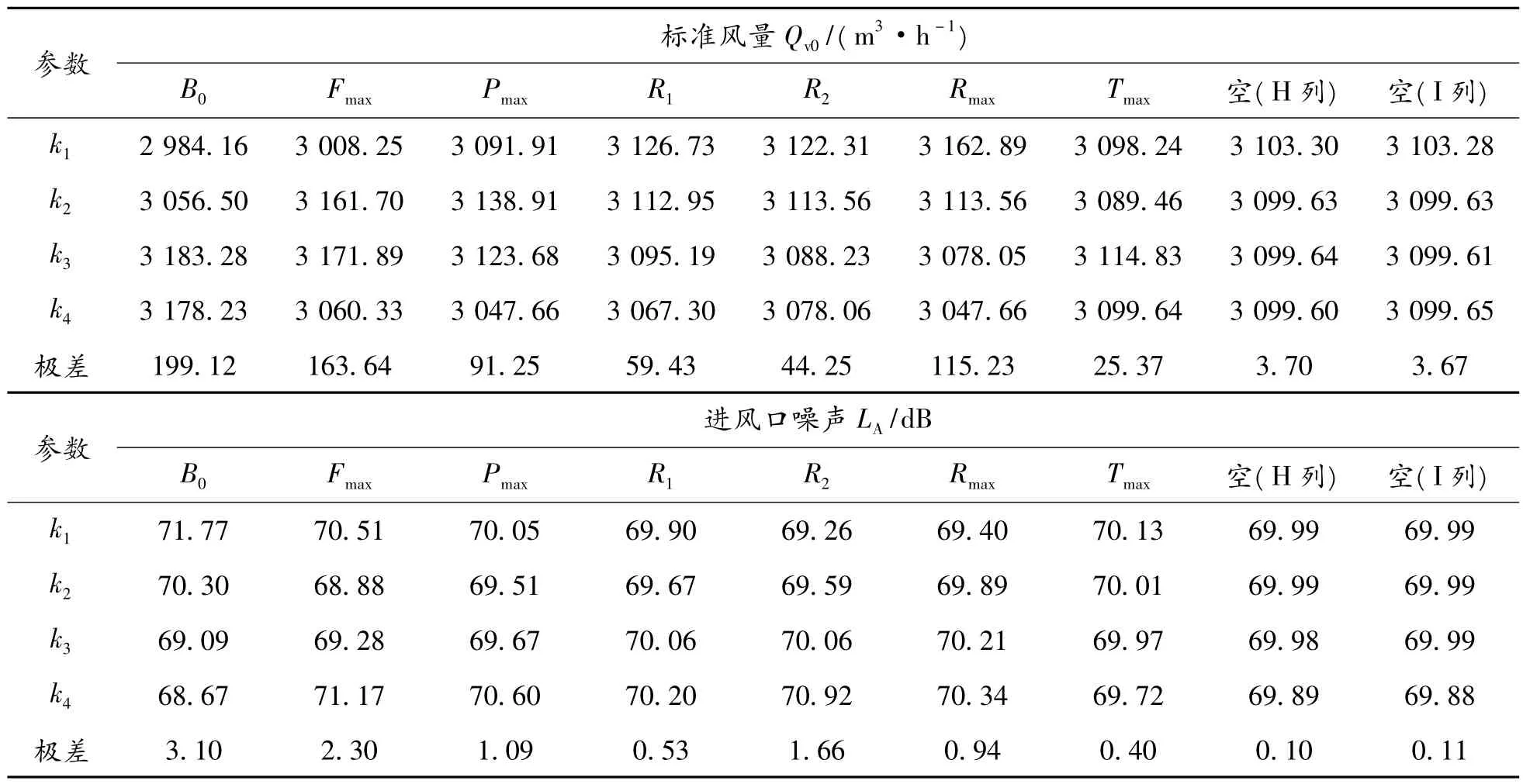
表3 极差分析结果

在极差分析法中，极差R 值越大，则该因素对评价指标的敏感性越大［17］。因此，对比表3 中的R 值可得:内弦长B0与最大相对挠度Fmax对冷却风扇标准风量及进风口噪声声压级的影响颇为显著，厚度曲线上的最大相对半径Rmax对风扇的标准风量的影响比较显著，后缘半径R2对风扇进风口噪声声压级影响比较显著。其中，各因素对冷却风扇标准风量的影响显著程度由大到小依次为A、B、F、C、D、E、G，对于风扇进风口气动噪声值，各因素的影响显著程度由大到小为A、B、E、C、F、D、G。通过比较表3 中各个因素不同水平对于进风口噪声的平均效果值，可以确定降噪效果最优的水平组合为A4、B2、C2、D2、E1、F1、G4，即B0=60 mm、Fmax=0.05、Pmax=0.4、R1=0.02、R2=0.01、Rmax=0.044、Tmax=0.8。

基于以上分析，为进一步明确各平面叶型参数对冷却风扇性能的作用效果，结合表1 和表2的正交试验结果，把各平面叶型参数的4 个水平值作为横坐标，把风量和噪声的试验值作为纵坐标，分别绘制折线图以更加清晰地反映趋势走向，如图6 所示。

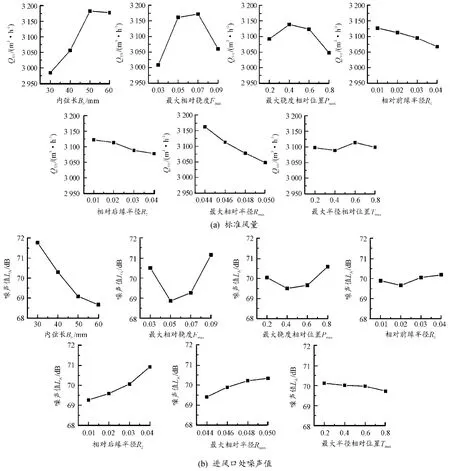
图6 各参数对风扇性能影响趋势曲线

对比图6(a)(b)中各因素的影响趋势走向不难得出:适当增大中弧线的内弦长度、减小厚度曲线的后缘半径值以及最大相对半径、选择合适的最大相对挠度范围，可有效降低冷却风扇噪声值。与此同时，风扇的进口风量也会随之增大。分析原因如下:增大平面叶型的中弧线内弦长，可增大扇叶与空气的接触面积，为受到叶片作用力的空气提供更加充足的流动、转向空间，从而减缓气流对叶片的冲击，风扇噪声性能与气动性能随之改善;叶片工作面与非工作面两侧的高速气流于叶片后缘处交汇，减小后缘半径可缩减叶片后缘处因气流交汇形成的真空地带，可有效避免涡流现象的产生，进而降低噪声;同样，减小最大相对半径，可以减小叶片吸力面的弯曲程度，避免吸力面表面凸起现象的发生，使气流可以处于更广的顺压梯度区，从而有效推迟边界层由层流向湍流的转捩，减小尾涡强度，提高风扇的气动性能和噪声性能;选择合适的最大相对挠度可减轻叶片压力面对气流的阻碍作用，也可减小涡流区域面积，改善风扇的噪声性能与气动性能。

综合以上分析，可发现平面叶型参数对风扇风量与噪声具有相似的作用趋势，即改变平面叶型参数优化风扇噪声性能的同时，气动性能也会随之优化，因此在对风扇进行响应曲面法优化时，只采用噪声值的单一评价指标即可。

4 基于RSM 的平面叶型参数优化

4.1 Box-Behnken 试验

Box-Behnken 试验是目前构造响应面的常用方法［18-19］。经正交试验分析，可得出对冷却风扇空气入口处噪声值影响较大的因素为B0、Fmax、Rmax及R2，以此作为Box-Behnken 试验的试验因素。依据极差分析结果及图6 中的折线趋势，估算出利于改善噪声评价指标的最佳参数范围作为Box-Behnken 试验的水平值。具体方案设计及噪声值仿真结果如表4 所示。

表4 Box-Behnken 试验方案和结果

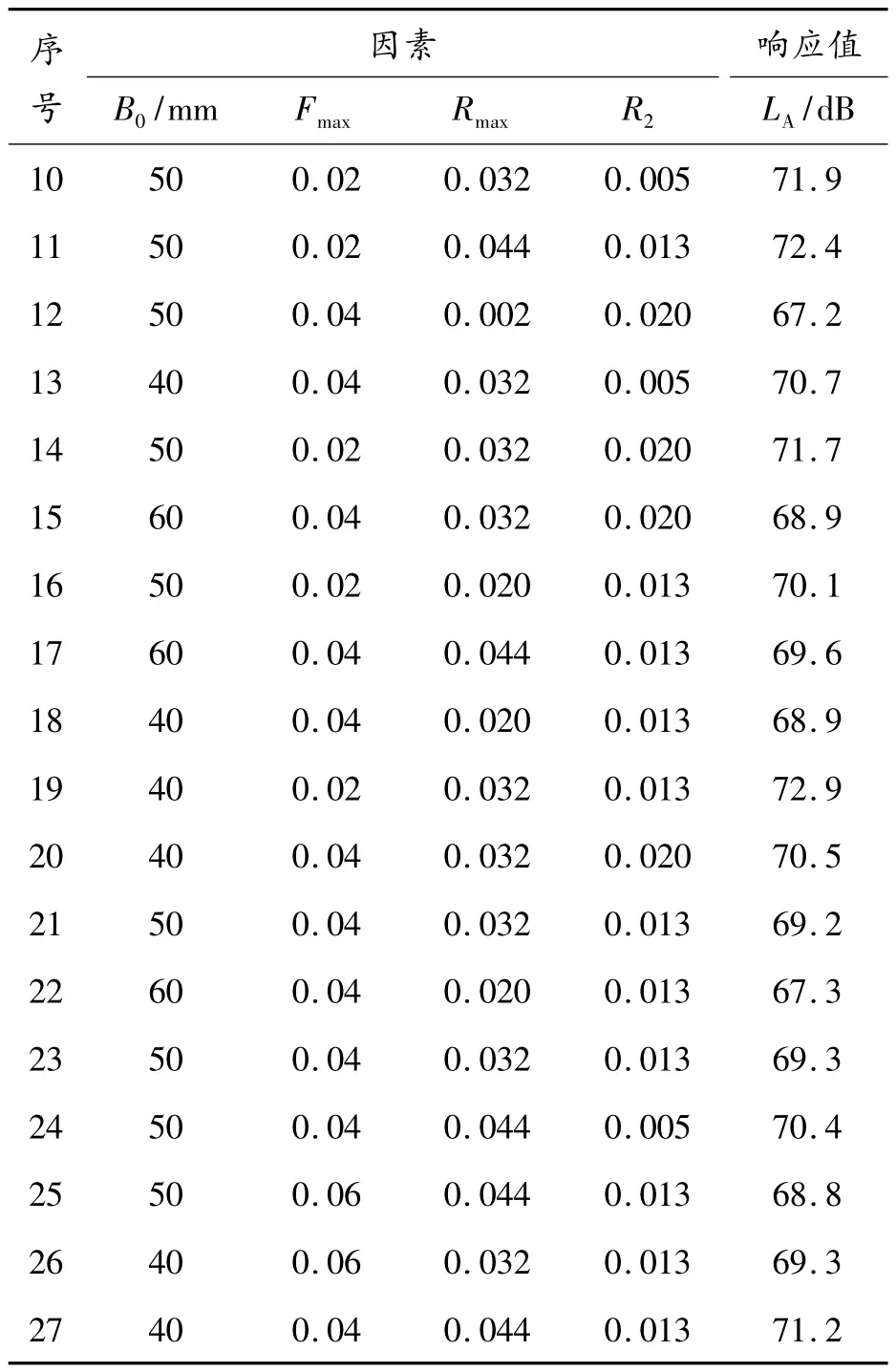
续表(表4)

4.2 回归模型构建

参照RSM 模型的二次多项式表达方法［20］，拟合噪声响应值的试验结果，得到噪声声压级的回归方程:

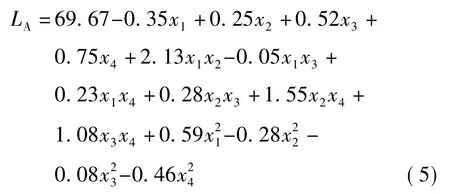
为验证式(5)在风扇降噪优化问题中的合理性，应用SAS 软件对模型进行方差分析，结果如表5 所示。其中，计算该回归方程的校正决定系数=0.913 3，表明回归模型中的变量可涵盖91.33%的噪声值范围，代理模型拟合作用显著。x2、x1x2的P 值均低于0.01，x2x4的P 值低于0.05，表明该响应面回归模型满足模拟真实试验点的显著性要求。

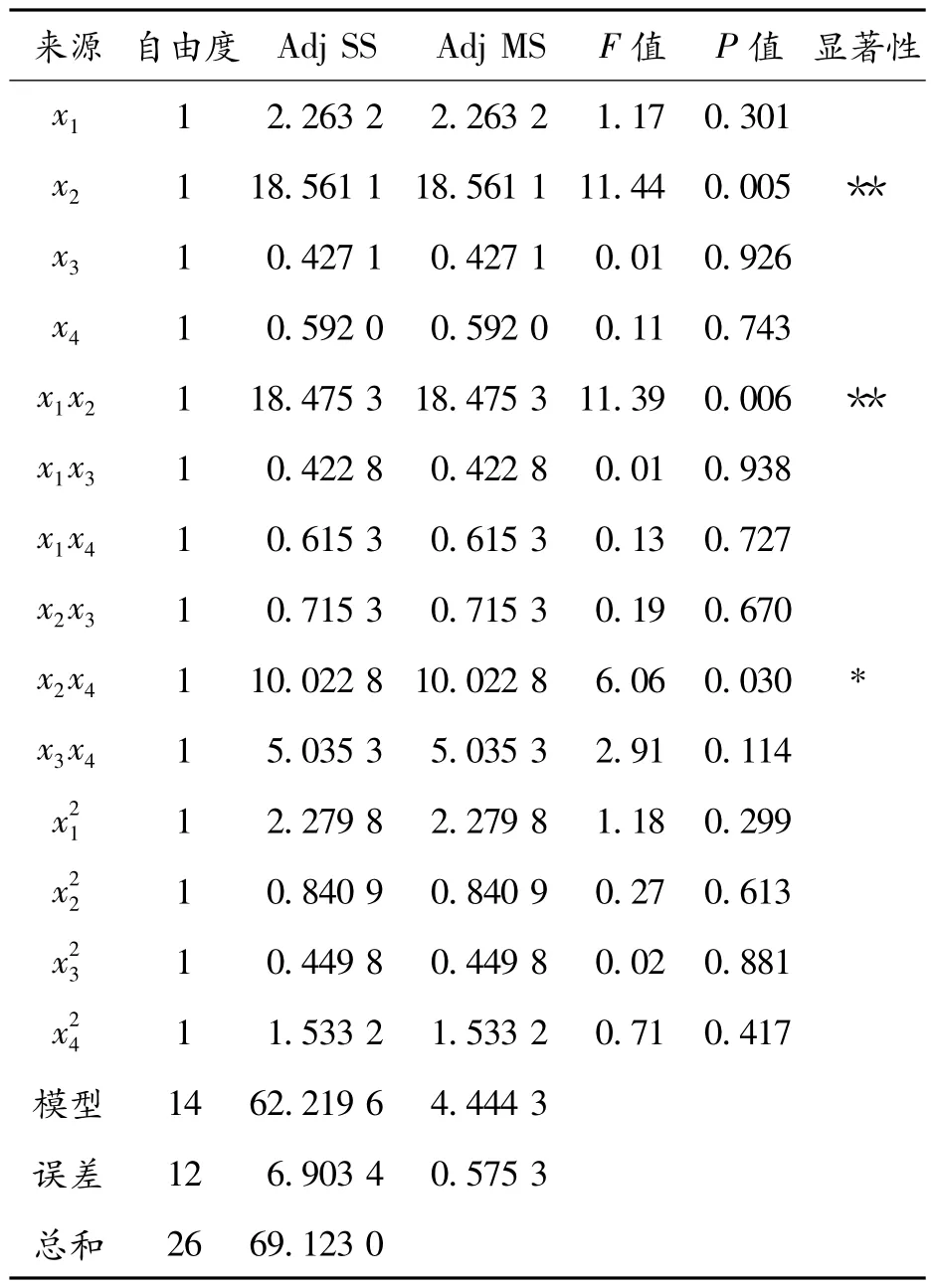
表5 噪声值LA 的回归方程方差分析

为明确后缘半径R2、内弦长B0、最大相对挠度Fmax及最大相对半径Rmax之间的交互作用对噪声响应面波动的影响情况，绘制如图7 所示的响应面。

图7 各试验因素对噪声值LA 的响应面示意图

4.3 优化方案及数值验证

以寻求最小噪声值为最终优化任务，求解响应面回归模型的最优值，经正交试验结果填充，最终确定的最优参数组合为:B0=57.53 mm、Fmax=0.066、Pmax=0.4、R1=0.02、R2=0.02、Rmax=0.026、Tmax=0.8，RSM 代理模型预测优化后的风扇总声压级为66.28 dB。而优化前总声压级为70.80 dB。

对平面叶型参数优化后的风扇参数化模型通过CFD/CAA 进行仿真验证，如图8 所示为优化前后A 点(进风口)处噪声声压级频谱。由图8 可见:优化后的冷却风扇声压级分布变化较为显著，进风口A 点处的高频涡流噪声值虽有增加，但低频离散噪声的离散程度及声压级峰值均有明显降低，且A 点处噪声总声压级为66.83 dB，较优化前下降5.6%，离散噪声峰值下降19 dB。经CFD 稳态流场计算，其进口风量较初始模型增加3.4%。由此说明，该RSM 优化方案在不减弱冷却风扇风量的前提下，实现了对风扇噪声性能的大幅优化，达到了优化设计目标。

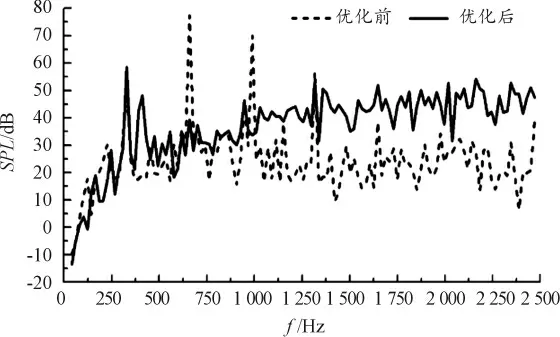
图8 优化前后监测点A 处声压级频谱

5 结论

1)应用CFD/CAA 联合仿真方法，在冷却风扇流场分析基础上完成噪声性能计算，通过半消音室环境下的噪声性能试验验证了CFD/CAA 联合仿真方法在风扇气动声学计算中的关键作用。

2)通过正交试验及极差分析，确定对气动噪声性能和气动噪声性能影响较大的平面叶型参数为B0、Fmax、Rmax及R2，且各参数对气动性能与噪声性能的影响趋势相似。

3)在正交试验基础上，依托RSM 拟合出预测冷却风扇噪声的代理模型，模型的校正决定系数=0.913 3，拟合良好，可准确反映风扇噪声声压级对各平面叶型参数的响应结果。

4)经响应面分析最终确定以噪声优化为目标的平面叶型参数优化方案，经验证，优化后的冷却风扇模型噪声总声压级为66.83 dB，下降幅度达5.6%，气动性能也有小幅改善，说明响应曲面法适用于冷却风扇的降噪优化设计。