针对汽车最速操纵稳定性的轮胎参数优化

张丽霞，王亚平，潘福全，刘家琪

(青岛理工大学 机械与汽车工程学院，山东 青岛 266520)

0 引言

汽车最速操纵稳定性即研究汽车在不超出给定路径边界的情况下，能够按照驾驶员的意愿以最快的速度通过路径的能力。轮胎与地面直接接触，对汽车的最速操纵稳定性有重要影响。通过优化轮胎设计参数，能够有效改善汽车最速操纵稳定性［1］。

Bagheri 等［2］利用多目标遗传算法优化了悬架的3 个重要参数，提高了操纵稳定性。Zhang等［3］以双横臂前悬架和多连杆后悬架车辆为例，基于双变道模拟试验，以最速操纵稳定性为评价指标优化了悬架的3 个参数。王国林等［4］利用Simulink 建立整车模型，并选用Gim 非线性轮胎理论模型，利用神经网络构建了前后轮侧偏刚度与操纵稳定性之间的映射关系。景立新等［5］进行轮胎的纯侧偏试验、复合工况试验等，结合ADAMS/CAR 软件建立轮胎及整车模型，研究不同侧偏刚度对整车操纵稳定性的影响。韦勇等［6］通过Matlab 将PAC 轮胎模型接入到CarSim 建立的整车模型，分析了轮胎力学特性因子对整车操纵稳定的评分影响，结果表明，轮胎侧偏刚度及附着系数的比例因子适当增大，对整车操纵稳定性有一定的改善。Ali 等［7］建立重型客车轮胎的有限元模型，研究了路面条件、充气压力、车速等对滚动阻力和侧偏特性的影响。El-sayegh 等［8］建立宽底卡车轮胎在湿滑路面上的有限元模型，分析了充气压力、水深、转角等对轮胎滚动阻力和侧偏特性的影响。Hassan 等［9］通过魔术公式轮胎模型研究了不同的轮胎附着系数对车辆侧翻和横向稳定性的影响，结果表明，轮胎的附着能力对车辆横向稳定性和侧翻倾向的影响是相反的。卢荡等［10］在2020 年通过实验得出的六分力数据推导了轮胎磨损情况对侧偏特性的影响。孙晓峰等［11］采用正交试验设计与单变量分析相结合的方法，研究带束层角度、带束层宽度、三角胶高度等轮胎结构参数对六分力中侧偏刚度和回正刚度的影响。

尽管国内外研究人员在针对操纵稳定性的优化方面做了大量研究，但优化参数通常为悬架、车身等刚体部件的质量、位置等设计参数，部分文献也研究了轮胎对操纵稳定性的影响，但多为利用轮胎经验模型、理论模型等研究轮胎侧偏刚度等轮胎特性对操纵稳定性的影响［12］。对轮胎的优化研究也仅从轮胎所表达的侧偏和纵滑等力学特性入手，寻找轮胎设计参数对侧偏等轮胎特性的影响。也就是说，现阶段我国轮胎厂商往往通过精细的有限元模型对单个轮胎进行仿真分析及优化设计，通过纵滑和侧偏等特性，间接评价该轮胎用于整车时的操纵稳定性。另外，对最速操纵稳定性的优化研究也较少。

针对目前操纵稳定性领域对轮胎设计参数的优化研究往往停留于纵滑、侧偏特性的现象，将轮胎与目前研究较少的汽车最速操纵稳定性结合，实现轮胎设计参数优化。以三菱蓝瑟汽车为例，在通过参数辨识将轮胎有限元模型与整车多体动力学模型结合的基础上，以轮胎的带束层帘线角度、带束层帘线宽度、充气压力、胎面橡胶弹性为优化变量，以最速操纵稳定性综合评价指标为优化目标，实现从整车最速操纵稳定性的角度针对轮胎设计参数进行优化。

1 轮胎和整车模型建立

首先在ABAQUS 中建立拥有复杂花纹的205/55R16 半钢子午线轮胎有限元模型，并对轮胎进行有限元分析。然后在基本粒子群算法上加入自适应权重和自然选择性，在Matlab 中利用改进后的粒子群算法，根据有限元试验数据对PAC89 轮胎模型的参数进行两级辨识。通过参数辨识，将轮胎有限元模型转换为稳态工况下用于操纵稳定性虚拟仿真的PAC89 轮胎模型。最后在ADAMS 中建立三菱蓝瑟的整车模型，并在整车模型上应用辨识得到的PAC89 轮胎模型。其中轮胎有限元模型如图1 所示。

图1 轮胎有限元模型示意图

轮胎模型部分参数如下:扁平率为55%，充气压力为0.24 MPa，部分橡胶材料参数如表1 所示，部分帘线材料参数如表2 所示。

表1 橡胶材料参数

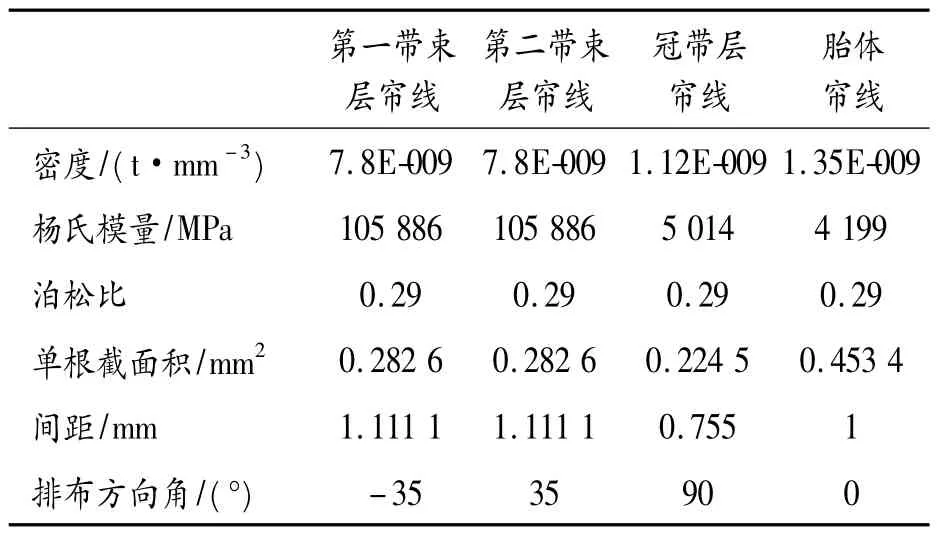
表2 帘线材料参数

2 优化变量与优化目标的确定

2.1 优化变量

轮胎的纵向力、侧偏力和回正力矩特性均会影响整车的操纵稳定性，因此，影响这三方面的轮胎参数均会对整车操纵稳定性造成影响［13］。

综合文献［14-18］中轮胎各参数对轮胎侧偏等特性的影响分析和有限分析结构，并考虑对轮胎振动、耐磨等其他因素影响，选择带束层帘线角度x1、充气压力x2、胎面胶弹性倍数x3和带束层宽度x4为优化变量。优化变量在试验设计中的水平如表3 所示。

表3 轮胎试验设计参数范围及其在试验中的水平

以轮胎周向为0°基准方向。表3 中，带束层帘线角度为单层角度，因2 层带束层帘线角度对称，表明一层角度为45°，则另一层角度为-45°;胎面胶弹性倍数指yeoh 模型系数的倍数;带束层宽度为上下2 层带束层宽度的平均值。

2.2 优化目标

采用文献［19］所提出的最速操纵稳定性综合评价指标，该指标综合考虑了操纵动力学和操纵逆动力学。

优化目标为由驾驶员负担评价指标JB、轮胎抓地能力评价指标JG、侧翻危险评价指标JR、侧滑危险评价指标JS、响应性评价指标JRP和动力性评价指标JP组成的最速操纵稳定性综合评价指标JT。

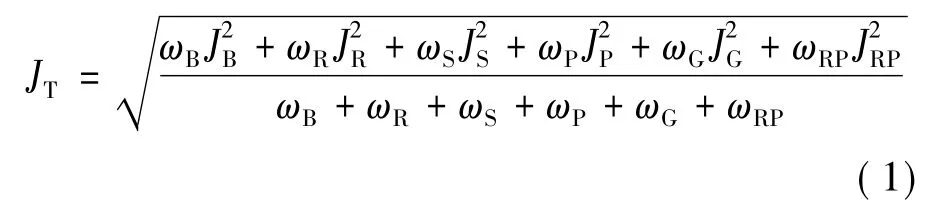
式中:ωB、ωR、ωS、ωP、ωG、ωRP为相对应评价指标的加权值。各评价指标的计算公式及本文采用的各门槛值和加权值可由文献［20］得到。

3 响应面优化设计

响应面优化设计具有计算速度快、稳定性高和寻优能力强的特点，因此，选用响应面二次多项式模型，其模型多项式如下:

式中:JT为优化目标;xi为设计变量;ki为一次项的待定系数，kii和kij为二次项的待定系数。

3.1 试验设计方法

采用4 因素3 水平的优化研究方法，选用中心复合表面设计(central composite-face-centered design，CCF)，将4 个优化变量作为设计变量，根据CCF 规则制作试验设计(design of experiment，DOE)表，共设计28 次试验，如表4 所示。

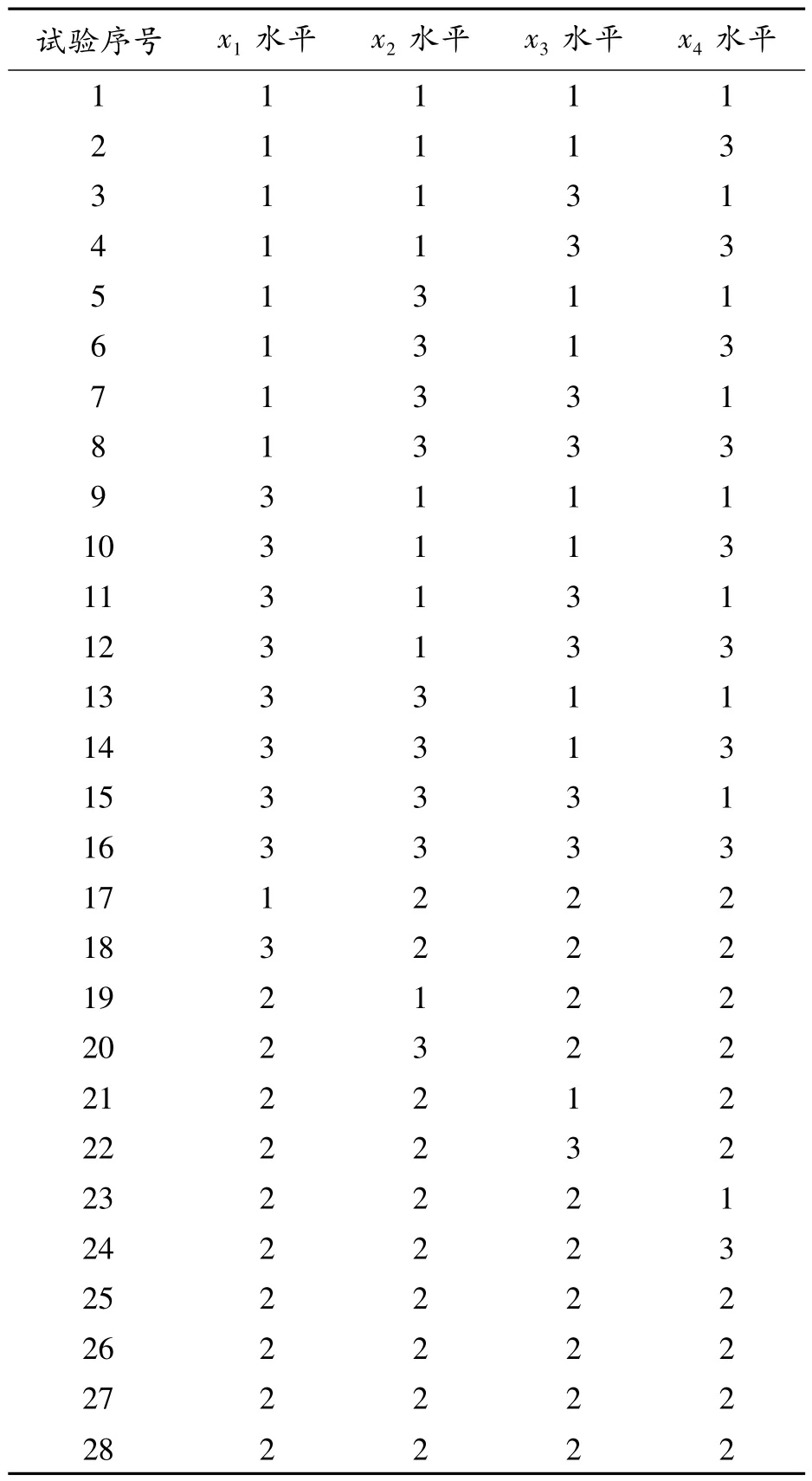
表4 试验设计

3.2 最速操纵稳定性仿真分析

在ADAMS 中建立了如图2 所示的标准双移线试验车道。路面类型选择2d 平路面，附着系数为0.8，车辆进入车道的初始车速为108 km/h。

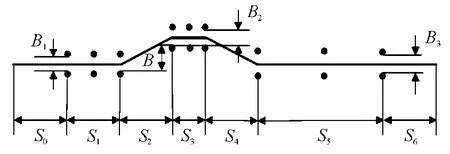
图2 双移线试验场地示意图

图2 中参数值为:

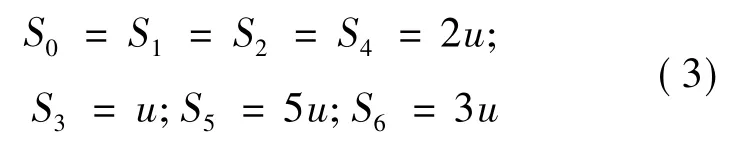
式中:u 为汽车行驶速度，m/s;S0～S6为标桩距离，m。

变道距离B=3.5 m，车宽L=1.7 m。

车道宽度为:

B1=1.1L+0.25=2.12 m

B2=1.2L+0.25=2.29 m

B3=1.3L+0.25=2.46 m

根据表4 对模型中的设计变量进行修改，利用ADAMS 软件进行28 次双移线仿真试验，得出相应的仿真结果，在Matlab 中对仿真结果进行数据处理，得到最速操纵稳定综合评价指标曲线，如图3。

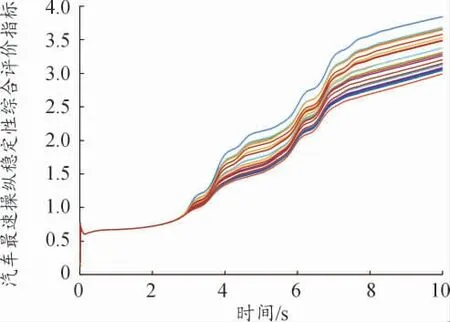
图3 最速操纵稳定性综合评价指标曲线

图3 中不同的仿真数据以不同的曲线表示。可以看出，综合评价指标受优化变量的影响较大。

3.3 建立二阶响应面模型

综合评价指标响应值和4 个设计变量之间的响应面二次多项式模型，如式(2)所示。

综合评价指标随时间不断累加，故28 次仿真试验结束时刻的综合评价指标值作为本研究响应面模型中的响应值。根据响应值和设计变量范围，采用改进过的粒子群算法拟合式(2)，设置种群粒子数目为6 000;2 个学习因子均为2;最大惯性权重因子为1，最小惯性权重因子为0.4;最大迭代次数为30。

完成二次多项式响应面模型的建立，30 次迭代后，响应面模型二次多项式为:

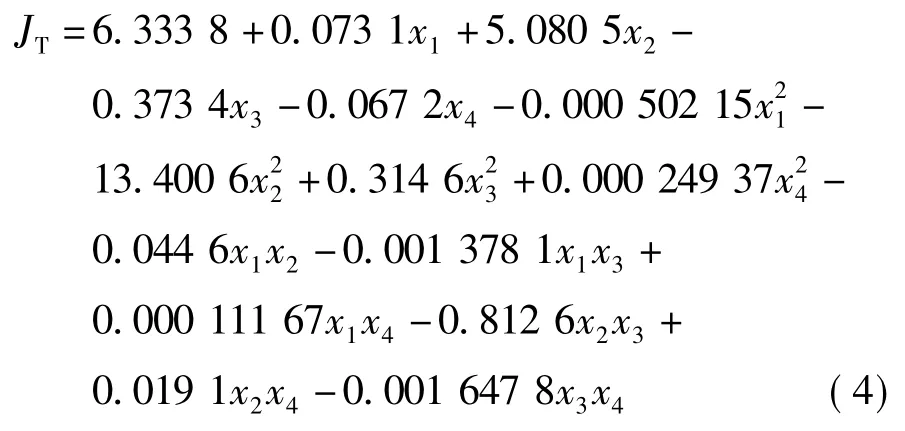
3.4 拟合模型检验

采用决定系数R-squared 检验响应面模型的拟合情况，其值在0～1。R-squared 越接近1，说明响应面模型对数据的拟合程度越高，响应面模型越准确。

式中:R2为决定系数;SST 为离差平方和;SSE 为误差平方和。

式中:yi为第i 试验的试验值;为yi的平均值。

式中:yi为第i 试验的试验值;为响应面模型计算得出的值。

计算得出响应面模型中离差平方和SST 为1.578 6，误差平方和SSE 为0.111 1，决定系数R-squared为0.929 6，接近于1，表明本研究建立的响应面模型能够较好地解释设计变量与响应之间的关系，拟合情况好。

3.5 二阶响应面模型最优解

在Matlab 中调用quadprog 函数，采用信赖域反射算法，直接在空间域中进行搜索，寻找最优解。

调用quadprog 函数需要指定响应面模型的矩阵形式，如下所示:

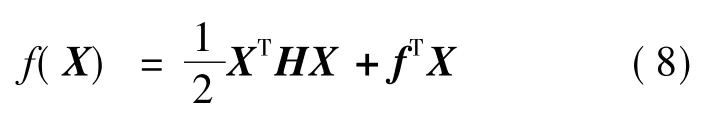
式中:X 为设计变量组成的向量;f 为响应面模型一次项系数组成的向量;H 为二次项系数组成的矩阵，如式(9)所示。

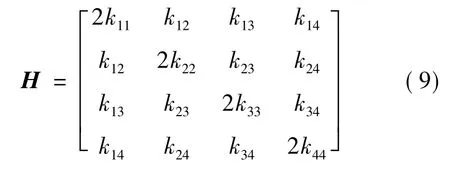
求解f(X)的最优解，最速操纵稳定性综合评价指标可通过式(10)计算得到:

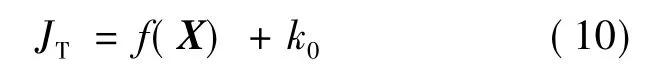
式中:k0为响应面模型的常数项。

通过quadprog 函数求解得出最优设计变量分别为:带束层帘线角度x1=25°;充气压力x2=0.28 MPa;胎面胶弹性倍数x3=1.4;带束层宽度x4=134.3 mm。

优化后的胎面胶弹性为原胎面胶yeoh 模型系数的1.4 倍，优化后的yeoh 模型系数为:C10=1.268 76，C20=-0.425 78，C30=0.115 86，D1=0.007 91。优化后的上侧带束层宽度为125.2 mm，下侧带束层宽度为143.4 mm。

4 优化结果分析

根据最优设计变量重新建立轮胎模型和对应的魔术公式轮胎模型，进行ADAMS 双移线试验仿真分析，得到各评价指标。各评价指标数值越小，则车辆相关性能越好。图4—10 为轮胎优化前和优化后的各项评价指标曲线。

1)驾驶员负担总评价指标

驾驶员负担总评价指标综合考虑了驾驶员的忙碌程度和沉重程度，如图4 所示，优化后，驾驶员负担总指标由4.694 减小到3.233，下降31.12%。说明优化后，整体驾驶员负担变低。

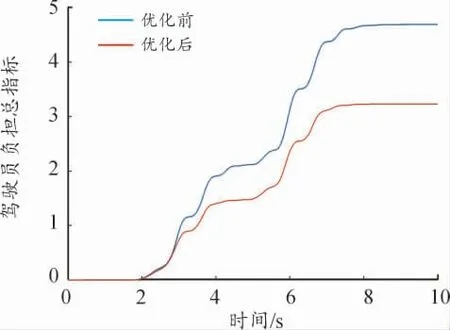
图4 驾驶员负担总评价指标优化前后曲线

2)轮胎抓地能力评价指标

轮胎抓地能力评价指标综合考虑了轮胎外倾角和轮胎附着率的影响。如图5 所示，优化后，轮胎抓地能力评价指标由2.720 减小到2.685，下降1.29%。说明优化后轮胎抓地能力有较小的改善。

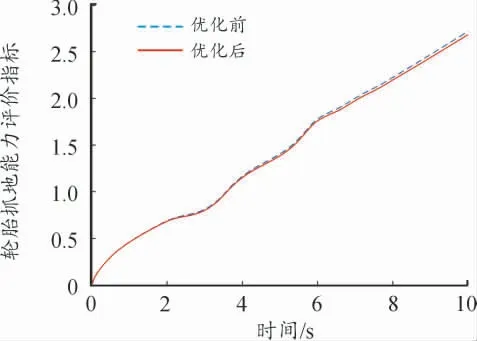
图5 轮胎抓地能力评价指标优化前后曲线

3)侧翻危险评价指标

侧翻危险评价指标综合考虑了汽车侧向加速度和汽车侧倾角的影响。如图6 所示，优化后，侧翻危险评价指标由2.220 减小到2.202，下降0.77%。说明侧翻危险评价指标优化结果不显著。

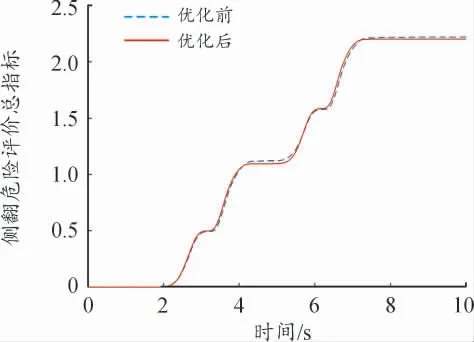
图6 侧翻危险评价指标优化前后曲线

4)侧滑危险评价指标

侧滑危险评价总指标综合考虑前后轮侧滑危险性，选取每一时刻前后轴中侧滑危险程度较大的轴的评价指标作为侧滑危险评价总指标。如图7 所示，优化后，侧滑危险评价总指标由2.446 减小到2.274，下降7.03%。说明优化后，侧滑危险程度变低。

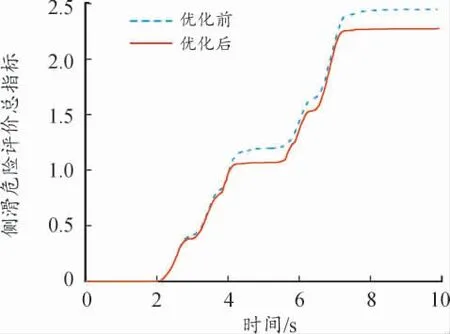
图7 侧滑危险评价指标优化前后曲线

5)响应性评价指标

响应性评价指标是通过油门开度变化及汽车纵向加速度反应汽车的响应能力。如图8 所示，优化后，汽车响应性评价指标由0.836 6 增加到0.837 1，变化极小。说明轮胎优化的设计变量对汽车响应性影响很小。

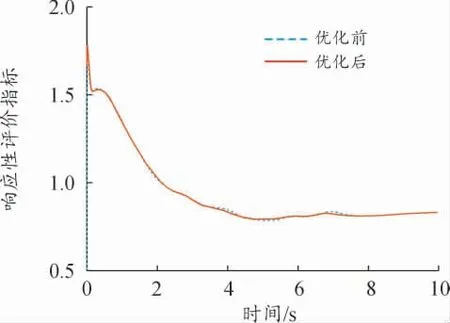
图8 响应性评价指标优化前后曲线

6)动力性评价指标

动力性总评价指标综合考虑了汽车速度和纵向加速度。如图9 所示，优化后，动力性总评价指标由4.149 3 增加到4.149 9，变化极小。说明轮胎优化的设计变量对汽车动力性影响很小。

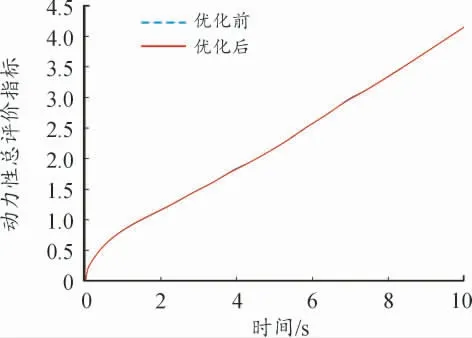
图9 动力性总评价指标优化前后曲线

7)最速操纵稳定性综合评价指标

最速操纵稳定性综合评价指标综合考虑了上述所有评价指标，如图10 所示，优化后，最速操纵稳定性综合评价指标由3.149 减小到2.836，下降9.94%。说明优化后，汽车最速操纵稳定性得到改善。

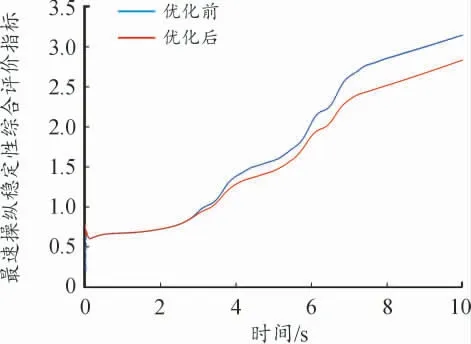
图10 最速操纵稳定性综合评价指标优化前后曲线

优化前与优化后的各评价指标如表5 所示。

表5 优化前后各评价指标

因此，驾驶员负担总评价指标和侧滑危险评价总指标都得到较为显著的优化。其中，驾驶员负担总评价指标的减小主要是由于胎面胶弹性和带束层角度的优化导致汽车转向盘转角速度减小，从而使驾驶员忙碌程度降低;侧滑危险评价总指标的减小主要是由于胎面胶弹性的优化导致轮胎侧向力与载荷的比值减小。由于轮胎优化的设计变量对汽车速度、侧向加速度、纵向加速度及轮胎附着率影响很小，导致侧翻危险评价指标、动力性评价指标、轮胎抓地能力评价指标、响应性评价指标优化结果不显著。但总体来说，汽车最速操纵稳定性综合性能得到了明显改善。

5 结论

1)驾驶员负担总评价指标和侧滑危险总评价指标都得到较为显著的优化。其中，驾驶员负担总评价指标由4.694 减小到3.233，下降了31.12%，主要是因为胎面胶弹性和带束层角度的优化导致汽车转向盘转角速度减小，从而使驾驶员忙碌程度降低;侧滑危险总评价指标由2.446减小到2.274，下降了7.03%，主要是因为胎面胶弹性的优化导致侧向力与载荷的比值减小。

2)轮胎抓地能力评价指标、侧翻危险评价指标、响应性评价指标、动力性评价指标优化结果不显著，主要是因为轮胎优化的设计变量对汽车速度、侧向加速度、纵向加速度及轮胎附着率影响很小。

3)最速操纵稳定性综合评价指标由3.149 减小到2.836，下降了9.94%，优化结果显著，说明优化后汽车最速操纵稳定性得到改善，验证了本文优化设计的可靠性，对今后轮胎的设计具有一定的参考价值。

以轮胎设计参数为优化变量，依据相关文献选择了较为保守的变量范围，仅从汽车最速操纵稳定性方面进行优化，并未充分考虑优化后的轮胎对汽车平顺性能、轮胎耐磨性能、轮胎噪音等其他性能的影响，有待进一步完善。