一类非线性系统的全局定性分析
吕海炜,蒋 凤
(1.西华大学 理学院,四川 成都 610039;2.成都大学 计算机学院,四川 成都 610106)
形如
(1)
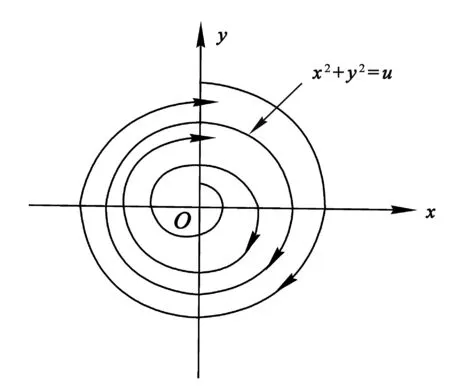
的一类二阶非线性系统[1],一些文献[2-3]只对其极限环的存在性进行了证明,但未对极限环[4]的唯一性和位置进行说明,本文不仅对极限环的存在唯一性[5]和位置进行详细说明,还讨论了随参数u变化,系统的平衡点[6]和无穷远点[7]的情况,最后用相图[8]来描述不同情况下系统的轨线走向.
1 系统(1)的平衡点分析
定理1:当u≤0时,(0,0)是系统(1)稳定的焦点;当u>0时,(0,0)是系统(1)不稳定的焦点,如图1所示.
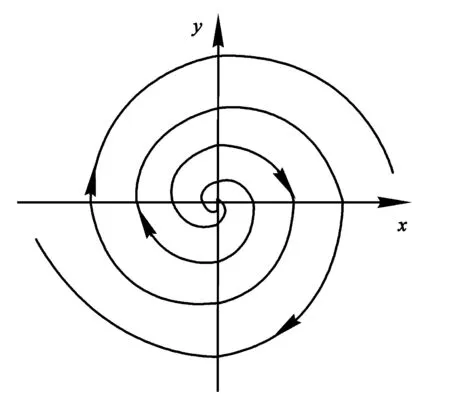
图1 u>0时系统(1)的轨线图
由平衡点的定义:
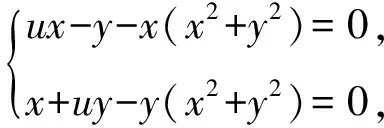
得(0,0)是非线性系统(1)的平衡点,舍去方程(1)中非线性项,得到一个常系数线性方程:
(2)
其特征方程为
λ2-2uλ+u2+1=0.
解得其特征值为
λ1=u+i,
λ2=u-i.
1)当u<0时,λ1,λ2为有负实部的虚数,所以平衡点(0,0)是系统(1)稳定的焦点.
2)当u>0时,λ1,λ2为有正实部的虚数,所以平衡点(0,0)是系统(1)不稳定的焦点.
3)当u=0时,λ1=i,λ2=-i为纯虚数,系统(2)以(0,0)为中心,此时(1)就变成
(3)
用后继函数法研究此非线性方程组在(0,0)的稳定性:
在方程组(3)中,令x=rcosθ,y=rsinθ,有
得:
继而得:
(4)
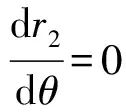
所以
r(θ,c)=c-θc3+r4(θ)c4+…,
r(2π,c)-r(0,c)=c-2πc3+r4(2π)c4+…-c-0·c3-r4(0)c4+…=
-2πc3+….
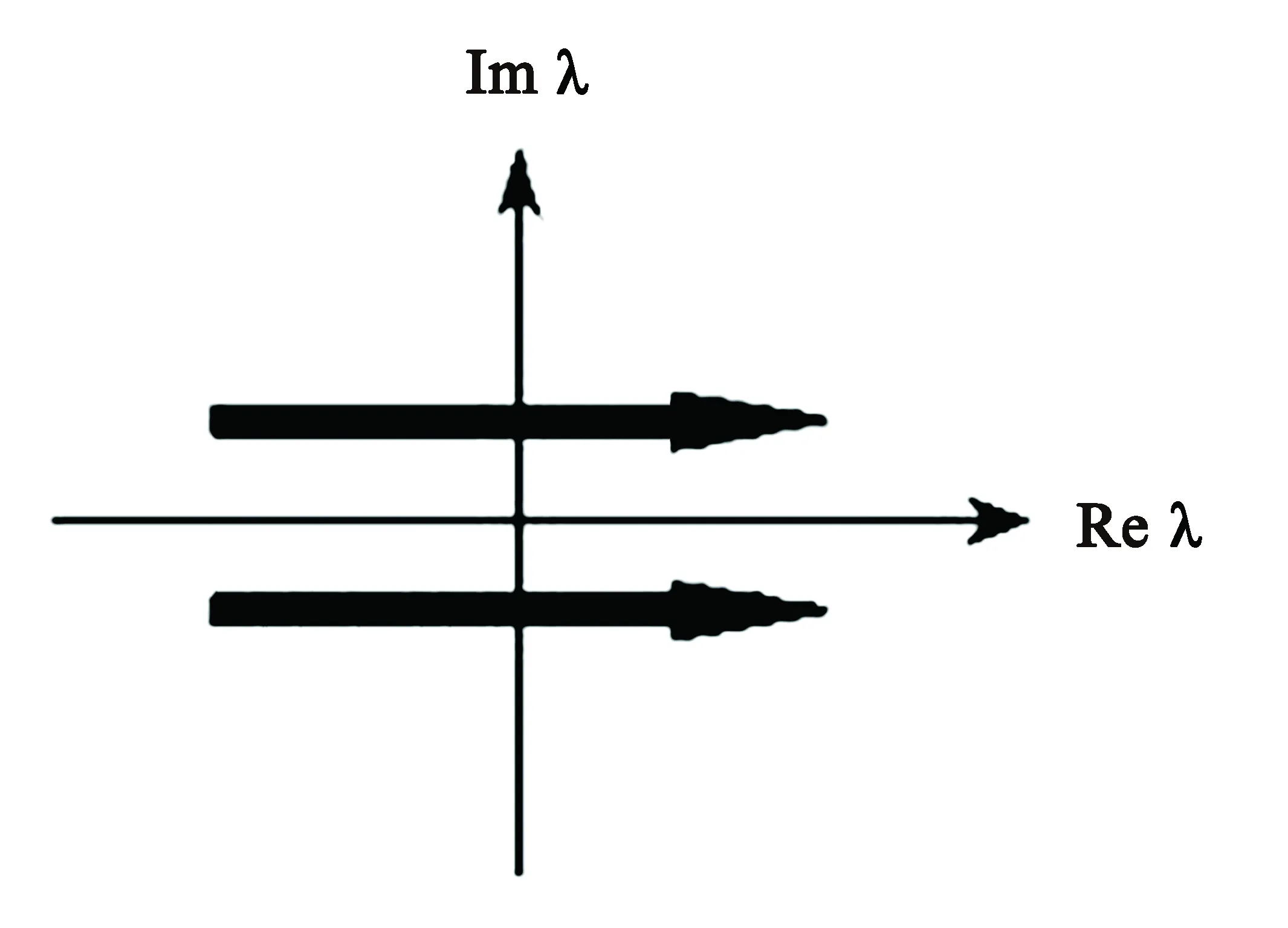
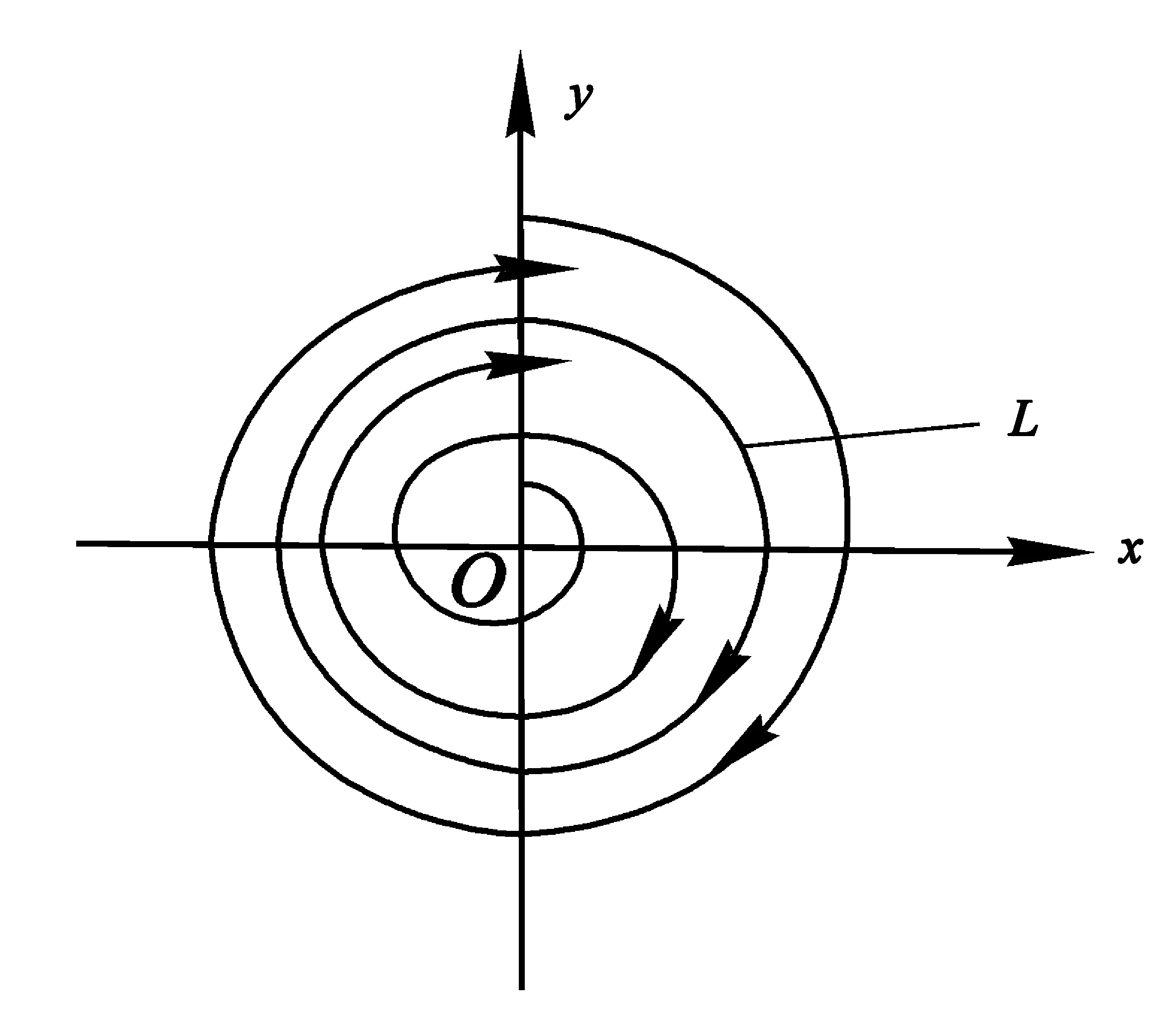
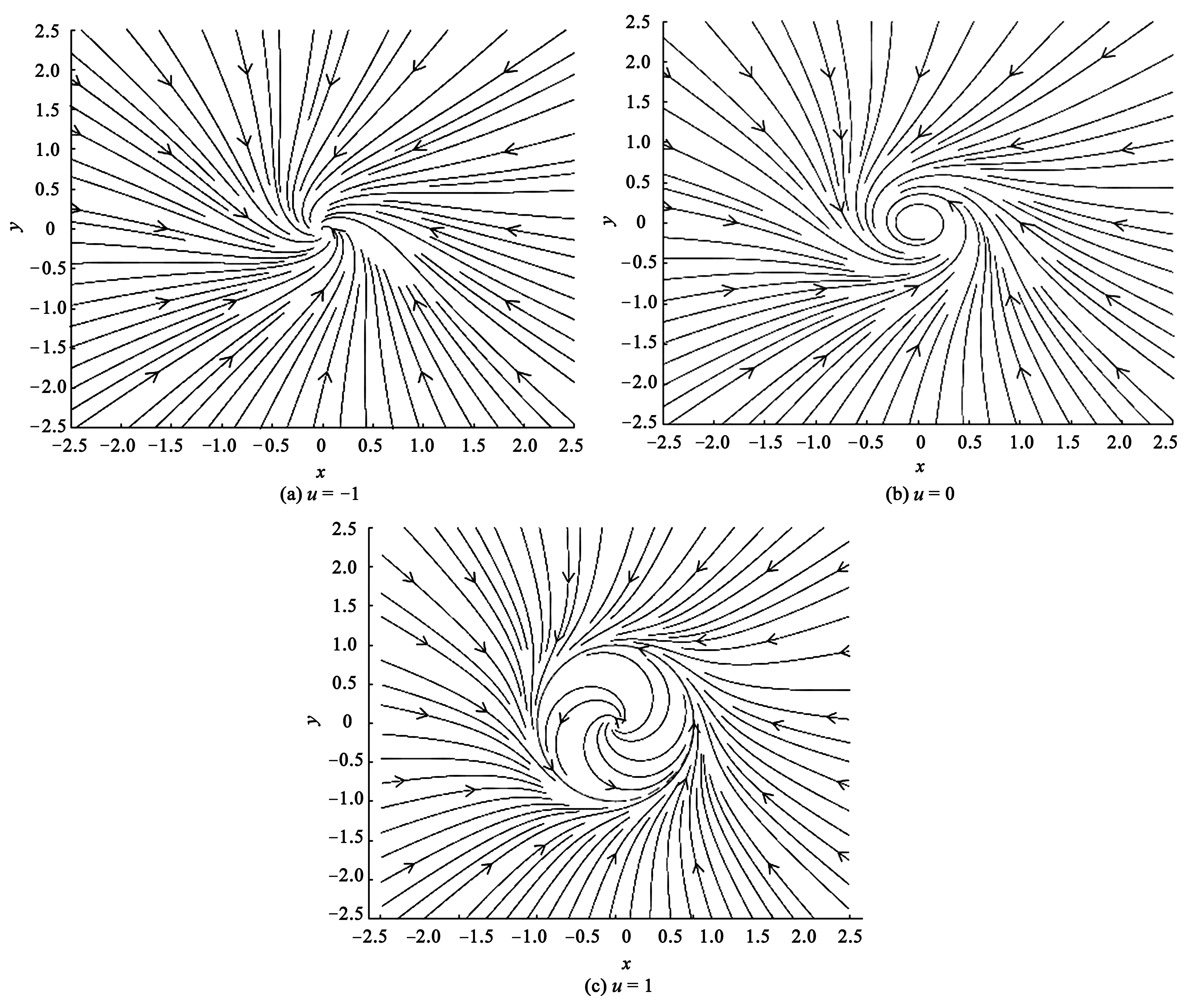
当c充分小时,r(2π,c)-r(0,c)<0⟹r(2π,c) 显然,当参数u由负变到正时,λ沿实轴上方或下方穿过虚轴,平衡点由稳定的焦点(u<0)变为不稳定的焦点(u>0),这个系统在u=0处发生了Hopf分叉[9],如图3所示. 图2 u≤0时系统(1)的轨线图 图3 Hopf分叉 事实上,该系统不只发生了奇点分叉,还发生了闭轨分叉. 上面的第二个方程表示轨线以角速度ω=1旋转,而对第一个方程,有: 1)当u≤0时,只有唯一奇点(0,0),且是稳定的焦点. 该系统的超临界分岔如图4所示. 图4 超临界分岔 定理2:当u>0时,系统存在一个稳定的极限环. 下面先讨论系统(1)在全平面上极限环的存在情况: 取H(x,y)=Exm+Fyn+Gxpyqelx+gy HP=Euxm+1-Exmy-Exm+3-Exm+1y2+Fuxyn-Fyn+1-Fx3yn-Fxyn+2+ [Guxp+1yq-Gxpyq+1-Gxp+3yq-Gxp+1yq+2]elx+gy HQ=Exm+1+Euxmy-Exm+2y-Exmy3+Fxyn+Fuyn+1-Fx2yn+1-Fyn+3+ [Gxp+1yq+Guxpyq+1-Gxp+2yq+1-Gxpyq+3]elx+gy 1)令E=G=0,F>0,则 Fu(n+2)yn-F(n+4)yn+2-F(n+4)x2yn+Fnxyn-1, 取n=-2,F=1,H(x,y)=y-2, 由Dulac判别法[10]可知,系统(1)在一、三象限不存在闭轨. 2)令F=G=0,E>0,则 取m=-2,E=1,H(x,y)=x-2, 同样的由Dulac判别法可知,系统(1)在二、四象限不存在闭轨.又因为x=0与y=0不是系统的轨线,则当u>0时,系统(1)可能存在与x轴,y轴相交的轨线. 下面用环域定理[6]来证明当u>0时,系统(1)极限环的存在性: 记V(x,y)=x2+y2,则在轨线上有 取内外境界线分别为L1和L2: 又有 故系统(1)的轨线当t增加时均由内境界线L1的内部跑向外部,由外境界线L2的外部跑向内部. 系统(1)的轨线均进入由L1和L2所围成的环域D中,在环域D中存在闭轨L,其相对位置是L1⊂L⊂L2.又因P(x,y),Q(x,y)都是解析函数,故闭轨L为稳定的极限环,如图5所示. 图5 极限环L 下面证明系统(1)存在唯一稳定的极限环: 用文献[4]中的定理6.1和定理6.8来分别证明系统(1)只存在一个极限环. 由前面可知系统(1)的极坐标形式为: 取 最后有 因为u>0,故由文献[4]中定理6.1可知系统(1)的极限环唯一. 对于系统(1) 有 P(x,y)Q(λx,λy)-P(λx,λy)Q(x,y)=[ux-y-x(x2+y2)][λx+λuy-λ3y(x2+y2)]- 对于任意的λ>1,恒有 P(x,y)Q(λx,λy)-P(λx,λy)Q(x,y)≥0, 并且只有取(0,0)点时等号成立,故由文献[4]中定理6.8可知系统(1)的极限环唯一. 下面考虑系统(1)在无穷远的情况: 1)作Poincare′变换. 即 把系统(1)变成系统 (5) (6) 2)求出系统(6)在p轴(z=0)上的平衡点,并判断其稳定性. 令z=0,则有 所以方程无实数解,则赤道上无其他奇点. 3)作Poincare′变换. 即 系统(1)化为 (7) (8) 求出系统(8)在ν轴(z=0)上的平衡点,令z=0,有 则方程也无实数解. 综上,系统(1)没有无穷远点. 由前文对系统(1)的平衡点、极限环以及无穷远点部分的推征,可大致画出系统的全局相图,如图6所示.可以清晰地看到系统存在一个平衡点(0,0),以及一个稳定极限环. 图6 系统的全局相图 利用Matlab 作图验证理论部分的准确性.图7(a)~(c)分别表示u=-1,0,1时系统(1)的全局相图. 图7 系统(1)的全局相图 通过以上对系统的平衡点随参数变化而发生变化和极限环的存在情况,以及系统在无穷远处的轨线情况,清晰了解参数取不同值时系统的轨线走向及趋势.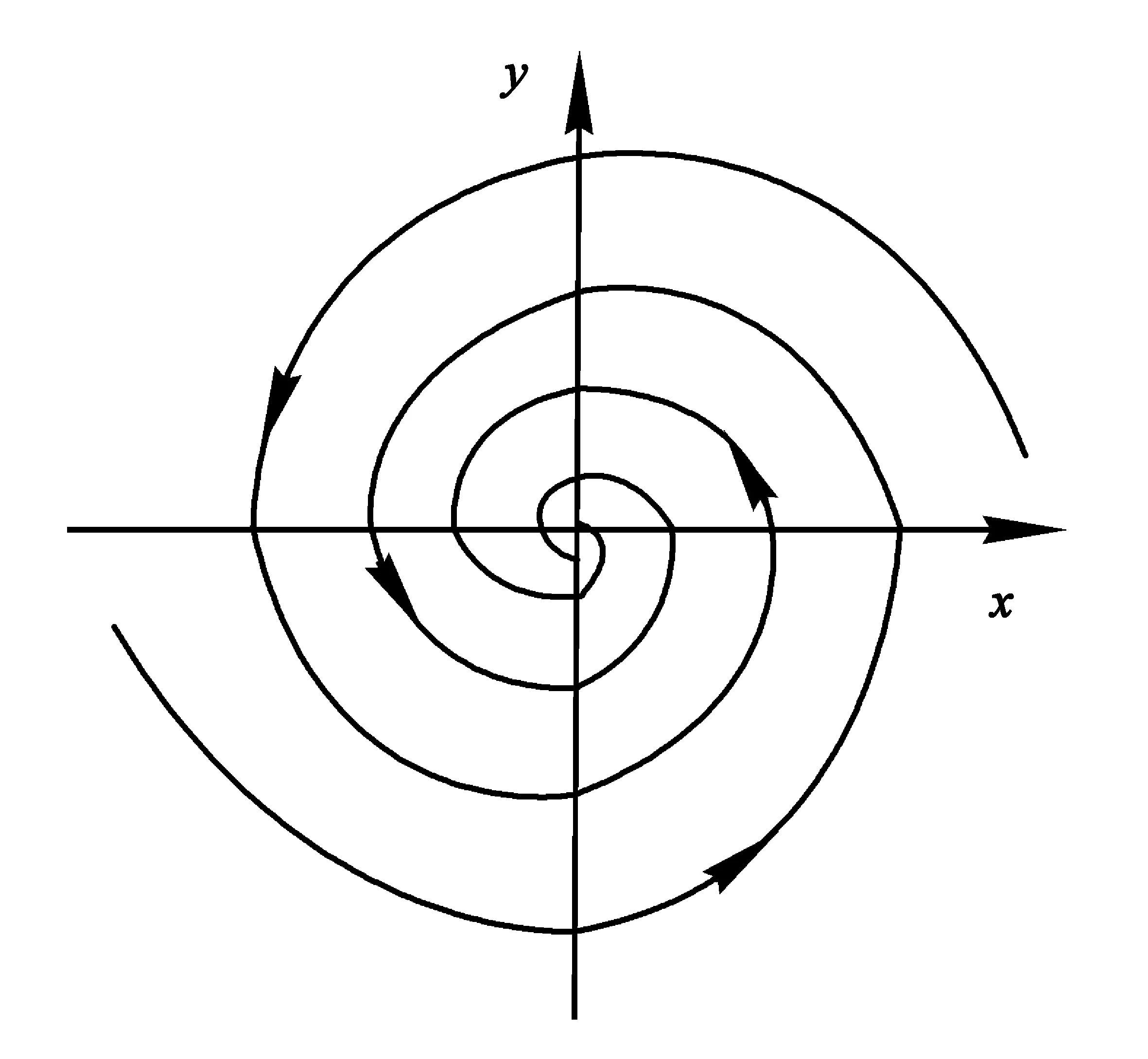
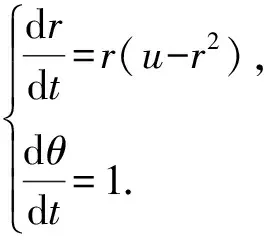

2 系统(1)存在一个稳定的极限环情况

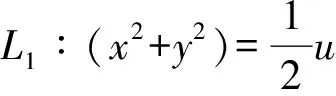
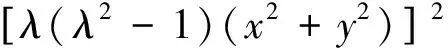
3 系统(1)在无穷远处的轨线情况
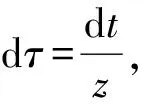
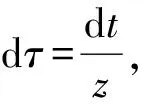
4 系统的全局相图
5 Matlab作图
6 结论

