面向轴孔类零件圆度误差评定的改进式最小区域圆法
宋 慈 焦 黎 王西彬 刘志兵 陈 晖
北京理工大学机械与车辆学院,北京,100081
0 引言
随着现代装备制造业的高速发展,高精度轴孔类零件被广泛应用于航空、船舶、冶金和汽车等各个领域,其加工质量将对产品的几何精度、疲劳极限和稳定性等诸多方面产生巨大影响。圆度是研究圆柱度、同轴度等其他形状误差的基础以及评价轴孔类零件加工质量的重要技术指标。对于发动机气缸等应用于严格轴孔配合场合的轴孔类零件,其圆度变化会导致轴孔配合不紧密,降低能量转换效率;对于冶金辊子等非配合件,孔圆度变化会使冷却道形状不规则,造成其表面温度分布不均匀,影响辊子的冷却性能。因此,对轴孔类零件的圆度进行可靠测量与精准评定,是确保零件精度要求的重要基础。
轴孔类零件的圆度误差的测量过程实际上是使用测量设备获取被测截面实际轮廓信息的过程。随着传感、光电、电磁、图像等技术的快速发展,众多学者和商业公司开发出了多种适用于圆度测量的高精度测量设备,如三坐标测量机、声发射测头[1]、电容测头[2]、光电二极管[3]、激光传感器[4-6]和CCD相机[7]等。这些新兴技术和测量设备的出现确保了轴孔类零件圆度测量过程可以高效、精确地进行。
对测量得到的点集进行误差评定是获得形状误差数值的关键。面向同一组测量数据,使用不同的误差评定方法会得到不同的评定结果,然而,当前大多数测量系统配备的误差评定算法并不足以提供精确的误差值。评定方法精度不足会将合格零件误判为不合格零件,进而影响生产效率,加大制造成本。制造精密化的目标使得全制造业对误差评定方法的精度要求越来越高,因此,开发符合误差定义的、高精度的评定方法是误差评定领域的研究重点。
圆度误差评定的4种基本方法是:最小二乘圆(least squares circle, LSC)法、最小外接圆(minimum circumscribed circle, MCC)法、最大内接圆(maximum inscribed circle, MIC)法与最小区域圆(minimum zone circle, MZC)法。四种方法中,没有任何一种方法具有通用性,不同的数据点集都有其适用的方法[8]。从误差定义符合程度看,最小区域圆法是最优的评定准则,但最小区域的构建并没有统一的方法,例如:LI等[9-11]提出最小区域线的概念,并将其作为最小区域圆的控制线;GADELMAWLA[12]通过建立凸包,利用圆弧半径的大小关系依次去除测量点集中的无效点,在剩余的点集中循环搜索,搜索出了MZC的控制点;LEI等[13]在最小二乘圆心附近设置圆形区域,利用提出的极坐标变换算法(PCTA),得到MZC中心点;GOCH等[14]利用改进切比雪夫算法逼近几何元素,得到了最大内接单元和最小外接单元。但是总体来看,多数方法仍然存在计算过程复杂、效率低、最小区域不准确以及精度不足等问题。
为此,本文提出了一种面向轴孔类零件圆度误差评定的改进式最小区域圆法。本文根据文献[15]MCC、MIC与MZC 3种方法的控制点相互联系的研究,将最小区域的求解问题转换为MCC和MIC控制点的确定问题。通常来讲,MCC和MIC控制点的求解分别需要构造外凸包点集和内凸包点集[8],以简化计算量、获取符合要求的测量点。但该构造过程极其复杂,特别是内凸包点集的“不唯一性”会对评定结果造成很大的不确定性。本文所提出的方法以测量点间的距离为判定依据,遵循多边形去除法则,在无需求解凸包点集的情况下,精准地确定MCC和MIC控制点,进而得到测量点集的最小区域。
1 圆度误差评定
圆度是指回转体零件某一横截面的实际被测轮廓与其理想轮廓的变动量,即工件截面趋近圆的程度。圆度误差指同一截面上包容被测轮廓的两个最小同心圆的半径之差[16]。如图1所示,Mc为实际被测轮廓,Zc为最小包络同心圆,其半径差f即为圆度误差。因此,圆度误差评定的过程就是求解参考圆及其圆心的过程[17]。
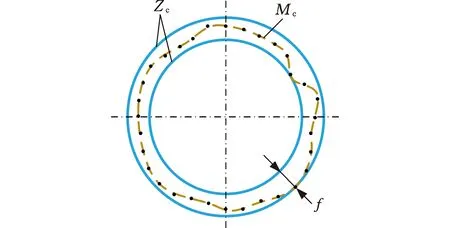
图1 圆度误差示意图Fig.1 Schematic diagram of roundness error
1.1 改进式最小区域圆法
最小区域圆法以测量点集的最小区域圆的圆心来评定圆度误差。测量点集的最小区域圆指满足以下条件的两个同心圆:①所有测量点都在两同心圆上或在两者之间;②两同心圆半径差最小。其判定准则为:由两同心圆包容测量点集时,至少有内、外相间的四点与同心圆接触,并且外圆上两点连线与内圆上两点连线相交,称为相交准则。根据最小外接圆、最大内接圆与最小区域圆之间的关系[15],最小区域圆的控制点可通过最小外接圆与最大内接圆的控制点进行求解。
最小外接圆和最大内接圆的构建过程遵循锐角三角形或对径准则,即:在求解圆上有三点与测量点集接触,该三点组成锐角三角形;或只有两点与测量点集接触,此时两点的中点为求解圆的圆心。因此,最小区域圆的两个外控制点可以从最小外接圆的控制点中选取,两个内控制点可以从最大内接圆的控制点中选取。
1.2 最小区域圆法评定圆度误差的评定过程
1.2.1确定最小外接圆控制点
对于给定测量点集Pi(xi,yi),i=1,2,…,n,按下式计算点集的中心点Ooch(xoch,yoch):
(1)
依次计算点集Pi中各点与Ooch的距离,得到与Ooch相距最远的点P1,连接直线P1Ooch;分别搜索该直线两侧与直线距离最大的点P2和P3,对应距离分别为d1max和d2max,如图2a所示。点P2、P3与P1共同组成一个三角形,按下式判断所构成三角形是否为钝角三角形:
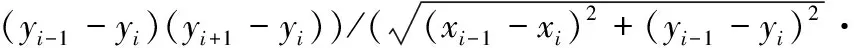
(2)
若为钝角三角形,则以三角形最长边为直径、最长边的中点为圆心作外接圆。如果所作外接圆包容凸包点集,那么所作外接圆为测量点集的最小外接圆;如果所作外接圆不能包容凸包点集,那么求解最长边两侧与其相距最远的两点,与最长边构成四边形。在四边形中,依次计算过相邻三点的圆弧半径,去除最大圆弧半径值对应的点,构成新三角形。重复上述步骤,直至所构成的三角形外接圆能包容凸包点集,此时所作外接圆即为测量点集的最小外接圆。
若为锐角三角形,则按下式计算经过三点的外接圆的圆心O′(cx,cy)与半径Rr:
(3)
A=x1(y2-y3)-y1(x2-x3)+x2y3-x3y2
如果所作外接圆包容凸包点集,那么所作外接圆为测量点集的最小外接圆;如果所作外接圆不能包容凸包点集,那么求解与圆心最远距离的点,并与三角形三个顶点组成四边形。如图2b所示,某次计算过程中,△P1P2P3为锐角三角形且有测量点在所作外接圆外部,则搜索与圆心距离最大的点P4,对应距离为dismax。P4和△P1P2P3三个顶点构成四边形P1P2P4P3,如图2c所示。在四边形中,依次计算相邻三点的圆弧半径,去除最大圆弧半径值对应的点,构成新三角形。重复上述步骤,直至所构成的三角形外接圆能包容凸包点集,此时所作外接圆即为测量点集的最小外接圆,圆心为Omcc,半径为rmcc。
所求最小外接圆对应的三角形顶点P′1、P′2和P′3即为最小外接圆的控制点,如图2d所示。
1.2.2确定最大内接圆控制点
对于同样一个测量点集Pi(xi,yi),i=1,2,…,n,按式(2)计算测量点集的中心点Op,依次求解点集中各点与Op的距离,得到与Op距离最小的点P5,连接直线P5Op。然后,分别搜索该直线两侧与直线距离最小的点P6和P7,对应距离分别为d1min和d2min,如图3a所示,与点P5共同组成三角形。按式(2)判断所构成三角形是否为钝角三角形。
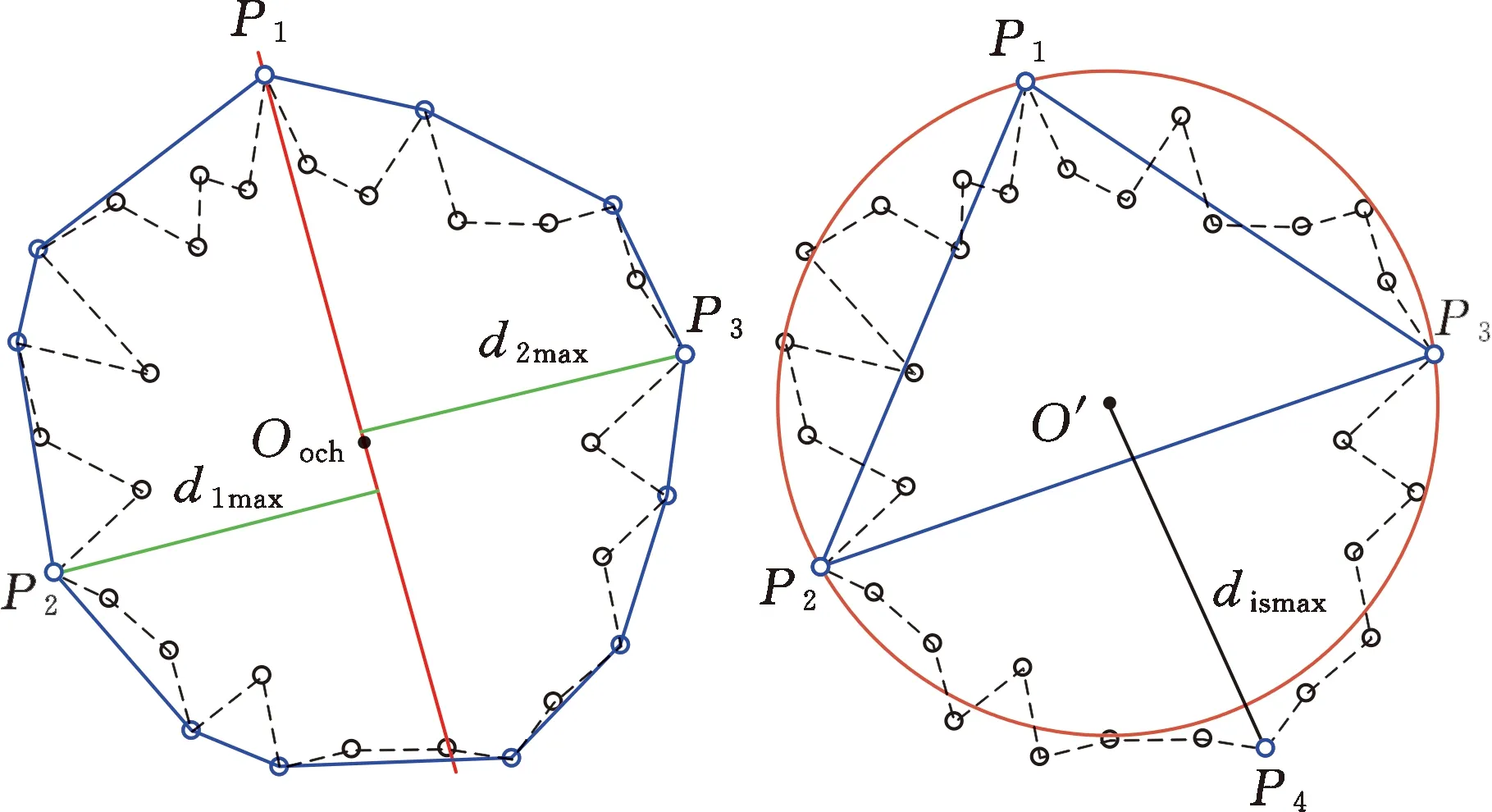
(a)搜索P1Ooch两侧与其距离最大点P2和P3(b)搜索与外接圆圆心O′距离最大点P4
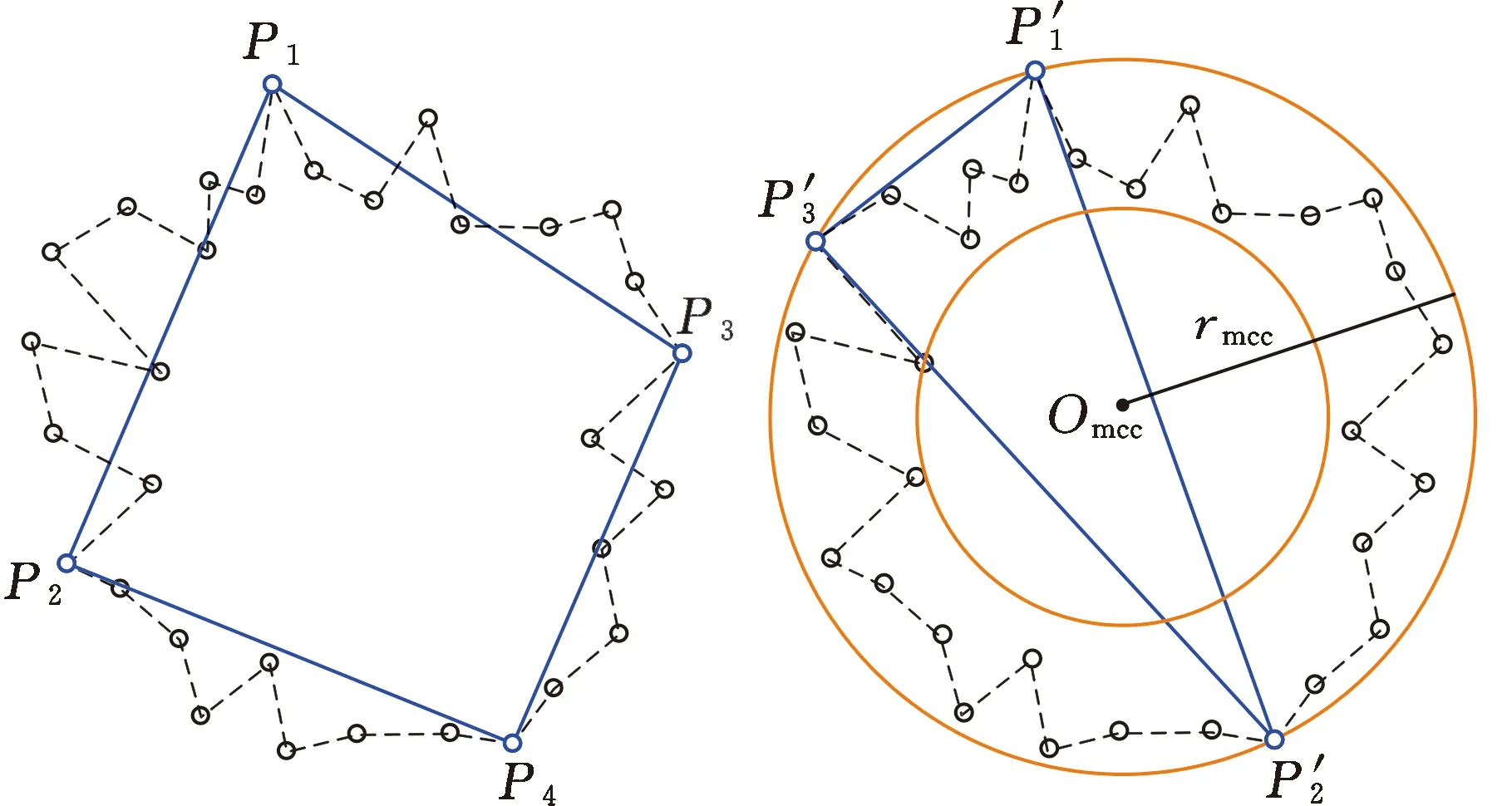
(c)将点P4加入三角形组成四边形(d)最小外接圆的控制点P′1、P′2和P′3图2 最小外接圆控制点的搜索过程Fig.2 Search process of control points of minimumcircumscribed circle
若为钝角三角形,则以三角形最长边为直径、最长边的中点为圆心作外接圆。如果所有测量点均在所作外接圆上或外部,那么所作外接圆为测量点集的最大内接圆;如果有测量点在所作外接圆内部,那么求解最长边两侧与其距离最小的两点,与最长边两点构成四边形。如图3b所示,某次计算过程中,△P5P6P8为钝角三角形且有测量点在所作外接圆内部,则求解最长边P6P8两侧与其距离最小的两点P5和P9,对应距离分别为dis3min和dis4min。点P5和P9与最长边P6P8构成四边形P5P6P9P8,如图3c所示。在四边形中,依次计算过相邻三点的圆弧半径,去除最小圆弧半径值对应的点,构成新三角形。重复上述步骤,直至所有测量点均在所构成的三角形外接圆上或外部,此时所作外接圆即为测量点集的最大内接圆,圆心为Omic,半径为rmic。
若为锐角三角形,则按式(3)计算经过三点的外接圆的圆心与半径。如果所有测量点均在所作外接圆上或外部,那么所作外接圆为测量点集的最大内接圆;如果有测量点在所作外接圆内部,那么求解与圆心距离最小的点,与三角形三个顶点组成四边形。依次计算四边形相邻三点的圆弧半径,去除最小圆弧半径值对应的点,构成新三角形。重复上述步骤,直至所有测量点均在所构成的三角形外接圆上或外部,此时所作外接圆即为测量点集的最大内接圆。
所求最大内接圆对应的三角形顶点P″1、P″2和P″3即为最大内接圆的控制点,如图3d所示。
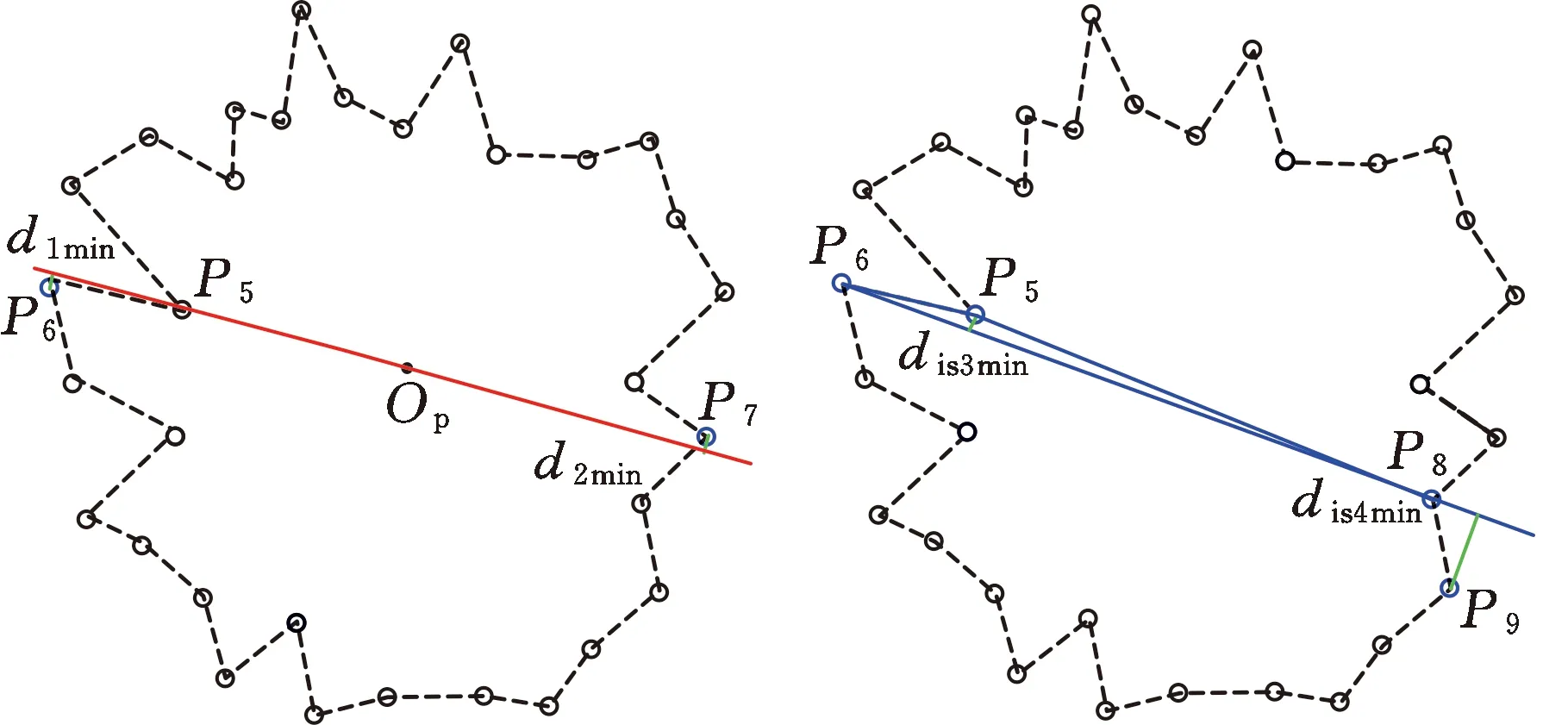
(a)搜索P5Op两侧与其距离最小的点P6和P7(b)搜索最长边P6P8两侧与其距离最小点P5和P9

(c)点P5、P6与P9、P8构成四边形(d)最大内接圆的控制点P″1、P″2和P″3图3 最大内接圆控制点的搜索过程Fig.3 Search process of control points of maximuminscribed circle
1.2.3确定最小区域圆控制点
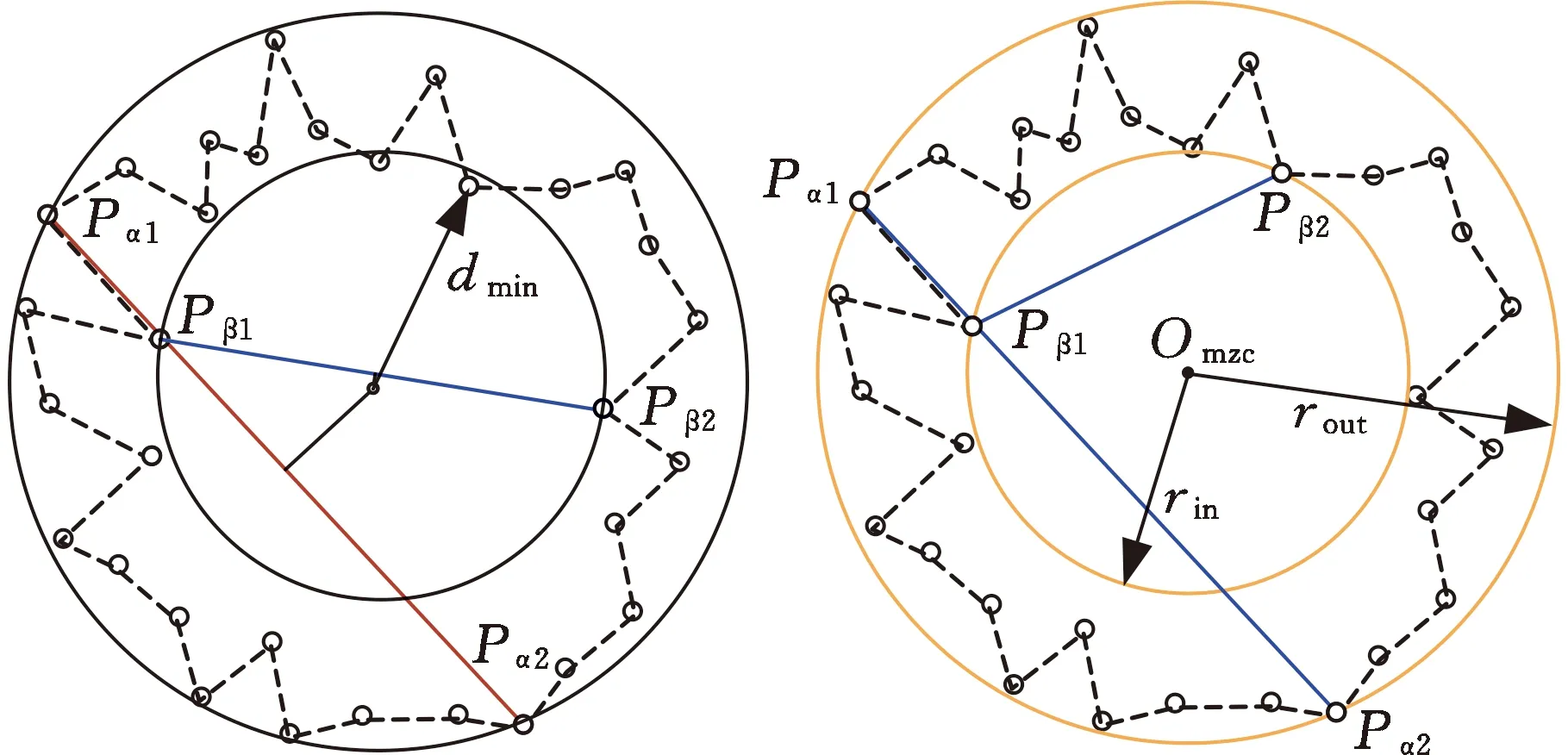
如图4a所示,对于点集Pi(xi,yi),i=1,2,…,n,将最小外接圆控制点P′1、P′2、P′3存入外控制点集Cmax中,将最大内接圆控制点P″1、P″2、P″3存入内控制点集Cmin中,从Cmax与Cmin中各任意选择两点构建同心圆。
设每次从Cmax中选择的点坐标为Pα1(x1,y1),Pα2(x2,y2),从Cmin中选择的点坐标为Pβ1(x3,y3),Pβ2(x4,y4)。按下式计算同心圆圆心坐标(xx,yy):
(4)
其中,k1为直线Pα1Pα2的斜率;k2为直线Pβ1Pβ2的斜率;x1mid、y1mid分别为点Pα1与Pα2中点的横坐标和纵坐标;x2mid、y2mid分别为点Pβ1和Pβ2中点的横坐标和纵坐标。
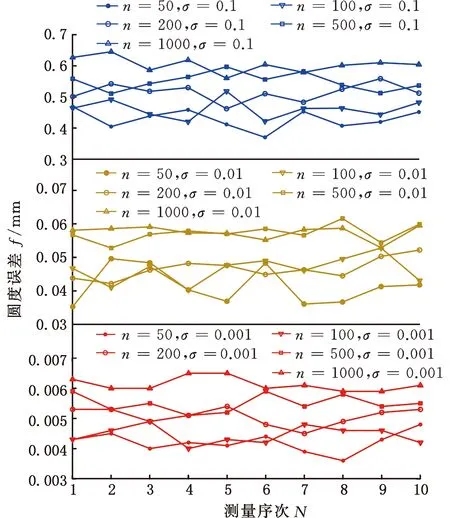
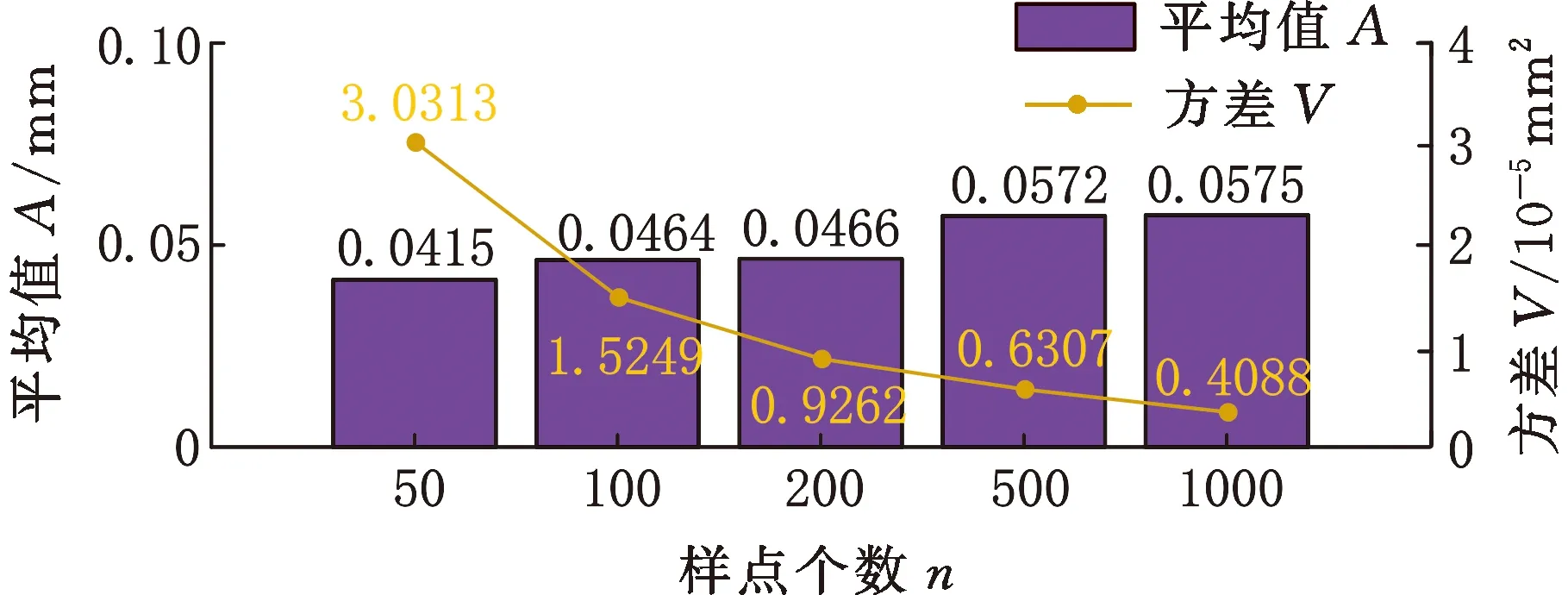
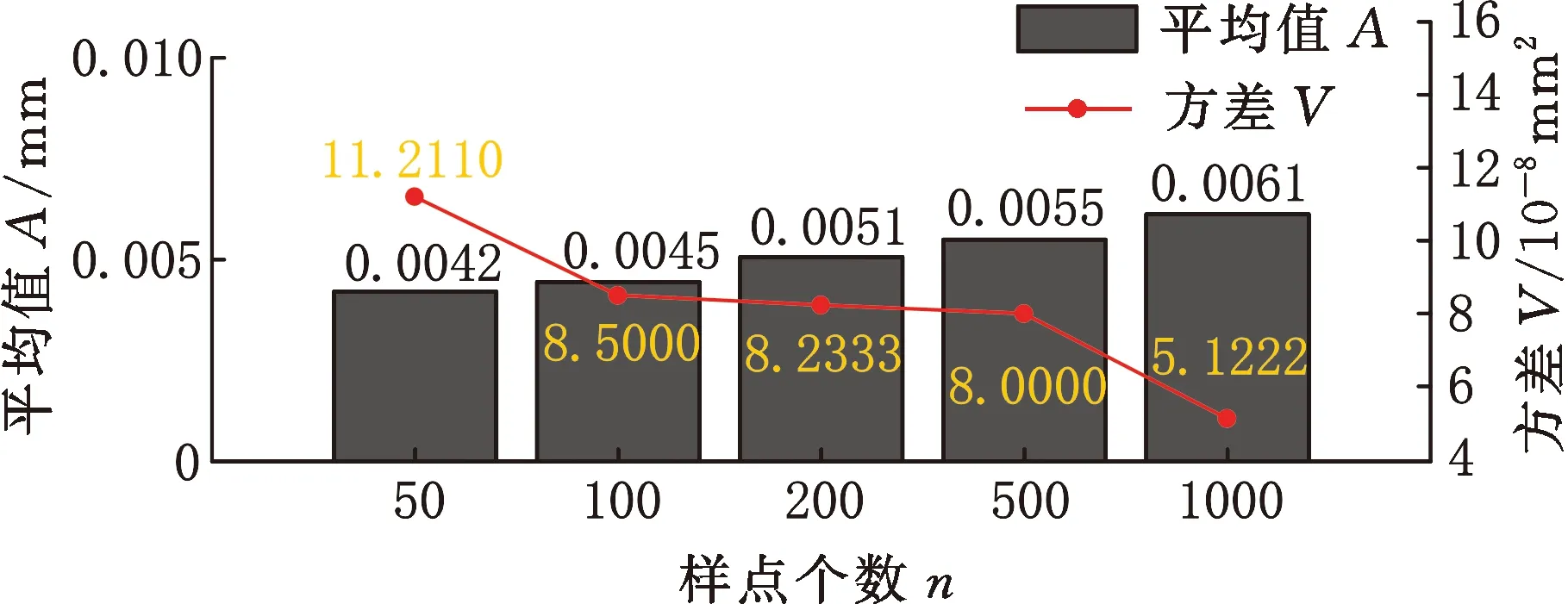
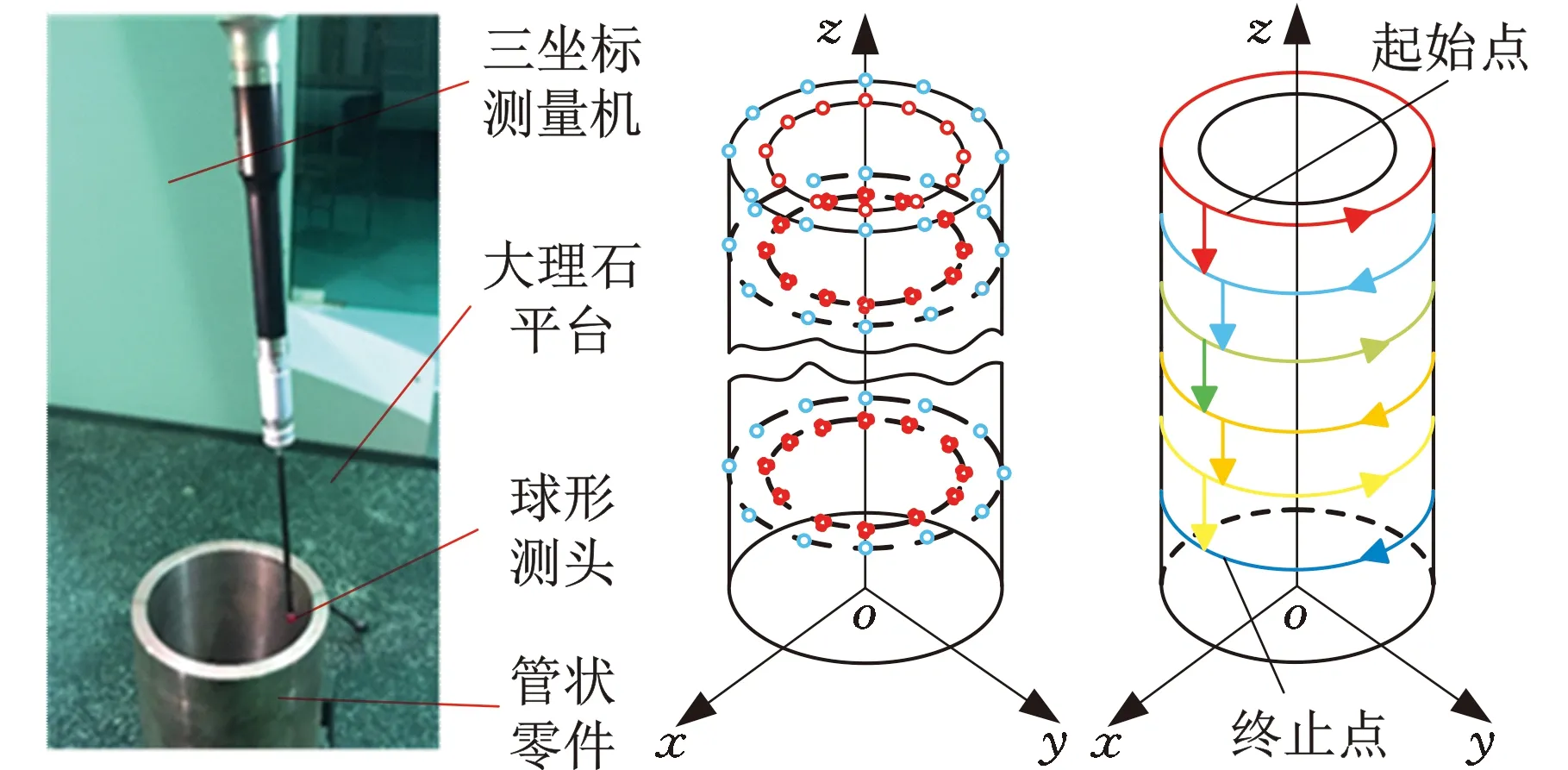
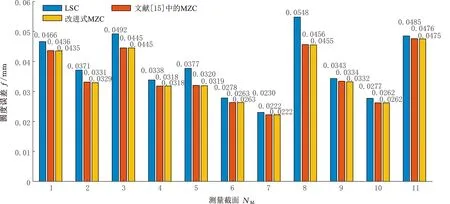
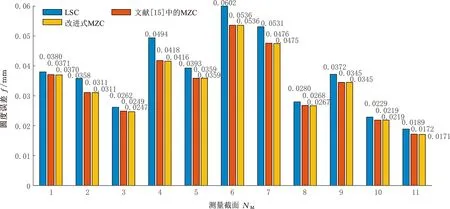
计算每种情况下构建的两同心圆能否包容Cmax与Cmin中所有的测量点。如图4b所示,当构建的两同心圆可以包容全部Cmax与Cmin中的测量点时,选择半径差最小的两同心圆对应的Pα1、Pα2、Pβ1与Pβ2进行后续计算。将Pα1、Pα2存入点集Dmax中,Pβ1、Pβ2存入Dmin中。计算同心圆的半径rout、rin与测量点集Pi(xi,yi)中各点到同心圆圆心的距离di。如图4c所示,若dmax>rout,则dmax对应的测量点加入Dmax中;若dmin (a)内外控制点集 (b)包容内外控制点 (c)dmin对应测点加入Dmin (d)圆度误差评定图4 最小区域圆控制点的搜索过程Fig.4 Search process of control points ofminimum zone circle 1.2.4误差评定 最小区域圆法评定的圆度误差 fmzc=rout-rin (5) 为验证所提出的MCC和MIC控制点求解方法以及MZC控制点构建模式的有效性与准确性,分别使用LSC、优化的MCC、优化的MIC和改进式MZC等方法对文献[15]中表3、表5和表7的点集数据进行评定,结果如图5~图7所示。 图5 文献[15]中表3数据评定结果Fig.5 Evaluation results of tab.3 in literature [15] 图6 文献[15]中表5数据评定结果Fig.6 Evaluation results of tab.5 in literature [15] 图7 文献[15]中表7数据评定结果Fig.7 Evaluation results of tab.7 in literature [15] 最小二乘圆有2个控制点,最小外接圆有3个控制点,最大内接圆有3个控制点,最小区域圆有4个控制点。该结果与理论相符,LSC法需要内、外2个极限距离的控制点,MCC与MIC法需要3个(或2个)顶点构建最小外接圆或最大内接圆,MZC法需要内、外各2个控制点确定同心圆。 对于MCC和MIC法,优化前后获得的误差值基本保持一致;在面向某些点集数据时,优化后的方法甚至获得了更小的误差值。更小的误差评定值对应的评定方法被视作更好的方法,这是因为该方法获得了更小的符合圆度误差定义的最小区域。因此,优化后的方法在求解MCC和MIC控制点方面展现出了更好的竞争力。同样地,与文献[15]中的MZC法相比,使用本文提出的改进式最小区域圆法获得了相同或更小的误差值,这意味着该方法在测量截面上搜索到了更好的最小区域。由此表明,构建MZC控制点的模式以及搜索得到的最小区域圆是有效的。 轴孔类零件圆度误差的获取分为数据测量和数据评定两个过程。改进式最小区域圆法每一步搜索得到的几何值均为确定极值,因此,在面向同一测量数据点集时,由该评定方法计算的误差结果具有唯一性。然而,由于数据测量过程具有不可避免的随机误差,因此在对某一确定测量截面进行采样时,每次获得的数据点集在空间中的分布情况都是不同的。最小区域圆定义为包络所有数据点集的两个最小同心圆,这导致所有基于最小区域圆原理的误差评定方法均会受到样点分布情况的影响。换言之,测量数据的随机误差会给评定结果造成一定的不确定性,使其在一定数值范围内波动。 为探究测量数据的随机误差对评定结果的影响规律,在MATLAB 2018b软件平台上对直径100 mm的理想圆线进行离散化处理,分别获得n为50、100、200、500和1000个理想离散数据点,并依次对不同数量的数据点集引入均值为0、标准差σ为0.1、0.01或0.001的正态分布随机变量,以模拟测量数据的随机误差。在某一样点数量和某一标准差的状态下,连续运行10次,获取10组不同的数据点集,使用改进式最小区域圆法进行误差评定,评定结果如图8所示。分别对10组误差结果进行统计学分析,平均值A和方差V如图9所示。 图8 误差评定结果Fig.8 Evaluation results of errors (a)σ=0.1 (b)σ=0.01 (c)σ=0.001图9 误差结果的平均值和方差Fig.9 Average and variance of error results 随机误差的标准差主要取决于采样设备的测量精度。在相同的标准差下,样点个数的增加会使误差结果的方差减小;在相同的样点个数下,随机误差标准差的减小会使误差结果的平均值显著减小。这说明,通过增加采样点个数以及提高测量设备精度的方式,可以有效降低随机误差对误差测量、评定过程的影响。 由于本文提出的圆度误差评定方法是面向轴孔类零件的,故使用Hexagon Global Advantage三坐标测量机对管状零件的内外表面进行测量,并分别将其内外表面的测量样点作为孔、轴类零件直线度误差评定的数据基础。该三坐标测量机行程范围为500 mm×700 mm×500 mm,测量精度为(2.5+3.0L/1000)μm,其中L为测量范围。测量环境温度为20 ℃,相对湿度为70%,无冷凝,供气压力为0.5 MPa。采用的测头型号为TIP2BY球形,其校正误差为0.0008 mm。对内径85 mm、外径100 mm、高200 mm的管状零件的下底面做磨削处理,以保证该底面具有较好的平面度。然后,将零件置于三坐标测量机的大理石平台上,以其下底面为oxy平面,构建测量坐标系,采样现场如图10a所示。如图10b所示,在零件内外表面沿z轴方向等间距确定11个测量截面,在每个测量截面进行等间隔采样。采样路径如图10c所示,遵循路径最短原则,保证测量效率。 (a)采样现场 (b)采样模式 (c)采样路径图10 测量实验示意图Fig.10 Schematic diagram of measurement experiment 分别使用LSC方法、文献[15]中的MZC方法与改进式MZC方法对管状零件内外表面的圆度误差进行评定,评定结果见图11与图12。 图11 内表面圆度误差评定结果Fig.11 Evaluation results of roundness errors of inner surface 图12 外表面圆度误差评定结果Fig.12 Evaluation results of roundness errors of outer surface 可以看出,相较于最小二乘圆法,最小区域圆法在处理不同数据时,均能保持最优的评定精度,这主要是由于后者最符合圆度误差标准中的最小区域原则。而与文献[15]中的MZC法相比,改进式最小区域圆法均获得了相同或更小的误差值,具有更好的评定精度。这说明改进式最小区域圆法适用于轴孔类零件圆度误差的评定过程,且具有良好的准确性。 由式(5)可知,改进式最小区域圆法计算得到的圆度误差可进一步表示为 (6) 其中,(xout,yout)、(xin,yin)分别为位于最小区域圆上的外控制点、内控制点。 根据GPS标准给出的不确定度理论[18],确定圆度误差模型中各元素(xout、yout、xin、yin、xx、yy)的不确定度、传递系数以及彼此间的相关系数,是求解圆度误差值不确定度的基础。各元素的传递系数由误差值对各元素的偏导数表示,则圆度误差的不确定度uf为 (7) 其中,u0、ux、uy、uxy分别为样点坐标值的单点不确定度、x向圆心坐标的不确定度、y向圆心坐标的不确定度以及x向与y向圆心坐标间的相互不确定度;ρxy为x向与y向圆心坐标间的相关性系数。 将存在相关性的参数xx和yy视作一个统计向量ξ,通过对同一次采样过程中得到的样点进行分组拟合得到其协方差矩阵Cov(ξ),该矩阵可用来表示参数的不确定度和相互不确定度[19]。在得到协方差矩阵后,还可以按下式计算获得参数间的相关性系数: (8) 测量数据的单点不确定度u0主要取决于测量设备的示值误差、重复性、温度敏感性以及测量接触力引起的变形等。由式(7)可知,圆度误差的不确定度与测量数据的单点不确定度存在正比例关系,因此,测量设备精度的提高可有效增加误差结果的可靠性。 图5~图7统计了最小二乘圆法、最小外接圆法、最大内接圆法和改进式最小区域圆法在面向相同测量数据点集时的评定时间t。最小二乘圆法计算简便,时间最短,但精度最差;而改进式最小区域圆法的搜索过程较为复杂,且时间最长,这是因为它是建立在最小外接圆法与最大内接圆法所获控制点的基础上进行求解的。但对于评定精度,最小区域圆法具有明显优势。 此外,使用改进式最小区域圆法对不同数量的点集数据进行了测试,表1所示为不同数量点集下最小区域圆法的评定时间。当点集数量为1000时,改进式最小区域圆法的评定时间也能保持在0.1 s左右,具有良好的评定效率,足以满足实际的工程需求。 表1 不同数量点集下最小区域圆法评定时间 改进式最小区域圆法基于最小区域圆原理,在评定过程中构建包络所有样点的两个最小同心圆;而最小二乘圆法是通过最小化各样点与圆心间的误差值实现的。从评定原理上分析,改进式最小区域圆法对测量数据本身的敏感性要大于最小二乘圆法,因此,在面对奇异测量点时,改进式最小区域圆法的稳健度要略低于后者。 为有效改进这一劣势,在获取测量数据点集时,基于测量设备自身的良好重复性,在某一确定测量截面上进行多次采样,去除奇异测量点,并对每个位置处的多组样点取平均值,以降低随机误差的影响,提高测量数据的准确性以及评定方法的稳健度。 针对轴孔类零件圆度误差的精准评定,本文提出了一种简单有效的改进式最小区域圆法,避免了凸包求解给评定算法造成的复杂性和不确定性。基于点间距离和多边形去除法则优化了最小外接圆控制点和最大内接圆控制点的搜索过程,最小区域圆控制点依次从两者的控制点集中进行选取,以点间距离为优化目标,逼近点集的最小区域圆。 面向同样的测量点集,相较于优化前,优化后的最小外接圆法、最大内接圆法和最小区域圆法均获得了相同或更小的误差值,搜索到了更优的目标圆线,这证明了所提出评定算法控制点的有效性。通过仿真实验分析了测量数据的随机误差对误差结果的影响,随着数据点个数的增加以及测量设备精度的提高,随机误差的影响明显降低。 最后,对管状零件内外表面圆度误差进行了测量与评定实验,研究了改进式最小区域圆法的相关特性: (1)该方法在评定精确性上展现出了与其他方法等同甚至更优的竞争力,足以在测量点集空间范围内建立更好的包络圆。 (2)算法的不确定度取决于测量设备的精度以及使用条件,测量设备精度的有效提升可以有效提高结果的可靠性。 (3)算法在面向较多数量的测量点时仍表现出了良好的评定效率,满足实际的工程使用需求。 (4)测量设备依赖自身重复性在同一位置多次采样,去除奇异点并取平均值,可以有效提高算法的稳健度。这说明了改进式最小区域圆法适用于轴孔类零件圆度误差的评定过程。
2 控制点有效性分析

3 测量数据的随机误差对误差结果的影响

4 误差测量与评定实验
5 相关特性分析
5.1 不确定度
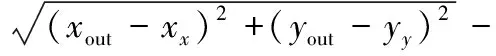
5.2 评定效率

5.3 稳健度
6 结论

