面向小样本高维数据的秩检验非参控制图

赵 宇 李艳婷

上海交通大学机械与动力工程学院，上海，200240

0 引言

统计过程控制(statistical process control，SPC)是利用数据对生产过程和产品质量进行监控的重要工具，也是贯彻实施全面质量管理的重要工具和质量保证手段。随着大数据时代的到来以及数据感知和收集技术的成熟，质量数据向着多维度高频次方向发展，多元统计过程控制(MSPC)成为了一个重要的研究问题。

随着数据量的增加，不符合传统正态性、低维度和样本充足假设的数据越来越常见，例如：半导体制造企业通过传感器技术实时收集和监控的工业生产中的关键质量指标维度超过500维[1]；生产过程稳定的电子元器件的寿命数据近似服从指数分布[2]；机械结构的疲劳寿命、磨损寿命、疲劳强度数据大多服从威布尔分布；供应商产品质量检验中常见的单侧截尾的非正态数据和双侧截尾的非正态数据等；人造卫星、运载火箭、精密数控机床等产品受生产周期、实验条件、研发成本等因素的限制，产量较少，收集到的数据十分有限；航空发动机中机匣转子的碎片击穿率评估、复合材料的许用值估计、武器射程评估等都属于小样本问题。

面向高维、非正态和小样本数据的控制图是当前多元统计过程控制研究的热门方向。ZOU等[3]基于非参数似然比检验的方法设计了一个改进的非参数EWMA控制图；李静等[4]研究了控制图参数k的动态更新和迭代，设计了监测过程方差微小波动的改进CUSUM控制图；赵春华等[5]提出了一种基于融合特征约减的KPCA-SVM控制图;BAE等[6]提出了一种基于数据深度的非参数多变量控制图；HE等[7]运用了支持向量机监控多元过程的方法，提出了一种基于距离的控制图。DENG等[8]基于实时对比的策略设计非参控制图(记为RTC控制图)；CHEN等[9]将Wilcoxon秩和检验与提出的多元经验分布检验融合，设计出的EWMA控制图对高维监控很有效(记为DFEWMA控制图)；ZOU等[10]在多元符号检验的基础上，设计了EWMA控制图(记为SREWMA控制图)；HAWKINS等[11]基于未知参数和已知参数的转化设计了具有自启动结构的EWMA控制图(记为SSEWMA控制图)；LI等[12]基于游程检验的双样本检验设计了在高维度大漂移情况下表现优异的多元非参数控制图(记为HAMEWMA控制图)。本文设计的HREWMA非参数控制图在监测高维数据的大漂移时具有非常优异的表现，因此选择上述在此条件下表现优异的多元非参控制图进行对比。QIU[13]系统地分类并总结了非参数控制图的研究进展。

针对变量相关性未知、分布未知、高维度等情况的数据监测问题，本文结合文献[14]基于高维数据秩序的双样本检验，提出了基于高维数据秩序与EWMA结合的高维非参数控制图(HREWMA)。通过马尔可夫链的方法求解HREWMA控制图的平均运行链长(ARL)，研究多种参数条件下控制图ARL的表现。对比RTC控制图[8]、DFEWMA控制图[9]、SREWMA控制图[10]、SSEWMA控制图[11]、HAMEWMA控制图[12]，证明在高维度小漂移的情况下HREWMA控制图的表现更好。

1 基于高维秩检验的非参数控制图

1.1 高维秩检验

假设Xij=(Xij1，Xij2，…，Xijp)T是相同且独立分布的观测值，i=1，2分别表示第1个、第2个样本；j=1，2,…，ni，用n=n1+n2表示总样本量，其中，n1、n2分别为样本1与样本2的样本量。N=p(n1+n2)是总样本量n对应的p个维度的全部观测值。

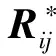
(1)

1≤rijk≤n

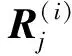
(2)

定义边际分布函数的平均值为

定义渐近秩变换为

Yij=(Yij1，Yij2，…，Yijp)T

Yijk=H(Xijk)

(3)

(4)

u∈[0,n1]v∈[1,n1]u∈Nv∈N

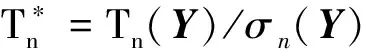
(5)

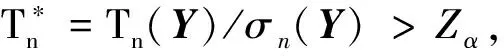
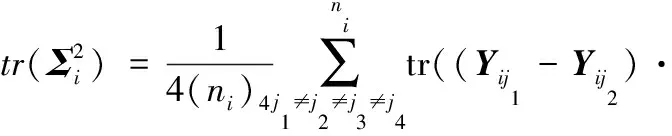
(6)

(7)

(ni)k=ni!/(ni-k)!

j1∈[1,ni]j2∈[1,ni]j3∈[1,ni]

j4∈[1,ni]j1,j2,j3,j4∈N

经过文献[14]改进的检验统计量的第一类错误概率更低，并且该检验统计量更适用于非参数假设，因此本文采用文献[14]提出的检验统计量进行EWMA控制图的设计。

1.2 多元非参数控制图HREWMA

本文秩检验的方法过程均值偏移的方向是已知的(向上漂移)，采用传统的双边EWMA控制图监控过程的效果并不理想，为了充分利用过程均值的方向信息，采用单边EWMA控制图来监控过程。设定单边EWMA控制图的统计量为

(8)

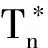
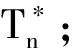
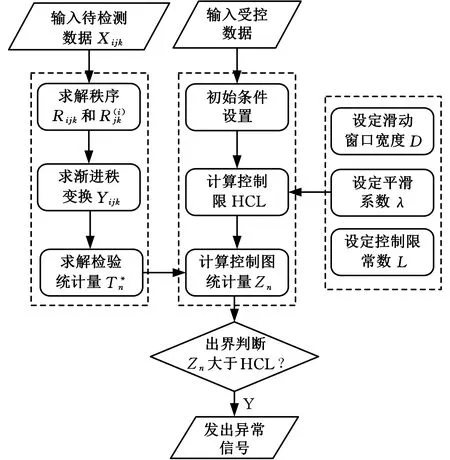
图1 HREWMA控制图的监控过程Fig.1 The monitoring process of HREWMA control chart

计算HREWMA控制图平均运行链长的方法如下：

(1)设定平滑系数λ和滑动窗口D的值；

(2)设定控制限常数L并计算控制图的控制限(n表示所计算样本的数据量)：

(9)

(3)设定HREWMA控制图检验统计量初始值Z0=0；

(4)根据式(8)求得Zn；

(5)通过马尔可夫链求解受控状态下的平均运行链长ARL，然后通过蒙特卡罗随机模拟法求解失控状态下的ARL。

1.3 HREWMA检验统计量计算的程序加速方法

针对本文检验统计量的计算，采用常规的计算方法将耗费大量的时间，因此，针对本文检验统计量的计算，尤其是针对比率一致估计σn的计算，给出以下程序加速建议。

1.3.1减少重复计算项

基于该程序加速规则，使用该方法的理论程序运行时间减少至未使用该加速方法的1/8。对于一个受控样本量m0=50、滑动窗口D=10、数据维度p=10的HREWMA控制图，使用该加速方法与未使用该加速方法相比，计算量从105数量级减小至104数量级。

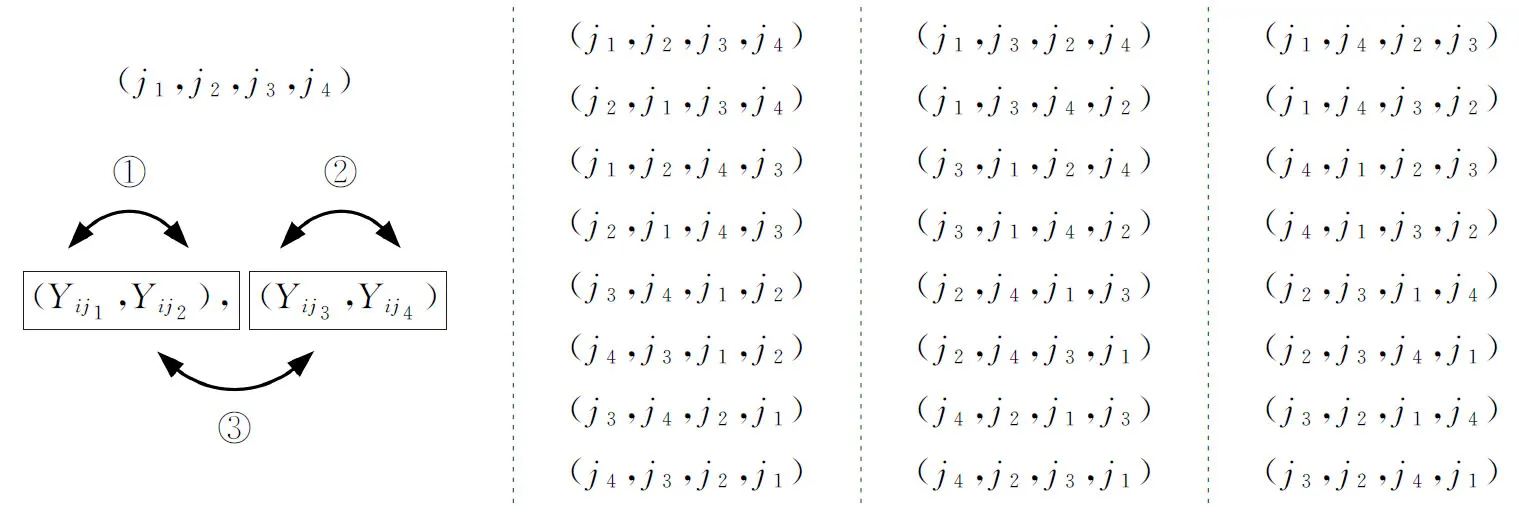
图2 检验统计量加速方法：减少重复项

1.3.2矩阵迹的加速计算

在计算式(6)时，涉及到两方阵相乘后取矩阵的迹的计算，采用常规的计算方法，需要先将两个方阵相乘后的矩阵求出，再将矩阵的对角线元素相加取迹。基于图3所示的计算方法，可以减少矩阵中行列相乘的计算次数，加快程序速度。

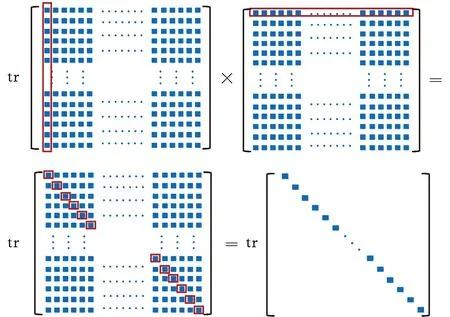
图3 检验统计量加速方法：矩阵迹的加速计算Fig.3 Test statistics acceleration method:acceleratedcalculation of matrix trace

基于该程序加速规则，使用该方法的理论程序运行时间减少至未使用该加速方法的1/p。对于一个受控样本量m0=50、滑动窗口D=10、数据维度p=10的HREWMA控制图，使用该加速方法与未使用该加速方法相比，将计算量从104数量级减小至103数量级，程序运行时间减少至未使用该加速方法的1/10。

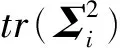
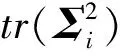
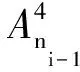
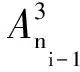
基于该程序加速规则，使用该方法的理论程序运行时间减少至未使用该加速方法的4/m0。对于一个m0=50、D=10、p=10的HREWMA控制图，使用该加速方法与未使用该加速方法相比，将计算量从103数量级减小至102数量级，程序运行时间减少至未使用该加速方法的2/25。

1.4 HREWMA控制图平均运行链长的计算

平均运行链长(ARL)表示从检测开始直到控制图发出警报所抽取的平均样本数量。当过程是受控的，为了避免误报情况的发生，希望ARL越大越好；当过程是失控的，希望控制图可以尽快报警，希望失控的ARL尽可能小。在比较不同控制图的性能时，ARL是不容忽视的指标。控制图ARL的计算方法有：蒙特卡罗随机模拟法、积分法和马氏链法。本文采用马氏链法计算HREWMA控制图的平均运行链长。

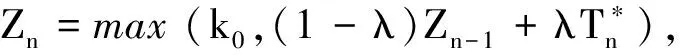
首先，对HREWMA控制图进行区间划分。将控制限区间[t0，LHCL]划分成t个子区间，每个子区间的宽度为d=(LHCL-k0)/t，此时HREWMA控制图的统计量Zn在控制限区间[t0，LHCL]的变化过程可以看作具有(t+2)个状态的马尔可夫链转移问题。

然后，定义每个区间的状态Sn，n=1，2，…,k，统计量Zn处于状态Sn的条件可以表示为

LHCL-nd≤Zn≤LHCL-(n-1)dn=1，2，…k

最后，构造出HREWMA控制图的状态转移概率矩阵

(10)

其中，pi，j代表统计量Zn从状态Si转移到状态Sj的概率。

综上可知，P是t+1阶方阵，最后一行(0，0，…，0，1)代表从吸收状态St+1到转移状态Si的概率，最后一列(v1，v2，…，vt，1)T代表从转移状态Si到吸收状态St+1的概率。可以看到，ARL的取值只受前t行的影响，因此对一步转移概率矩阵进行分块：

(11)

其中，R矩阵是将P矩阵去掉最后一行和最后一列得到的t阶矩阵，I是t阶单位矩阵，1是一个元素全是1的t×1列向量，0是一个元素全是0的t×1列向量。

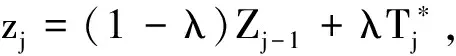
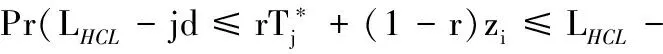
(12)

根据马尔可夫链的性质可得，第i步转移概率矩阵Pi可以表示为

(13)

因此链长LRL=i的概率：

Pr(LRL=i)=Pini(Ri-1-Ri)1

(14)

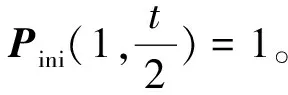
因此平均运行链长ARL可以表示为

(15)

2 仿真检验

HREWMA控制图的优势在于对高维度、大漂移数据的检测，所以选择此状况下具有优异表现的多元非参数控制图作对比：RTC控制图[8]，DFEWMA控制图[9]，SREWMA控制图[10]，SSEWMA控制图[11]，HAMEWMA控制图[12]。

2.1 仿真参数设定

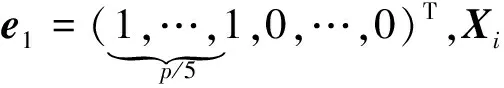
(1)HREWMA控制图平滑系数λ，分别取值0.05和0.1；

(2)受控样本数量m0分别取值50，60，70，80，90；

(3)受控样本和待检测样本的维度p分别取值10，20，30，40，50；

(4)均值漂移量δ分别取值0.5，1，2，4；

(5)滑动窗口宽度D分别取值10，20，30，40，50；

(6)检测数据的分布考虑以下3种分布类型：①多元正态分布，记作Normp；②多元t分布，自由度是ξ，记作tp，ξ，其中ξ=5；③多元Gamma分布，形状参数φ，尺寸参数是1，记作Gamp，φ，其中φ=3。

2.2 仿真结果

运用马尔可夫链得到HREWMA控制图受控状态的平均运行链长，记为IC ARL(ARL受控); 因为无法估计失控状态下检验统计量的分布情况，故通过蒙特卡罗随机模拟法求解HREWMA控制图失控状态的平均运行链长，记为OC ARL(ARL失控)。在IC ARL相同的设定下，比较不同控制图OC ARL的大小，OC ARL越小，说明控制图的性能更好。

2.2.1受控过程分析(ICARL)

在初始受控平均运行链长200的设定下，对比HREWMA控制图与一些代表性的多元非参数控制图(HAMEWMA、SREWMA、DFEWMA、SSEWMA、MSEWMA、MEWMA、RTC)在受控数据监测中的平均运行链长(IC ARL)，结果如表1所示。

由表1可知，HREWMA控制图的IC ARL大致在200左右，并且标准差也大致为200。表中的MSEWMA、MEWMA、RTC控制图的ICARL显著低于预期设定值，在实际的监控过程中会频繁报警，在受控状态下HREWMA控制图的监控效果比较稳定。

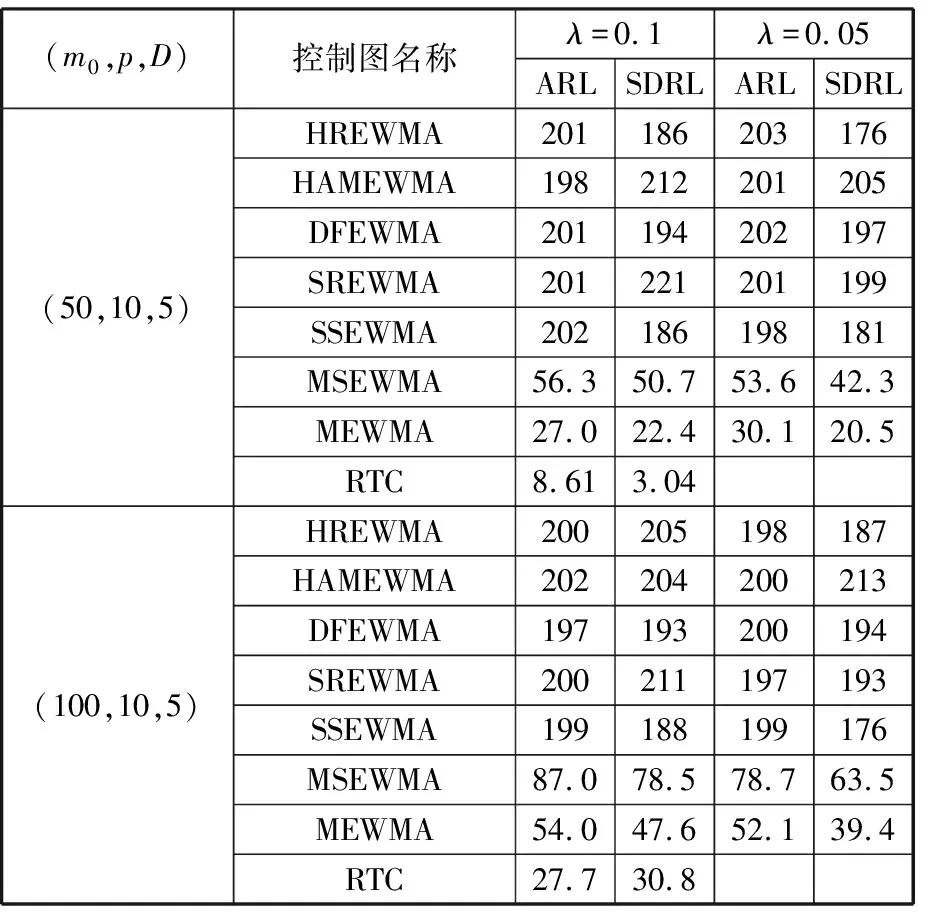
表1 控制图表现对比(IC ARL)

2.2.2失控过程分析(OCARL)

在不同分布类型、漂移量、滑动窗口宽度、数据维度、平滑系数及受控样本量的条件下，各个控制图在失控状态下的表现情况如下。

(1)滑动窗口的影响。由图5可知，随着滑动窗口的增大，3种分布的OC ARL均逐渐减小，其中，多元t分布的OC ARL减小的程度更加明显，说明滑动窗口宽度越大，HREWMA控制图的控制效果越好。

(2)数据维度的影响。由图6可知，对于多元正态分布、多元t分布、多元Gamma分布，随着数据维度的增大，OC ARL逐渐减小，数据维度越高，HREWMA控制图的控制效果越好，因此HREWMA控制图处理高维数据时有更好的表现。

(3)受控样本量的影响。由图7可知，随着受控样本量的增大，3种分布的OC ARL均逐渐减小，但是减小程度明显小于滑动窗口和数据维度的影响，证明HREWMA控制图不需要过高的受控样本量。

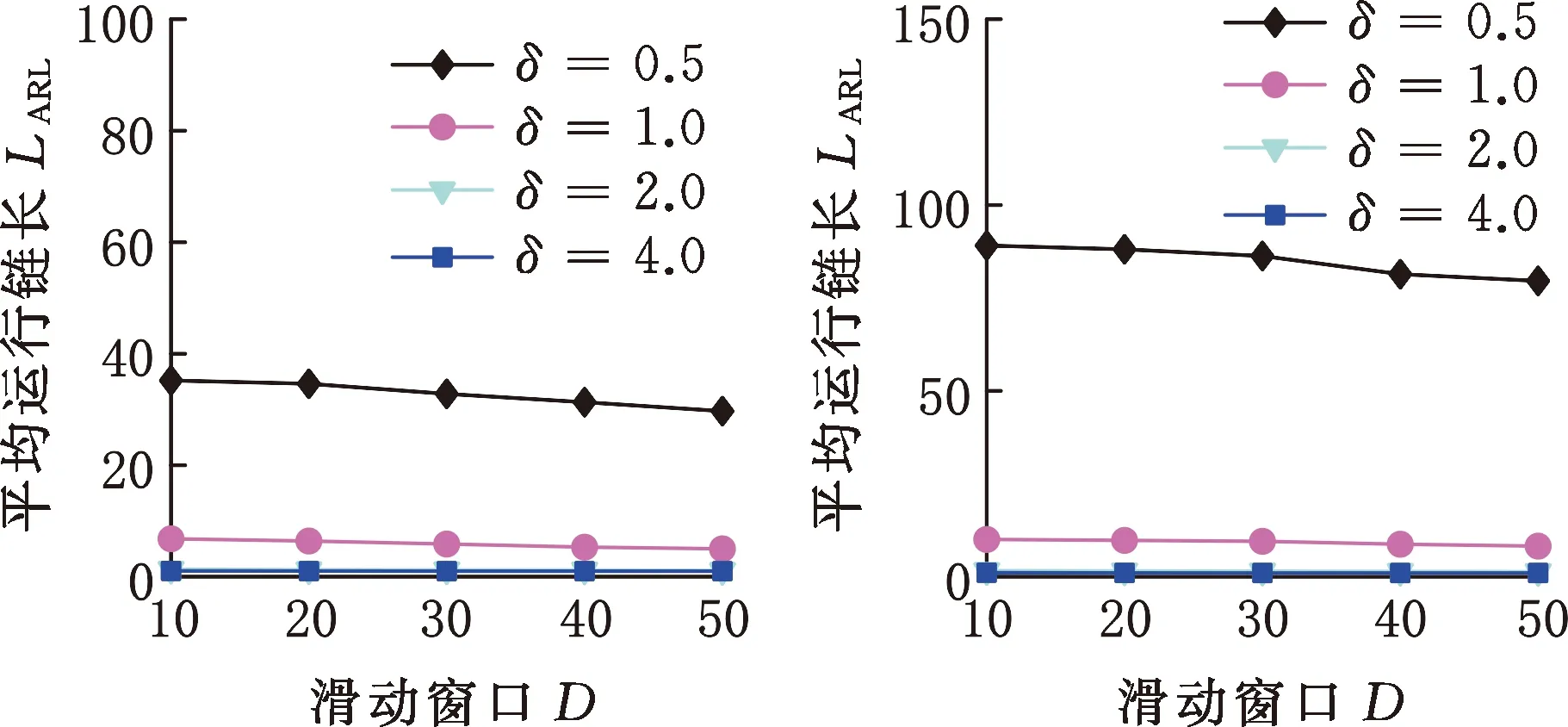
(a)Norm10 (b)t10，5

(c)Gam10，m3图5 HREWMA控制图在不同滑动窗口下的OC ARL比较Fig.5 Comparison of OC ARL of HREWMA controlchart under different sliding windows

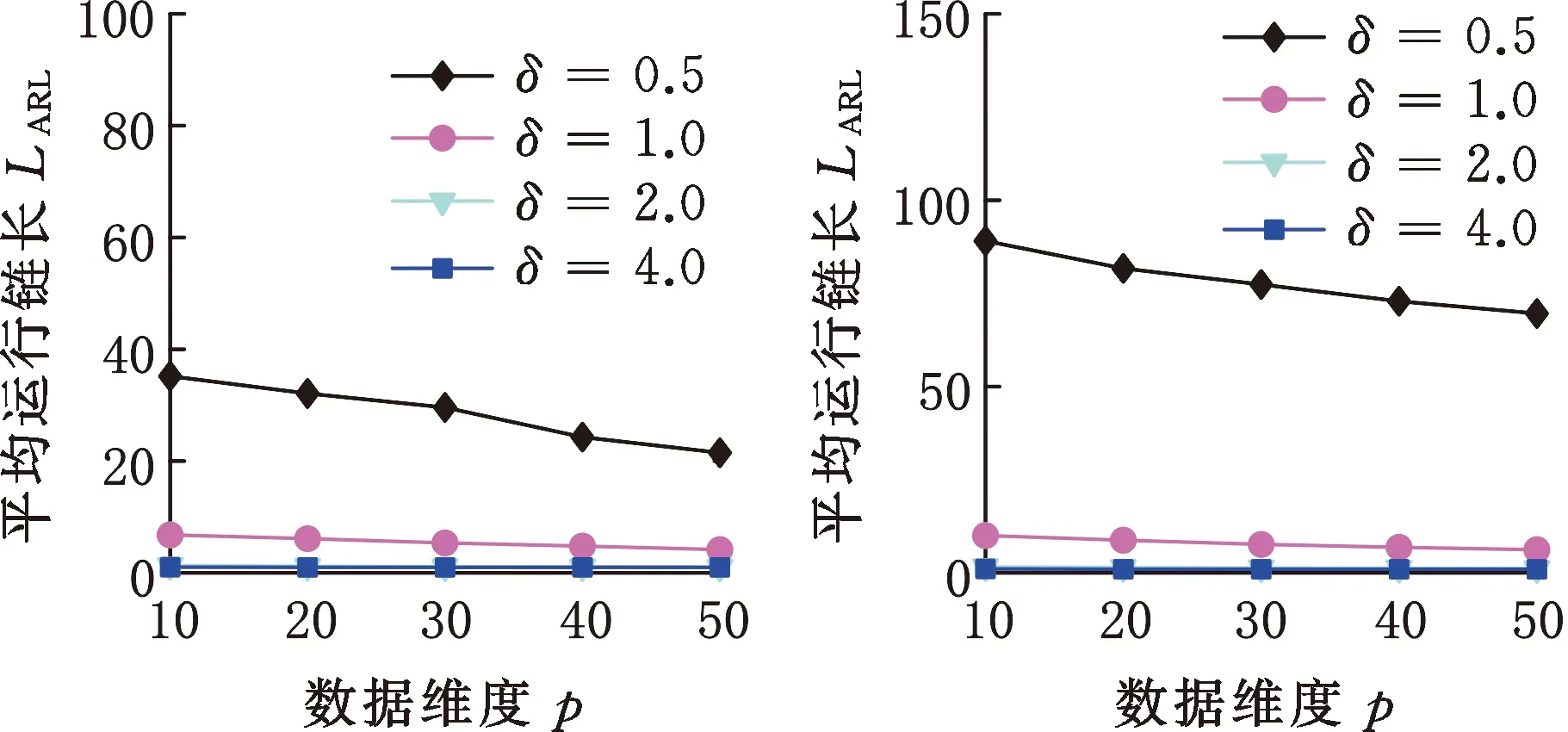
(a)Norm10 (b)t10，m5

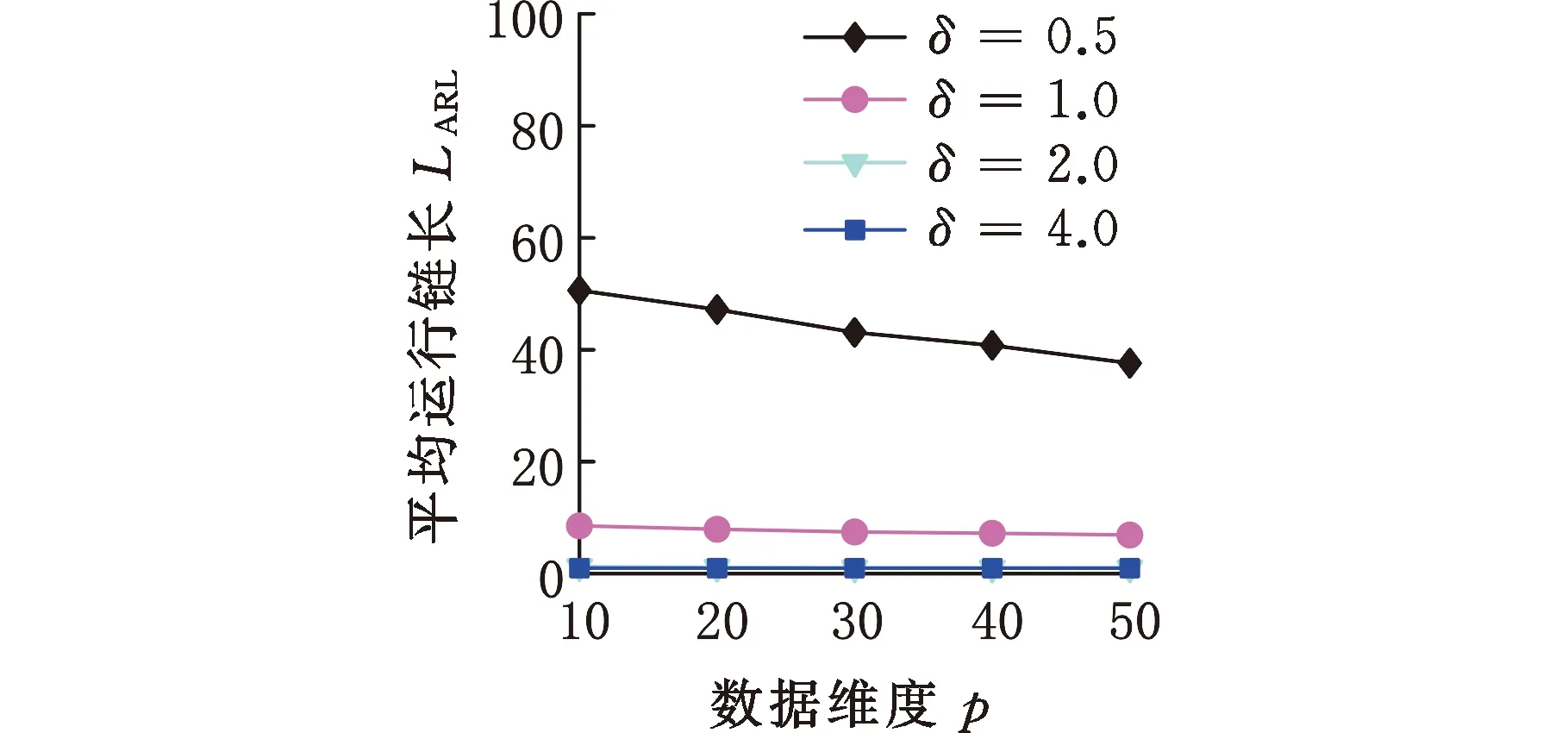
(c)Gam10,3图6 HREWMA控制图在不同维度下的OC ARL比较Fig.6 Comparison of OC ARL of HREWMA controlchart in different dimensions

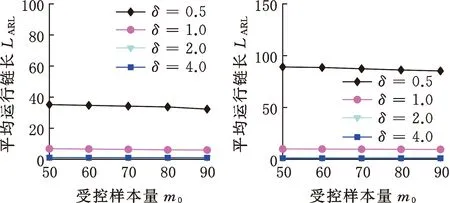
(a)Norm10 (b)t10,5

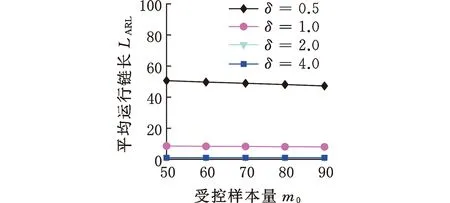
(c)Gam10,3图7 HREWMA控制图在不同受控样本量下的OC ARL比较Fig.7 Comparison of OC ARL of HREWMA controlchart under different controlled sample sizes

(4)漂移量的影响。由图8可知，随着漂移量的增大，3种分布的OC ARL均逐渐减小，尤其是HREWMA控制图在大漂移时具有很好的监控效果。

2.3 仿真结果讨论

结合表2、表3以及图8中HREWMA与其他控制图的比较，详述仿真的6个因素对HREWMA控制图监控效果的影响。

(1)平滑系数。对比发现，DFEWMA、SREWMA、SSEWMA控制图在平滑系数λ=0.05时对小漂移控制效果不佳，HREWMA控制图在λ=0.05时对小漂移有较好的控制效果。因此当平滑系数较小时HREWMA控制图同样具有良好的监控效果。

(2)样本量。当受控样本在50和90之间变化时，监控效果较为稳定，因此推断样本量增至50以上，监控效果较好且基本不受样本量的影响。

(3)滑动窗口。随着滑动窗口的增大，3种分布的监控效果均有更优的表现。其中多元t分布下，大的滑动窗口监控效果更好。

(4)数据维度。数据维度越大，HREWMA控制图的监控效果越，因此推断HREWMA适用于高维数据的检测。

(5)漂移量。与其他多元非参数控制图对比发现，HREWMA控制图在小漂移与大漂移的情况下均有较好的监控效果，其中对大漂移的监控效果极佳，在参与对比的控制图中达到最优水平。

(6)分布类型。HREWMA控制图在3种分布中均有较好的控制效果，对多元正态分布和多元Gamma分布有更优的监控效果。因此，HREWMA控制图具有普适性，能够有效监控分布未知的数据，并且推测对于多元正态分布和多元Gamma分布的数据具有较突出的表现。

3 实例分析

3.1 控制图在半导体生产中的应用

为了用高维数据集验证HREWMA控制图的性能，本文选取来自于MICHAEL[17]的数据集SECOM，记录了2008年7月至2008年10月通过半导体生产过程中的测量点的传感器收集得到的数据。共收集了1567个半导体产品的591维质量数据，得到的数据汇总为一个1567×591的矩阵。每个产品有分类标签，将该产品区分为合格样本和缺陷样本(±1)。在该数据集中合格品的样本量是1463个，不合格品的样本量为104个。挖掘庞大的高维数据，可以获得诸如产品质量特性分布、产品质量特性的变化趋势、质量特性之间的相关关系等信息。对数据进行正态性检验，根据图9中的QQ图和直方图，在不同维度下数据分布并非满足正态性假设，运用传统的基于正态性假设的控制图对SECOM数据进行检测，不能得到可靠的监控效果。

(a)Norm10(λ=0.05) (b)t10,5(λ=0.05) (c)Gam10,3(λ=0.05)

(d)Norm10(λ=0.1) (e)t10,5(λ=0.1) (f)Gam10,3(λ=0.1)图8 当λ=0.05/0.1、m0=50、维度p=10时控制图对比(OC ARL)Fig.8 Comparison of control charts when λ=0.05/0.1，m0=50 and dimension p=10(OC ARL)

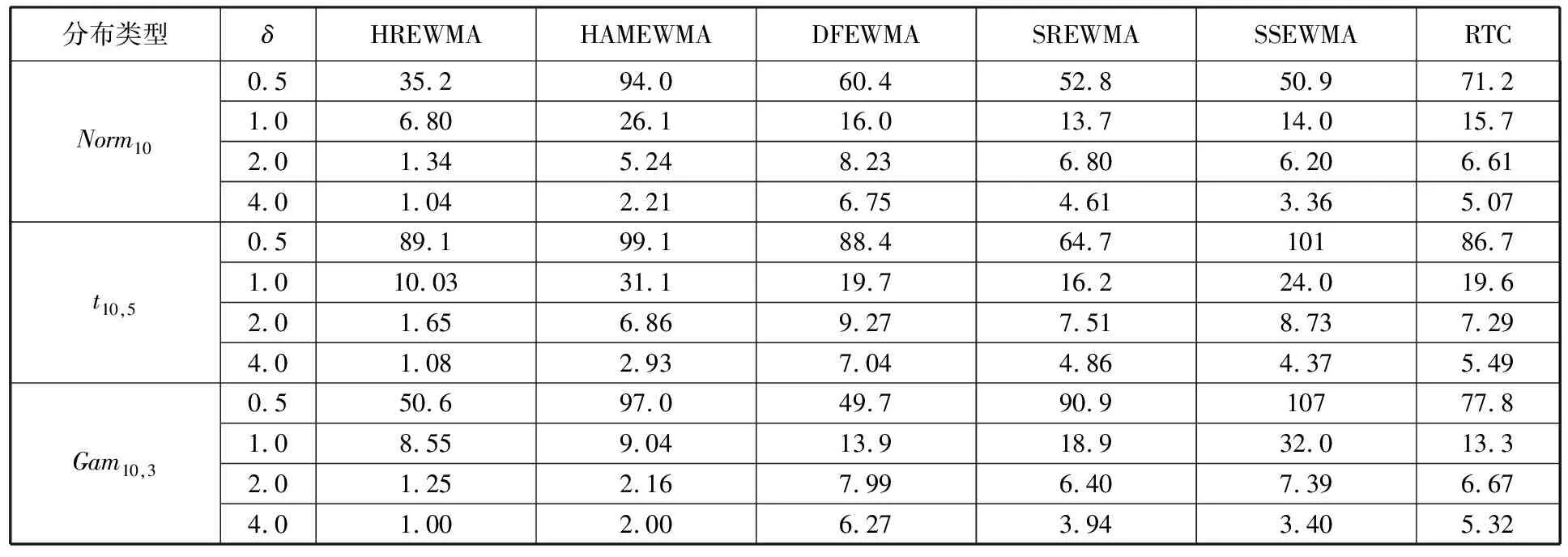
表2 当λ=0.05、m0=50、维度p=10时控制图OC ARL对比

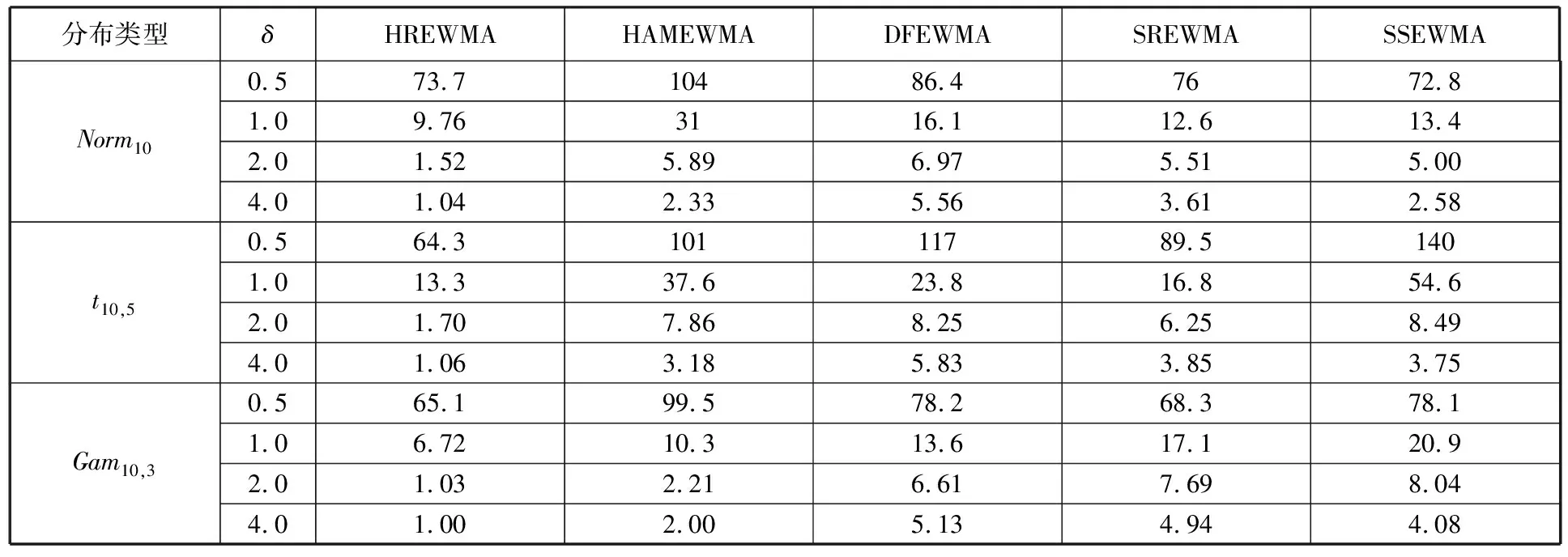
表3 当λ=0.1、m0=50、维度p=10时控制图OC ARL对比

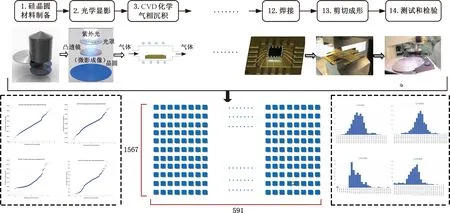
图9 半导体制造中高维数据的产生Fig.9 The generation of high-dimensional data in semiconductor manufacturing

运用HREWMA控制图对数据进行监控。在合格样本数据集中随机选取m0=50作为受控样本，控制图基本参数设置为LARL0=200，λ=0.05，D=10。首先根据控制图参数的设置利用受控数据集得到控制限，待监测样本由随机选取的15个合格样本数据和85个不合格样本数据组成，得到控制图见图10。在第17个数据时控制图判断数据异常并报警。

将HREWMA控制图在SECOM数据集上的运行结果与其他非参数控制图在SECOM数据集上的运行结果进行对比。LI等[12]提出的HAMEWMA控制图在含变点的SECOM数据集上(由15个受控样本和85个不合格样本数据组成)进行数据监控，在第25个数据时判定异常数据加入，控制图报警。CHEN等[9]提出的 DFEWMA控制图监控含变点的SECOM数据集(由63个受控样本和37个不合格样本数据组成)，在第71个数据点时控制图判定异常并且报警。与其他在SECOM数据集上进行监控的非参数控制图对比发现，本文提出的HREWMA控制图对异常数据的加入更敏感，控制图报警更快速，监控效果更佳。

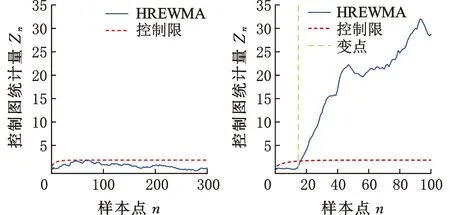
(a)受控的SECOM数据(b)含变点的SECOM数据

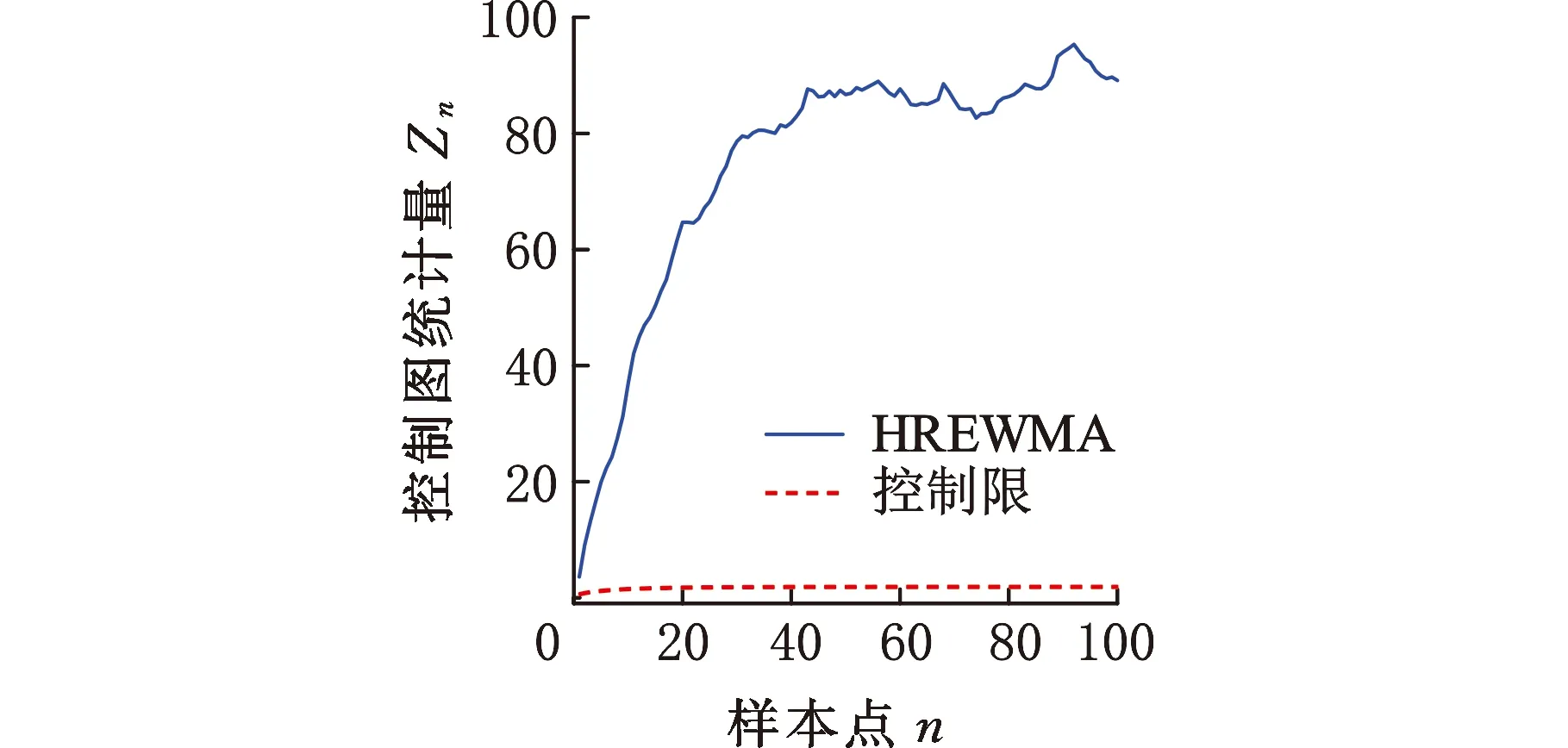
(c)失控的SECOM数据图10 HREWMA在受控、含变点、失控SECOM数据的监控效果Fig.10 Monitoring effect of HREWMA on SECOM dataunder control, including change points, and out of control

3.2 控制图在白葡萄酒生产中的应用

本文采用白葡萄酒生产中的高维数据来证明HAMEWMA控制图的实用性。白葡萄酒数据集(Wine Quality数据集)由CORTEZ等[18]提供，从UCI机器学习的资料库[17]中获取。数据集的时间区间为2004年3月至2007年2月，由生产白葡萄酒的自动化系统在多个采样点收集得到。白葡萄酒数据集由11个连续变量与1个分类变量组成，共包含4898个样本点。其中，11个连续变量表征白葡萄酒的性质，分别为：游离二氧化硫、总二氧化硫、密度、柠檬酸、挥发性酸度、固定酸度、硫酸盐、酒精度、残糖、氯化物、pH值。1个分变量表征白葡萄酒的质量，共包含从LV0(极差)到LV10(极好)的11个等级。

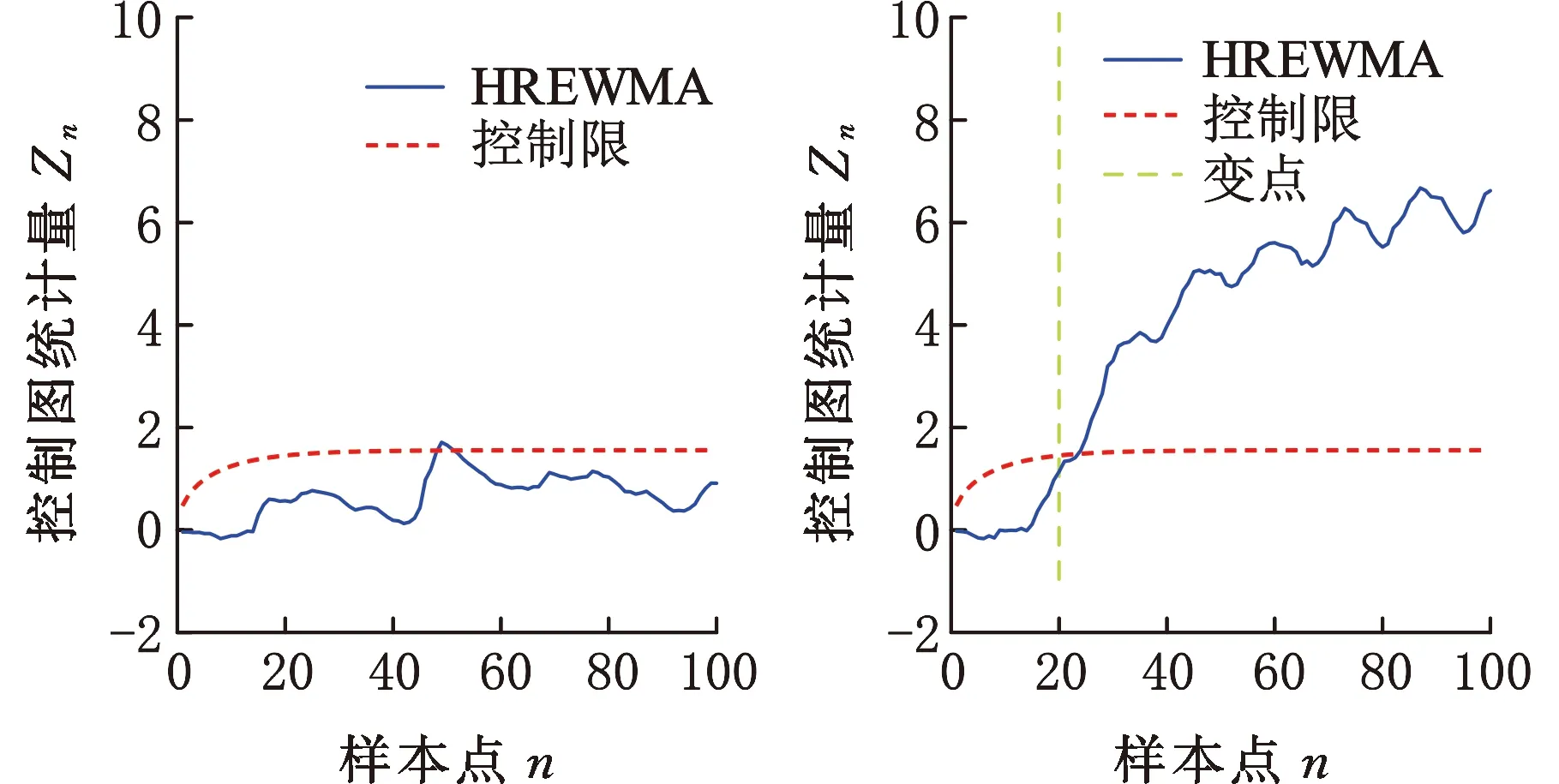
(a)受控的Wine Quality数据(b)含变点的Wine Quality数据

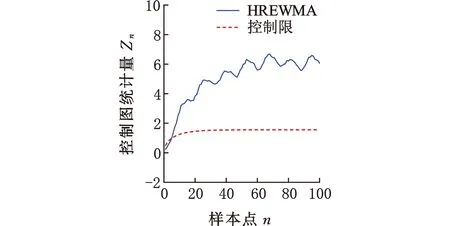
(c)失控的Wine Quality数据图11 HREWMA在受控、含变点、失控Wine Quality数据的监控效果Fig.11 Monitoring effect of HREWMA on WineQuality data under control, including change points,and out of control

依据HREWMA控制图对Wine Quality数据集进行监控，从LV7的数据中取m0=20个样本作为受控样本。设置控制图的基本参数LARL0=200，λ=0.05，D=10，根据仿真得到HREWMA控制图的控制限。按照顺序从LV7的数据集中随机抽取20个样本，从LV6的数据集中抽取80个样本，得到HREWMA控制图的监控效果如图11所示。在第25个数据点时控制图判断数据异常并且报警。ZOU等[10]在含有变点的Wine Quality数据集(由30个从LV7中选取的受控数据和70个从LV6中选取的不合格数据组成)上进行监控，在第55个数据点时控制图报警。与ZOU等[10]提出的SREWMA控制图相比，HREWMA控制图具有更好的监控效果，实用性更强。

4 结语

针对一些工业生产中存在的高维度、未知分布、受控样本小的数据特性，本文基于双样本高维秩检验设计了多元非参数HREWMA控制图,通过仿真分析和实例检验，证明HREWMA控制图具有更好的监控效果；并且通过与其他控制图的对比，证明HREWMA控制图对高维、小样本数据具有更好的表现；此外，HREWMA控制图在非正态数据中依然有良好的监控效果。与传统的多元非参数控制图比较发现，HREWMA控制图具有较好的监控效果，可以运用到实际生产控制中。