连续时间两级完全轮询接入MAC协议分析

杨志军，毛 磊，丁洪伟，寇倩兰

1.云南大学 信息学院，昆明650500

2.云南省教育厅 教学仪器装备中心，昆明650223

物联网是第三次信息产业革命的产物，其一经提出就获得了空前发展。它借助各种类传感器设备，对各类信息进行采集，并将处理后的信息通过互联网传递给用户，以此来实现人与人、人与物、物与物之间的任意通信。在这个过程中，物联网感知层内涉及多种不同优先级的业务，对不同业务进行区分非常有必要，这就需要用到媒介访问控制协议（medium access control，MAC）。MAC 协议规定了节点传输数据时占用无线信道的方式，它通过通信协议和通信机制，降低传输时延，提高网络的吞吐量和服务质量[1-2]。因此MAC协议性能的好坏决定了物联网的数据传输能力。通信网络中MAC协议数据传输的可靠性和实时性也一直是研究的热点[3-5]。文献[6]基于时分多址（time division multiple access，TDMA）的MAC 协议，提出一种BEST-MAC 协议用于无线传感器网络，该协议平均数据包延迟较小，相同时间内能够传输更多的数据。文献[7]提出一种新颖的基于动态公共控制信道的协议（DCCC-MAC），用于认知无线电网络，与传统的基于专用控制信道的MAC 协议不同，该协议消除了用于控制信息交换的专用信道的需求。文献[8]提出基于异步占空比的MAC 协议（ADPMAC），通过监视传入流量的变化来切换接收器节点的轮询间隔分布，研究发现当ADP-MAC的流量到达和轮询间隔分布一致时，就延迟和能量而言，性能都是最佳的。通过对比可知，上述研究虽然在一定程度上降低了网络时延，提高了MAC协议的性能，但并未对网络中业务的优先级进行区分。

基于轮询接入的MAC协议是一种非争用的接入机制，它在数据传输之前为各个节点分配信道资源，在整个通信过程中，占用信道的节点独享分配到的各项资源，从而使网络节点实现数据的无冲突传输[9-11]。轮询系统根据查询时刻节点发送信息分组的个数，可以分为完全服务[12]、门限服务[13]和限定服务[14]三种，其中完全服务模式用户的平均等待时延最低，限定服务模式的公平性最好，门限服务模型介于二者之间。由于无冲突的传输方式、轮询接入控制方式在无线传感器网络和计算机网络中有着广泛应用，随着研究的发展，它的服务方式也不断扩展[15-17]。文献[18]在离散时间基础上，研究了对称和非对称相结合的两级混合轮询控制策略，普通站点采用非对称门限服务模式，优先级站点采用完全服务模式，该系统能对网络中不同优先级的业务进行区分，但由于优先级用户和普通用户的服务模式不同，一定程度上降低了系统的公平性。同时该系统普通站点采用门限服务，用户的平均等待时延还有待提高。文献[19]中对站点状态进行区分，根据站点中是否有发送请求将站点分为忙闲状态，每次轮询时，服务器仅对忙站点进行服务，降低了网络能耗。文献[20]对门限服务模式进行了改进，将服务时间和轮询调度时间同步处理，提高了轮询接入控制MAC 协议的服务效率。两种MAC 协议分别从能耗和服务效率的角度，对轮询系统进行了研究，由于两种系统采用的都是单一服务模式，仍然没有解决区分优先级业务的问题。

上述对于轮询接入控制方式的分析，大多是采用时间离散型分析方法，系统的二阶特性求解相对复杂，而时间连续型分析方法能对系统的关键参数进行拉普拉斯变换，简化求解过程。本文在此基础上，提出两级完全轮询接入控制MAC协议，对用户划分不同的优先级，综合考虑物联网对实时性的需求，采用完全服务模式来保障网络的时延和服务的公平性。然后在时间连续型分析方法的基础上，构建数学模型，使用概率母函数的方法对该协议的一阶、二阶特性进行了解析，最后在MATLAB上进行仿真实验，对理论分析进行验证，并对该协议的性能进行分析。

1 系统模型

连续时间两级完全轮询接入控制模型由N+1 个节点和一个汇聚节点（服务器）共两级组成，第一级是N个普通站点，站点序号用{1,2,…,i,…,N}来表示，第二级是一个优先级站点，用下标h来表示，系统模型如图1 所示。物联网感知层的节点主要分为采集节点和汇聚节点，采集节点对环境中的数据进行采集；汇集节点按照规定的MAC协议接收各个采集节点的数据。在汇集节点接收数据的过程中，门限服务和限定服务模式都会产生中断，而完全服务只有在服务完一个站点，站点为空之后才会转去服务下一个站点，不会产生中断，三种模式中，它的平均等待时延最低。因此采用完全服务模式为优先级节点和普通节点提供数据传输服务。

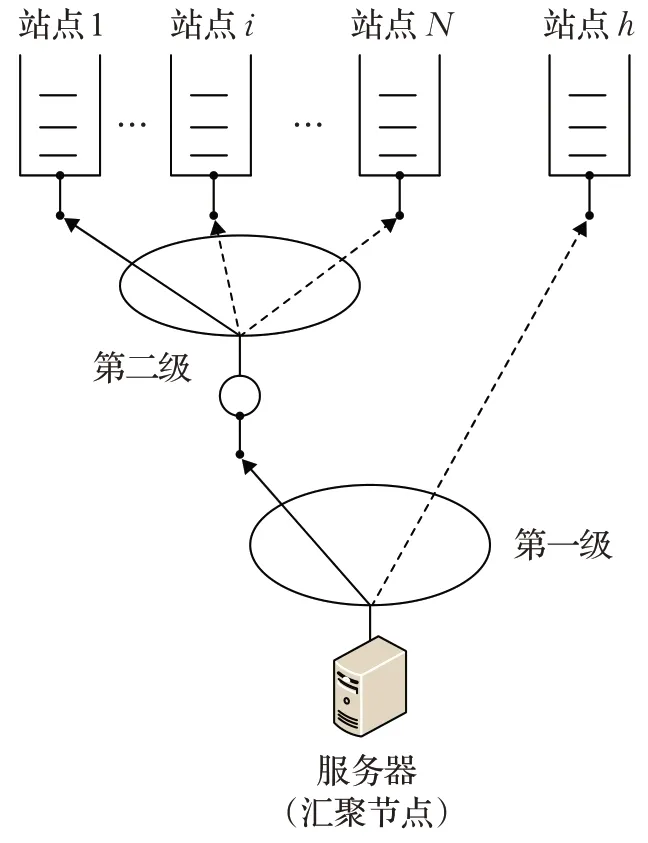
图1 系统模型Fig.1 System model

在连续时间的基础上，以时隙为单位划分时间轴。在任意一个时隙内，都有数据到达优先站点和普通站点等待传输。这里的连续时间指的是信息分组的到达是以某一时间点为准的，使用连续型分析方法，主要是为了对系统的关键参数做拉普拉斯变换。服务开始后，服务器首先对优先级站点提供服务，服务完成后转去查询普通站点，然后再查询优先级站点，以此类推。优先级站点向普通站点切换的时候，采用同步处理的方式节省转换时间，提高系统的服务效率，即服务器在为优先级站点提供完全服务的同时顺带查询i号普通节点。

2 数学模型

轮询接入MAC协议的性能，通常使用系统的一阶、二阶特性来描述。一阶特性指的是用户的平均排队队长、系统吞吐量和平均循环周期；二阶特性指用户的平均等待时延。因此定义随机变量，构建数学模型来分析该系统的性能。

2.1 系统工作条件

使用轮询控制机制进行数据传输时，各个节点之间的数据传输不会发生碰撞和冲突，但并不排除信道干扰等因素导致的数据传输失败现象。因此假设各节点之间的数据通信正常，汇聚节点的存储区不会发生数据溢出。

根据轮询系统的工作机制，通信过程中数据的到达过程和传输特性，定义以下工作条件：

（1）数据信息在任一个时隙内到达每一个站点的过程服从相互独立的泊松分布，普通站点的达到率为λi，优先级站点的到达率为λh。

（2）服务器每传输普通站点中的一个数据所需要的时间是独立、相同分布的概率分布，其随机变量的拉普拉斯变换（Laplace transform，LST）为，均值为，二阶原点矩为；优先级站点的分布为，均值和二阶原点矩分别为。

（3）服务器从i号普通站点向优先站点转移的时间服从独立、相同分布的概率分布，其随机变量的LST 为，均值为，二阶原点矩为。

（4）服务器按照数据到达的先后顺序为站点中的数据提供服务。

2.2 随机变量

为了对系统的性能参数进行分析，定义以下随机变量，如表1。

表1 随机变量定义Table 1 Definition of random variables

在对系统进行建模时，考虑三个时刻，tn、tn*、tn+1(tn+1＞tn*＞tn)。假设tn时刻，服务器开始对i号站点中的数据进行传输，此时系统的随机变量为{ξ1(n),ξ2(n),…,ξi(n),…,ξN(n),ξh(n)}；tn*时刻，服务器完成对i号站点的服务，转向优先级站点提供完全服务，此时系统的状态变量可表示为{ξ1(n*),ξ2(n*),…,ξi(n*),…,ξN(n*),ξh(n*)}；tn+1时刻服务器又转换到i+1 号普通站点，系统的状态为{ξ1(n+1),ξ2(n+1),…,ξi(n+1),…,ξN(n+1),ξh(n+1)}。通过分析可知，tn时刻系统的状态只与tn*时刻有关，tn+1时刻系统的状态只与tn*时刻有关，该系统的N+1 个状态构成马尔可夫链，由于系统内站点数量是确定的，服务器按照轮询顺序依次访问各个站点，所以该马尔可夫过程是有限和各态历经的。

2.3 概率母函数

根据定义的随机变量和服务器的轮询顺序，可以得到下列关系式：

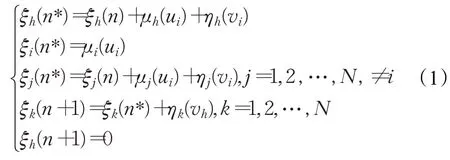
为了准确构建系统的数学模型，引入概率母函数的分析方法，上面描述的嵌入式马尔可夫链在的条件下保持稳定，其中ρi=λiβi表示系统负载。

稳态时，系统状态变量的概率分布函数为：

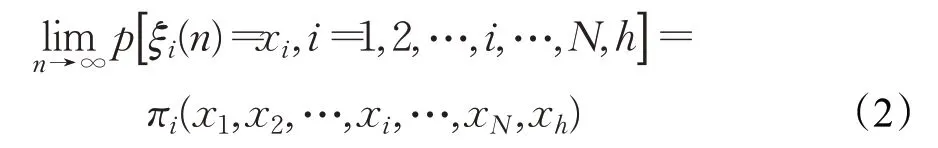
通过对概率母函数的定义分析可以得到，πi(x1,x2,…,xi,xN,xh)的母函数为：

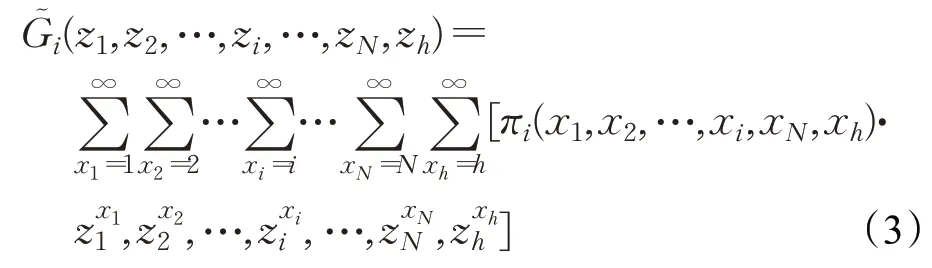
tn*时刻服务器为优先站点提供服务，此时，系统变量的概率母函数为：

tn+1时刻转换到i+1 号普通站点，系统变量的概率母函数为：

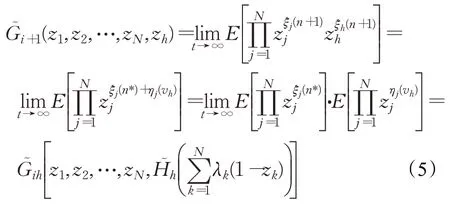
3 系统特性解析

3.1 平均排队队长

定义1每个站点内等待发送的信息分组数为平均排队队长。tn时刻，i号站点开始传输数据时，j号站点的平均排队队长为，则

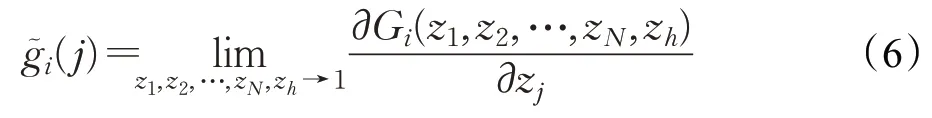
3.2 平均循环周期

定义2 系统的平均循环周期为服务器按照规定的轮询顺序对所有站点完成一次访问所经历的时间，也就是服务器对同一个普通站点连续两次访问所经历的时间间隔，计算如下：

3.3 系统吞吐量

定义3 系统吞吐量为单位时间内完全服务两级轮询系统所能传输的信息量，用T表示，计算方式为：

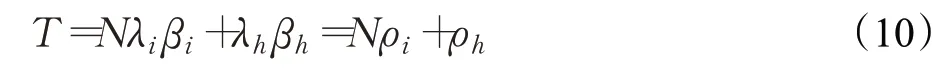
3.4 一阶特性

定义4表示i号站点接受服务期间，k号站点中等待的数据包的平均排队队长，则：

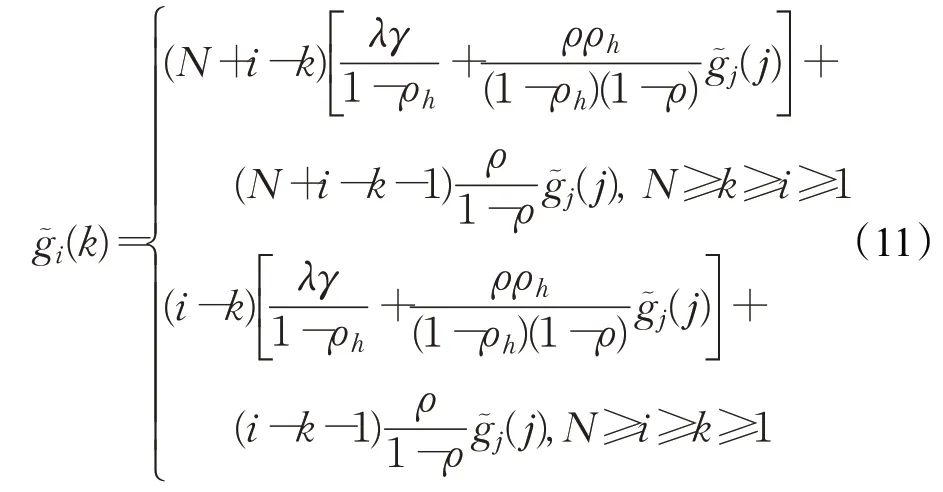
3.5 二阶特性

定义5 普通站点随机变量(xj,xk)的联合矩为；优先级站点随机变量(xj,xk)的联合矩为，则由概率母函数可得：

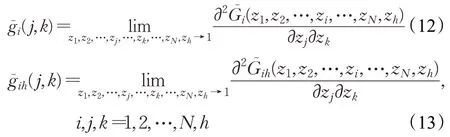
将式（4）、（5）代入式（12）、（13）可得：

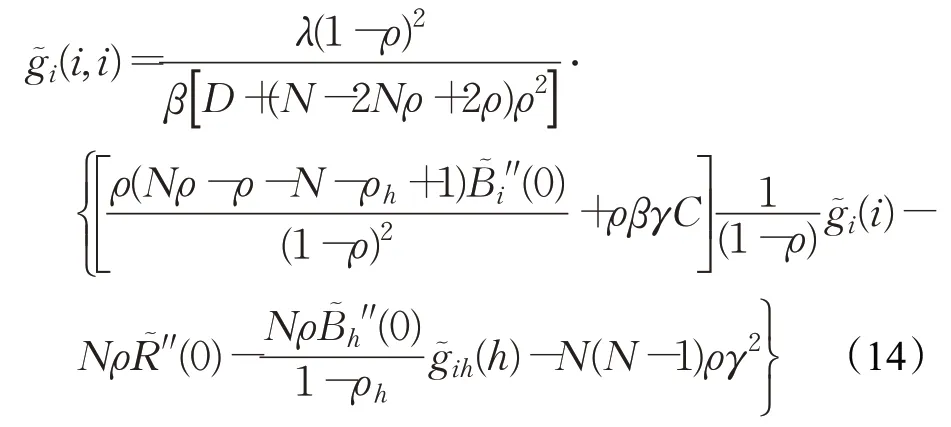
其中，C=(N-1)(2ρρh-N)+2ρh(ρh-1-N)，D=[(N-1)ρ-(1-ρh)][(1-ρh)(1-ρ)2+ρ2]

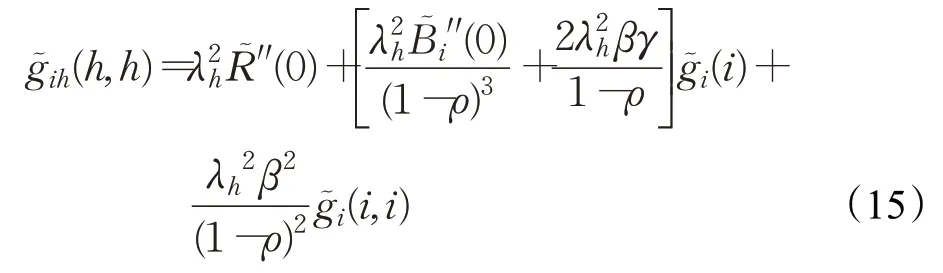
3.6 平均等待时延

定义6 系统的平均等待时延为信息分组数从进入站点直到其被发送出去的时间间隔。用E[Wi]和E[Wh]分别表示普通站点和优先级站点的平均等待时延，则根据文献[12]，将式（7）、（8）、（14）、（15）代入可得。

普通站点的平均等待时延为：

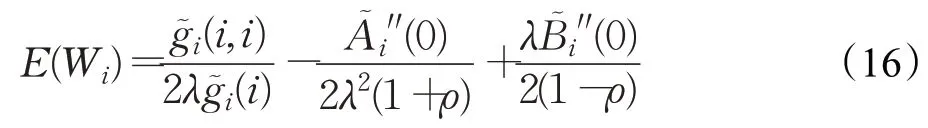
优先级站点的平均等待时延为：

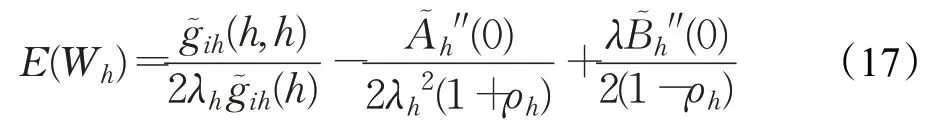
4 仿真实验及性能分析

4.1 仿真实验

根据3.1节定义的条件，在MATLAB2018a平台上进行仿真实验，验证理论分析的可靠性。系统在+λhβh＜1 的条件下保持稳定，根据式（7）～（10）、（16）、（17）计算出理论值，然后与实验值比较。

在该系统中，其初始化条件为开始时刻，各个站点内没有信息分组需要发送。站点提出发送请求后，服务器首先对优先级站点中的数据进行传输，直到站点内所有数据被传输完毕。然后转去访问i号普通站点，对i号站点内的数据进行传输，发送完所有的数据后，又再次转去查询优先级站点h，以此类推，服务完优先级站点后，又转去查询i+1 号普通站点，即轮询顺序为：h→1→h→2…h→N→h→1。系统控制算法流程如下所示：

实验中相关参数设置参照IEEE802.11n标准。基于Matlab 伪随机数，生成到达率为λ的泊松分布序列，用于模拟系统各队列单位时间内到达的信息分组数，到达率越大，单位时间内到达系统的信息分组数越多。在信道传输速率和服务器处理能力一定时，排队等待的数据也就越多。采用服务时间变量记录系统中数据服务消耗的时间累计，数据序列每减少一个单位，服务时间变量累计一个服务时间，用β表示，β越小，表明系统数据处理能力越强，吞吐量越大。查询转换时间γ是衡量轮询效率的重要指标，γ越大，系统轮询一周的所花时间越长，效率越低。在无线传感器网络中，节点数表示网络规模，节点数越多网络规模越大。信道速率表示单位时间内信道上所能传输的数据量。实验中按间时隙划分时间轴，1 时隙等于10 μs，每个信息分组的长度设定为1 000 Byte。具体参数设置如表2 所示，仿真结果为相同参数下10万次蒙特卡洛实验统计。

表2 仿真实验参数设置Table 2 Parameter setting of simulation experiment

4.2 性能分析

实验中，通过改变数据的到达率和网络的节点个数，分析系统平均排队队长、平均等待时延和平均循环周期的变化规律，如图2～5 所示，首先从各图都可以看出理论值与实验值一致，说明理论分析是完全正确的，接下来对系统的性能做进一步分析。

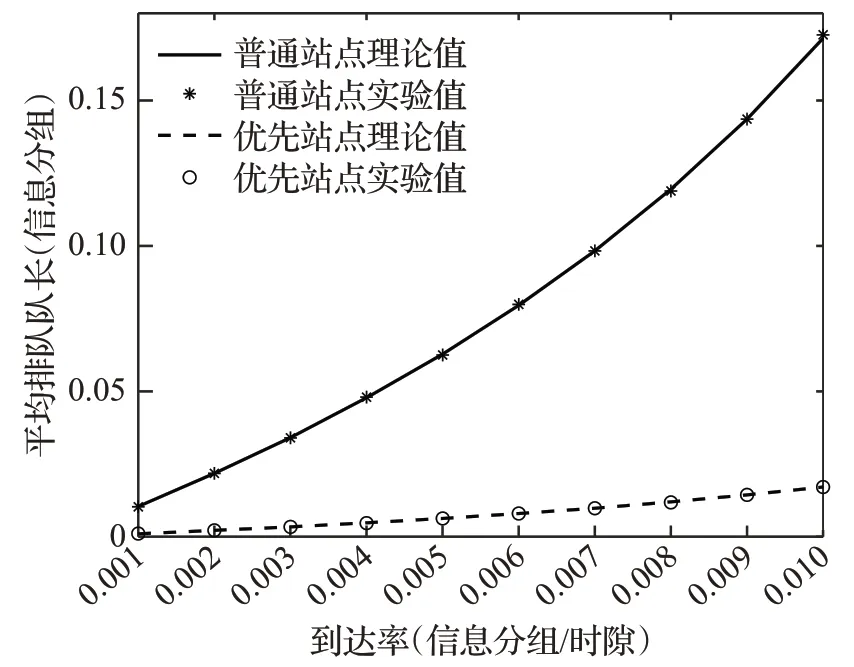
图2 平均排队队长与到达率的关系(λ=λh,β=βh=4,γ=1,N=10)Fig.2 Relationship between average queue length and arrival rate

图2 和图3 是系统平均排队队长、平均等待时延与到达率的关系。从图可以看出无论是普通站点还是优先级站点，当服务时间、转移时间和站点数量固定不变时，平均排队队长和平均等待时延与到达率是正相关的。普通站点平均排队队长和平均时延的变化是同步的，平均排队队长越长，相应的平均等待时延也越大。对比普通站点和优先站点的平均排队队长和平均等待时延，可以看出，优先站点的平均排队队长和平均等待时延远远小于普通站点。随着到达率的增大，这种区分仍然很明显，说明该系统能对不同优先级的业务进行区分，并且区分的效果很好。

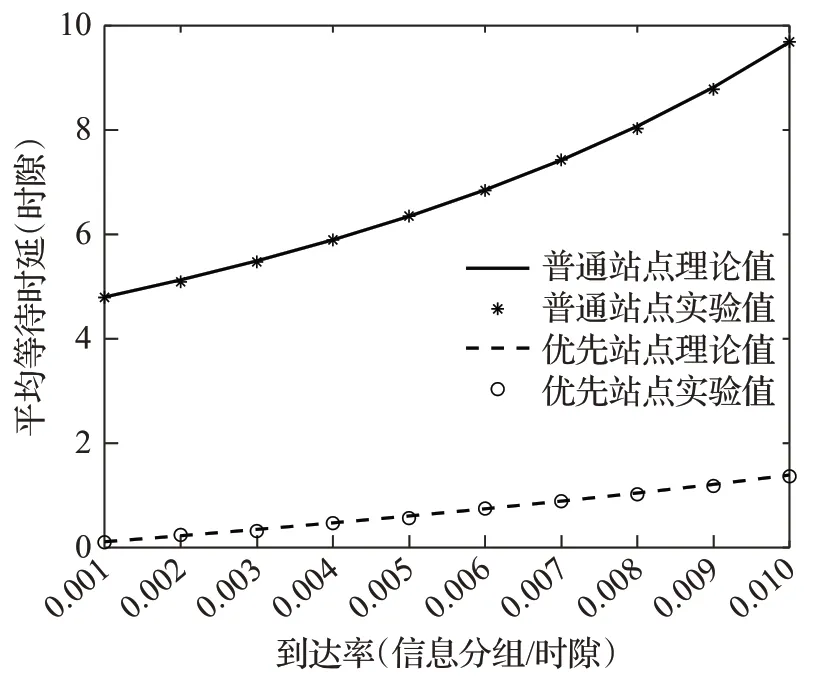
图3 平均等待时延与到达率的关系(λ=λh,β=βh=4,γ=1,N=10)Fig.3 Relationship between average delay and arrival rate

表3是不同参数下，普通站点和优先级站点平均排队队长和平均时延理论值与实验值的对比，实验中，优先站点和普通站点的参数不同。首先可以看出，理论值与实验值基本拟合，误差保持在较小范围内。进一步分析，在普通站点和优先站点参数不同的情况下，无论是普通站点的到达率和服务时间大于优先站点，还是优先站点的到达率和服务时间大于普通站点，优先站点的平均排队队长和平均时延总是小于普通站点，说明两级完全服务区分优先级业务的能力较强。

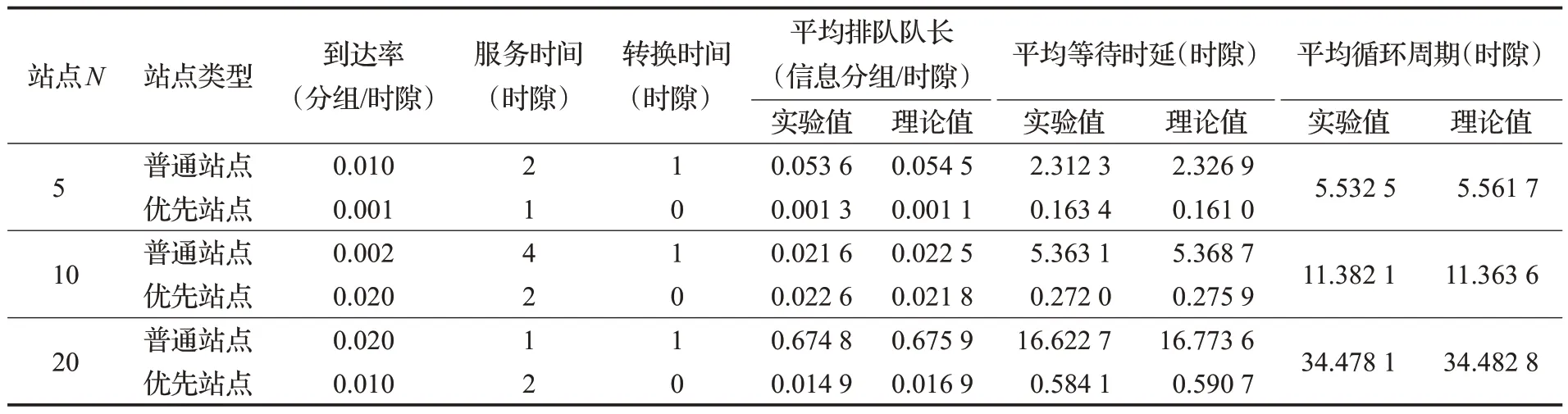
表3 普通站点和优先站点实验值与理论值对比Table 3 Comparison of experimental values and theoretical values of ordinary stations and priority station

图4是不同数量站点下，系统平均循环周期随到达率的变化关系。可以看出，不同数量站点下，系统的平均循环周期随着到达率的增加而增大。当到达率和站点数量较小时，系统很快就能完成对所有站点的轮询，说明系统的响应速度较快。从三条曲线的垂直分布来看，站点数量也是影响系统平均循环周期的重要因素，在到达率一定时，站点数量越多，周期越长，系统的响应速度越慢。

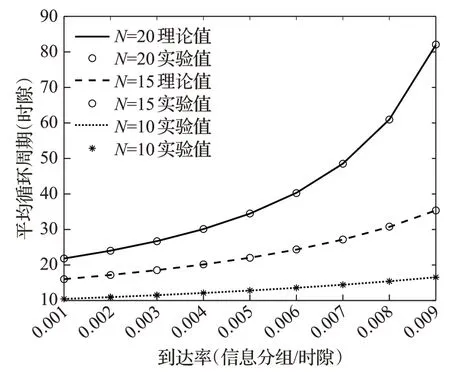
图4 不同站点平均循环周期随到达率的变化(λ=λh,β=βh=4,γ=1)Fig.4 Change of average cycle with arrival rate at different sites

图5 是系统吞吐量与到达率的关系，实验中，可以看出吞吐量随着到达率线性增加，说明当普通站点和优先站点的到达率相同时，吞吐量与到达率是线性关系，这与理论分析是吻合的。

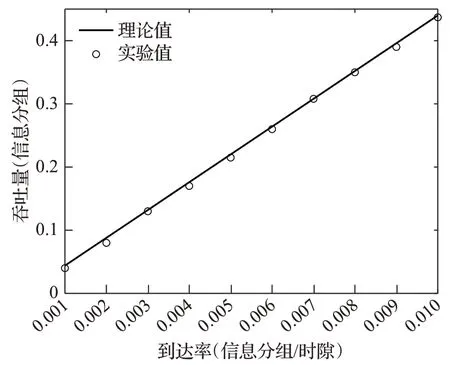
图5 吞吐量与到达率的关系(λ=λh,β=βh=4,γ=1,N=10)Fig.5 Relationship between throughput and arrival rate

图6和图7是两级完全服务与单级完全服务平均排队队长、平均等待时延的对比分析。为了保证实验的准确性，两种协议的网络规模应该一致。因此实验中，单级完全服务设置11个站点，11个站点的优先级一致，两级完全服务设置10个普通站点和一个优先级站点。首先对比普通站点的平均排队队长和平均时延，两级完全服务普通站点的队长和时延都小于单级完全服务，说明优先级站点使得整个系统的性能发生了改变，设置两级服务对不同优先级的业务进行区分，在一定程度上优化了普通站点的性能。然后对比两级完全服务优先站点的平均队长和平均等待时延，可以看出，优先站点的队长和时延远远小于普通站点和单级完全服务，说明连续时间两级完全服务区分业务优先级的效果显著，达到了提出该系统的初衷。从控制机理的角度来分析，两级完全服务将原有单级完全服务中的N+1 个同优先级站点划分为1个优先级站点和N个普通站点，在一次轮询过程中，服务器对优先级站点提供N次完全服务，而每个普通站点仅提供一次完全服务，所以优先级站点的平均排队队长和平均等待时延远远小于普通站点。一次轮询过程中，多次服务优先站点，保障了优先业务能够及时得到服务，满足了系统内优先业务或核心业务对实时性的要求。

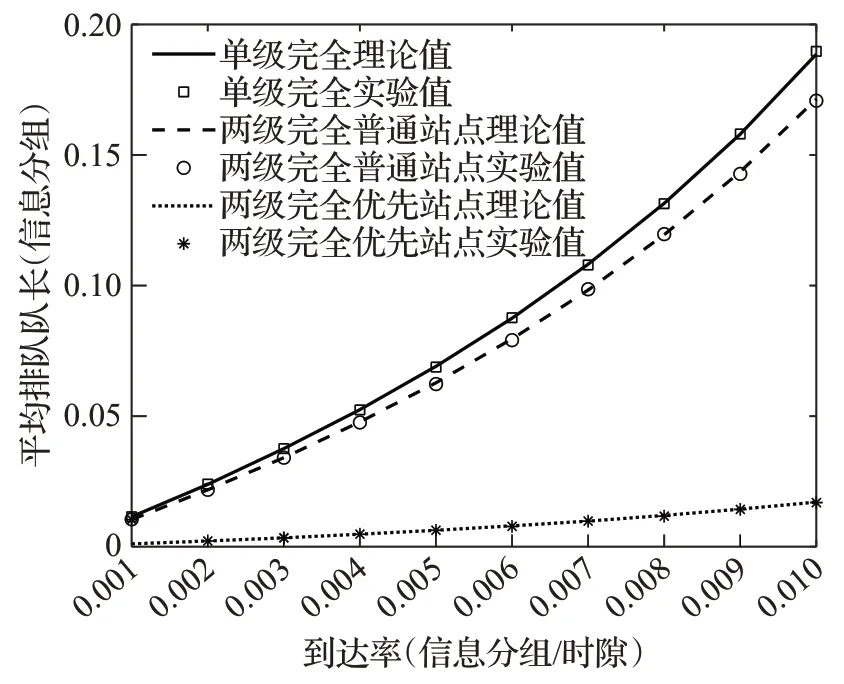
图6 两级与单级完全服务平均排队队长对比(N=10,β=4,γ=1)Fig.6 Comparison of average queue length between two-level and single-level exhaustive service

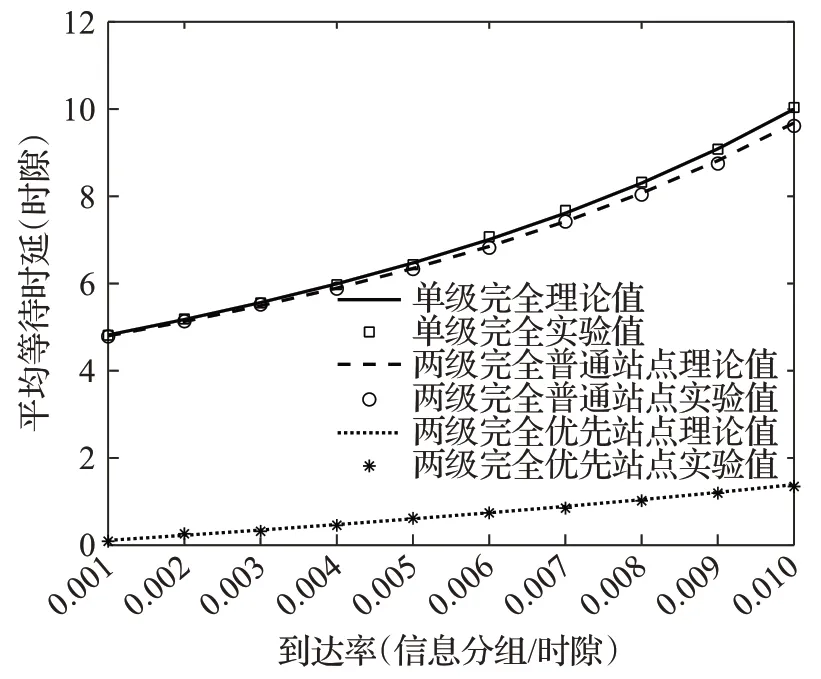
图7 两级与单级完全服务平均等待时延对比(N=10,β=4,γ=1)Fig.7 Comparison of average delay between two-level and single-level exhaustive service

4.3 对比分析

图8是本文协议与文献[18]提出的混合轮询控制策略和文献[20]提出的并行调度门限服务策略的对比分析。在网络参数相同的情况下，与文献[18]对比，本文所提协议普通站点和优先级站点的平均等待时延更小，说明本文所提协议性能更优；与文献[20]对比，本文所提协议在区分优先级业务的同时，降低了普通用户的平均等待时延，提高了系统的服务质量。

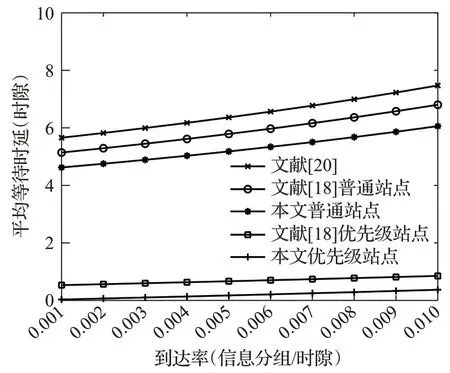
图8 三种协议平均等待时延的对比分析(N=11,β=βh=2,γ=1)Fig.8 Comparative analysis of average delay of three protocols

表4是文献[17]提出的门限、完全两级服务与本文提出的连续时间两级完全服务模型的平均队长和时延对比分析。从表中可以看出，在到达率一样的情况下，两种模型的平均排队队长是一样的，说明改变服务方式不会影响系统中的顾客数。从平均等待时延来看，连续时间两级完全服务的时延要小于门限、完全两级服务。表明本文提出的两级完全模型性能更优，在区分优先级的同时，又能获得较小的平均等待时延和更高的服务质量。相同业务量的情况下，本文模型能更好地满足核心业务或优先业务对于实时性的要求，同时，由于普通站点和优先站点都使用相同的服务方式，进一步确保了用户的公平性。

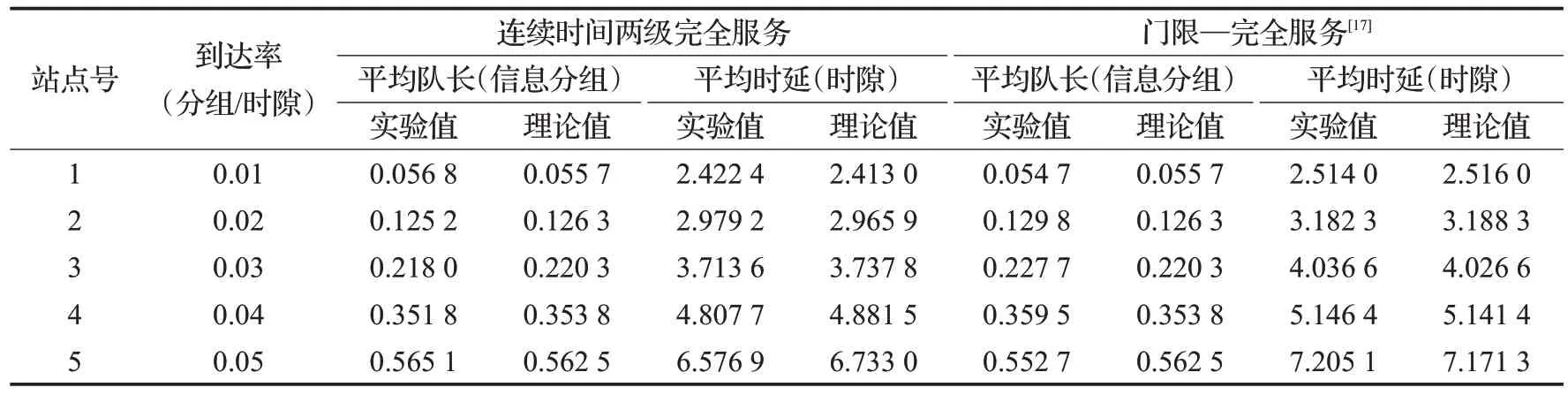
表4 两种模型普通站点平均排队队长和平均时延对比Table 4 Comparison of average queue length and average delay between two models

5 结束语

本文使用连续时间的分析方法，提出一种区分优先级业务的两级轮询接入协议，普通站点和优先站点都使用完全服务。然后运用数学分析方法对该协议进行建模，精确解析出了该系统的一阶特性和二阶特性。最后运用仿真实验对理论分析进行验证并分析了系统的性能。通过实验分析，可以看出本文提出的两级完全服务模型，在对不同优先级业务进行区分的同时，保证了普通站点的服务质量。该系统在一次轮询中，多次访问优先站点保证了优先业务可以优先得到服务，而普通站点使用时延较小的完全服务，不仅降低了普通用户的等待时间，还保证了公平性。与单级完全服务轮询系统相比，该系统不仅适应了物联网中优先级业务的需求，还优化了普通业务；与其他两级轮询模型相比，该系统普通站点的平均时延较小，实时性更高。在今后的研究工作中，可以划分更多的优先级来进一步提高该协议的服务质量。