相互依赖网络的多参数混合幂次迭代瓦解策略

付 豪，刘三阳，白艺光

西安电子科技大学 数学与统计学院，西安710126

进入21 世纪，人类之间的社交关系由于科技的进步变得更为紧密。基于关系的社交网络正在从传统网络结构向大尺度、高密度的形态转变。更为复杂的网络结构往往会为人类带来巨大挑战，如2019 年12 月爆发的Covid-19新冠肺炎，病毒伴随着更为便捷的交通网络与更为密切的社交接触，向全球快速蔓延，对人类社会的正常运转带来了巨大挑战。因此对各种基于复杂网络的社会行为进行更深入的研究是有重要现实意义的。事实上单一的网络结构不能准确、完整地描述现实生活中复杂问题的相互联系。绝大多数严重灾害都是由小事件引发的，这些小事件可能会在更为复杂的相互依赖网络中引发一连串的故障，甚至导致网络完全崩溃[1-2]。

在复杂网络系统中，相互依赖网络由于其不同子网络的相耦合性，导致相互依赖网络比单层的网络更加脆弱。因此，其对于某个局部的攻击将更加敏感，容易出现大规模的网络瘫痪灾难，如2003 年北美大停电[3]、2004 年意大利大停电等[4]。因此研究这些网络的鲁棒性对于防止网络系统崩溃至关重要。对相互依赖网络的研究是一个吸引人且活跃的领域。

网络瓦解是指通过移除某些节点，使连通网络分裂成不相连的簇甚至使整个网络结构崩溃，目的是找到使得网络完全崩溃的最小节点集[5]。网络最优瓦解策略已经引起了大量研究者的关注，并被应用在许多新兴领域，包括病毒控制[6]和交通网络分析[7]等。网络的最优瓦解问题是一个NP-Hard问题，无法在多项式时间内进行有效求解。在单个网络中，众多研究者基于节点中心性指标（如度、介数、k-Core、PageRank等）提出了大量的关于网络最优瓦解的方法（随机攻击（RA）、基于重叠度攻击（OD）、基于重叠介数中心性攻击（OB））[8-9]。尤其是节点排序问题被专门用来度量给定网络中节点的重要性[8，10]，实验表明，攻击重要性更高的节点，能够使得网络崩溃得更快。对应的，Iyer等人提出了各种基于中心性的瓦解方法，包括：基于邻域的局部中心性（度中心性、局部中心性[9，11]），基于位置的全局中心（紧密性中心性、介数中心性、k核中心性[12-13]）以及路径计算中心性（特征向量中心性、Katz中心性、PageRank、RA中心性[14-15]）等。

由于网络系统的多样性，每个网络中的关键节点可以从不同的角度被具体化。例如，影响力最大化问题中的关键节点是传播信息的影响源[16]；网络中断问题中的关键节点是保持网络完整性[17]的中间节点。其中，影响力最大化问题近年来备受关注，针对该问题提出了多种单节点排序方法[18]和多种随机识别方法[19]。同时，时序网络的节点排序方法也开始受到研究者们的关注[20]。因此，关键节点在不同的应用背景中可能有不同的含义，对于关键节点的定义目前并没有普遍的共识。Zareie 等人提出了一种基于熵的节点向内排序方法[21]。Wu 等人提出了一种基于两个互补物理过程的算法，用于度量节点的重要性[22]。

相互依赖网络不同于单一网络，因为其内在关系的种类更多，不同层之间的相互联系使得其结构也更加复杂。Schneider等人根据度中心性和介数中心性来识别节点，并选择最小数量的节点，以保证鲁棒性的平滑过渡[23]。Wang 等人提出了一种邻居节点优先连接耦合策略[24]。Song提出一种算法来识别重要节点[25]，其在每次迭代中选择一个尽可能降低系统结构强度的节点。Osat等人拓展模拟退火（SA）、高阶退火（HD）和高度自适应（HDA）等算法到多层网络[26]，以解决最优渗透问题。Zhao等人提出了一种逆向爆发渗透算法（IEP），是一种基于网络重构的渗透算法[27]，在IEP中，从所有未插入节点中随机选取m个候选节点以降低计算复杂度，并以节点的重叠度作为进一步的基准，然而，其结果并不是鲁棒的。

由于现有的中心性测度大多集中在特定的结构特征上，对节点的真实排序有一定限制。前文提到的各种中心性措施都趋向于高度值节点，然而，有研究人员发现，许多低度节点在复杂系统中也是有重要意义的[28]。因此，为了准确识别关键节点，需要优化中心性测度，尽可能全面地捕捉网络节点的结构信息。为了说明这一思想，图1给出了具有不同结构特征的重要节点的例子。

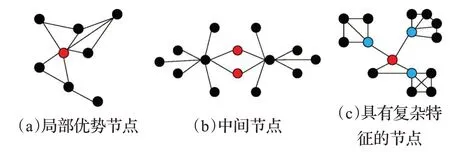
图1 具有不同结构的重要节点Fig.1 Significant nodes with different structures

图1（a）中红色的局部优势节点保持与大部分网络节点的连接，图1（b）中红色的中间节点保证了网络的完整性，对网络组件之间的交流有更多的控制，图1（c）中蓝色节点具有局部优势节点的特征，红色节点同时具有局部优势节点和中间节点的特征。可见，带有红色和蓝色节点在网络结构中起着至关重要的作用，准确的节点排序需要考虑所有的结构特征。

事实上，高影响力邻居节点对中心节点的影响大于低影响力的邻居节点，如果一个节点有很多高影响力的邻居节点，那么这个节点就具有更高影响力。本文的目标是解决关键节点识别问题，受两个经典物理过程（质量扩散MD和热传导HC）机制的启发，提出了一个复杂而有效的中心性迭代方法来全面捕获网络结构信息。首先，利用邻居节点对每个节点的影响提出一种改进幂次迭代排序算法。接着，从所有候选节点中选择会导致剩余集群最小的节点，以快速瓦解相互依赖网络。此外，在该算法中，定义了一种新的权重加权迭代机制，并探讨了所提加权迭代机制的合理性。为了评估所提出的算法的性能，分别将其应用于合成网络和真实网络。

本文主要贡献：（1）通过充分耦合MD 和HC 两个经典处理方法，可以深入挖掘出“影响力弱”的重要性节点，而这些节点往往在已有的算法中所忽视。（2）基于幂次迭代的排序提供了剩余集群的局部更新策略，极大提升了计算效率。

实验结果表明，本文方法在网络最优瓦解问题上优于其他先进的方法。

1 模型定义

1.1 相互依赖网络模型

双层相互依赖的网络模型A(VA,EA)-B(VB,EB)，由两个相互依赖的子网络A(VA,EA)和B(VB,EB)组成，两个子网络有着相同的节点数量N，通过相互耦合连接形成一个完整的相互依赖网络。其中，VA和EA分别是网络A的节点和连接边，VB和EB分别是网络B的节点和连接边。只有当节点属于其所在的子网络层的最大连接集群，该节点才会保持功能，否则该节点将失效。图2中一对一相互依赖网络结构，上子网中的每个节点都依赖于下子网中的一个且只有一个节点，反之亦然。

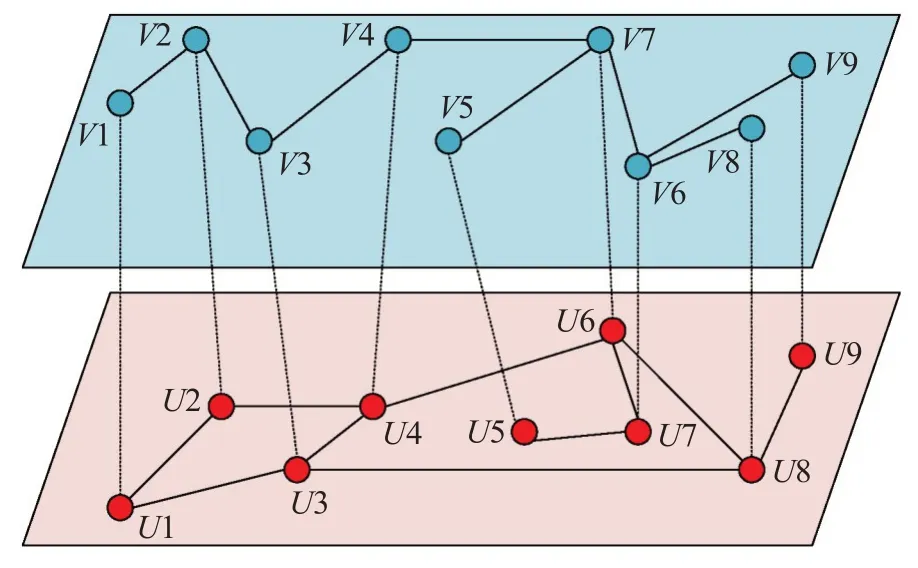
图2 相互依赖网络模型Fig.2 Interdependence network model

1.2 级联失效和GMCC

网络中一个或多个节点的故障可能导致多米诺骨牌效应，使得失效节点的邻居节点甚至是所有节点从整个相互依赖耦合网络里面断开，最后导致整个网络崩溃，这个过程称为级联失效过程。在相互依赖的网络中，通常的级联故障是由移除网络节点而引发的，初始移除一个节点往往等于移除它的从属节点。例如在图3中，移除子网A上的一部分节点后，B中所有连接到A中这些节点且未运行的节点都将失效，进而导致这些不再属于两个子网庞大集群的节点失效。直到A和B上没有节点被移除，这个动态过程才会结束。剩余网络中的有效节点形成一个簇，称为巨型相互连接集群（GMCC）。

图3 中实线表示内部链路，虚线表示外部链路，长方型为被攻击节点，正三角表示不属于巨型集群的节点，黑色圆用符号表示没有依赖节点的节点，蓝色圆表示功能节点。

图3 级联失效过程Fig.3 Cascading failure process

1.3 参数

考虑有N个节点的无向网络A(VA,EA)和B(VB,EB)，通过一对一的条件进行相互耦合，假定Ai只是依赖于Bi，则邻接矩阵分别为A=(aij)N×N和B=(bij)N×N。

网络A中节点i的度定义为：

在耦合网络中，节点Ai的重叠度[25]表示为：

网络A中节点i的介数中心性定义为：

在耦合网络中，节点Ai的重叠介数中心性[25]可以表示为：

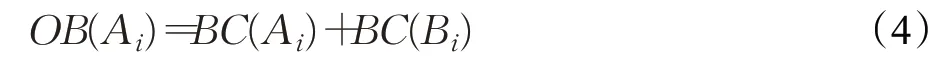
1.4 标准质量扩散（MD）和标准热传导（HC）

一个无向网络可以表示为G(V,E)，其中V为节点的集合，E为边的集合，ri为节点i的资源，Γi为其邻居的集合。标准的质量扩散（MD）过程首先通过为节点分配初始资源级别ri=ri(0)，在每次迭代中，每个节点的资源被均匀地重新分配给它的邻居。在这个再分配过程中，每个节点更新的资源等于它的邻居贡献的总和，数学上表示为：

其中，dj为节点j的属性指标，在本文的策略中使用网络的重叠度和重叠介数中心性，rj(t)为节点j在t时刻的资源占用级别。通过再分配过程的迭代，网络中所有节点的资源趋于稳定。当资源不再变化时，这个过程就会收敛并达到平衡。一个节点所保留的资源与迭代更新中其他节点释放的资源到达该节点的概率成正比。网络节点的重要性排序是通过对所有节点按照其最终资源的取值大小进行降序排列来生成的。

与MD 过程类似，热传导（HC）过程也以类似于无规则过程的方式重新分配资源。网络节点的初始温度不同，热从高温节点传递到低温邻居节点。不同之处在于，HC过程通过一个最近邻平均过程更新节点的状态，在这个过程中，它们的邻居的温度总和除以它们的度数，而MD过程通过将资源平均分配给最近的邻居来工作，HC过程在数学上表示为：

通过对平均过程的迭代，缩小了高资源节点和低资源节点之间的差距。注意，标准HC过程中的总资源是可变的，而标准MD过程中的资源总量是不变的。对于MD过程，资源将均匀地分配给它的邻居。与此相反，在HC过程中，通过平均化过程对资源进行重新分配，节点接收到的资源水平等于其相邻节点拥有的资源的平均数量。

2 迭代更新机制

本文构建一种混合更新机制，调节节点度对节点重要性的影响。结合节点度和节点介数中心性在标准MD 和HC 过程更新规则中的作用，通过适当调整权重参数，该混合更新机制对具有特定结构特征的关键节点具有良好的识别性能。连接矩阵A={aij}∈RN×N，当节点i和j是连接的时候aij=1，否则等于0，网络节点的迭代更新操作可以表示为：

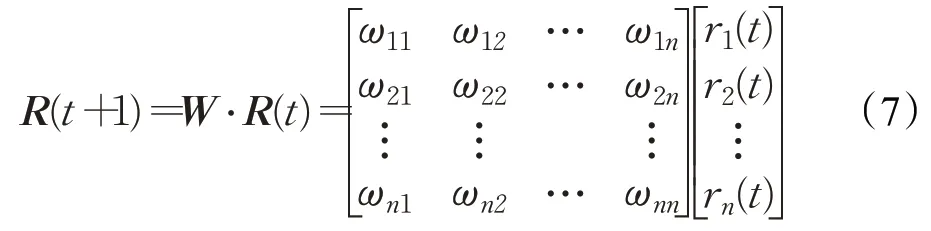
其中，R(t)是包含所有节点在第t步持有的排名分数的n维向量，W是转移矩阵，R(t+1) 是所有节点在第t+1步持有的分数。该公式定义了W等于连接矩阵A时特征向量中心性的更新机制。由于MD 过程将节点的资源均匀分布到其相邻矩阵中，因此MD过程对应的转移矩阵WM的元素可定义为：

其中，dj为节点j的重叠度数。HC过程通过最近邻平均化过程更新节点状态，因此HC过程对应的转移矩阵WH的元素可定义为：

为了使混合更新机制具体化并实现两个物理过程之间的平滑过渡，通过非线性混合机制将MD 和HC 过程结合起来，并将权重参数化纳入到过渡矩阵的归一化中。混合更新机制的转换矩阵WM+H定义为：

很明显，当λ=0 时退化为MD算法，当λ=1 时退化为HC算法（本文取λ=0.7）。基于转移矩阵WM+H，迭代更新操作可以重新表示为矩阵式为：

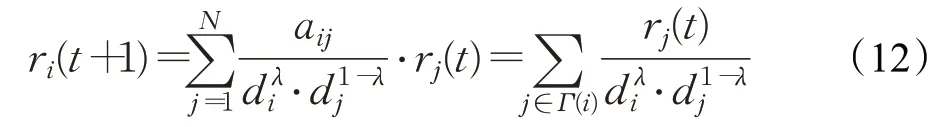
当节点之间之间存在一条边时，一个节点重新分配给它的邻居的资源与概率成正比。

3 算法核心

值得注意的是，本文所提出的混合更新机制避免了资源集中在几个高度节点上，使得一些有意义的低度节点也能被选择出来。在PIA 算法中，节点随机初始化，使用混合更新机制更新节点的排名得分，利用网络节点的稳定状态对节点进行排名。

算法PI Algorithm

有效的节点排序算法只需运行迭代规则即可得到正确的排序列表，而不需要最终收敛。因此，将PIA 的终点设在δt+1≈δt处，而不在R(t+1)≈R(t)处。当W的显性特征值和次显性特征值（分别为λ′和λ″）的绝对值不同且|λ′|＞|λ″|时，该算法收敛。收敛速度与是成正比的。在实践中，收敛通常很快发生。幂次迭代求解要求转移矩阵W是对称的，但即使存在条件较差的矩阵，幂次迭代求解也总是收敛的。

4 实验结果

比较了PIA 与IEP、RA、OD 和OB 在六个相互依赖网络（ER-BA、ER-WS、BA-BA、BA-WS、WS-WS）的差异。其中，RA 表示随机选取节点进行攻击的策略，OD表示选取节点度最高的节点进行攻击的策略，OB 表示选取节点重叠介数中心性最高的节点进行攻击的策略。在所有相互依赖的网络中，子网A中的每个节点都仅依赖子网B中的一个节点，反之亦然（如图2所示）。

子网络构建算法如下。

BA网络：

增长：初始化一个具有m0节点的完全连接图，并向网络中已有的多个节点添加m个新连接(m＜m0)。

连接：根据轮盘赌游戏添加连接。

ER网络：

初始化：给定N个节点和需要添加的边数M。

随机连接：随机选择一对没有内部连接的节点，在节点之间添加一条边；重复上述过程，直到在不同对节点之间添加了M个连接。

WS网络：

初始化：生成一个有N个节点的最近邻耦合网络，其中每个节点连接到其左右的各K/2 个节点。

重连接：以概率p随机重连接网络中的边缘。

为了比较不同拆除策略的效果，从网络平均节点度和网络总节点数两个角度评估相互依赖网络的鲁棒性。每条曲线是15次模拟的平均值。

G反映了相互依赖网络在最初出现故障后继续运作的能力，从图4～9中可以看出，在相互依赖的网络中，当相同数量的节点被移除以后，对比其他策略，PIA 的所对应G几乎都是最小的。从图9 中看出在某些特殊情况下，PIA 策略和其他策略效果类似。因此，可以得出在各种相互依赖的网络中，PIA策略优于其他策略。

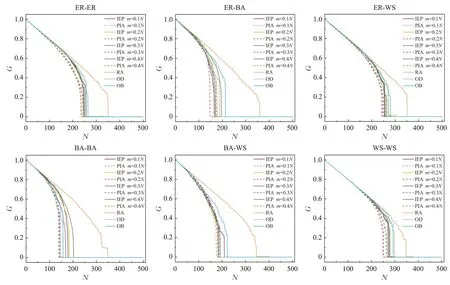
图4 去掉部分节点以后G的大小（N=500，子网络A的平均度等于8，B的平均度等于8）Fig.4 GMCC size after q fraction of nodes is removed

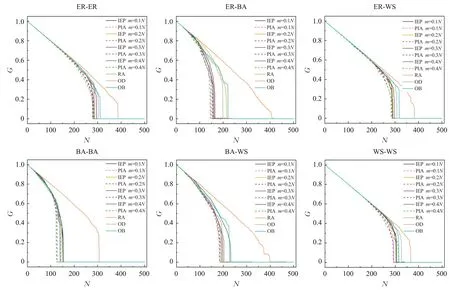
图5 去掉部分节点以后G的大小（N=500，子网络A的平均度等于10，B的平均度等于10）Fig.5 GMCC size after q fraction of nodes is removed

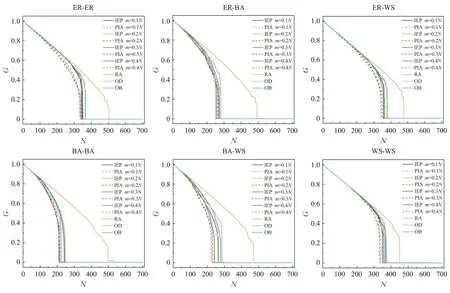
图6 去掉部分节点以后G的大小（N=700，子网络A的平均度等于8，B的平均度等于8）Fig.6 GMCC size after q fraction of nodes is removed

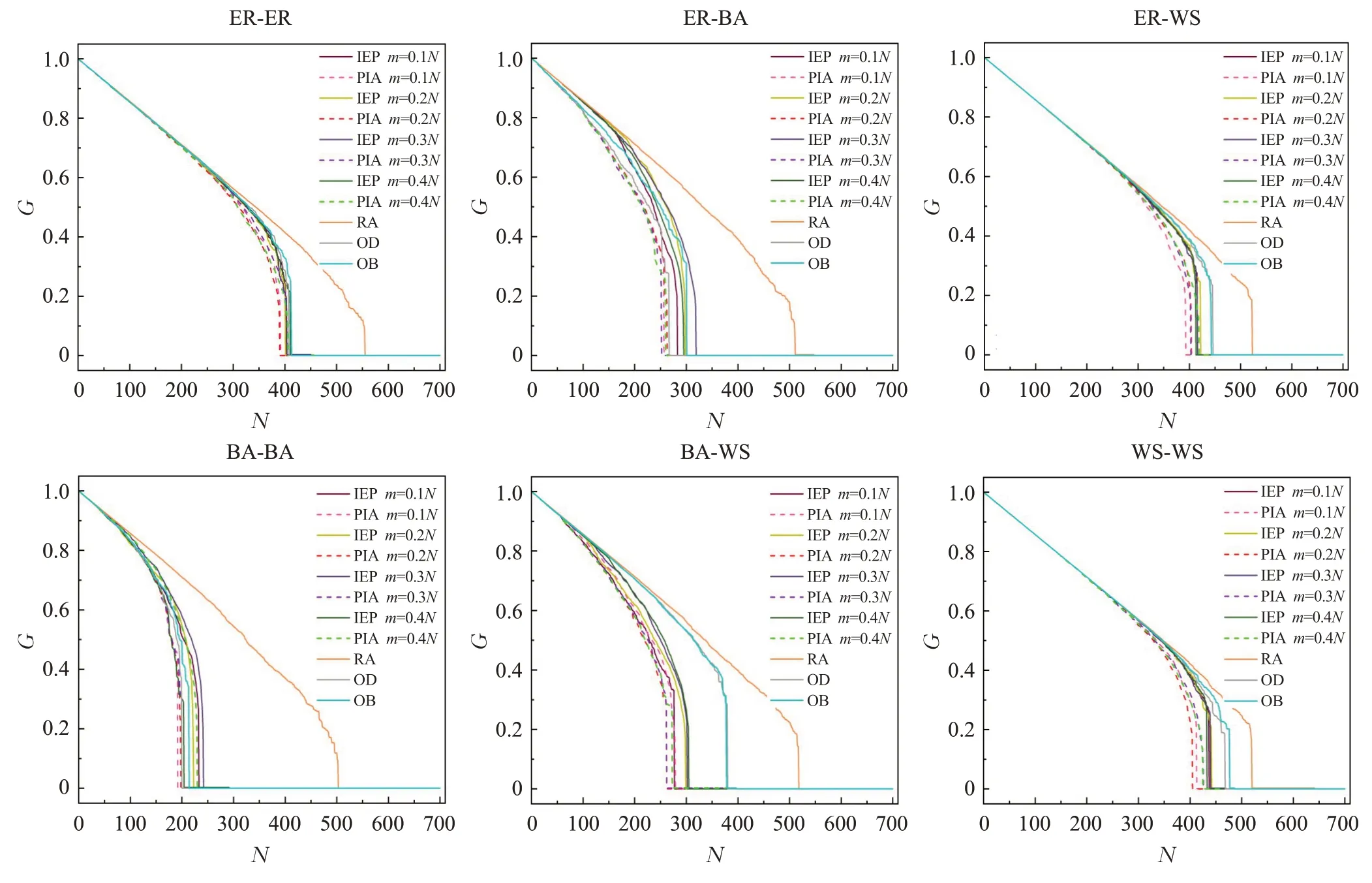
图7 去掉部分节点以后G的大小（N=700，子网络A的平均度等于10，B的平均度等于10）Fig.7 GMCC size after q fraction of nodes is removed

图8 去掉部分节点以后G的大小（N=1 000，子网络A的平均度等于5，B的平均度等于5）Fig.8 GMCC size after q fraction of nodes is removed

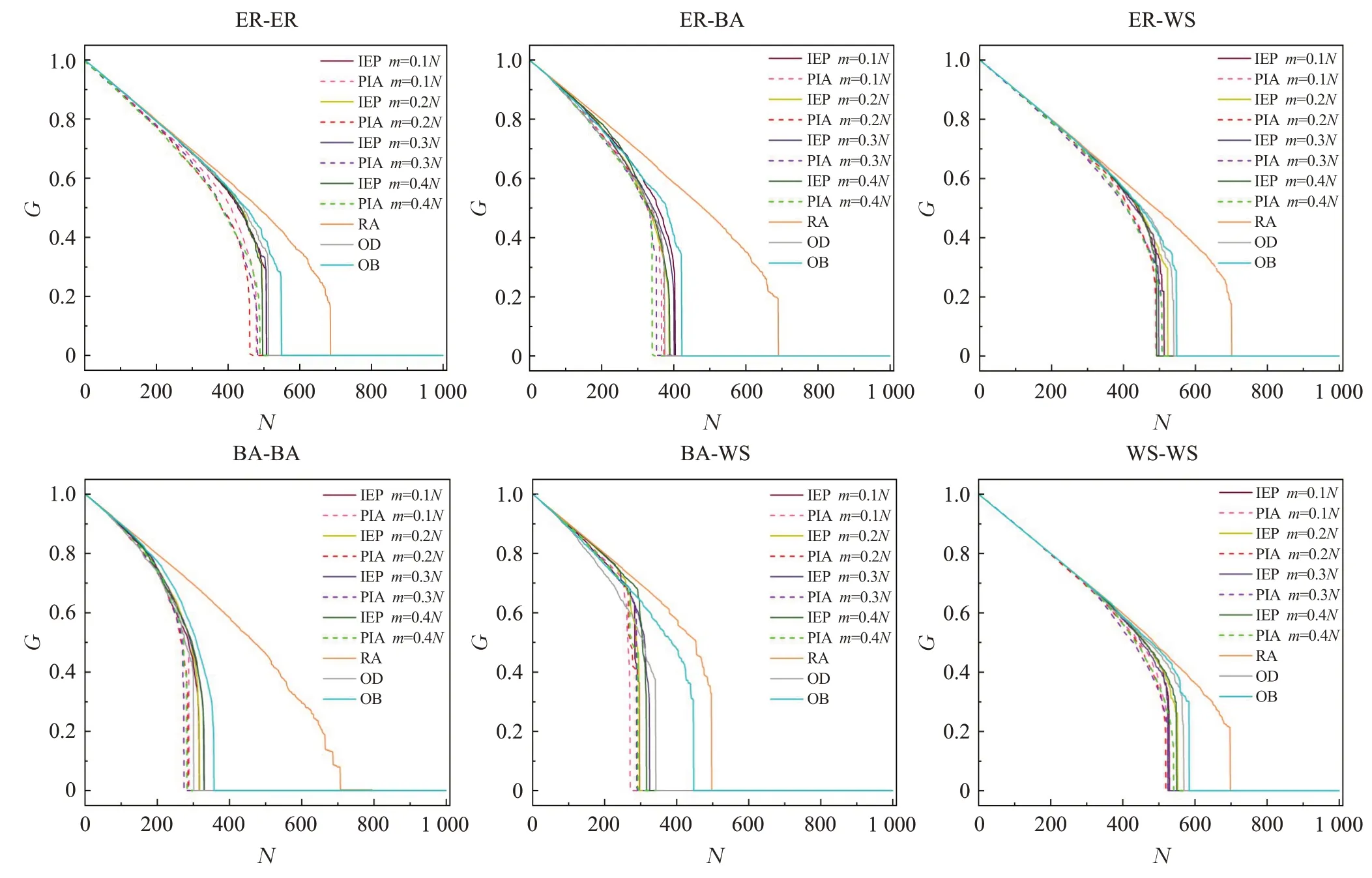
图9 去掉部分节点以后G的大小（N=1 000，子网络A的平均度等于8，B的平均度等于8）Fig.9 GMCC size after q fraction of nodes is removed

网络瓦解也对应于寻找移除节点的最小比例qc（q表示移除的节点占总节点比值），以确保G小于期望：

qc=ε表示在一串级联失效以后G的期望。

图10在六个不同的相互依赖网络上，采用4种不同的m的PIA 策略和其他策略的qc(ε=0)值。从图10 中可以得出结论，在所有网络中，每个策略中对于不同m，PIA策略的效果均处在最优的位置。在不同的策略下，几乎所有的PIA策略都比其他策略表现出更好的效率。此外，将算法应用在了一个真实世界中相互依赖的网络中，使用从2000年1月2日自治网络系统导出的子图和IEEE 118总线测试用例的电网，是一个具有118个节点的电力和互联网耦合网络。图11显示了去除不同的m个节点后相互依赖网络的GMCC大小，表1显示了各种策略下的qc。

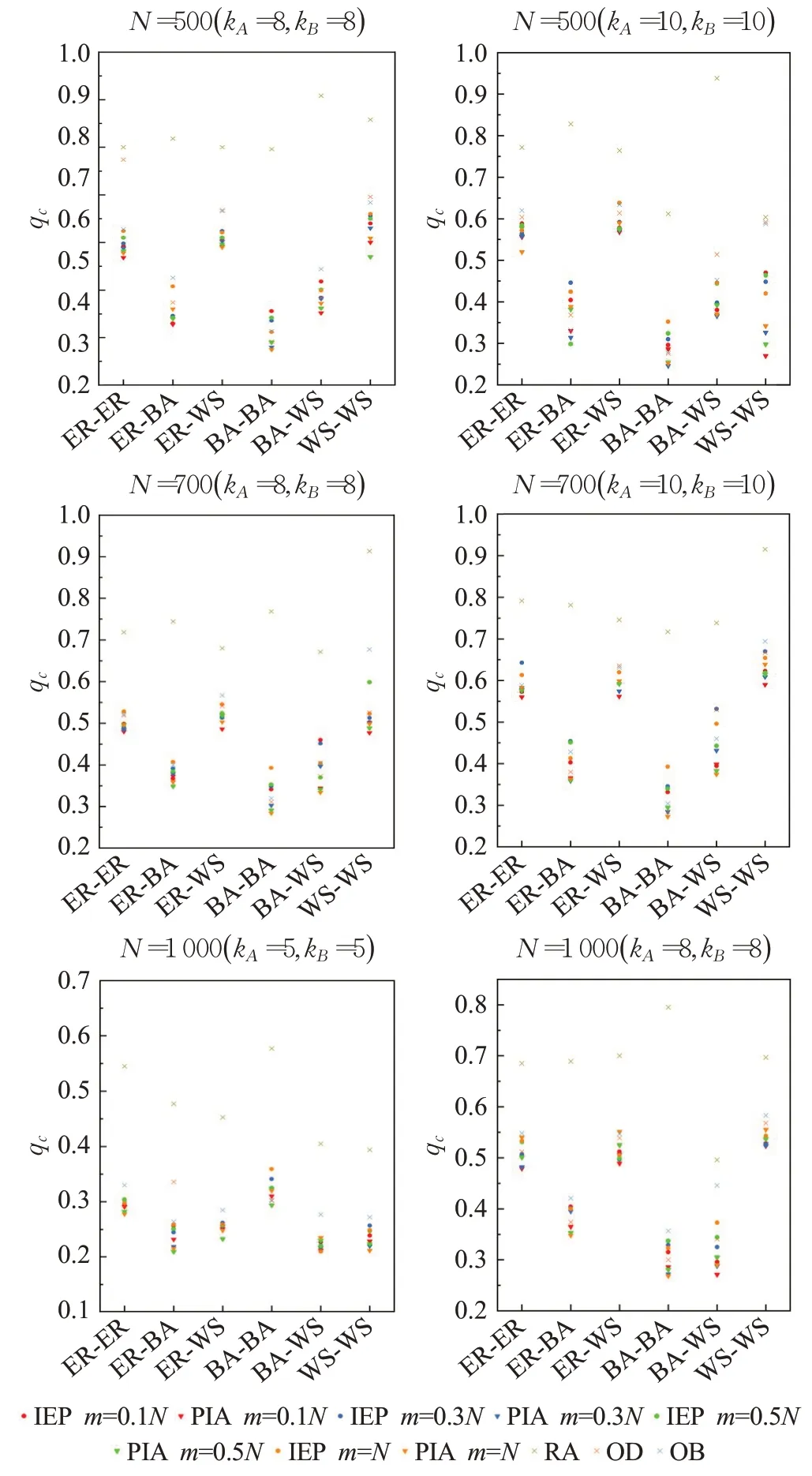
图10 不同策略对不同网络效果的对比Fig.10 Comparison of different strategies for different network effects

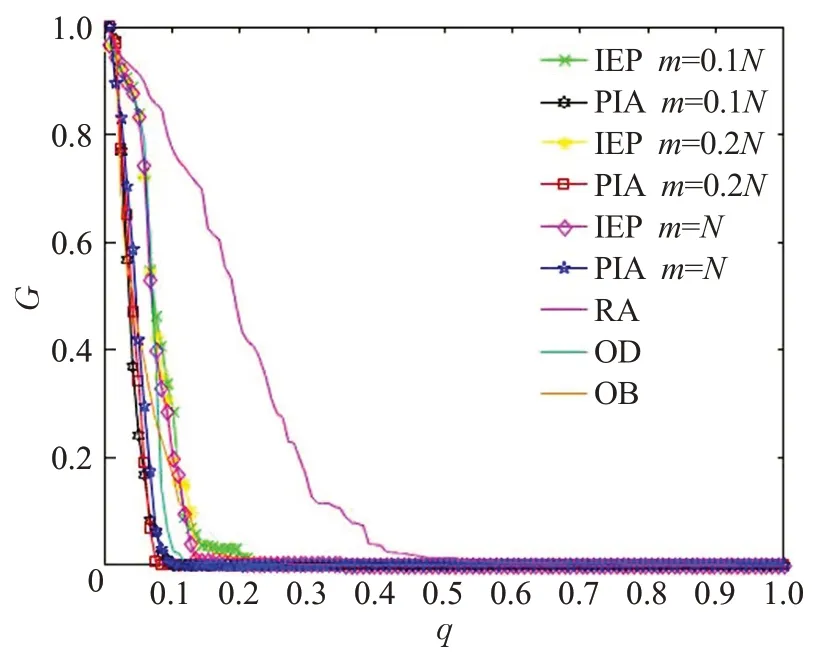
图11 去掉q 部分节点后各种策略真实网络的模拟效果图Fig.11 Simulation renderings of real networks with various strategies after removing part q nodes

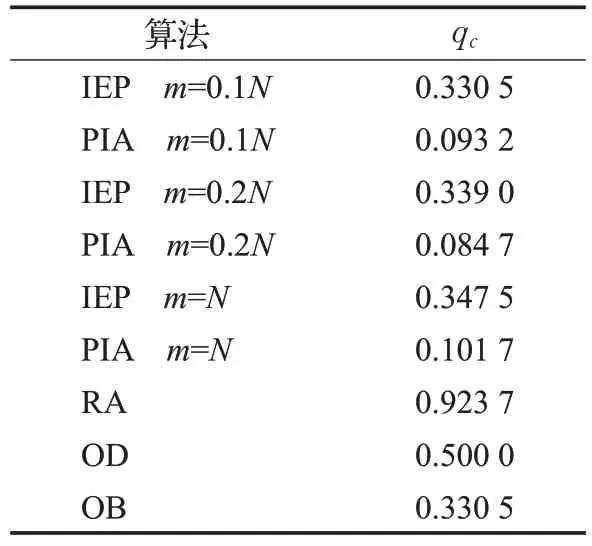
表1 各种策略下的的qcTable 1 qc under various strategies

根据模拟结果可以得出结论，PIA仍然比其他策略有更好的表现。

5 结语

在本文中，研究了相互依赖网络的最优解的问题，主要目的在于寻找去除这些节点后能使网络崩溃的最小节点集。提出了一种新的分解策略PIA，根据三个指标选择促进GMCC缩小最快的节点集。大量的仿真结果表明，在真实相互依赖网络和人工双层网络中，PIA策略的性能都优于IEP 和其他策略。但是本文只考虑非加权的相互依赖网络，由于成本的限制，现实网络往往都是加权网络。接下来将研究加权网络的结构，将权重作为节点特性的一部分来进行算法改进。