AdaSVRG：自适应学习率加速SVRG

吉 梦，何清龙

贵州大学 数学与统计学院，贵阳550025

理论上，深度学习问题可转化为求解如下数学中的一个有限和目标函数的最小化问题：

其中，ψi(·)表示第i个样本的损失函数（成本函数），ω表示可学习参数，n表示样本总量（通常n很大）。在深度学习问题中，基于一阶梯度信息的随机梯度法是求解问题（1）常用方法[1-8]。在基于一阶梯度信息的优化方法中，全梯度下降法（full gradient descent method，FG）是一种特殊的学习方法，其在每次迭代过程中利用全部样本的梯度信息进行参数更新[9]，参数更新方式为：

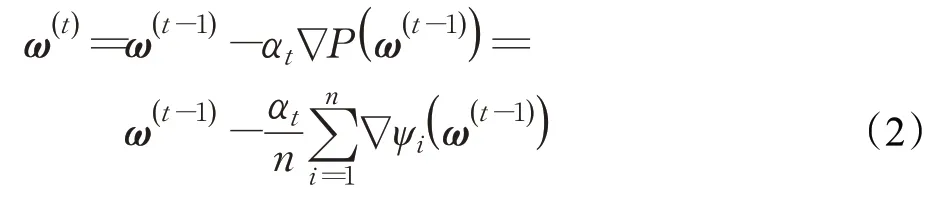
其中，t表示迭代步数，αt表示第t步迭代的学习率，∇表示梯度算子。FG 充分利用全部样本进行梯度估计，因此可以获得较好的下降方向，能够达到线性收敛速率[10-11]。然而，当训练样本过大时，FG 需要对所有样本进行梯度计算才能进行参数更新，因此，其计算量较大，阻碍了其在大规模学习中的应用[12-13]。此外，在深度学习任务中，样本数据常常具有冗余性，降低了FG的计算效率。

随机梯度下降法（stochastic gradient descent method，SGD）在每次迭代过程中只需计算一个样本的梯度[14]。因此，其每次迭代的计算量相对较小，其迭代格式为：

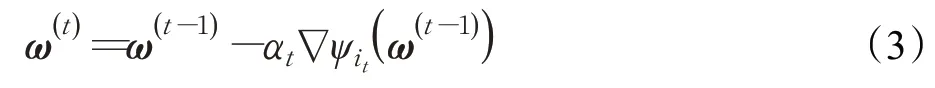
其中，it表示第t步迭代从{1,2,…,n}中随机选取的一个样本。SGD每次迭代只计算一个训练样本的梯度，大大降低了每次迭代的计算量。SGD 能快速收敛到一个可接受的解，但若想要得到更精确的解则需要更长的训练时间[15]。当部分样本数据存在较强的噪音时，由于SGD选取样本的随机性，导致SGD稳定性差、计算效率低。

小批量随机梯度下降法[16]（mini-batch stochastic gradient descent method，Mini-Batch SGD）充分利用FG和SGD各自的优点，即在每次更新参数时从全部样本数据中随机选取部分样本（称为一个小批量，记大小为|B|）进行梯度估计，因此，其参数更新方式为：

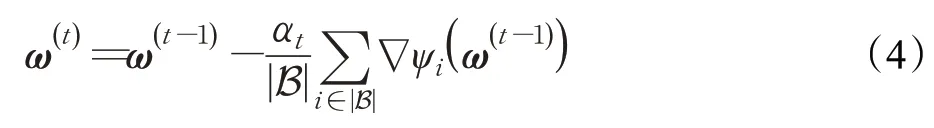
相比FG 来说，Mini-Batch SGD 在大规模学习任务上具有较高的计算效率。然而，Mini-Batch SGD 用一个小批量样本的梯度去近似整个训练集的梯度，梯度往往具有较高的方差，降低了Mini-Batch SGD 的收敛速度。针对随机梯度下降法中的高方差问题，通过对学习率进行衰减，以降低学习过程的震荡，但Mini-Batch SGD的收敛速度仍然较慢。

基于方差衰减的随机梯度法逐渐成为求解深度学习问题的研究热点，如随机平均梯度下降法[17]（stochastic average gradient method，SAG）、随机对偶坐标上升法[18]（stochastic dual coordinate ascent method，SDCA）及相关方法[19-22]。SAG、SDCA 等方法通过降低梯度的方差，从而达到对随机梯度下降法的加速。然而，SAG和SDCA在参数更新过程中均需要存储全部梯度（或对偶变量），对存储空间有较高的要求。随机方差衰减梯度法[23]（stochastic variance reduced gradient method，SVRG）克服了SAG和SDCA对大量存储空间需求的问题。SVRG的主要思想是：每隔m次参数更新计算一次全梯度，以降低存储需求，且该方法可以使用较大的学习率，具有较快的收敛速度。批量随机方差衰减梯度法[24]（mini-batch stochastic variance reduced gradient method，Mini-Batch SVRG）的提出弥补了SVRG 需要计算全梯度的不足，利用“小批量”计算量小的优点，即利用一个小批量样本的梯度去近似全梯度，避免了大计算量问题。

SVRG 和批量SVRG 在优化过程中均使用固定的学习率，当参数离最优点较远时，大的学习率能加快收敛速度；当参数离最优点较近时，若仍然采用大的学习率，可能会跳过最优点，导致学习过程在最优点附近震荡，降低收敛速度。此外，当之前的参数离当前参数较远时，当前参数离最优点越接近，此时SVRG 和批量SVRG 过多地利用历史梯度对当前梯度进行修正反而会造成学习过程震荡，降低算法收敛速度。针对固定学习率和过多使用历史梯度带来的学习过程震荡和收敛速度慢的问题，本文基于SVRG，利用学习率自适应的策略，并对下降方向进行加权平均，提出了自适应随机方差衰减梯度法（adaptive stochastic variance reduced gradient method，AdaSVRG）。基于MNIST和CIFAR-10数据集进行数值实验，以验证AdaSVRG方法的有效性。

1 AdaSVRG算法

在基于梯度信息的深度学习过程中，学习率和梯度是影响优化方法收敛速度的两个主要因素。因此，调整学习率和修正下降方向是提高优化方法收敛速度的两种策略[25]。FG对训练样本的充分使用能够准确估计梯度下降方向，但同时造成了计算成本过高的问题。Mini-Batch SGD 由于计算量小，不受训练集样本数量的影响，收敛速度快等优点，因此，常用于求解深度学习任务问题。然而，Mini-Batch SGD 常常伴随较高的梯度方差，使学习过程震荡大，降低了收敛速度。SVRG结合了FG 和SGD 的优点，在梯度估计时同时使用FG和SGD，通过降低梯度的方差，使得SVRG 具有较快的收敛速度。SVRG中使用FG进行梯度计算：

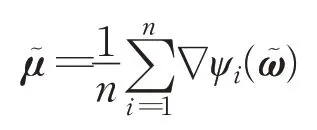
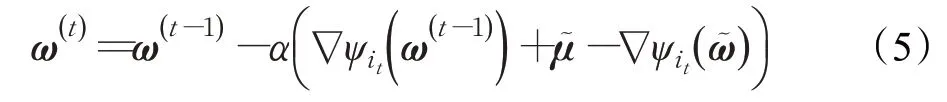
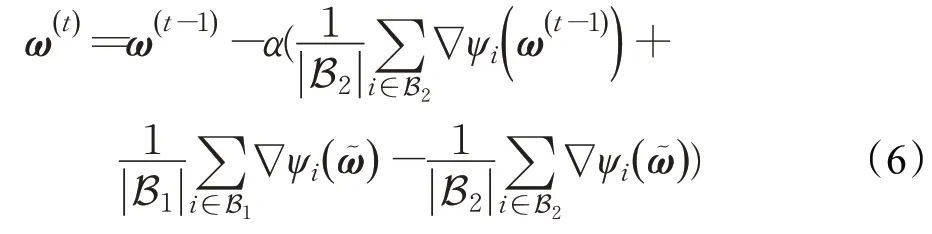
在式（6）中，使用小批量样本的梯度去近似全梯度时存在的误差会对训练精确度产生影响。文献[18]中指出，当批量SVRG 中的SGD 迭代没有采取小批量策略时，可以通过逐渐增加批量大小|B1|的方式来降低这个误差，并且当批量大小|B1|满足|B1|≥（S2为样本梯度范数的方差的上界，γ≥0，为常量）时，批量SVRG的收敛速率与标准SVRG的收敛速率相同。

在标准的梯度下降法中，每个参数在更新时都使用相同的学习率。由于每个参数的收敛速度都不相同，因此，根据不同参数的收敛情况分别设置不同的学习率，可以使得每个参数的更新尽量保持“同步”，从而达到对算法加速的目的。均方根传播法（root mean square propagation method，RMSprop）是由Tieleman 提出的一种自适应学习率方法[27]。其主要思想为设置初始学习率之后，每次通过初始学习率α逐参数地除以经过衰减系数β（本文中β=0.9）控制的历史梯度平方和的平方根，使得每个参数的学习率不同，达到学习率自动调节的作用，具体实现如下：

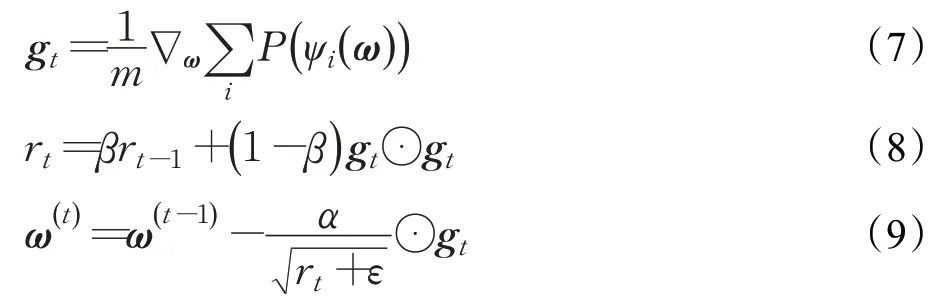
其中，⊙为按元素乘积，gt为第t次参数更新时的梯度，ε是为了保持数值稳定性而设置的非常小的常数，一般取值ε-7到ε-10。

自适应Delta法[28]（adaptive Delta method，AdaDelta）也是通过梯度平方的指数衰减移动平均来调整学习率，但还引入了每次参数更新差值Δω的平方的指数衰减移动平均，具体实现如下：

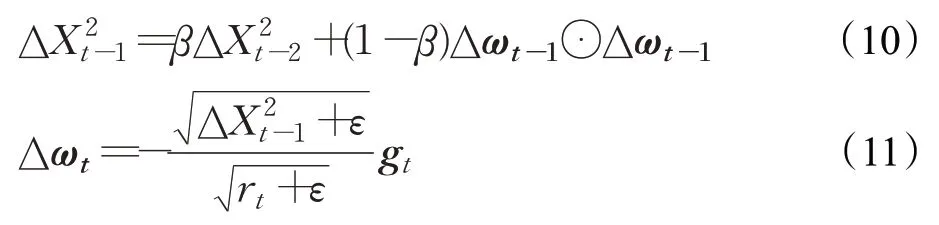
其中，rt的计算方式与式（8）相同。

自适应矩估计法[29]（adaptive moment estimation method，Adam）可以看作动量法与RMSprop 的结合，既使用动量作为参数更新方向，又采用RMSprop 自适应计算学习率的策略。具体实现如下：

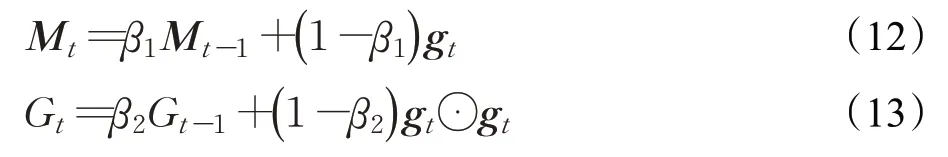
其中，β1和β2为不同移动平均对应的衰减率。Adam需要对Mt和Gt进行修正。即

Adam的参数更新差值为：

SVRG 和批量SVRG 使用的都是恒定的学习率，虽然可以使用较大的学习率来加快收敛速度，但较大的学习率可能会导致迭代不稳定甚至跳过最优值点，造成在最优值附近震荡的问题，反而降低了收敛速度。针对固定学习率造成的学习过程震荡问题，本文将RMSprop中的自适应学习率策略引入到批量SVRG 中。提出了学习率自适应的AdaSVRG。AdaSVRG 与RMSprop、AdaDelta、Adam 等算法的不同之处在于：AdaSVRG 在自适应调整学习率时应用的是方差衰减的梯度估计。如算法1所示。

在AdaSVRG 中，第8 步为批量SVRG 梯度平方的指数加权平均，用于自动调整每个参数的学习率，降低学习过程的震荡，提高收敛速度。第9 步中AdaSVRG相较于批量SVRG的改进之处在于：对第7步中计算梯度的式子采用加权平均来估计AdaSVRG 的下降方向，提高算法的稳定性。在批量SVRG 中，由于μs和ωs需要经过m次迭代后才更新一次，而ωt在这m次迭代中已经逐渐接近最优值ω*，故ωs与ωt-1之间的差异在这m次迭代中逐渐增大。因此，若过多采用参数为ωs时的历史梯度来对当前梯度（此时参数为ωt-1）进行修正，反而使得梯度估计变差，导致学习过程产生震荡。针对这一问题，AdaSVRG通过对梯度估计采用加权平均策略，使得当前的梯度估计既可以利用上历史梯度信息，又避免了因过多使用历史梯度信息进行修正带来的问题。因此，AdaSVRG具有更好的稳定性和更快的收敛速度。

2 收敛性分析

本章分析AdaSVRG 算法的收敛性。在本文中，如无特殊说明，表示实欧式空间中的内积，‖·‖均表示2-范数。假设ψi(ω)光滑且凸，∇ψi(ω)为L-Lipschitz连续函数，P(ω)为μ-强凸函数。假设‖ωt-ω*‖≤Z，Z≥0，对所有的t成立。假设μs近似全梯度时的误差为es。定义函数：

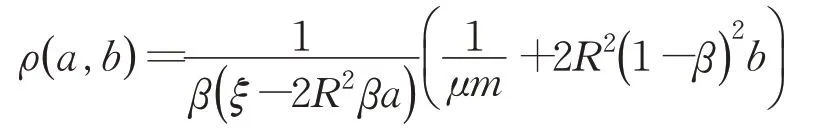
记ρ(L,L)=ρ，本文讨论a=b=L时的特殊情况。

定理1若μs=∇P(ωs)+es，设‖gt‖≤G，≤R，选取α、β、m、ξ使得0＜ρ＜1，则AdaSVRG 算法在option II下，满足：

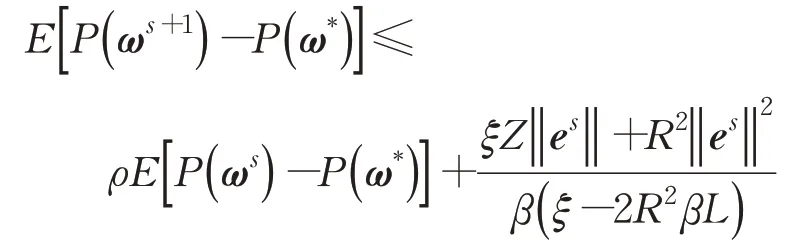
由定理1 可知，当误差es以一定的速率减小时，AdaSVRG算法收敛。

在给出定理1的证明之前，先介绍如下几个相关引理。以下证明中假设ω*为最优值。

引理1∀ω，有：

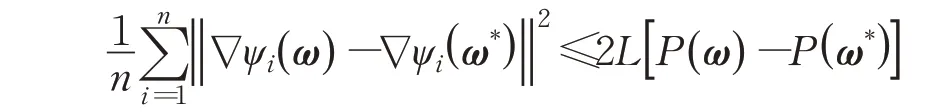
证明由于∇ψi(ω)为L-Lipschitz连续函数，满足：

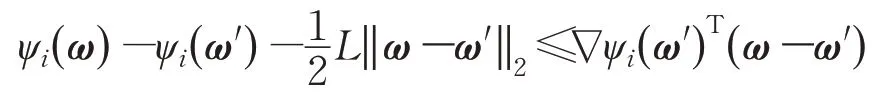
令ω′=ω*，对不等式在所有i上求和后两端乘以可得引理1。

证毕。

引理2∀a，b，c∈Rn，若＞0 且b所有分量为正，则存在ξ＞0，使得：

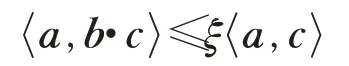
证明由Cauchy-Schwartz不等式可知：

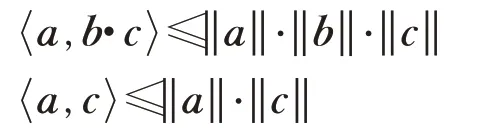
因此，存在ξ＞0，η≥‖b‖＞0，使得：

即存在ξ＞0，使得：

证毕。

用νt表示第t步时的搜索方向，即：

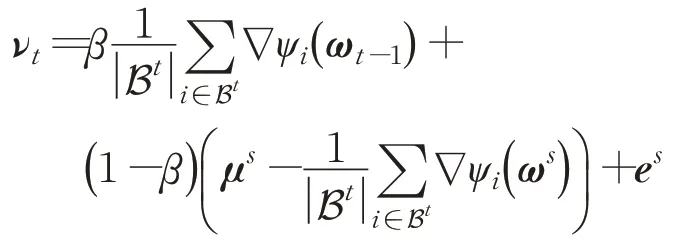
可得：

E[νt]=β∇P(ωt-1)+es

引理3在参数更新的内循环中，对第t次迭代成立：

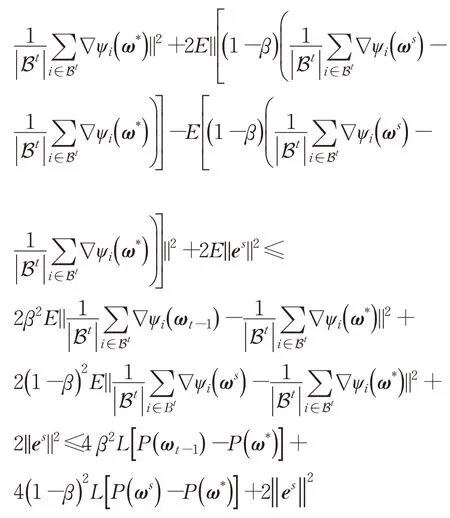
证毕。

引理4在参数更新的内循环中，设‖gt‖≤G，对第t次迭代成立：

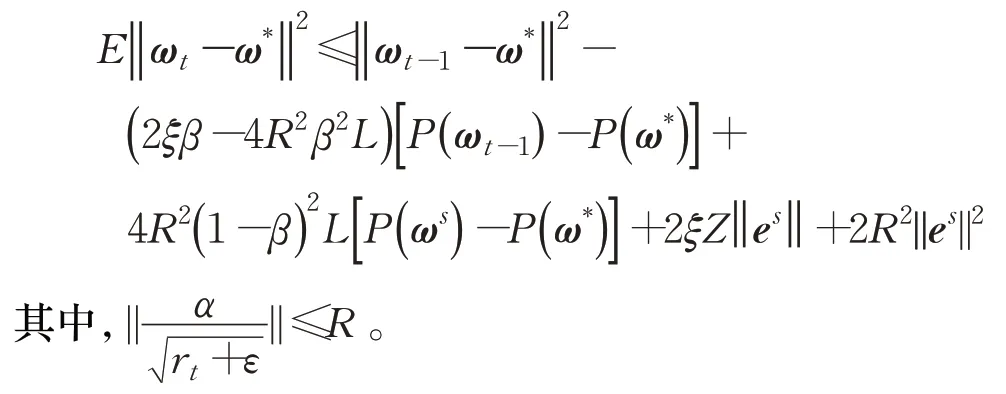
证明由于‖gt‖≤G，故存在R＞0，使得≤R，由引理2、引理3 以及AdaSVRG 算法的迭代规则ωt=ωt-1-，可得：

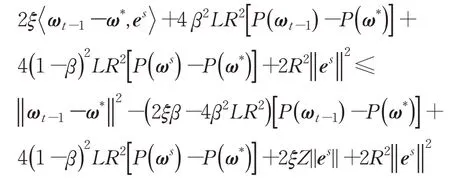
第一个不等式根据引理2 所得，由于-νt为参数更新方向，因此＞0。第二个不等式根据引理3所得。第三个不等式根据P(ω) 的凸性，即满足不等式-(ωt-1-ω*)T∇P(ωt-1)≤P(ω*)-P(ωt-1)，第四个不等式利用了Cauchy-Schwartz 不等式和‖ωt-1-ω*‖≤Z。证毕。

为了证明定理1，将引理4 中的不等式对所有t=1,2,…,m相加后求期望，可得：

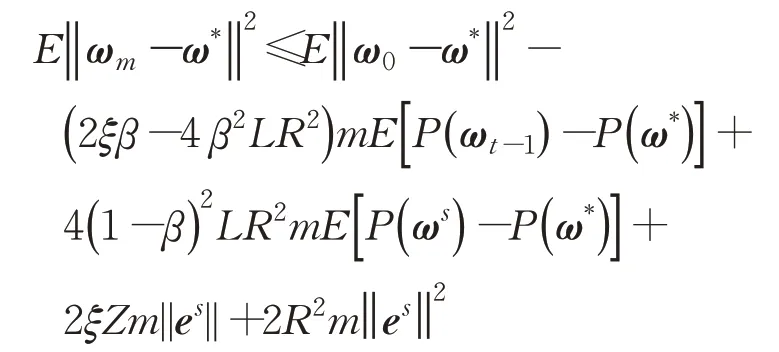
对固定的第s次循环，记ω0=ωs，E[P(ωt-1)]=E[P(ωs+1)]，对AdaSVRG算法option II可得：

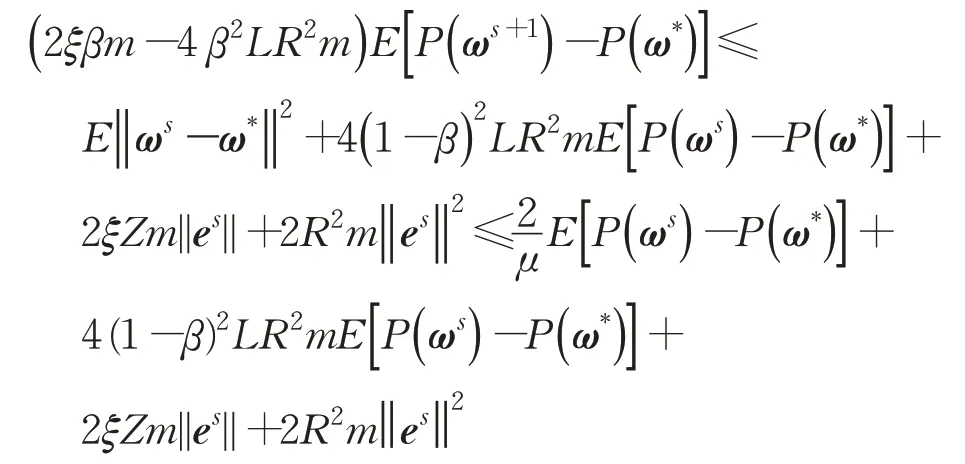
第二个不等式根据P(ω)的μ-强凸性质，即满足P(ω)-P(ω′)-≥∇P(ω′)T(ω-ω′)且∇P(ω*)=0。由于0＜ρ＜1，故2ξβm-4β2LR2m＞0，则有：

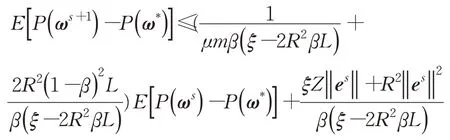
证毕。

3 数值实验分析

3.1 MNIST数据集

为了验证AdaSVRG的有效性，本章基于MNIST和CIFAR-10 数据集分别进行数值实验。为了公平起见，批量SVRG算法中，全梯度也采用小批量进行近似。通过比较AdaSVRG 与Mini-Batch SGD、批量SVRG 对同一数据集及网络的表现来说明AdaSVRG在收敛速度上的优越性。实验中对不同的数据集使用了不同的训练网络，MNIST 数据集使用网络N1（3 层全连接层，激活函数为ReLU 函数），CIFAR-10 数据集使用网络N2（ResNet 网络）。关于实验数据集的具体说明见表1。为了避免实验的偶然性，对所有数据集均在相同条件下进行了三次同等重复实验，下文中所有数据均取三次重复实验的平均值。

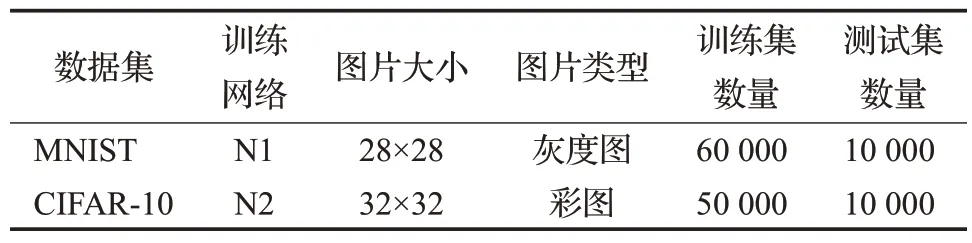
表1 数据集及对应训练网络说明Table 1 Description of data sets and training networks

实验参数说明：iteration_times=10 000，表示网络训练次数；α=0.01，表示初始学习率；lg_batch为近似全梯度的批量大小；batch_size表示AdaSVRG中方差衰减的Mini-Batch SGD迭代的批量大小和Mini-Batch SGD的批量大小；m为AdaSVRG 中进行方差衰减的Mini-Batch SGD迭代的次数。

由表2、表3、表4可知，对于MNIST数据集，同一条件下，由于AdaSVRG需要自适应计算学习率，因此其所用的训练时间在三者中最长，但AdaSVRG 在训练集和测试集上的精确度也是三者中最高的，相较于批量SVRG 和Mini-Batch SGD 来说，AdaSVRG 在训练集和测试集上的精确度提升明显。同一条件下，批量SVRG在训练集、测试集上的精确度低于Mini-Batch SGD。随着batch_size的增大，三种方法在训练集和测试集上的精确度都有微小的提高，但伴随着训练时间也在增加。因此，在MNIST 数据集上，若想进一步使用AdaSVRG提高训练集和测试集的精确度，可在增加训练时间为代价的情况下，适当增大batch_size。若想降低AdaSVRG的训练时间，使用较小的batch_size 也能在训练集和测试集上达到理想的精确度。

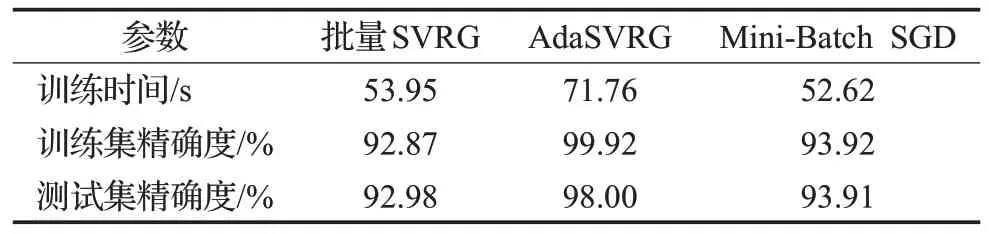
表2 实验参数（lg_batch=1 000，batch_size=100，m=10）Table 2 Experiment parameters

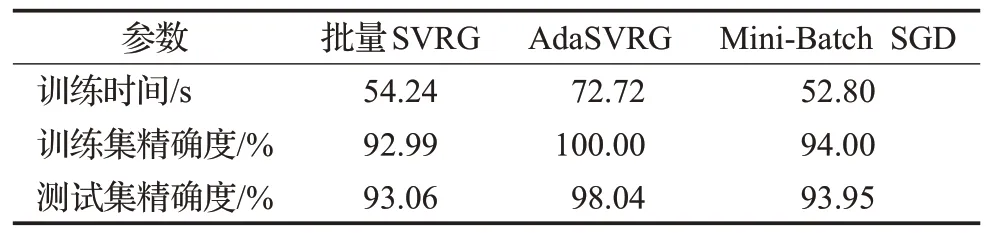
表3 实验参数（lg_batch=1 000，batch_size=300，m=10）Table 3 Experiment parameters

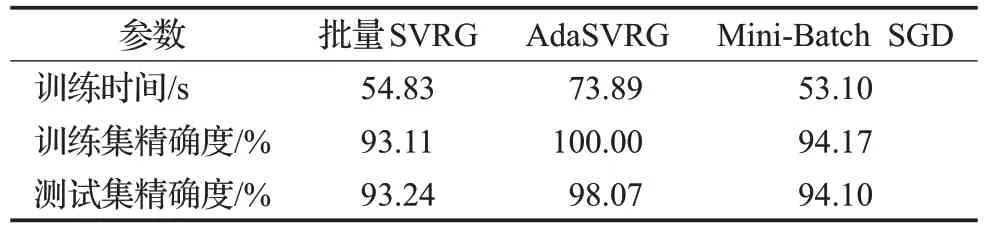
表4 实验参数（lg_batch=1 000，batch_size=500，m=10）Table 4 Experiment parameters

由表3、表5 可知，在MNIST 数据集上，同等条件下，若增大m，AdaSVRG 的学习效果仍然优于批量SVRG。并且，增大m后，AdaSVRG在测试集上的精确度有小幅提高，并且AdaSVRG 的训练时间也有微小减少，说明适当增大m可以节省AdaSVRG训练时间。然而，随着m的增大，更新参数的梯度估计变差，会使学习效果变差。如在m增大后，AdaSVRG在训练集上的精确度有所降低。

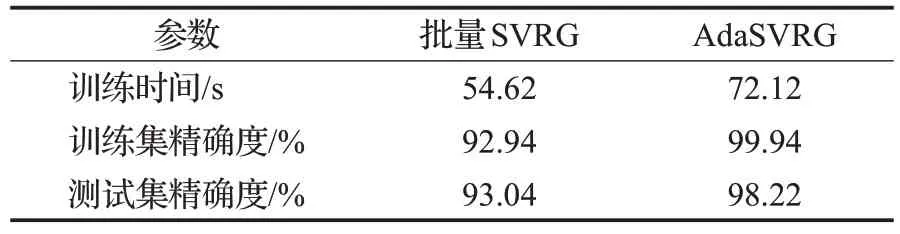
表5 实验参数（lg_batch=1 000，batch_size=300，m=50）Table 5 Experiment parameters

由图1 可知，AdaSVRG 在MNIST 数据集上的收敛速度明显优于批量SVRG和Mini-Batch SGD。AdaSVRG在学习过程中的震荡程度明显降低，并且在训练达到一定次数后，Loss的值便开始趋于稳定不再下降。

图1 MNIST数据集收敛过程图Fig.1 Convergence process of MNIST data set

3.2 CIFAR-10数据集

由表6、表7、表8可知，由于ResNet网络的复杂度高，因此AdaSVRG 在CIFAR-10 数据集上所需的训练时间较长，但对训练集和测试集精确度的提升比批量SVRG和Mini-Batch SGD明显。在同等条件下，AdaSVRG在测试集上的精确度比批量SVRG和Mini-Batch SGD最多分别高出了15.7个百分点（见表7）、16.6个百分点（见表8）。Mini-Batch SGD在一定条件下的学习效果甚至优于批量SVRG（见表6、表7）。

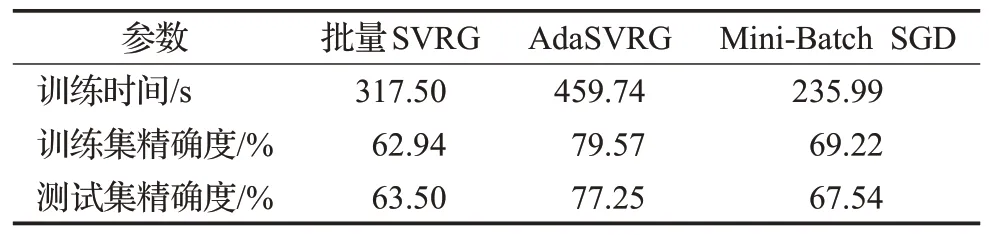
表6 实验参数（lg_batch=1 000，batch_size=100，m=10）Table 6 Experiment parameters

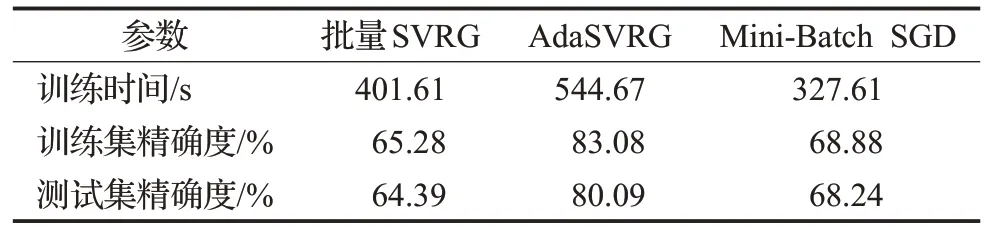
表7 实验参数（lg_batch=1 000，batch_size=300，m=10）Table 7 Experiment parameters

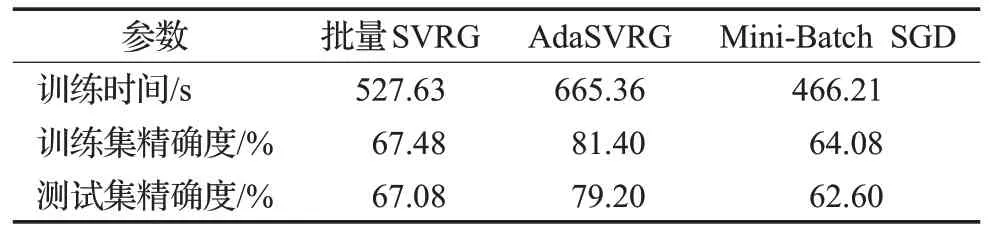
表8 实验参数（lg_batch=1 000，batch_size=500，m=10）Table 8 Experiment parameters

由表7、表9 可知，在CIFAR-10 数据集上，增大m后，批量SVRG 和AdaSVRG 的训练时间都有不同程度的减少，但批量SVRG 的训练集和测试集精确度降低，而AdaSVRG有微小的提高。

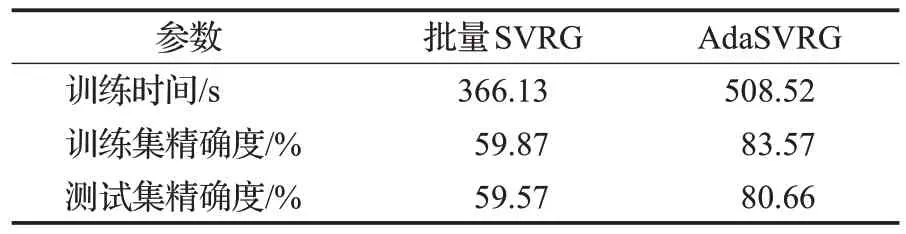
表9 实验参数（lg_batch=1 000，batch_size=300，m=50）Table 9 Experiment parameters

由图2 可看出，AdaSVRG 在CIFAR-10 数据集上的收敛速度同样优于批量SVRG 和Mini-Batch SGD，学习过程的震荡大幅降低。并且AdaSVRG 在CIFAR-10数据集上训练达到一定次数后，Loss曲线也开始趋于稳定不再变化。

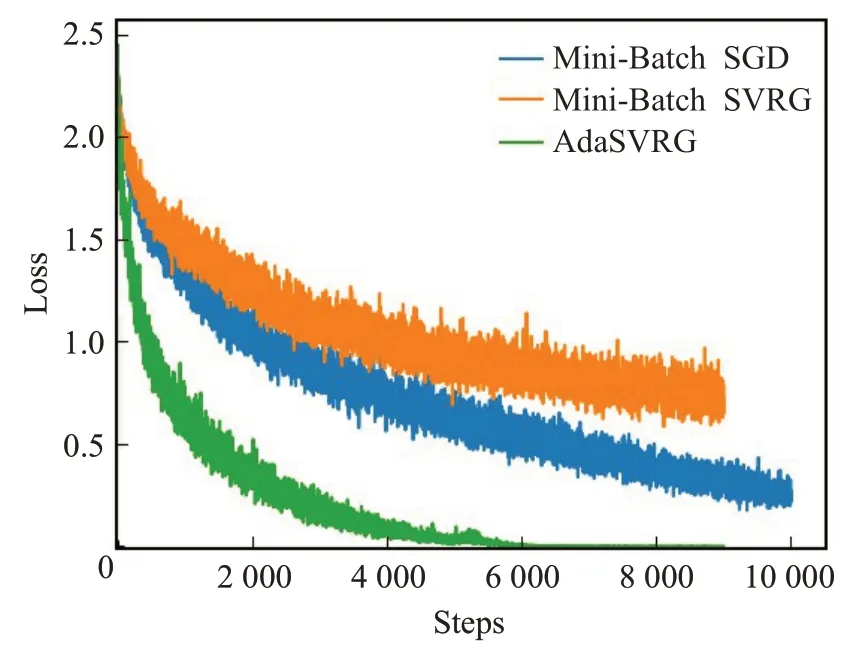
图2 CIFAR-10数据集收敛过程图Fig.2 Convergence process of CIFAR-10 data set

4 总结

本文通过对批量SVRG采取自适应学习率的策略，以及对梯度估计采取加权平均的思想，使得AdaSVRG在学习率和梯度估计修正方面都进行了改进。实验结果表明AdaSVRG 在收敛速度和训练集、测试集上的准确率等方面均优于批量SVRG和Mini-Batch SGD，并克服了批量SVRG 中因使用固定学习率和过多使用历史梯度对当前梯度进行修正所带来的问题，同时克服了Mini-Batch SGD在迭代中由于梯度估计随机性产生的高方差问题。由于AdaSVRG有较好的学习率和梯度估计，因此AdaSVRG 稳定性高，学习过程震荡小，收敛速度快。在训练相同的次数时，虽然AdaSVRG 在迭代时需要自适应计算学习率会导致训练网络所需要的时间相对较长，实验证明可以通过适当降低AdaSVRG 中使用的Mini-Batch SGD 的批量大小、适当增大m的值以及适当减少训练次数等方法来降低AdaSVRG的训练时间。相较于标准SVRG和批量SVRG，AdaSVRG额外引入了一个超参数系数β，因此，如何选取超参数的值对提高AdaSVRG的计算效率非常有意义。