基于盒维数的灵巧噪声干扰识别方法
李杰然
( 91404部队,河北秦皇岛 066200)
雷达作为预警探测的主要装备,在现代战争中有着举足轻重的地位,它是决定战争胜利的重要因素之一。为了限制雷达探测能力发展,雷达干扰技术应运而生,特别是数字射频存储(DRFM)和直接数字频率合成(DJS)等技术的应用,使得雷达干扰技术迅速发展。灵巧噪声干扰是1 种作用于现代雷达的先进干扰技术,因其兼具压制干扰和欺骗干扰的双重特点,使得雷达抗干扰面临更高的挑战。
为了有效对抗灵巧噪声干扰,准确的识别干扰是采取针对性抗干扰措施的关键。目前,在干扰识别研究中,国内外学者已经做了大量工作。文献[3]针对欺骗式干扰提出了1种基于双谱特征和模式识别技术的干扰识别方法;文献[4]提出了1种基于信号包络起伏参数,相位门限内概率及盒维数等多维特征联合处理的灵巧噪声干扰识别方法;文献[5]将熵作为干扰信号的特征,提出了1 种基于熵理论的间歇采样转发干扰识别方法;文献[6]针对转发式欺骗干扰,提出了1 种基于拟合优度的欺骗干扰识别方法。随着信号处理技术的发展,干扰识别方法也在不断创新,但仍欠缺针对性强、多样的灵巧噪声干扰识别的研究。
本文从灵巧噪声干扰产生机理出发,重点分析了卷积调制、数字多时延和间歇采样转发3 种灵巧噪声干扰的信号特性,提取信号盒维数作为特征参数,利用支持向量机对目标与干扰信号进行分类识别,通过蒙特卡洛方法仿真验证了识别结果。
1 信号模型
假设雷达发射信号()为线性调频信号


则,采样信号为:

2 频谱特征分析

对式(7)做傅里叶变换可得间歇采样转发干扰信号频谱()为:
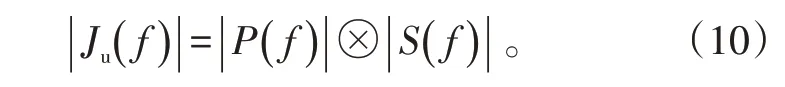
如果雷达信号脉冲宽度为20 μs ,调频带宽为5 MHz,载波频率为2 MHz,可仿真目标回波信号频谱如图1 所示。设卷积视频信号()为均值0,方差为1的高斯白噪声,仿真卷积调制干扰频谱,如图2 所示。设数字多时延干扰的延迟时间为0.6 μs,为30,则其频谱,如图3 所示。设间歇采样转发干扰信号的采样周期为2.5 μs,采样占空比为0.4,则其频谱,如图4所示。对比目标回波信号和3种干扰信号的频谱可以发现,3 种干扰信号频谱与目标回波信号频谱宽度和位置基本相同,但干扰信号频谱带宽内起伏更加不规则和复杂。因此,可以利用带宽内频谱的差异进行干扰信号的识别。
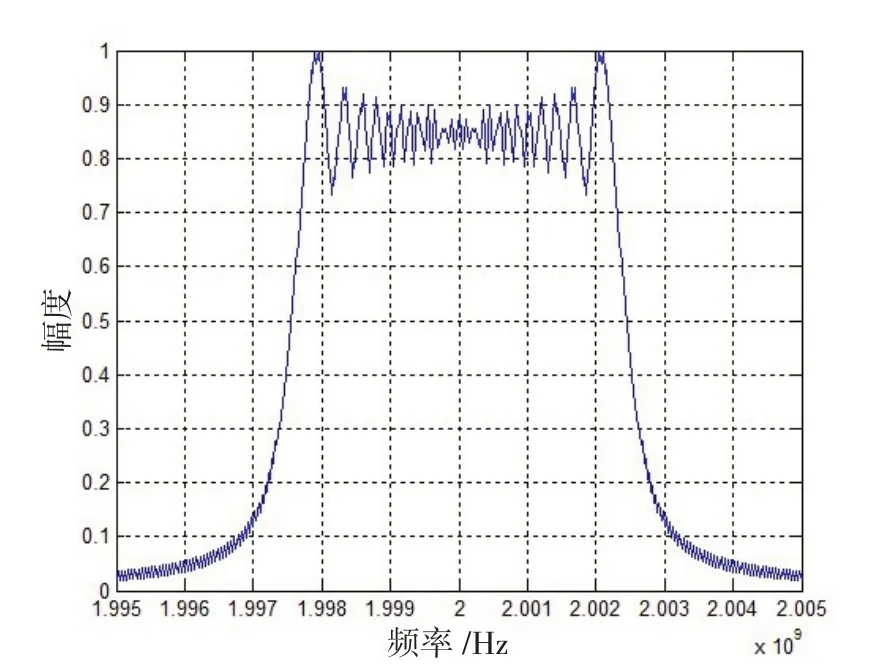
图1 目标回波信号频谱Fig.1 Spectrum of target echo signal
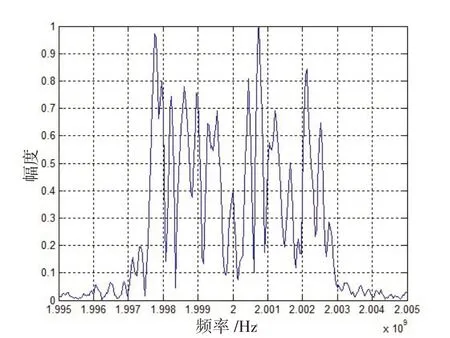
图2 卷积调制干扰信号频谱Fig.2 Spectrum of convolutional modulation jamming signal

图3 数字多时延干扰频谱Fig.3 Spectrum of digital multidelay jamming signal
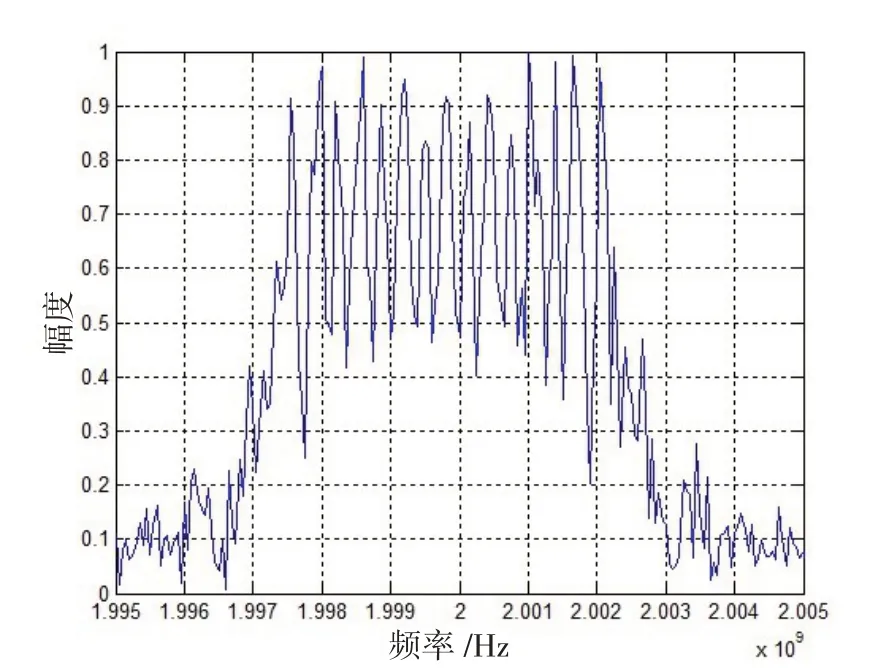
图4 间歇采样转发干扰信号频谱Fig.4 Spectrum of intermittent sampling repeater jamming signal
3 特征选取
由上一节分析可知,3 种干扰信号频谱存在一定相似性,与目标回波信号相比,频谱更加复杂。根据这一特征,本文尝试将分形理论应用到干扰识别中。分形维数可以定量描述分形集的复杂性,而盒维数可以定量描述分形集的几何维数,因此,利用分形盒维数作为信号特征可以区分干扰信号。参考文献[16-18]给出的盒维数简化形式,设信号序列为{(),=1,2,…,},其盒维数的计算方法为:将信号序列{()}放置于单位正方形内,横坐标的最小间隔为=1,设
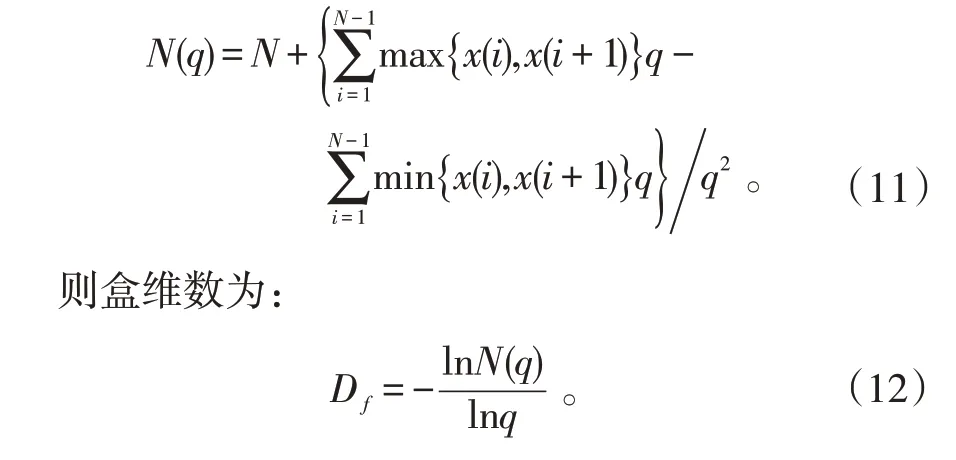
4 仿真验证
为了检验分形盒维数作为干扰信号特征参数的有效性,设置仿真条件如下:设雷达发射信号为线性调频信号,载频为2 GHz ,带宽为5 GHz ,脉宽为20 μs,卷积视频信号()为均值为0、方差为1的高斯白噪声,数字多时延干扰信号的延迟时间为0.6 μs,间歇采样转发干扰信号的采样周期为2.5 μs,采样占空比为0.4。信噪比从-5 dB 到25 dB。在干信比为0 dB、5 dB 和10 dB 条件下,对每种干扰信号做300次蒙特卡罗仿真,计算各信号的频谱盒维数均值,结果如图5~7所示。
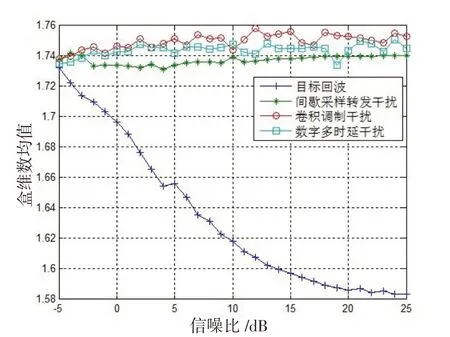
图5 盒维数均值(干信比为0 dB)Fig.5 Mean of box dimension(JSR=0 dB)

图6 盒维数均值(干信比为5 dB)Fig.6 Mean of box dimension(JSR=5 dB)
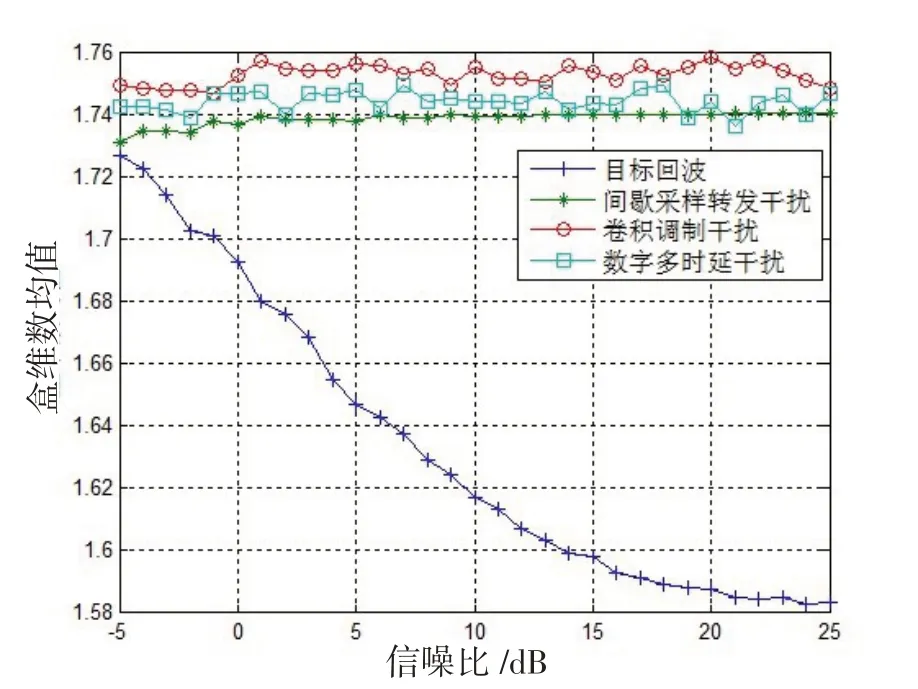
图7 盒维数均值(干信比为10 dB)Fig.7 Mean of box dimension(JSR=10 dB)
对比图中可以看出:一是随着干信比和信噪比的变化,干扰信号的盒维数均值变化较小,具有稳定的特征;二是目标回波信号的盒维数均值随信噪比增加逐渐变小;三是干扰信号的盒维数均值与目标回波信号的盒维数均值存在明显差距,且随着信噪比的增加差异逐渐增大,具有较好的分辨性。因此,采取信号盒维数作为识别特征是可行的。
在验证了盒维数特征的有效性后,本文利用支持向量机算法对3 种信号进行分类识别,分类器采取径向基核函数设计。在干信比为0 dB 条件下,信噪比为-5 dB 到25 dB 时选取150次仿真数据作为训练样本,剩余的150次仿真数据作为测试样本,其识别准确率,如图8所示。
从图8 可以发现,3种干扰信号的识别效果相当,且识别准确率随信噪比的增加而提高。当信噪比大于6 dB 时,干扰信号的识别准确率大于90%;当信噪比大于11 dB 时,干扰信号的识别准确率接近100%。因此,在实际使用中,按照识别准确率为90%以上的要求,信噪比只需满足大于6 dB 即可。
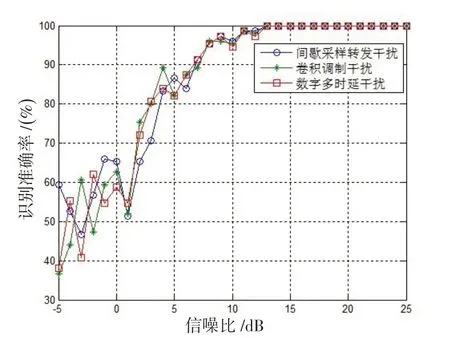
图8 各干扰信号识别准确率(干信比为0 dB)Fig.8 Recognition accuracy of jamming signals(JSR=0 dB)
5 结束语
本文针对卷积调制、数字多时延和间歇采样转发3 种灵巧噪声干扰信号识别问题,基于分形理论提出了将信号频谱盒维数作为特征的识别方法。通过仿真实验,验证了目标回波信号与干扰信号频谱盒维数的差异性。采用径向基核函数设计的支持向量机分类器对干扰信号进行了识别检验。仿真实验表明,该方法具有较高的识别准确率,能够区分本文研究的3种灵巧噪声干扰与目标回波信号。

