基于极限学习机的修正当前统计模型跟踪算法
张 霆
(南京电子技术研究所,江苏南京 210039)
由于运动模型或者参数的变化难以先验估计和预测,使得机动目标跟踪成为目标跟踪领域的难点和重点。常用的机动跟踪补偿思路为通过调整目标过程噪声矩阵对滤波增益进行修正,从而提高跟踪精度,如Singer 模型和当前统计(Current Statistical,CS)模型。CS模型算法通过修正瑞利分布描述目标加速度特性,实现加速度分布的实时修正,较之Singer模型更加符合实际情况。
目前,由于先验知识的匮乏,对目标的机动频率和加速度极值难以准确估计,影响了利用CS 模型对目标的建模。另外,CS模型在目标加速度较小时过程噪声大,使得算法对弱机动目标的跟踪效果有所减弱。
针对CS 模型存在的上述缺陷,许多学者对其进行了研究改进,并取得了较好的效果。文献[7]通过模糊函数对CS 模型的机动频率、加速度以及其方差进行自适应调整后,较为全面地提高了CS 的自适应能力;文献[8]通过新息对机动频率以及通过加速度增量和位置关系对加速度上限进行自适应调整,提高了CS模型的精度;文献[9]通过指数函数以及滤波残差,分别对机动频率和协方差进行修正,从弱、强机动2个方面提高了CS模型的性能;文献[10]使用新息对加速度极值进行自适应估计,并根据机动对新息协方差进行修正,从而修正了滤波增益,提高了机动时的跟踪精度;文献[11]通过机动检测,减少了CS 模型的动态时延,提高了对突发机动目标的跟踪性能。
然而,上述的改进方式均存在1个问题:对加速度或者其极值的自适应函数都是通过“经验”指定的,并且引入了外部参数,而外部参数也需要先验信息。如文献[12]自适应CS模型引入了遗忘因子、弱化因子以及截断概率等参数,使算法需要更多的先验信息。如果引入的参数不准确,就会使算法调节能力下降,导致环境的适应能力和鲁棒性降低。由于噪声的影响,滤波得到的参数和量测等信息相对于目标加速度的映射函数是非常复杂的,难以显式建模。神经网络对非线性函数的建模能力特别强,在许多领域均有广泛的应用和研究。而基于梯度反向传播训练方式的神经网络,训练时间长,调参过程复杂。
为了解决上述问题,本文将极限学习机(Extreme Learning Mechine,ELM)与CS 模型相结合,提出了基于极限学习修正的CS 模型跟踪算法(ELM-CS)。ELM 虽然结构简单,但学习训练速度极快,且非线性建模能力强,网络泛化能力好,因此得到了广泛的应用和发展。根据目标历史信息,使用ELM实时估计目标的加速度,ELM-CS通过实时修正加速度,使得算法能够更加准确估计加速度分布,提高了目标跟踪精度,且网络训练速度快,便于实际应用。
1 极限学习机
1 个典型的极限学习机是1 个单隐层前向神经网络。令该单层神经网络的节点数目为,则网络输出f,可以描述为:

这样得到的是ELM 的唯一解,因此,网络的泛化性较好。由于ELM 的神经元权值和偏置在训练之前已经随机赋值,故只计算,因此,ELM 的训练速度极快。
2 ELM-CS算法
目标的历史航迹可以在一定程度上反映目标趋势,而量测值以及轨迹滤波得到的归一化新息平方则可以在一定程度上反映目标的机动变化。因此,本文使用长度为的历史轨迹^、历史量测Z以及历史归一化信息平方e作为输入,通过ELM估计出当前时刻的加速度值:


图1 ELM-CS算法结构图Fig.1 Structure diagram of ELM-CS algorithm

3 ELM训练和机动目标跟踪测试
3.1 ELM网络训练

将训练集轨迹绘制,如图2所示。

图2 训练集轨迹Fig.2 Trajectories of training data set
有了训练集轨迹之后,需要使用CS 模型对目标轨迹进行跟踪滤波处理,以进一步得到训练集。数据集量测噪声为高斯白噪声,标准差为50 m。CS 模型滤波使用的过程噪声标准差为0.2 m,加速度极值为30 m/s,机动频率设置为1 20。采用的缓存时间窗口长度=10。由于轨迹数据的特点,其数据大小跟起点有关,因此,采用状态时间差值和量测时间差进行归一化,归一化方式为:

此时,ELM 输入的数据集的特征维度为9×(6+2+1)=81。对2 000 条训练集轨迹滤波并使用时间窗口获得训练集的规模为382 000条。
使用2层ELM。第1层为50个神经元,激活函数为sigmoid函数;第2层为20个神经元,激活函数为径向基函数。
使用python 版本的hpelm 1.0.10 工具箱完成ELM的构建和训练学习。训练结果,如表1所示。

表1 ELM训练结果Tab.1 ELM training results
因为输入输出均归一化,故训练精度和测试精度无单位,测试精度高于训练精度,是由于两者数据集规模相差1个数量级且轨迹有噪声造成的。
从表1 可以看到,ELM 训练速度极快,且泛化性好。
3.2 ELM-CS机动目标跟踪测试
为了充分分析ELM-CS 算法的性能,在2 种不同条件下对ELM-CS 进行机动目标跟踪性能测试,即通过测试集测试ELM-CS 的鲁棒性和泛化性,通过单条轨迹分析ELM-CS的跟踪优势。
根据3.1节数据集的生成规则,重新产生200条目标机动轨迹作为测试集。使用3.1节中相同设置下的ELM-CS 算法和标准CS 模型分别进行跟踪实验。由于轨迹各不相同,因此采用全局均方根误差(Global Root Mean Squared Error,GRMSE)作为衡量标准,定义如下:
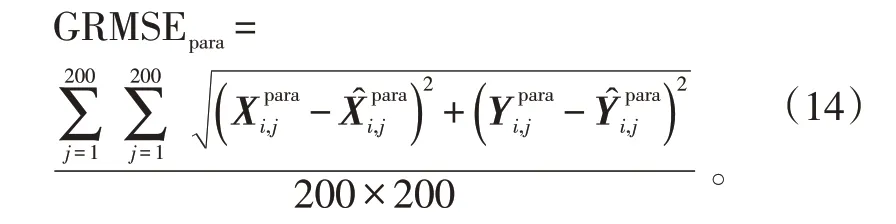
式(14)中:为跟踪步数;为轨迹序号;para 代表位置(p)、速度(v)以及加速度(a)维。
使用ELM-CS 算法以及CS 模型对测试集进行跟踪测试,得到测试结果,如表2所示。

表2 测试集跟踪结果Tab.2 Tracking results of test data set
从表2 可以看出,ELM-CS 算法较之标准CS 模型,在位置、速度、加速度的全局均方根误差均有显著降低,分别降低了约6 m、3.6 m/s 以及0.06 m/s,约降低了13.5%、13.6%以及0.8%。
从运行时间上看,虽然ELM-CS 跟踪200 条轨迹的运行时间是CS 模型的2 倍,但整体来说,增加的运算成本并不多,虽然使用了外部工具箱和其他数据处理工作,增加了运行时间,但实际上,从ELM的结构来看,真正的计算负担很小,是可以接受的。
本小节对单个轨迹进行跟踪测试,以进一步分析ELM-CS算法的性能。
从3.2.1小节中的测试集中随机抽选1条轨迹,进行200 次蒙特卡洛仿真测试。使用均方根误差(Root Mean Squared Error,RMSE),定义如下:
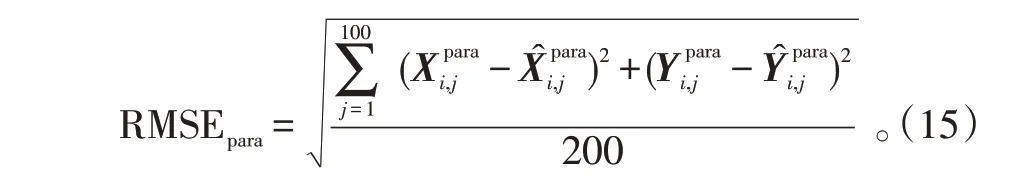
式(15)中,参数定义与式(14)一致。
通过蒙特卡洛仿真得到的位置和速度RMSE 对比,如图3和图4所示。
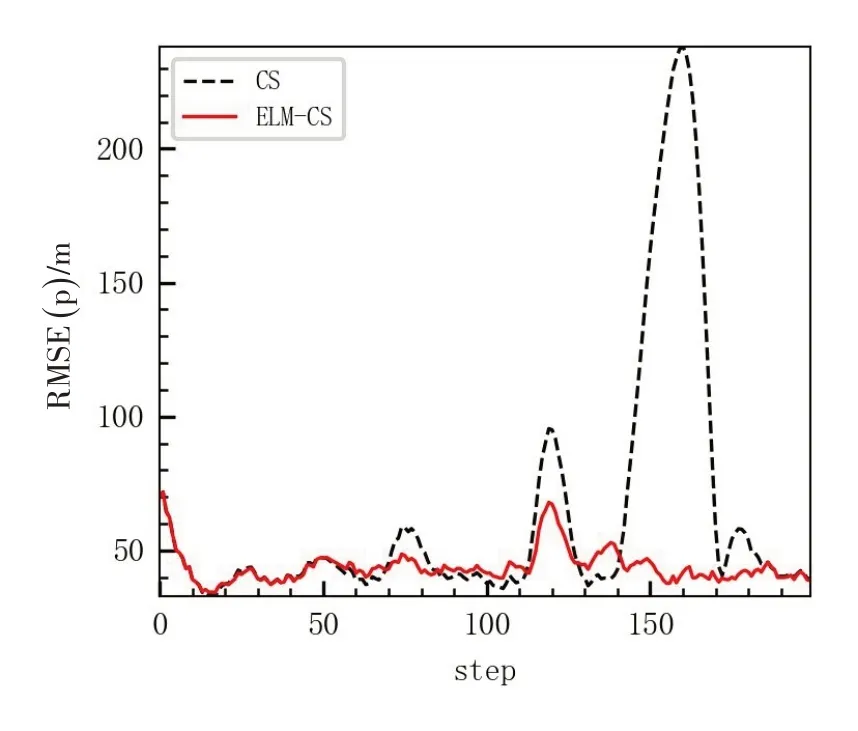
图3 位置RMSE对比图Fig.3 Comparison graph of RMSE values of position
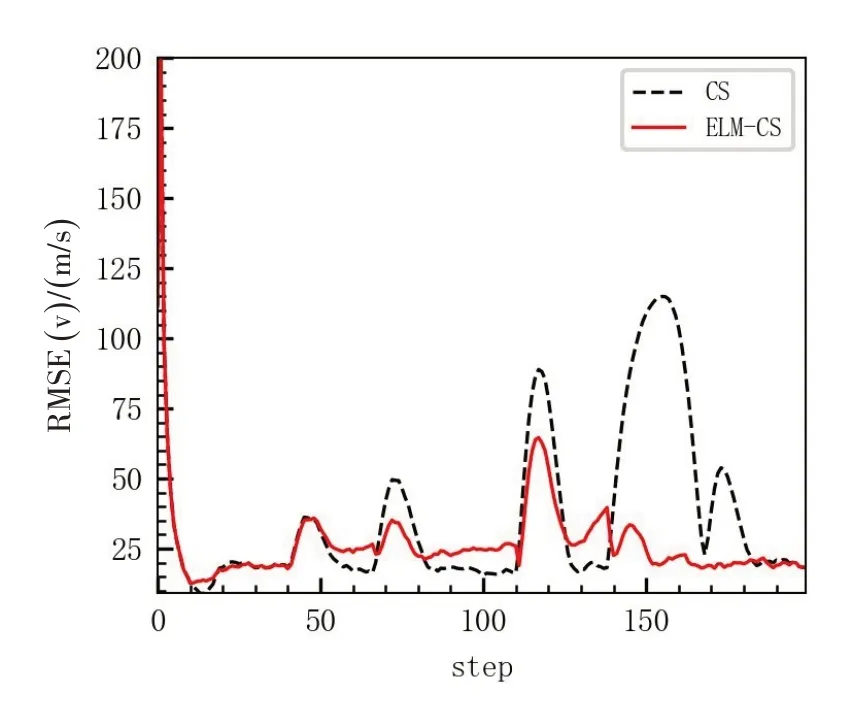
图4 速度RMSE对比图Fig.4 Comparison graph of RMSE values of velocity
将仿真得到的位置、速度以及加速度的RMSE的平均值(ARMSE)、峰值(PRMSE)对比,如表3 所示。由于滤波初期还未收敛,ARMSE以及PRMSE从第10跟踪步起算。

表3 蒙特卡洛仿真结果Tab.3 Monte-Carlo simulation results
从200次蒙特卡洛仿真中随机抽取1次仿真,将2个算法估计轨迹绘制,如图5所示。
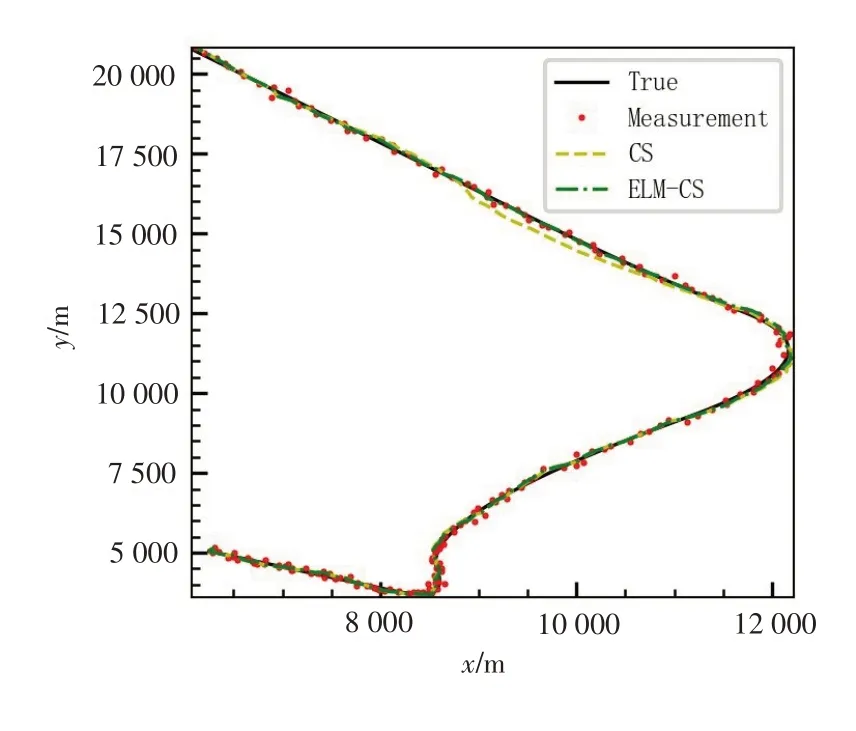
图5 跟踪轨迹对比图Fig.5 Comparison graph of tracking trajectories
由于本算法修正的是目标加速度估计,因此,将目标加速度估计对比,如图6所示。
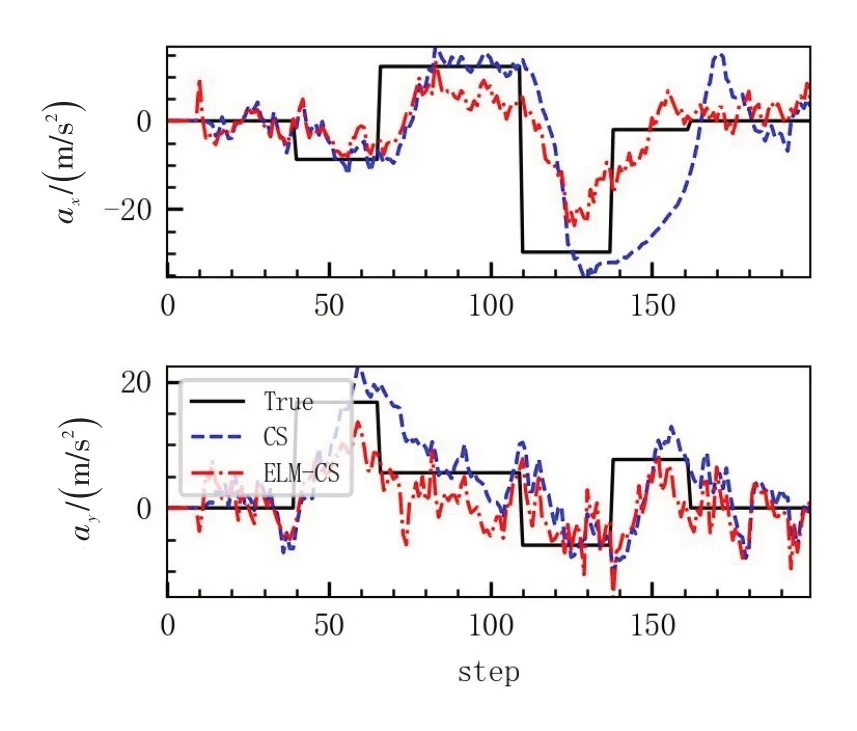
图6 加速度估计对比图Fig.6 Comparison graph of estimated values of acceleration
在目标跟踪中,由于机动目标的运动参数、模型等发生变化,且这些变化常常是突发且难以预测的,从图3、图4可以看出,在目标加速度发生变化也就是机动时,目标的跟踪RMSE 急剧增大,此时若是跟踪算法无法及时对机动做出正确估计和算法的调整,跟踪就可能发散。因此,机动目标是目标跟踪的重难点所在,机动阶段的自适应跟踪能力也是机动目标跟踪算法主要考察的方面。
从图3、图4 以及表3 可以看出,ELM-CS 算法较之标准CS模型,目标状态估计的位置、速度以及加速度的ARMSE以及PRMSE均有显著的提高,特别是位置、速度以及加速度的PRMSE 更是CS 模型的1/4 左右,说明ELM-CS在目标机动时,鲁棒性更强,可更快地切换机动参数,实现目标状态的正确估计。从图3的位置RMSE 更能发现,ELM 的加速度修正,使得ELM-CS算法全程以1种稳定的精度跟踪,而CS模型的跟踪精度却波动较大。
从图5和图6可以看出,ELM-CS算法较之标准的CS模型,其加速度由于通过ELM的修正和补偿,加速度估计波动更小,估计更为“保守”,这使得ELM-CS算法在面对机动时,能够具有更强的稳定性。
4 结束语
本文使用ELM根据目标的历史信息实时对CS模型的加速度估计进行修正和补偿,提出了ELM-CS。训练过程和仿真结果表明,该在测试集上,能够提高CS模型的位置和速度约14%的精度,在单轨迹的跟踪实验中,其位置、速度和加速度的ARMSE 和PRMSE均为CS 模型的1/4 左右,并且机动自适应性好,鲁棒性更强,加速度估计更为稳定。同时,ELM结构简单,训练速度极快,增加的计算成本很小,具有较好的实际应用价值。

