二叉树模型下欧式期权价值关于波动率的单调性研究

张会灵, 马飞遥

二叉树模型下欧式期权价值关于波动率的单调性研究

张会灵, 马飞遥*

（宁波大学 数学与统计学院, 浙江 宁波 315211）

研究了在市场无套利情况下, 二叉树模型的欧式期权价格与标的资产波动率的单调性问题. 首先给出了2个新的组合公式, 然后借助该组合公式证明了欧式期权价格与标的资产波动率存在单调递增关系.

二叉树模型; 期权定价; 波动率

期权作为一种金融衍生产品, 其定价是金融市场一个重要的研究领域. 近几十年来, 期权定价问题已得到广泛研究. Black等[1]提出了Black- Scholes期权定价模型, 虽然Black-Scholes期权定价模型有很多优点, 但其推导过程复杂. 随后Cox等[2]提出了一种简单的对离散时间期权的定价方法, 被称为C-R-R二项式期权定价模型. 近些年很多国内外学者在文献[2]基础上研究了二项式模型的期权定价问题[3-7]. 众所周知, 欧式期权的价格在C-R-R二项式期权定价模型中依赖于标的资产的波动性, 即欧式期权价格与标的资产波动率成单调递增关系. 近年来有关期权定价波动性的研究成果颇丰[8-10]. 陈怡[4]证明了在单期二叉树模型下欧式看涨期权关于波动率的单调关系, 但没有涉及多周期模型. Reynaerts等[11]通过对二叉树模型的期权定价进行敏感性分析, 得出了多周期时欧式看涨期权的价格不一定是波动率严格增加函数的结论, 但这种方法非常复杂.

本文利用2个新的组合公式, 更简便地证明了多周期二叉树模型下欧式期权价格与标的资产波动率的单调关系.

1 期权定价模型

对于欧式期权, 在支付红利情况下, 考虑形式为如下的欧式看涨期权定价公式[12]:

以及形式如下的欧式看跌期权定价公式[12]:

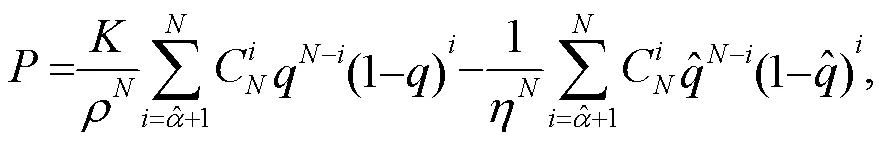
2 二叉树模型下欧式期权定价与波动率关系

给出2个新的组合公式, 这2个组合公式可应用于定理1的证明.

引理1

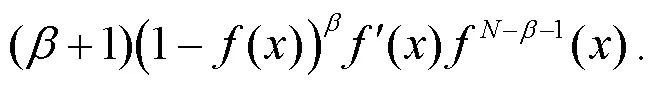
证明

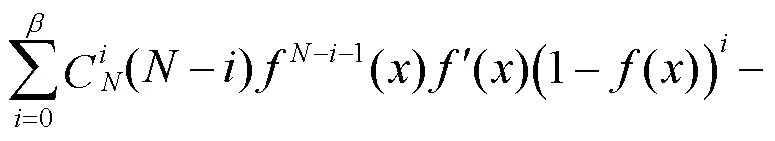
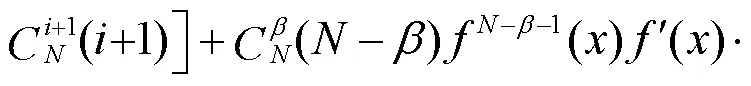
同理可证

引理1不仅可用于欧式期权价格关于波动率的单调性证明, 在其他研究中也有广泛应用.

式中:

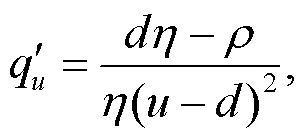
将式(6)代入式(5)整理可得:

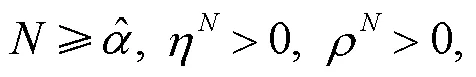
由于

可得:

若将欧式看涨期权定价式(1)对求偏导, 根据式(3)可得:

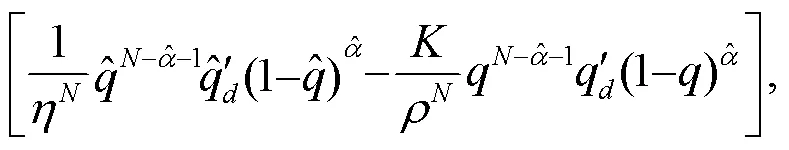
式中:

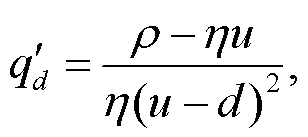
将式(10)代入式(9)整理可得:

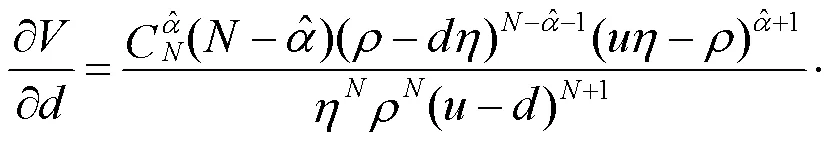
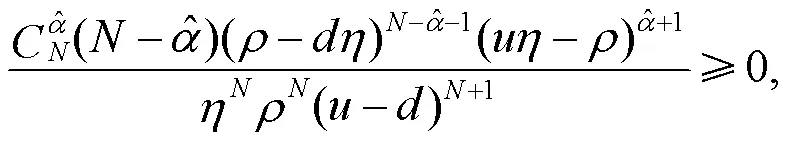
由于

可得:

那么由式(11)和式(12)可得:

式中:

将式(14)代入式(13)整理可得:

因为

所以

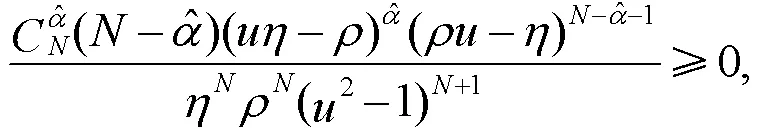
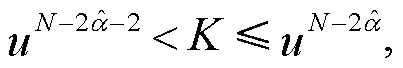
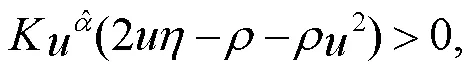
式中:

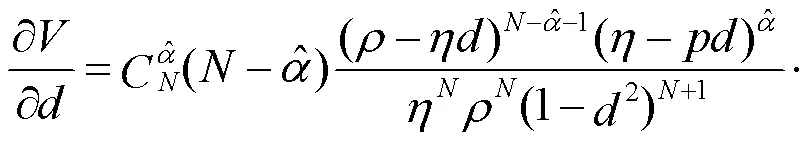
3 结语

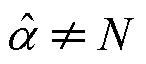
[1] Black F, Scholes M. The pricing of options and corporate liabilities[J]. Journal of Political Economy, 1973, 81(3): 637-654.

[2] Cox J C, Ross S A, Rubinstein M. Option pricing: A simplified approach[J]. Journal of Financial Economics, 1979, 7(3):229-263.

[3] Muzzioli S, Torricelli C. A multiperiod binomial model for pricing options in a vague world[J]. Journal of Economic Dynamics and Control, 2004, 28(5):861-887.

[4] 陈怡. 关于期权定价的模糊二叉树模型及其应用[D]. 天津: 天津大学, 2007.

[5] 陈怡. 关于欧式看涨期权的模糊二叉树模型[J]. 哈尔滨商业大学学报(社会科学版), 2007(6):10-12.

[6] 孔凡秋. 期权的二项式定价模型研究[J]. 经济研究导刊, 2014(4):134-135; 155.

[7] 冯晶晶, 樊亚云, 邢瑞芳. 二叉树从二期模型到n期模型的扩展[J]. 重庆理工大学学报(自然科学), 2016, 30(10):181-184.

[8] 国泰君安证券. 五大因素影响期权价格[N]. 证券时报, 2014-07-24(A15).

[9] 陈雨童. 基于波动率预测的期权定价研究[D]. 上海: 复旦大学, 2013.

[10] 龚谊洲. 基于可变波动率的期权定价研究[D]. 武汉: 华中师范大学, 2019.

[11] Reynaerts H, Vanmaele M. A sensitivity analysis for the pricing of European call options in a binary tree model [C]//Proceedings of the Third International Symposium on Imprecise Probabilities and Their Applications, 2003:14-17.

[12] 姜礼尚. 期权定价的数学模型和方法[M]. 2版. 北京: 高等教育出版社, 2008:24-39.

Monotonicity of volatility in European option pricing under binomial tree model

ZHANG Huiling, MA Feiyao*

( School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )

In this paper, we study the monotonicity of European option price and underlying asset volatility of the binary tree model for the case of no arbitrage. Firstly, we derive two new combination formulas. Then, based on these two combination formulas, the monotonic incrementing relation between European option pricing and underlying asset volatility is proved.

binary tree model; option pricing; volatility

F830.9

A

1001-5132（2022）03-0094-04

2021−03−23.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金（11971251）; 浙江省自然科学基金（LY20A010010）.

张会灵（1995－）, 女, 河南驻马店人, 在读硕士研究生, 主要研究方向: 偏微分方程. E-mail: 2764433623@qq.com

通信作者:马飞遥（1979－）, 男, 湖南衡阳人, 博士/副教授, 主要研究方向: 偏微分方程. E-mail: mafeiyao@nbu.edu.cn

（责任编辑 史小丽）